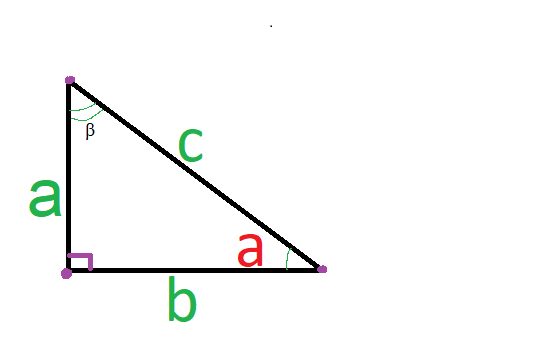Развернутый угол в геометрии
В этой статье будет рассматриваться одна из основных геометрических фигур – угол. После общего введения в это понятие мы уделим основное внимание отдельному виду такой фигуры. Развернутый угол – важное понятие геометрии, которое и будет основной темой этой статьи.
Введение в понятие геометрического угла
В геометрии существует ряд объектов, которые составляют основу всей науки. Угол как раз относиться к ним и определяется с помощью понятия луча, поэтому начнем именно с него.
Также перед тем, как приступать к определению самого угла, нужно вспомнить о нескольких не менее важных объектах в геометрии – это точка, прямая на плоскости и собственно сама плоскость. Прямой называют самую простую геометрическую фигуру, у которой нет ни начала, ни конца. Плоскостью – поверхность, которая имеет два измерения. Ну и луч (или же полупрямая) в геометрии – это часть прямой, у которой есть начало, но нет конца.
Используя данные понятия, можем составить утверждение, что углом является геометрическая фигура, которая полностью лежит в некоторой плоскости и состоит из двух несовпадающих лучей с общим началом. Такие лучи называются сторонами угла, а общее начало сторон – это его вершина.
Виды углов и геометрии
Мы знаем о том, что углы могут быть совсем разными. А потому немного ниже будет приведена небольшая классификация, которая поможет лучше разобраться в видах углов и их главных особенностях. Итак, существует несколько видов углов в геометрии:
- Прямой угол. Он характеризируется величиной в 90 градусов, а значит, его стороны всегда перпендикулярны между собой.
- Острый угол. К таким углам относятся все их представители, имеющие размер меньше 90 градусов.
- Тупой угол. Здесь же могут быть все углы с величиной от 90 до 180 градусов.
- Развернутый угол. Имеет размер строго 180 градусов и внешне его стороны составляют одну прямую.
Понятие развернутого угла
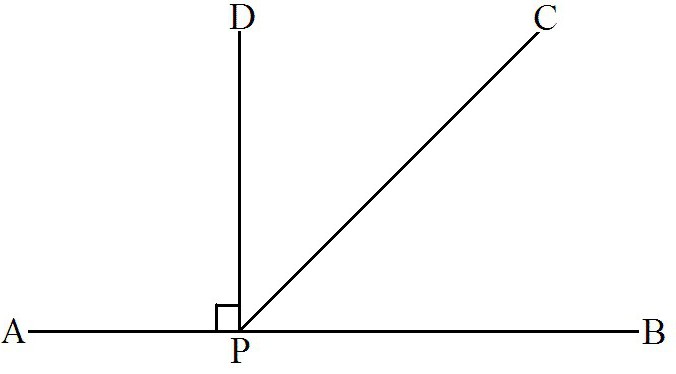
Теперь давайте рассмотрим развернутый угол более подробно. Это тот случай, когда обе стороны лежат на одной прямой, что можно четко увидеть на рисунке немного ниже. Значит, мы можем с уверенностью сказать, что у развернутого угла одна из его сторон по сути есть продолжением другой.
Стоит запомнить тот факт, что такой угол всегда можно разделить с помощью луча, который выходит из его вершины. В результате мы получим два угла, которые в геометрии называются смежными.
Также развернутый угол имеет несколько особенностей. Для того, чтобы рассказать о первой из них, нужно вспомнить понятие «биссектриса угла». Напомним, что это луч, который делит любой угол строго пополам. Что касается развернутого угла, то его биссектриса разделяет его таким образом, что образуется два прямых угла по 90 градусов. Это очень легко просчитать математически: 180˚ (градус развернутого угла) : 2 = 90˚.
Если же разделять развернутый угол совсем произвольным лучом, то в результате мы всегда получаем два угла, один из которых будет острым, а другой – тупым.
Свойства развернутых углов
Будет удобно рассматривать этот угол, собрав воедино все его главные свойства, что мы и сделали в данном списке:
- Стороны развернутого угла антипараллельны и составляют прямую.
- Величина развернутого угла всегда составляет 180˚.
- Два смежных угла вместе всегда составляют развернутый угол.
- Полный угол, который составляет 360˚, состоит из двух развернутых и равен их суме.
- Половина развернутого угла – это прямой угол.
Итак, зная все эти характеристики данного вида углов, мы можем использовать их для решения ряда геометрических задач.
Задачи с развернутыми углами
Для того, чтобы понять, усвоили ли вы понятие развернутого угла, попытайтесь ответить на несколько следующих вопросов.
- Чему равен развернутый угол, если его стороны составляют вертикальную прямую?
- Будут ли два угла смежными, если величина первого 72˚, а другого — 118˚?
- Если полный угол состоит из двух развернутых, то сколько в нем прямых углов?
- Развернутый угол разделили лучом на два таких угла, что их градусные меры относятся как 1:4. Вычислите полученные углы.
Решения и ответы:
- Как бы ни был расположен развернутый угол, он всегда по определению равен 180˚.
- Смежные углы имеют одну общую сторону. Поэтому, чтобы вычислить размер угла, который они составляю вместе, нужно просто прибавить значение их градусных мер. Значит, 72 +118 = 190. Но по определению развернутый угол составляет 180˚, а значит, два данных угла не могут быть смежными.
- Развернутый угол вмещает два прямых угла. А так как в полном имеется два развернутых, значит, прямых в нем будет 4.
- Если мы назовем искомые углы а и b, то пусть х — это коэффициент пропорциональности для них, а это значит, что а=х, и соответственно b=4х . Развернутый угол в градусах равен 180˚. И согласно своим свойствам, что градусная мера угла всегда равна сумме градусных мер тех углов, на которые он разбивается любым произвольным лучом, что проходит между его сторонами, можем сделать вывод, что х + 4х = 180˚, а значит, 5х = 180˚. Отсюда находим: х=а=36˚ и b = 4х = 144˚. Ответ: 36˚ и 144˚.
Если у вас получилось ответить на все эти вопросы без подсказок и не подглядывая в ответы, значит вы готовы переходить к следующему уроку по геометрии.
Что такое развернутый угол
В данной публикации мы рассмотрим, что такое развернутый угол, перечислим его основные свойства, а также разберем пример задачи по этой теме.
Определение развернутого угла
Угол является развернутым, если его градусная мера равняется 180 градусам.
Т.е. стороны угла образуют прямую.
Свойства развернутого угла
1. Луч, берущий начало в вершине развернутого угла, делит его на два угла, которые называются смежными.
2. Биссектриса развернутого угла делит его на два угла по 90° (т.е. прямых).
3. Если луч, который делит развернутый угол, не является его биссектрисой, то один из образованных углов меньше 90° (острый), а другой находится в промежутке от 90° до 180° (тупой).
Пример задачи
Дан развернутый угол, поделенный лучом на два угла, один из которых в три раза больше другого. Найдем градусные меры этих углов.
Решение
Пусть меньший угол будет “x” , тогда больший равен “3x” . Сумма этих углов равняется 180 градусам. Составим соответствующее уравнение и решим его:
Таким образом, первый угол равен 45°, а второй – 135° (45° умножаем на 3).
Проверка: 45° + 135° = 180° (верно).
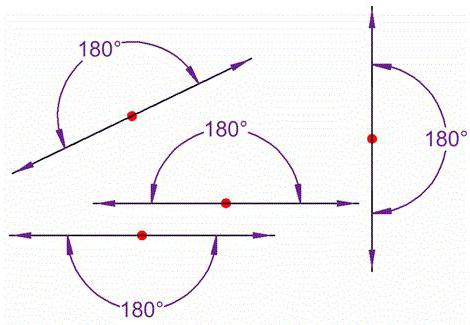
Развернутый угол
Развернутый угол — это угол, стороны которого лежат на одной прямой.
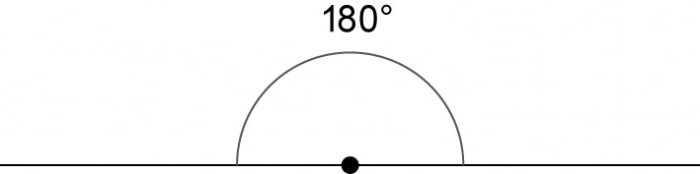
Градусная мера развёрнутого угла равна 180º.
Каждая сторона развернутого угла дополняет другую сторону до прямой, то есть стороны развёрнутого угла являются дополнительными лучами.
Например, ∠CDK — развёрнутый. Точка D — вершина, лучи DK и DC — стороны угла CDK.
Чтобы нарисовать развернутый угол, достаточно провести прямую и отметить на ней точку — вершину угла.
Можно поступить иначе — сначала отметить точку — вершину угла, затем через неё провести прямую:
∠AOB — развернутый угол
Если луч делит развернутый угол на два угла, то эти углы — смежные:
Например, ∠ABD — развернутый, BC — луч,
Биссектриса развернутого угла делит его на два прямых угла.
Например, KF — биссектриса развернутого угла MKP,
|
Для решения всех этих задачек надо помнить всего три правила:
Отсюда следует 1) угол В = 100 градусов 2) угол С = 70 градусов 3) угол А = 50 градусов 4) угол В = 60 градусов 5) угол А = 40 градусов 6) угол В = 35 градусов, тут вступает еще и лемма, что противоположные углы равны меж собой 7) угол В = 40 градусов 9) угол В = 70 градусов. Скукота, однако (не названные мной углы посчитайте сами, вам понравится!) Знаете ответ? |
Что такое развёрнутый угол — понятие и обозначение
Определение
Развернутым называют угол со сторонами, лежащей на одной прямой.
Стороны развернутого угла взаимно дополняют друг друга. В результате получается прямая линия. Таким образом, стороны данной геометрической фигуры представляют собой дополнительные лучи. К примеру, на рисунке изображен ∠CDK, который является развернутым. Точка D служит его вершиной, лучи, обозначенные, как DK и DC – сторонами ∠CDK.
Решить задачу, в которой требуется начертить развернутый угол достаточно просто. Необходимо нарисовать прямую линию и поставить на ней отметку в виде точки, которая будет являться вершиной. Существует другой способ. В начале на плоскости отмечают произвольную точку. Данная отметка будет принята за вершину угла. Если через нее прочертить прямую линию, то получится развернутый угол. Схематично оба способа представлены на рисунке.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Определить, является ли угол развернутым, тупым или острым можно с помощью ряда признаков.
Основные свойства развернутого угла:
- Стороны геометрической фигуры являются антипараллельными и складываются в прямую линию.
- Развернутый угол в любом случае, независимо от способа начертания, будет составлять 180 градусов.
- Если соединить вместе пару смежных углов, то полученная фигура будет выглядеть, как развернутый угол.
- В случае, когда соединяют пару развернутых углов, в результате получают полный угол в 360 градусов, который равен сумме этих углов.
- Прямой угол является половиной развернутого угла.
Геометрические фигуры с развернутыми углами
В геометрии производя некоторые манипуляции с развернутыми углами, можно получить новые фигуры. К примеру, если такую геометрическую фигуру разделить лучом на два угла, то полученные углы называют смежными. Такие элементы изображены на рисунке.
∠ABD в данном случае является развернутым углом, а ВС представляет собой луч. Таким образом, углы ∠ABС и ∠CBD — смежные углы.
С помощью биссектрисы можно разделить представленную фигуру на два прямых угла. Наглядно данный метод получения геометрических фигур продемонстрирован на рисунке.
Так, согласно изображению, KF является биссектрисой развернутого ∠MKP. Полученные углы, ∠MKF и ∠FKP представляют собой прямые углы.
Какова градусная мера развернутого угла (сколько радиан)
Как и любой другой, развернутый угол можно измерить. Градусная величина геометрической фигуры будет составлять (180^{0}). Известно, что в данной единице меры укладывается 3,1415926… радиан. Так как длинные числа не всегда удобно использовать в расчетах, как правило, это число обозначают буквой π. Таким образом, можно записать следующее справедливое обозначение:
(180^{0}approx 3,14) радиан.
Точное отношение будет иметь следующий вид:
(180^{0}=pi) радиан.
Примеры решения задач с развернутыми углами
Задача №1
Развернутый угол разделили с помощью луча на две части, которые являются аналогичными геометрическими фигурами. Градусные меры этих элементов относятся, как 1:4. Требуется найти полученные углы.
Решение
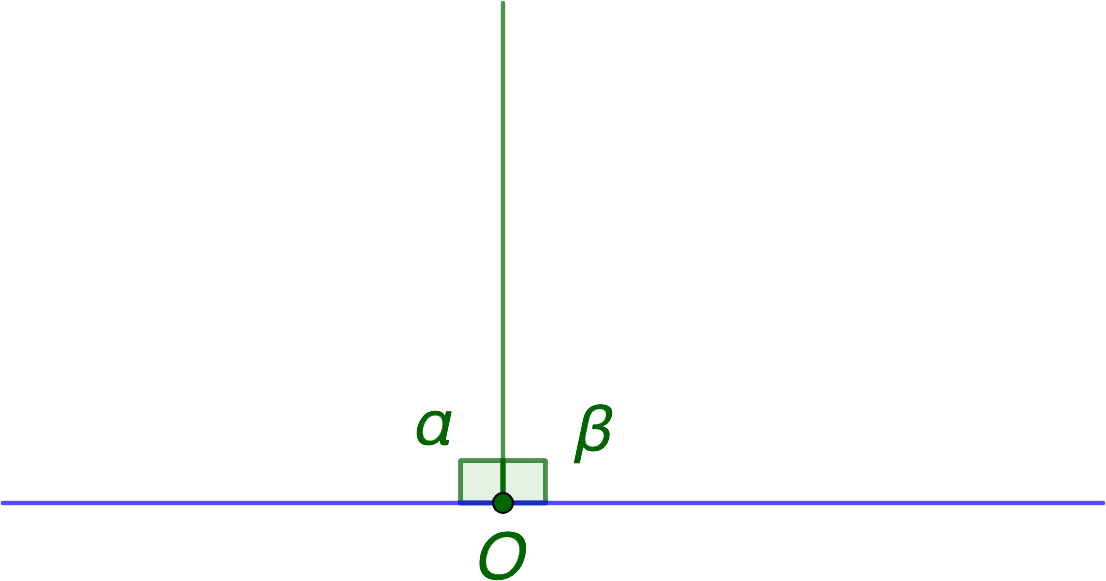
Следует обозначить искомые фигуры, как α и β. Предположим, что х является коэффициентом пропорциональности, тогда справедливы равенства:
α = х
β = 4х
Зная, что развернутый угол равен 180 градусам, что является суммой градусных мер углов, на которые он разбит с помощью луча, проходящего между его сторонами. Данное утверждение вытекает из свойств этой геометрической фигуры. Можно записать следующую формулу:
(x+4x=180^{0}Rightarrow 5x=180^{0})
Исходя из этого, можно определить углы:
(x=alpha =36^{0})
(beta =4x=4*36^{0}=144^{0})
Ответ: после разделения развернутого угла на две части один угол будет равен (36^{0}) второй ставит (144^{0})
Задача 2
С помощью луча ОС развернутый угол, обозначенный, как АОВ, делят на два угла АОС и ВОС таким образом, что градусная мера угла АОС больше на 30 градусов, чем градусная мера угла ВОС. Требуется найти углы АОС и ВОС.
Решение
Условия задачи следует представить на рисунке:
Допустим, что ∠BOC = x, тогда, согласно условию задачи, получим следующее равенство:
∠AOC=(x+30)
Известно, что образованные углы являются смежными. Таким образом, в сумме эти углы будут составлять (180^{0})
∠AOC+∠BOC=180
В результате уравнение приобретает следующий вид:
(x+x+30=180Rightarrow 2x=150Rightarrow x^{0}=75^{0})
∠BOC=75, откуда следует:
∠AOC=(x+30)=105
Ответ: угол (BOC=75^{0}) угол (AOC=105^{0})
Треугольник – это форма многоугольника, которая имеет три угла, образованных тремя сторонами. Каждая
из трех точек, в которых пересекаются стороны треугольника, называется его вершиной и образует
определенный угол. Стороны треугольника иногда еще называют линейными длинами, а углы – угловыми.
Сторону, противоположную определенному углу, обозначают той же буквой, что характеризует угол как
прилегающий. Стороны обозначаются латинскими буквами a, b, c, а углы – греческими α, β, γ. Зная
определенные параметры треугольника, можно найти его стороны и углы. При этом можно использовать как
линейные формулы, так и обращаться к различным теоремам, например, теореме синусов и косинусов.
- Угол треугольника через три стороны
- Угол прямоугольного треугольника через две стороны
- Угол треугольника через высоту и катет
- Угол при основании равнобедренного треугольника через
биссектрису и боковую сторону - Угол при основании равнобедренного треугольника через
биссектрису и основание - Угол между боковыми сторонами равнобедренного треугольника
через биссектрису и боковую сторону - Острый угол прямоугольного треугольника через катет и
площадь - Острый угол между боковыми сторонами равнобедренного
треугольника через площадь и боковую сторону
Угол треугольника через три стороны
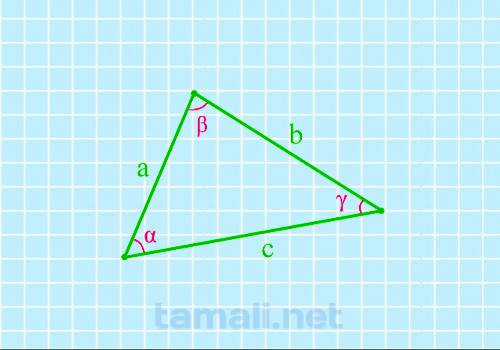
Для того, чтобы найти угол по трем сторонам, нужно вычислить косинус определенного угла. Согласно
теореме косинусов, «квадрат длины стороны треугольника равен сумме квадратов двух других длин его
сторон, минус удвоенное произведение этих длин сторон на косинус угла между ними». Если взять за
предмет вычисления угол β, соответственно, получаем формулу: a² = b² + c² — 2 · b · c · cos (β).
Из полученного равенства можно вычислить
cos(α) = (a² + c² — b²) / 2ac
cos(β) = (a² + b² — c²) /
2ab
cos(γ) = (b² + c² — a²) / 2cb
где a, b, c — стороны треугольника.
Цифр после
запятой:
Результат в:
Пример. Пусть a = 3, b = 7, c = 6. Cos (β) = (7² + 6² — 3²) : (2 · 7 · 6) = 19/21.
Зная косинус, нужно воспользоваться таблицей Брадиса и по ней найти угол. По таблице Брадиса, если
Cos (β) = 19/21, то β = 58,4°.
Угол прямоугольного треугольника через две стороны
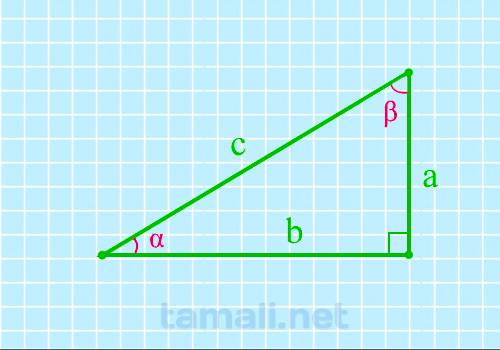
Если известен катет и гипотенуза, угол вычисляется через синус. Если известны катеты и нужно найти
один из острых углов, то можно сделать это через вычисление тангенса.
sin(α) = cos (β) = a / c
sin(β) = cos (α) = b / c
tg(α) = ctg(β) = a
/ b
tg(β) = ctg(α) = b / a
где a, b — катеты, c — гипотенуза.
Цифр после запятой:
Результат в:
Пример. В прямоугольном треугольнике есть два катета a = 12, b = 9 и гипотенуза c =
15. Если известны катеты и нужно найти один из острых углов, то можно сделать это через вычисление
тангенса: tg(α) = a / b, то есть tg(α) = 12 / 9. По таблице Брадиса, угол
α = 53, 13°. Если известен катет и гипотенуза, угол вычисляется через синус sin(α) = a / c = 12 / 15 = 0,8. В
этом случае по таблице Брадиса для синусов и косинусов, значение угла – 36, 87°.
Острый угол прямоугольного треугольника через катет и площадь
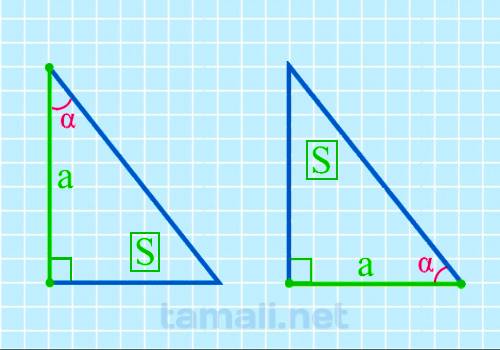
Для того, чтобы вычислить размер острого угла, нужно образовать обратную формулу от площади
прямоугольного треугольника, которая вычисляется через катет и острый угол. Выглядит она следующим
образом: S = (a² * tg β) / 2. Из этих показателей известный площадь S и катет a. Отсюда формула для
нахождения угла будет следующая:
tg(α) = a² / 2S
где a — катет, S — площадь прямоугольного треугольника.
Цифр после
запятой:
Результат в:
Пример. Пусть S = 34, a = 8. Получается следующее уравнение: tg(α) = a² / 2S = 8² + 2 * 34 = 132.
Таким образом выходит, что по таблице Брадиса, угол с таким тангенсом равен 43°.
Угол треугольника через высоту и катет
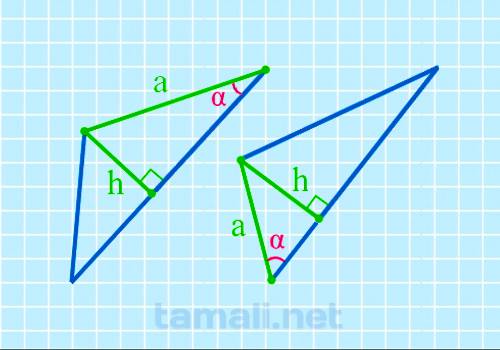
В некоторых прямоугольных треугольниках, в основании которых один острый угол, а второй 90°, один из
катетов (вертикальная прямая, образующая прямой угол) называется также высотой и обозначается как h.
Второй катет a остается со своим обычным названием.
sin α = h / a
где h — высота, a — катет.
Цифр после запятой:
Результат в:
Пример. Если высота h = 8, а катет a = 10, то угол α находится по формуле sin α = h / a = 8 / 10 = 0.8 то по таблице Брадиса составляет 53°
Угол при основании равнобедренного треугольника через биссектрису и основание
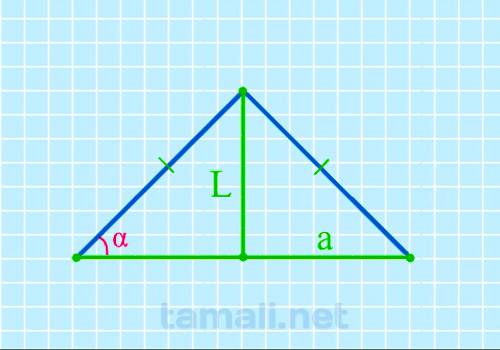
Равнобедренный треугольник ABC с основанием AC имеет биссектрису L (она же CK, делящая основание AC
на два отрезка AK и KB). Также биссектриса L делит угол BCA (он же γ) пополам (каждый из этих
половинок угла γ обозначается как x). То есть γ = 2х. Угол BAC (он же α) = BCA (он же γ), то есть α
= γ. При этом биссектриса L (она же CK) образовала в равнобедренном треугольнике ABC новый
равнобедренный треугольник AKC, в котором AK – это основание, а углы KAC и AKC равны между собой и
равны значению угла γ. Учитывая то, что угол γ равен 2х (то есть двум половинкам угла), то для
треугольника AKC, чтобы вычислить углы при основании, формула будет следующая:
tg α = L / (a/2)
где L — биссектриса, a — основание.
Цифр после
запятой:
Результат в:
Пример. Пусть биссектриса L равна 15, основание а равно 45, подставив в формулу
получим tg α = L / (a/2) = 15 / (45/2) = 33.69º
Угол при основании равнобедренного треугольника через биссектрису и боковую сторону
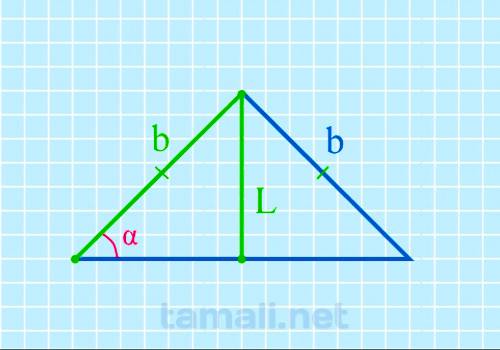
Допустим, что у равнобедренного треугольника ABC углы при основании A (α) и C (γ) равны. Также AB =
BC. Биссектриса L берет начало из вершины А и пересекается с основанием АС, образуя точку
пересечения K, поэтому биссектрису L также можно называть АK. L разделила угол А пополам и основание
поделила на два отрезка: BK и KC. Образовался угол AKC = α (внешний угол для треугольника ABK).
Согласно свойствам внешнего угла:
sin α = L / b
где L — биссектриса, b — боковая сторона.
Цифр после
запятой:
Результат в:
Пример. Пусть биссектриса L равна 15, боковая сторона b равна 30, подставив в
формулу получим sin α = L / b = 15/30 = 30º.
Угол между боковыми сторонами равнобедренного треугольника через биссектрису и боковую сторону
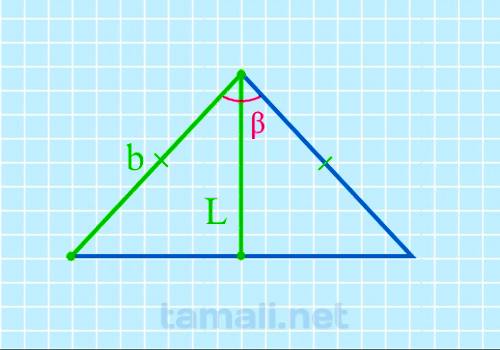
В равнобедренном треугольнике угол ABC (он же β) – это вершина треугольника. Стороны AB и BC равны, и
углы у основания BAC (α) и BCA (γ) тоже равны между собой. Биссектриса L берет начало из вершины B и
пересекается с основанием AC в точке K. Биссектриса BK разделила угол β пополам. Кроме того,
биссектриса разделила треугольник ABC на два прямоугольных треугольника ABK и CBK, так как углы BKA
и BKC – прямые и оба по 90°. Так как треугольники ABK и CBK зеркально одинаковые, для определения
угла β можно взять любой из них. В свою очередь биссектриса BK разделила угол β пополам, например,
на два равных угла х. Оба треугольника, образовавшихся внутри равнобедренного из-за биссектрисы,
прямоугольные, поэтому, чтобы вычислить угол β (он же 2х), нужно взять за правило вычисление угла
через высоту (она в данном случая является также биссектрисой) и катет (это отрезок AK или KC,
которые также равны между собой, так как биссектриса и основание равнобедренного треугольника также
поделила пополам).
2cos(β) = L / b
где L — биссектриса, b — боковая сторона.
Цифр после
запятой:
Результат в:
Пример. В треугольнике BKC известна биссектриса L = 47 см и боковая сторона b = 64
см. Подставив значения в формулу получим: 2cos(β) = L / b = 47 / 64 = 85.49º
Острый угол между боковыми сторонами равнобедренного треугольника через площадь и боковую
сторону
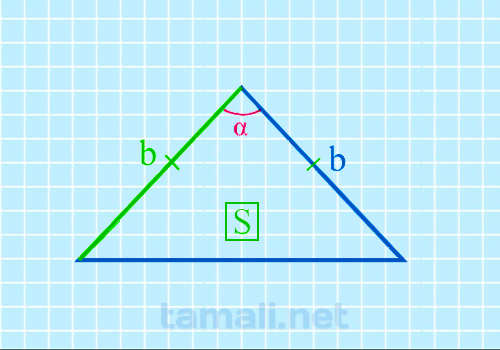
Формула площади равнобедренного треугольника S = 1/2 * bh, где b – это
основание треугольника, а h – это медиана, которая разделила равнобедренный треугольника на два
прямоугольных. Формула для нахождения угла между боковыми сторонами через площадь и боковую сторону
будет следующая:
sin(α) = 2S / b²
где b — боковая сторона равнобедренного треугольника, S — площадь.
Цифр после
запятой:
Результат в:
Пример. Если площадь равна 48, а сторона 10, то угол между боковыми сторонами можно
вычислить следующим образом: sin(α) = 2S / b² = 2 * 48 / 10² = 73.7º
Вне зависимости от условия задачи, известно, что сумма всех углов треугольника составляет 180°.
Поэтому, элементарно вычислить один из углов можно, когда известны два других. Но для вычисления
углов могут быть использованы и другие показатели. Например, для того, чтобы находить стороны и углы
треугольников, в них можно проводить дополнительные меридианы, биссектрисы, чертить окружности и
использовать эти фигуры как дополнительные вводные, через которые по формулам находятся
неизвестные.
Углы очень удобно вычислять через синусы, косинусы, тангенсы и котангенсы, после чего сопоставлять
данные с таблицей Брадиса, в которой эти величины можно сконвертировать в градусы.
При рассмотрении основных составляющих измерения углов, следует изучить исходные геометрические сведения:
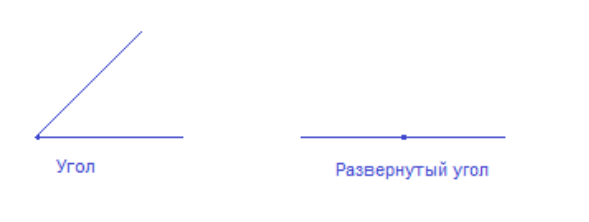
- Угол.
- Развернутый угол, неразвернутый угол.
- Градус, секунда и минута.
- Градусная мера.
- Острый, прямой или тупой.
Геометрическая фигура, которая представляет собой точку — называется вершиной. А исходящие из этой вершины два луча, являются ее сторонами.
Измерение углов производится с помощью градусной меры угла. Углы измеряются таким же способом, как и отрезки, при помощи специальных единиц измерения – градусов.
Определение
Градус — геометрическая единица измерения, представляющая собой угол, который сравнивается с другими углами.
Равенство градуса таково: [frac{1}{180}] от развернутого угла. Исходя из этого, можно понять, что развернутый угол равен 180 градусам, а неразвернутый угол любой меньше 180 градусов.
Чему равна градусная мера угла
Определение
Градусная мера угла – это положительное число, которое показывает сколько раз градус и его части укладываются в данном углу.
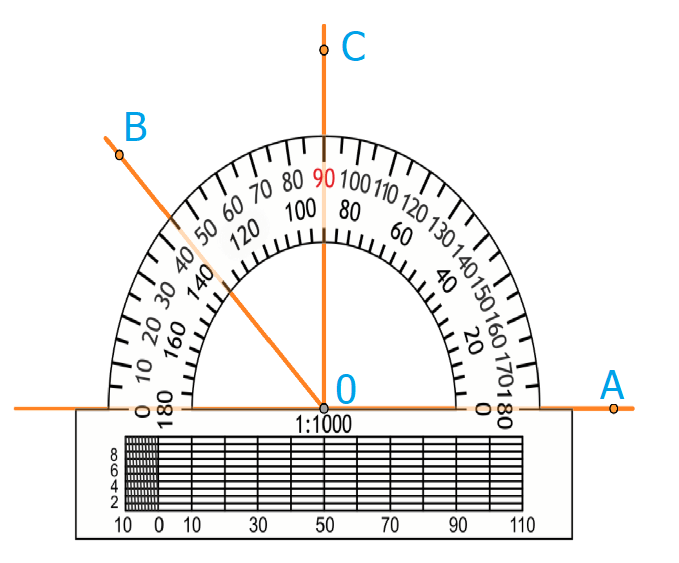
А для их измерения используется инструмент – транспортир.
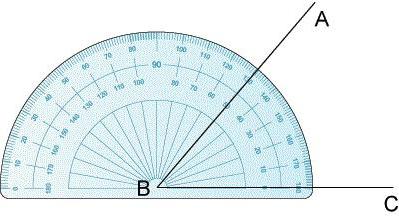
Транспортир используется следующим образом:
- Совместить вершину угла с центром транспортира, при этом одна сторона угла должна пройти по линейке.
- Штрих на шкале транспортира, через который пройдет 2-я сторона, покажет его градусную меру.
Как найти градусную меру угла
На рисунке угол АОВ = 135 градусов. Угол АОС = 90 градусов, угол ВОС = 45 градусов. Градусная мера углов равна сумме углов, на которые он разбит лучом, который проходит между его сторонами.
Отсюда следует, что величина угла AOB на рисунке 1 равна сумме величин углов AOC и [B O C: angle A O B=angle A O C+angle B O C].
Какие бывают названия углов можно понять, разобравшись со следующими обозначениями.
- Минута – 1/60 часть градуса. Обозначается знаком ‘
- Секунда – 1/60 часть минуты. Обозначают знаком»
Например: угол в 65 градусов, 35 минут,18 секунд записывается так: 75°45’28». Если градусная мера у нескольких углов одинаковая, эти углы считаются равными. Сравнить их можно по размерам – больше или меньше. Развернутый и неразвернутый углы.
Нет времени решать самому?
Наши эксперты помогут!
Градусная мера вписанного угла
Градусная мера вписанного угла равняется половине градусной меры дуги, опирающуюся на нее, и половине градусной меры угла, находящегося по центру, которая опирается на эту же дугу.
Вписанный угол равняется половине градусной меры дуги, на которую он опирается.
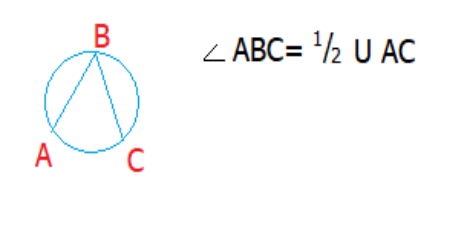
АВ-хорда
ВС-хорда
В-точка окружности.
Углы также различаются несколькими типами:
- Прямыми
- Острыми
- Тупыми
Равность прямого угла составляет — 90 градусов. Острый равен цифре меньше 90 градусов. А тупой же – больше 90 и меньше 180 градусов. В чем же заключается важность умения измерения углов и градусной меры в жизни? Оно пригодится в исследованиях, таких как: астрономия. Например, чтобы вычислить положение различных тел в космосе. Чтобы попрактиковаться, необходимо прочертить несколько неразвернутых углов, отличающихся друг от друга. Также важно потренироваться чертить развернутые. А еще, можно при помощи транспортира поупражняться, задавая случайные цифры, в правильности воспроизведения углов.
Существует еще такое понятие, как, биссектриса.
Определение
Биссектриса— луч, который исходит из вершины этого угла и делит его пополам.
Пример 1. Задача с биссектрисой и развернутым углом.
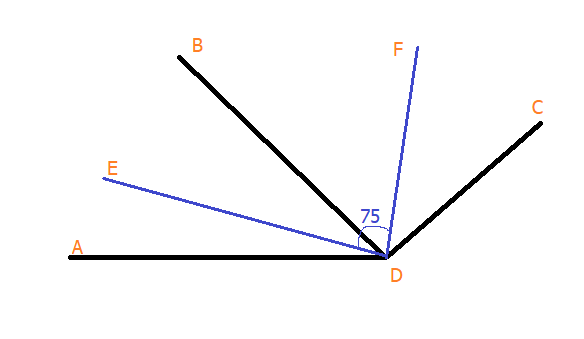
Рис.3 Лучи DЕ и DF – это биссектрисы, которые соответствуют углам ADB и BDC.
Теперь нужно найти угол ADC, при этом угол EDF = 75°
Ответ. Угол EDF имеет по половинке от углов ADB и BDC, это значит, что EDF – это половина самого угла ADC. Теперь получили вычисление угол ADC = 75 умножить на 2 = 150°.
Ответ: 150°
Пример 2. Задача с биссектрисой и прямым углом.
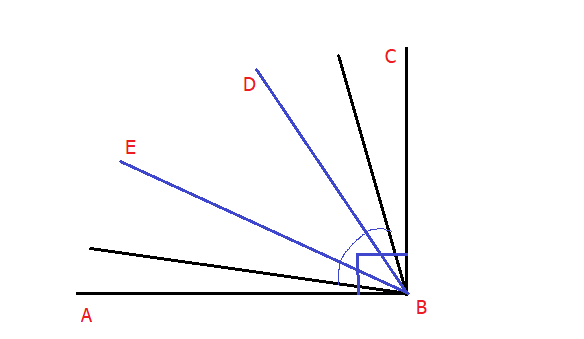
Рисунок 4. По рисунку 4 видно, что угол АВС прямой, а углы ABE EBD DBC равны. Нужно найти угол, который образовали биссектрисы — ABE и DBC.
Решение будет таким: угол АВС прямой, и исходя из этого, можно понять что он равен 90°. Угол ЕВD=90/3=30°. Согласно правилу, углы ABE EBD DBC равны и поэтому каждый из них будет = 30°. Далее видно, что биссектриса любого из трех углов делит любой из этих углов на 2 угла, которые будут равны 15°. Обе половины углов ABE и DBC относятся к углу, который необходимо найти, то можно смело утверждать, что угол, который мы вычисляем, равен 30+15+15=60°.
Решение: 60°
Градусная мера углов треугольника
У любой геометрической фигуры, кроме округлой, имеются углы. При рассмотрении углов треугольника можно увидеть следующее: Сумма углов треугольника всегда равняется 180°. Если рассматривать прямоугольный треугольник, то можно увидеть, что один из углов равен 90°. А сумма двух других углов тоже равняется 90°.
Поэтому, если известно сколько градусов составляет один из острых углов треугольника, второй угол можно найти по формуле:
[angle a=90^{circ}-angle beta]
У прямоугольного треугольника один из углов прямой, соответственно, два других – острые.
Разъяснение острого угла таково: острым углом называется угол, значение которого составляет менее 90 градусов.
Исходя из вышесказанного, можно отметить, что прямоугольный треугольник — это геометрическая фигура, которая образовалась из трех отрезков. Эти отрезки соединяются между собой тремя точками. Углы у нее все внутренние, а один из них — прямой и равняется 90°. Пример — рисунок 5.




 углы А и С — по 65,5 градуса
углы А и С — по 65,5 градуса