Что такое развёрнутый угол — понятие и обозначение
Определение
Развернутым называют угол со сторонами, лежащей на одной прямой.
Стороны развернутого угла взаимно дополняют друг друга. В результате получается прямая линия. Таким образом, стороны данной геометрической фигуры представляют собой дополнительные лучи. К примеру, на рисунке изображен ∠CDK, который является развернутым. Точка D служит его вершиной, лучи, обозначенные, как DK и DC – сторонами ∠CDK.
Решить задачу, в которой требуется начертить развернутый угол достаточно просто. Необходимо нарисовать прямую линию и поставить на ней отметку в виде точки, которая будет являться вершиной. Существует другой способ. В начале на плоскости отмечают произвольную точку. Данная отметка будет принята за вершину угла. Если через нее прочертить прямую линию, то получится развернутый угол. Схематично оба способа представлены на рисунке.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Определить, является ли угол развернутым, тупым или острым можно с помощью ряда признаков.
Основные свойства развернутого угла:
- Стороны геометрической фигуры являются антипараллельными и складываются в прямую линию.
- Развернутый угол в любом случае, независимо от способа начертания, будет составлять 180 градусов.
- Если соединить вместе пару смежных углов, то полученная фигура будет выглядеть, как развернутый угол.
- В случае, когда соединяют пару развернутых углов, в результате получают полный угол в 360 градусов, который равен сумме этих углов.
- Прямой угол является половиной развернутого угла.
Геометрические фигуры с развернутыми углами
В геометрии производя некоторые манипуляции с развернутыми углами, можно получить новые фигуры. К примеру, если такую геометрическую фигуру разделить лучом на два угла, то полученные углы называют смежными. Такие элементы изображены на рисунке.
∠ABD в данном случае является развернутым углом, а ВС представляет собой луч. Таким образом, углы ∠ABС и ∠CBD — смежные углы.
С помощью биссектрисы можно разделить представленную фигуру на два прямых угла. Наглядно данный метод получения геометрических фигур продемонстрирован на рисунке.
Так, согласно изображению, KF является биссектрисой развернутого ∠MKP. Полученные углы, ∠MKF и ∠FKP представляют собой прямые углы.
Какова градусная мера развернутого угла (сколько радиан)
Как и любой другой, развернутый угол можно измерить. Градусная величина геометрической фигуры будет составлять (180^{0}). Известно, что в данной единице меры укладывается 3,1415926… радиан. Так как длинные числа не всегда удобно использовать в расчетах, как правило, это число обозначают буквой π. Таким образом, можно записать следующее справедливое обозначение:
(180^{0}approx 3,14) радиан.
Точное отношение будет иметь следующий вид:
(180^{0}=pi) радиан.
Примеры решения задач с развернутыми углами
Задача №1
Развернутый угол разделили с помощью луча на две части, которые являются аналогичными геометрическими фигурами. Градусные меры этих элементов относятся, как 1:4. Требуется найти полученные углы.
Решение
Следует обозначить искомые фигуры, как α и β. Предположим, что х является коэффициентом пропорциональности, тогда справедливы равенства:
α = х
β = 4х
Зная, что развернутый угол равен 180 градусам, что является суммой градусных мер углов, на которые он разбит с помощью луча, проходящего между его сторонами. Данное утверждение вытекает из свойств этой геометрической фигуры. Можно записать следующую формулу:
(x+4x=180^{0}Rightarrow 5x=180^{0})
Исходя из этого, можно определить углы:
(x=alpha =36^{0})
(beta =4x=4*36^{0}=144^{0})
Ответ: после разделения развернутого угла на две части один угол будет равен (36^{0}) второй ставит (144^{0})
Задача 2
С помощью луча ОС развернутый угол, обозначенный, как АОВ, делят на два угла АОС и ВОС таким образом, что градусная мера угла АОС больше на 30 градусов, чем градусная мера угла ВОС. Требуется найти углы АОС и ВОС.
Решение
Условия задачи следует представить на рисунке:
Допустим, что ∠BOC = x, тогда, согласно условию задачи, получим следующее равенство:
∠AOC=(x+30)
Известно, что образованные углы являются смежными. Таким образом, в сумме эти углы будут составлять (180^{0})
∠AOC+∠BOC=180
В результате уравнение приобретает следующий вид:
(x+x+30=180Rightarrow 2x=150Rightarrow x^{0}=75^{0})
∠BOC=75, откуда следует:
∠AOC=(x+30)=105
Ответ: угол (BOC=75^{0}) угол (AOC=105^{0})
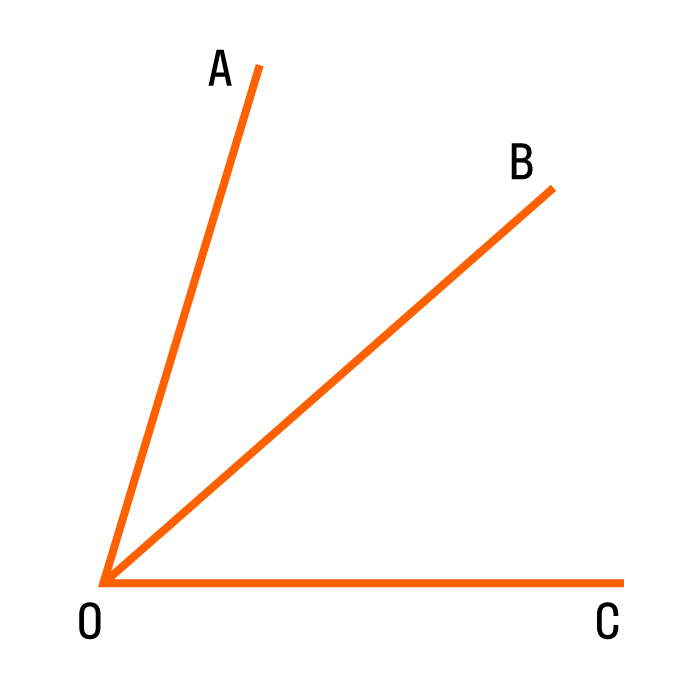
Геометрическая фигура угол образуется из двух лучей с общей начальной точкой.
Общая точка называется вершиной угла, а лучи — сторонами угла.
Для названия угла часто используют три большие латинские буквы, название вершины угла пишется посередине.
Иногда угол можно назвать только одной буквой, которая находится у вершины.
Можно также познакомиться с греческим алфавитом и использовать маленькие буквы для названий углов.
Чаще используют:
α,β,γ,δ,ϵ,η,ϕ,ω
— и другие.
Попытаемся представить точку как что-то бесконечно маленькое, а прямую — как что-то бесконечно простирающееся в обе стороны.
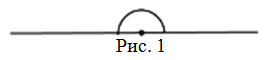
Рис. (1). Угол
∡ABC
,
∡B
или
∡α
.
Если угол образован дополнительными (или противоположными) лучами, то он называется развёрнутым.
Рис. (2). Развёрнутый угол
∡KLM
.
Так же как каждый отрезок имеет длину, которую можно измерить линейкой и выразить в единицах измерения, так и каждый угол имеет величину.
За единицу измерения углов принимают градус, что является
1180
частью развёрнутого угла.
Величина развёрнутого угла — (180°).
Углы измеряют транспортиром.
Рис. (3). Транспортир.
Особый угол, половина развёрнутого угла — прямой угол.
Прямой угол обозначают маленьким квадратиком внутри угла.
Величина прямого угла равна (90°).

Рис. (4). Прямой угол.
Углы, величина которых меньше (90°), называются острыми.
Углы, величина которых больше (90°), называются тупыми.
Источники:
Рис. 1. Угол, © ЯКласс.
Рис. 2. Развёрнутый угол, © ЯКласс.
Рис. 3. Транспортир. © ЯКласс.
Рис. 4. Прямой угол, © ЯКласс.
Математика
Тема 8: Инструменты для вычислений и измерений
Урок 2: Угол. Прямой и развернутый угол. Чертежный треугольник
- Видео
- Тренажер
- Теория
Заметили ошибку?
Угол. Прямой и развернутый угол. Чертежный треугольник.
Углом называют фигуру, образованную двумя лучами, выходящими из одной точки.
Лучи, образующие угол, называют сторонами угла, а точку, из которой они выходят, – вершиной угла.
На рисунке сторонами угла являются лучи ОА и ОВ, а его вершиной – точка О. Этот угол обозначают так: АОВ.
При записи угла в середине пишут букву, обозначающую его вершину. Угол можно обозначить и одной буквой – названием его вершины. Например, вместо «угол АОВ» пишут короче «угол О», если с такой вершиной на рисунке только один угол и это не создаёт путаницы. Вместо слова «угол» пишут знак ∠, получается ∠АОВ или ∠О.
На рисунке точки N и D лежат внутри угла КОМ, точки T и H лежат вне этого угла, а точки Р, С, В лежат на сторонах угла КОМ.
Как и все геометрические фигуры, углы сравниваются с помощью наложения. Если один угол можно наложить на другой так, что они совпадут, то эти углы равны.
Углы бывают: развернутые, прямые, острые и тупые.
Развернутый угол образован двумя лучами, которые дополняют друг друга. Стороны этого угла составляют прямую линию, на которой лежит вершина развернутого угла.
Если согнуть два раза пополам лист бумаги, а потом развернуть его, то линии сгиба образуют 4 равных угла. Каждый из этих углов равен половине развернутого угла. Такие углы называют прямыми.
Прямым углом называют половину развернутого угла.
Для построения прямого угла пользуются чертежным треугольником. Чтобы построить прямой угол, одной из сторон которого является луч ОА, надо:
- Расположить чертежный треугольник так, чтобы вершина его прямого угла совпала с точкой О, а одна из сторон пошла по лучу ОА.
- Провести вдоль второй стороны треугольника луч ОВ.
Заметили ошибку?
Расскажите нам об ошибке, и мы ее исправим.
Содержание:
- Определение развернутого угла
- Примеры решения задач с развернутыми углами
Определение развернутого угла
Определение
Развернутый угол — это угол,
стороны которого составляют прямую (рис. 1).
Градусная мера развернутого угла равна $180^{circ}$.
Любой луч, проведенный из вершины развернутого угла, делит его на два угла. Полученные в результате углы имеют
одну общую сторону, а две другие составляют прямую. Такие углы называются смежными.
Биссектриса развернутого угла делит его на два
прямых угла.
Если произвольный луч, проведенный из вершины развернутого угла, не является биссектрисой,
то он делит развернутый угол на два, один из которых острый (меньше прямого), а другой — тупой (больше прямого)
Примеры решения задач с развернутыми углами
Пример
Задание. Развернутый угол разделен лучом на два угла,
градусные меры которых относятся как 1:4.
Найдите полученные углы.
Решение. Обозначим искомые углы как
$alpha$ и
$beta$ . Пусть
$x$ — коэффициент пропорциональности, тогда
$alpha = x$, а соответственно
$beta = 4x$ . Так как градусная мера развернутого угла равна
$180^{circ}$ и согласно свойствам угла, что градусная мера
угла равна сумме градусных мер углов, на которые он разбивается любым лучом, проходящим между его сторонами, то делаем вывод, что
$$x+4 x=180^{circ} Rightarrow 5 x=180^{circ}$$
Отсюда находим:
$x=alpha=36^{circ}$ и $beta=4 x=4 cdot 36^{circ}=144^{circ}$
Ответ. $36^{circ}$ и $144^{circ}$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
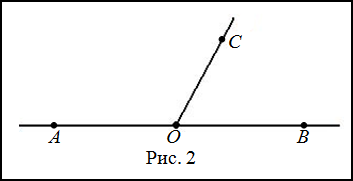
Пример
Задание. Луч
$OC$ делит развернутый угол
$AOB$ на два угла
$AOC$ и
$BOC$ так, что угол
$AOC$ на
$30^{circ}$ больше угла
$BOC$ . Найти углы
$AOC$ и
$BOC$ .
Решение. Изобразим заданный развернутый угол и проведем луч
$OC$ (рис. 2).
Пусть $angle B O C=x^{circ}$, тогда из условия получаем, что
$angle A O C=(x+30)^{circ}$. Так как эти углы являются
смежными, то их сумма равна
$180^{circ}$, то есть
$$angle A O C+angle B O C=180^{circ}$$
а тогда
$$x+x+30=180 Rightarrow 2 x=150 Rightarrow x^{circ}=angle B O C=75^{circ}$$
Отсюда
$$angle A O C=(x+30)^{circ}=105^{circ}$$
Ответ. $angle A O C=105^{circ}, angle B O C=75^{circ}$
Читать дальше: что такое вертикальные углы.
Определение угла
Угол — это простая геометрическая фигура. Определение угла напрямую связано с понятием луча.
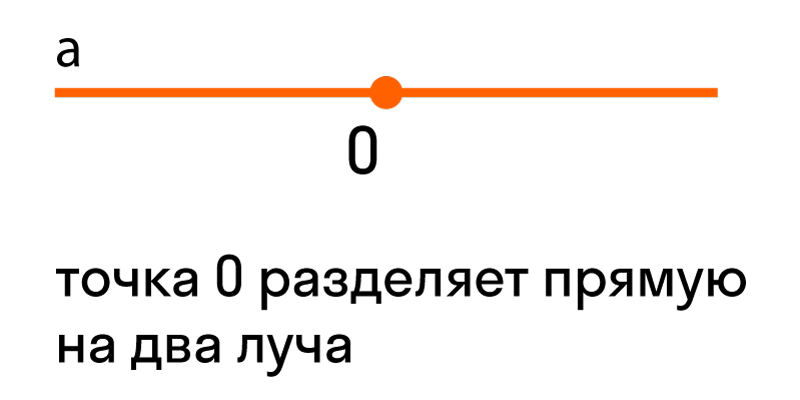
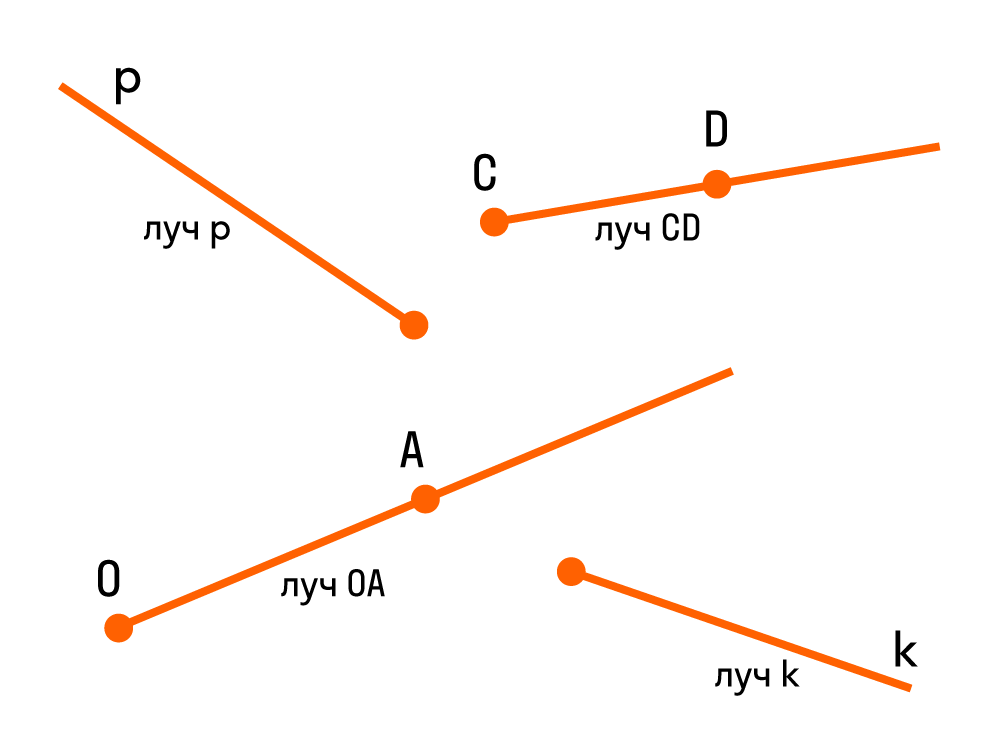
Луч — прямая линия, у которой есть начало, но нет конца, и продолжается она только в одну сторону.
Если нам дана прямая a на плоскости, и на ней есть некоторая точка O — выходит, что прямая разделена точкой на две части, каждая из которых является лучом с началом в точке O.
Луч можно обозначить одной строчной буквой латинского алфавита или двумя прописными. Например, вот так:
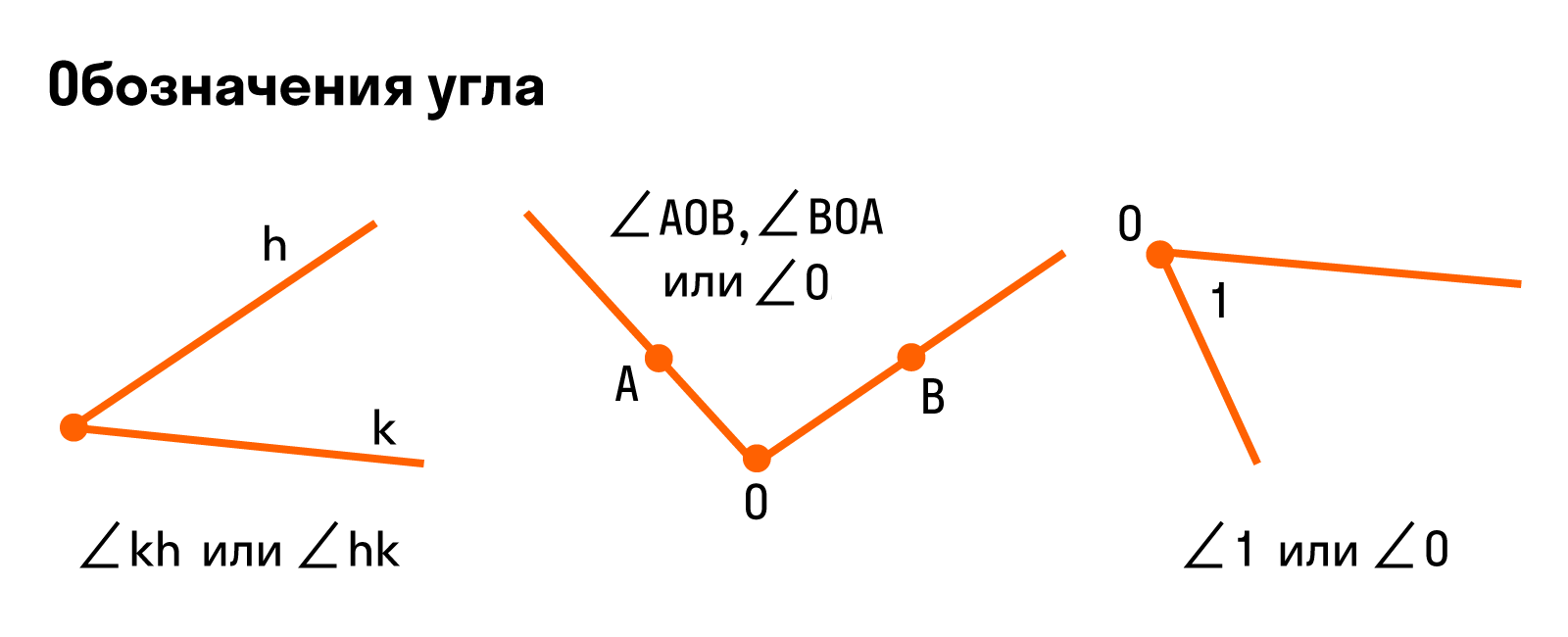
Угол — часть плоскости между двумя линиями, исходящими из одной точки. Каждая сторона угла является лучом, а вершина — общим началом сторон.
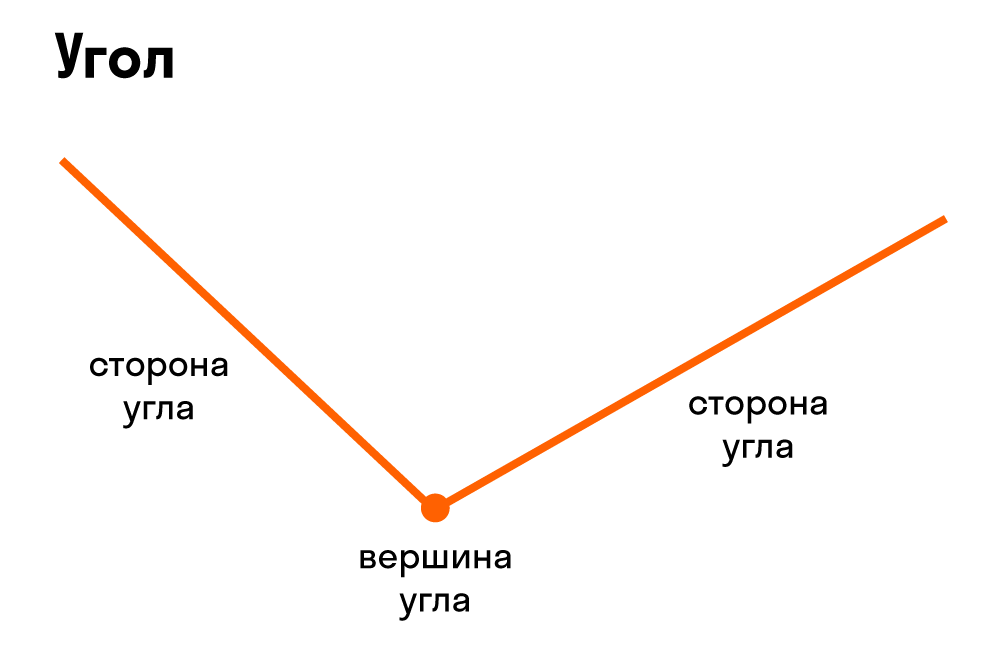
Что такое вершина и стороны угла
В математике существует специальный символ для обозначения угла, вот он: ∠.
Если стороны угла названы малыми латинскими буквами, то их записывают после символа. Например, так: ∠ab или ∠ba.
Если стороны угла названы большими буквами, то обозначение угла будет состоять из символа и трех букв, при этом вершина всегда записывается в центре. При сторонах угла OA и OB название угла запишем так: ∠AOB и ∠BOA. Также можно назвать угол одной большой буквой, которая указывает на его вершину, например: ∠O.
Иногда встречается обозначение в виде цифр — так тоже можно.
Для наглядности — все способы обозначения углов:
Так как угол делит плоскость на две части, одна будет внутренней областью угла, а другая — внешней областью угла. Вот так:
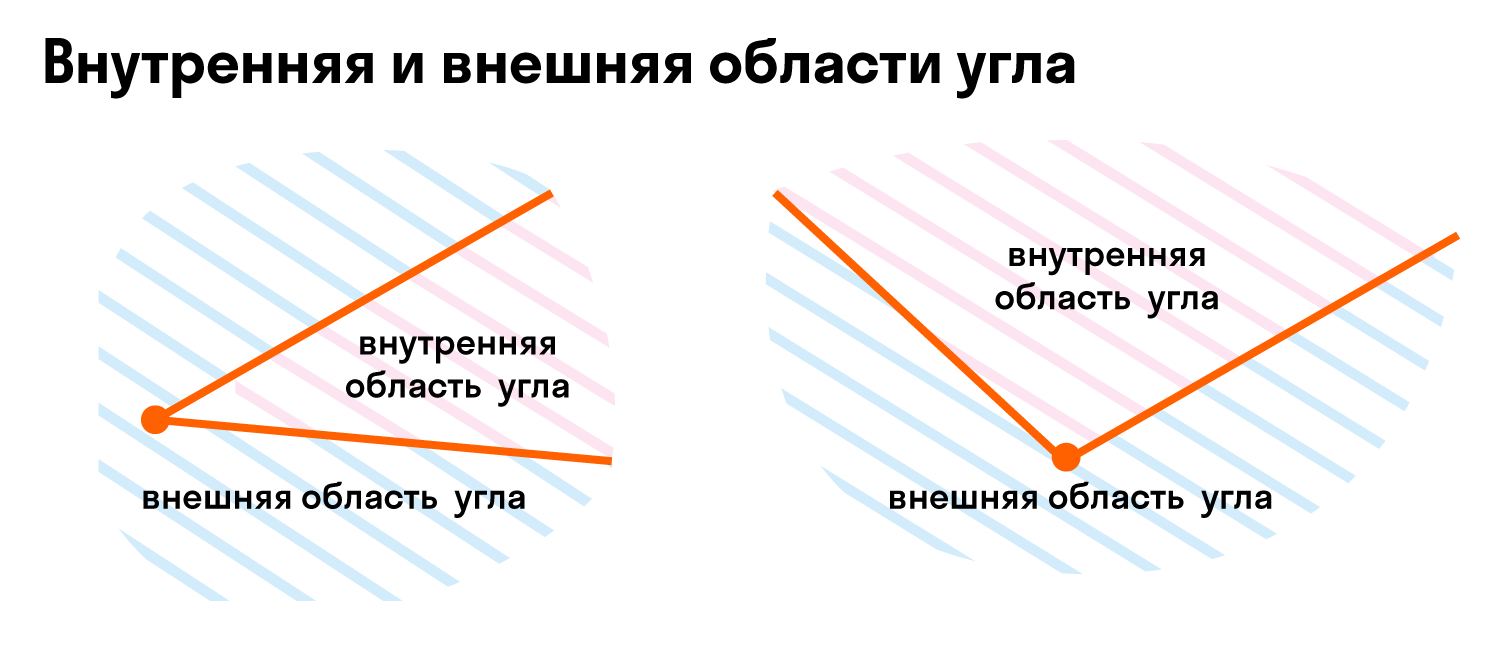
Единица измерения углов — градусы. Символ для обозначения градуса угла: °.
Получай лайфхаки, статьи, видео и чек-листы по обучению на почту
Узнай, какие профессии будущего тебе подойдут
Пройди тест — и мы покажем, кем ты можешь стать, а ещё пришлём подробный гайд, как реализовать себя уже сейчас
Виды углов
Есть разные типы углов и у каждого своё название:
- острый
- прямой
- тупой
- развернутый
- выпуклый
- полный
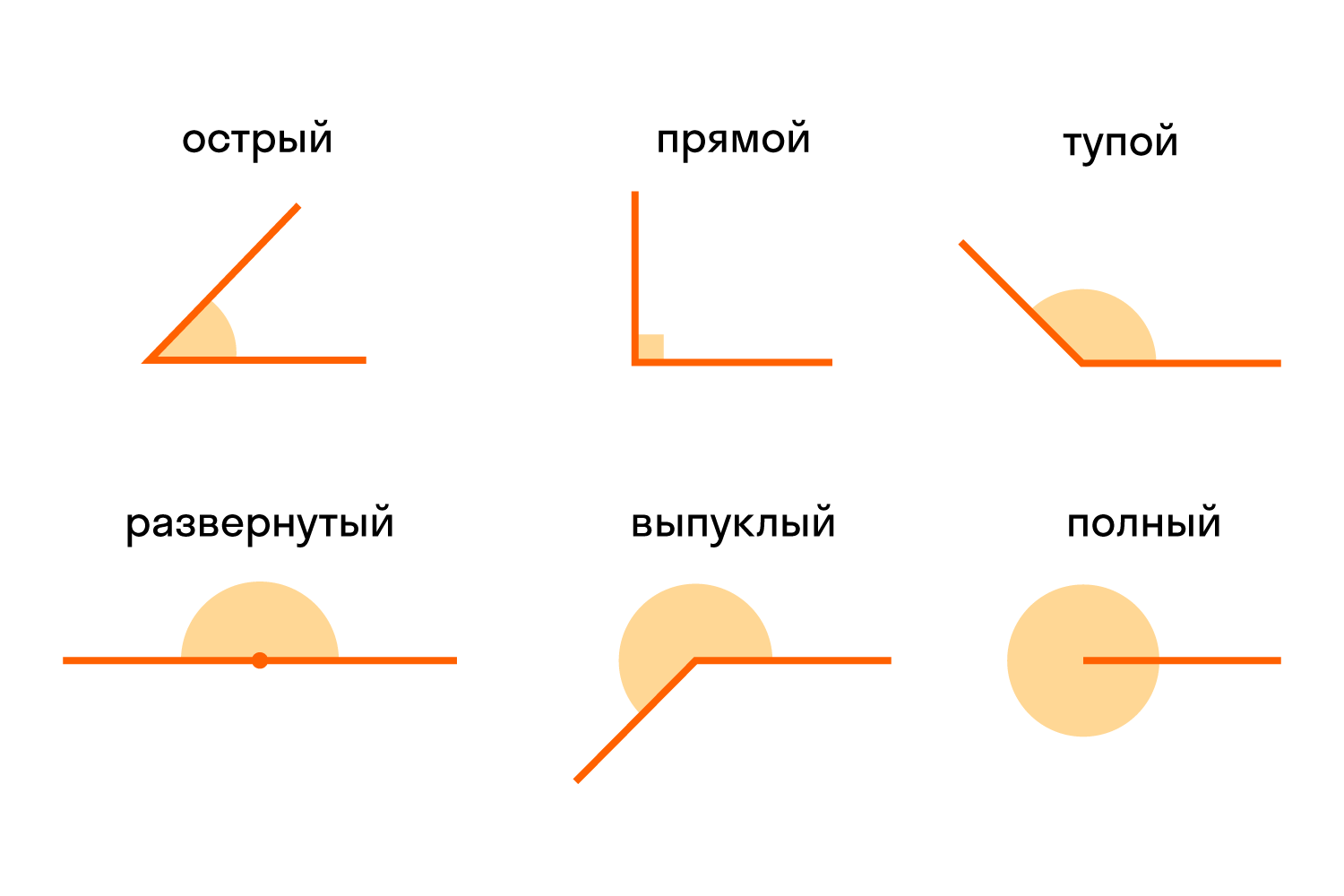
Различать виды углов в геометрии важно. Определять можно на глаз или с помощью линейки.
Прямой угол — это угол, стороны которого перпендикулярны друг другу. Прямой угол всегда равен 90°.
Если два смежных угла равны между собой, то каждый из них является прямым. Для удобства прямой угол обозначается уголком. Вот так:
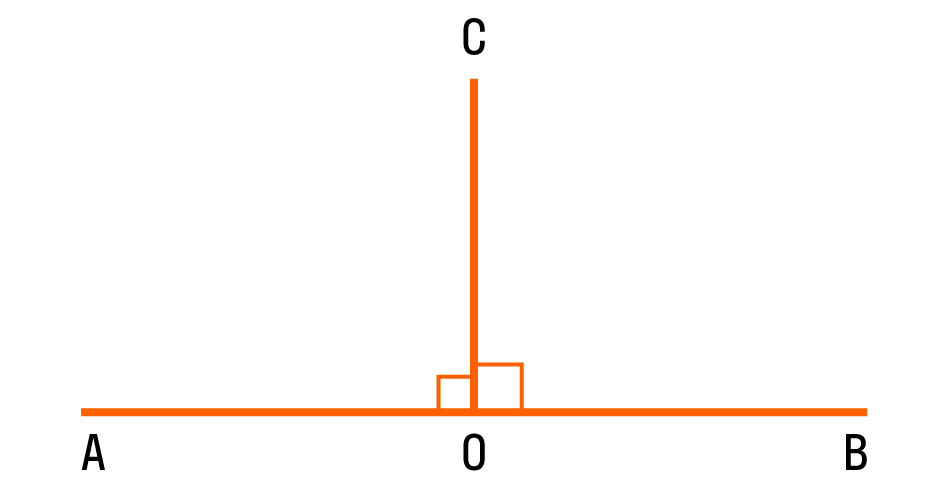
На картинке изображены два прямых угла ∠AOC и ∠COB. Общая сторона OC перпендикулярна прямой AB, а точка O — основание перпендикуляра.
Острый угол — это угол, который меньше прямого угла, то есть < 90°.
Развернутый угол — это открытый угол, который образован двумя лучами и равен сумме двух прямых углов. Развернутый угол равен 180°. Как выглядит развернутый угол, показано на первой картинке.
При разделении развернутым углом на плоскости любая из его частей считается внутренней областью развернутого угла.
Неразвернутый угол — это любой угол, который не является развернутым, то есть не равен 180°.
Тупой угол — это угол, который больше прямого угла, но меньше развернутого:
90° < тупой угол < 180°.
Выпуклый угол — это угол, который больше развернутого угла, но меньше полного:
180° < выпуклый угол < 360°.
Полный угол — это угол, обе стороны которого совпадают с одним лучом. Он равен сумме четырех прямых углов, то есть = 360°.
Прилежащие углы — это пара углов с общей вершиной и стороной, другие стороны при этом лежат по разные стороны от общей стороны.
На картинке мы видим два прилежащих угла ∠AOB и ∠BOC, общую вершину O и общую сторону OB.
Можно сформулировать определение по-другому: если из вершины любого угла провести луч, разделяющий угол на два, то образованные углы будут прилежащими.
Чтобы найти угол, который разделен лучом, нужно сложить полученные углы: ∠AOB = ∠AOC + ∠COB. Из этого можно выделить следующие верные разности:
- ∠AOC = ∠AOB − ∠COB,
- ∠COB = ∠AOB − ∠AOC.
Запоминаем!
Угол называется прямым, если он равен 90°, острым, если он меньше 90°, тупым, если он больше 90°, но меньше 180°. Развернутый угол равен 180°.
Онлайн-школа Skysmart приглашает детей и подростков на курсы по математике — за интересными задачами, новыми прикладными знаниями и хорошими оценками!
Сравнение углов
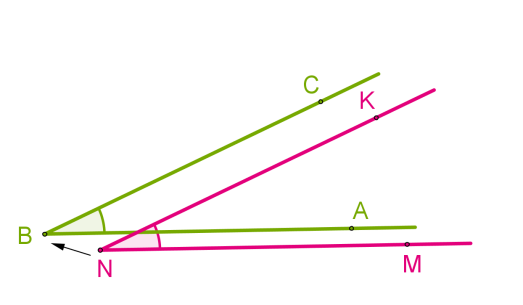
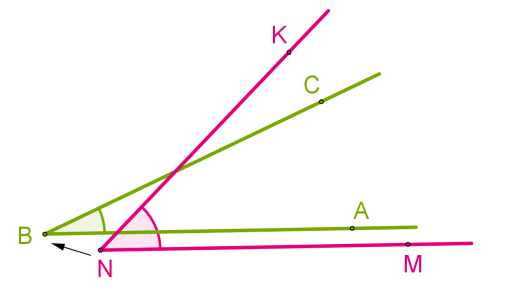
Для сравнения углов можно использовать самый простой способ из программы 4 класса — метод наложения. Для этого нужно совместить две вершины и сторону одного угла со стороной другого. Если стороны заданных углов совпадут, значит углы равные. Если нет, то угол, который лежит внутри другого, будет меньшим. Здесь два наглядных примера с равными и неравными углами:
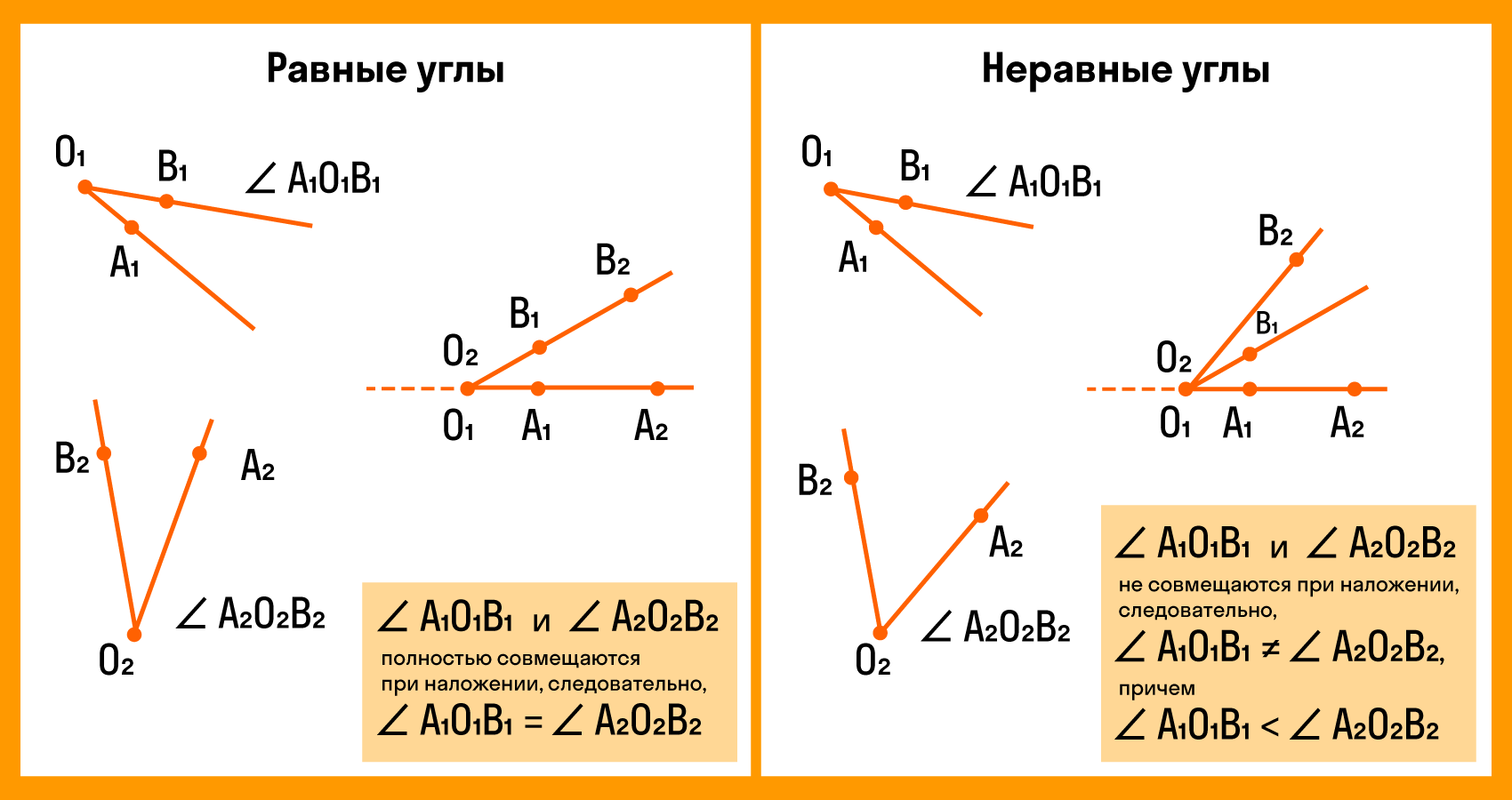
При этом развернутые углы всегда являются равными.
Совмещение углов ∠𝐴𝐵𝐶 и ∠𝑀𝑁𝐾 происходит следующим образом:
- Вершину 𝐵 одного угла совмещаем с вершиной 𝑁 другого угла.
- Сторону 𝐵𝐴 одного угла накладываем на сторону 𝑁𝑀 другого угла так, чтобы стороны 𝐵𝐶 и 𝑁𝐾 располагались в одном направлении.
Если совпадут и другие стороны, то углы равны: ∠𝐴𝐵𝐶 = ∠𝑀𝑁𝐾.
Если нет, то один угол — меньше другого: ∠𝐴𝐵𝐶<∠𝑀𝑁𝐾.
Сравнить углы можно также, измерив их величины. Для этого понадобится специальный инструмент для построения и измерения углов — транспортир. Вот как он выглядит:
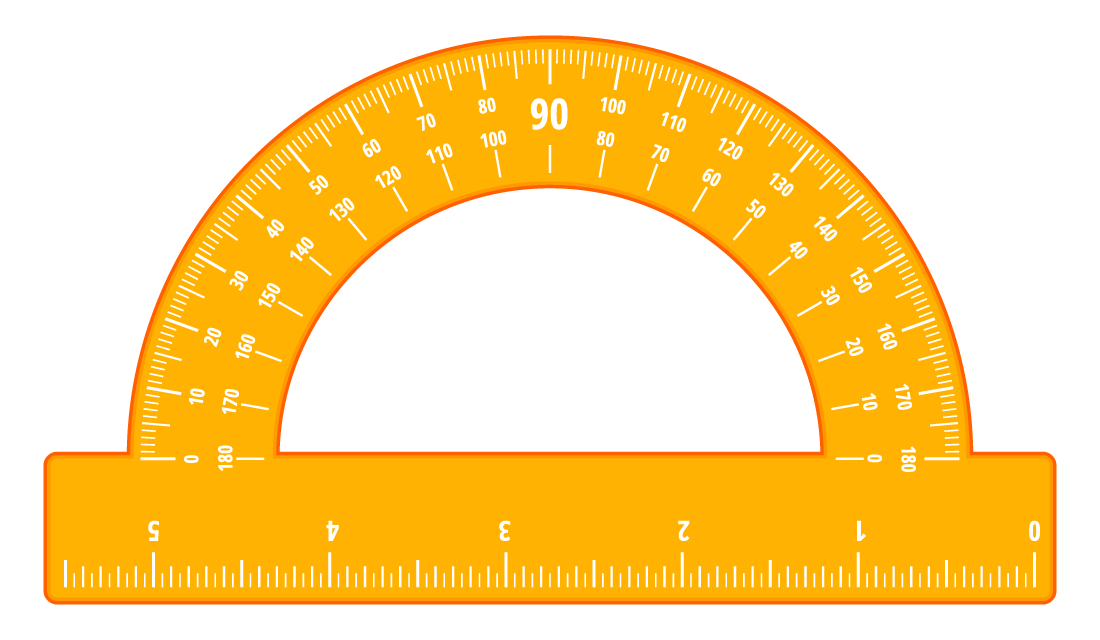
Как правильно измерять углы
Измерение углов похоже на измерение отрезков: нужно сравнить их с углом, принятым за единицу измерения. В геометрии обычно за единицу измерения принимают градус — угол, равный 1/180 части развернутого угла. Он обозначается так: °.
Градусная мера угла — положительное число, которое показывает, сколько раз градус и его части укладываются в данном углу.
Есть еще две возможные меры угла: минуты и секунды. Они позволяют выполнять более точные расчеты, особенно, когда величина не является целым обозначением градуса.
Минута — 1/60 часть градуса. Обозначается ´.
Секунда — 1/60 часть минуты. Обозначается ´´.
Градус состоит из 3600 секунд, то есть: 1° = 60´ = 3600´´.
Как происходит измерение угла: сначала измеряют стороны угла, а после — его внутреннюю область. Всегда нужно считать количество уложенных углов, так как они предопределяют меру измеряемого угла.
Когда луч делит угол на два или более углов, градусная мера всего угла равна сумме градусных мер этих углов.
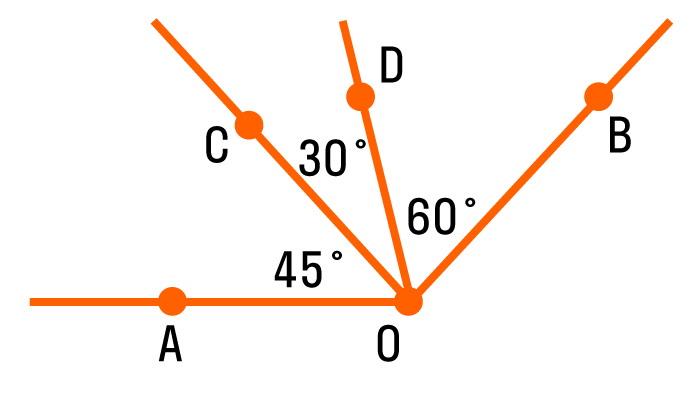
На рисунке изображен угол АОВ, он состоит из углов АОС, СОD и DОВ. Можно записать так: ∠AOB = ∠AOC + ∠COD + ∠DOB = 45° + 30° + 60° = 135 °.
Равные углы имеют равную градусную меру.
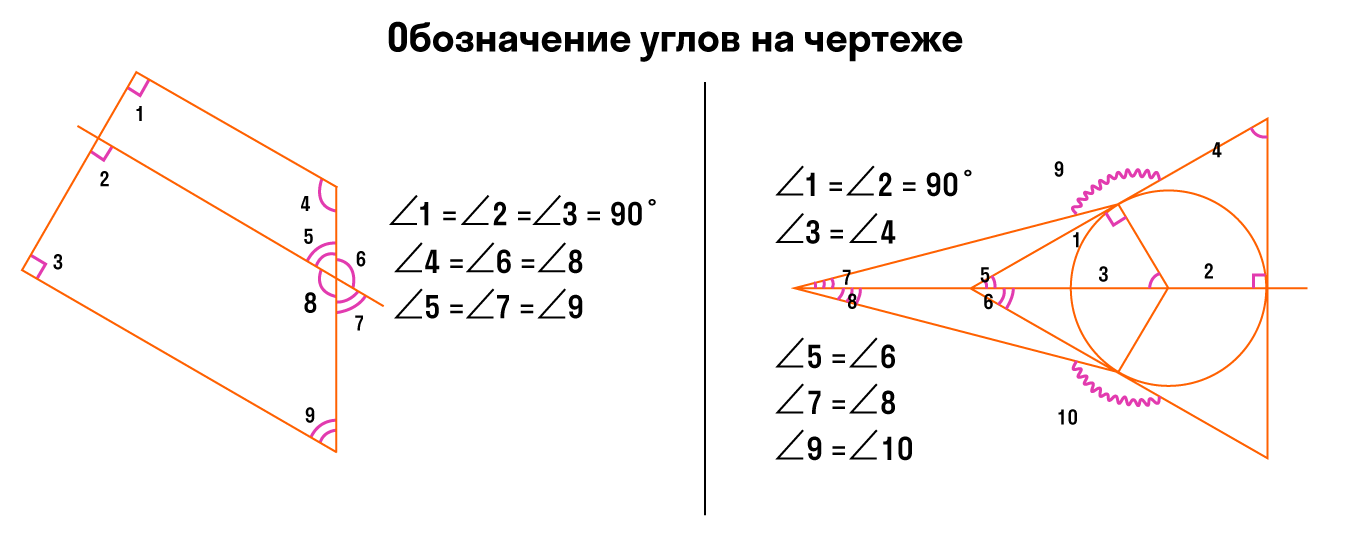
Обозначение углов на чертеже
Чертеж помогает решать задачки по геометрии в разы быстрее. Чтобы наглядно изображать углы и прочие фигуры, придумали даже отдельное направление — геометрический чертеж.
Задачи с углами могут быть разными, и не всегда есть возможность правильно изобразить и отметить угол. Вот что важно запомнить при обозначении лучей и углов:
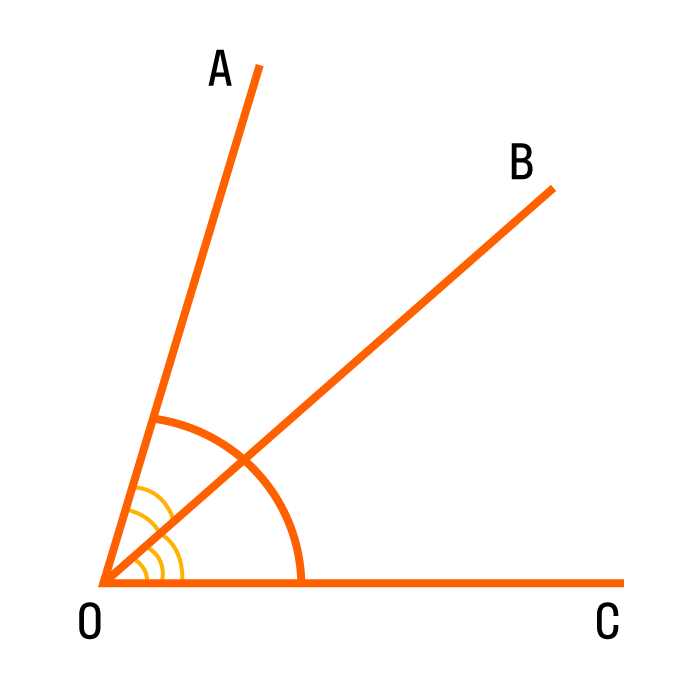
- Равные углы обозначают одинаковым количеством дуг.
- Неравные углы обозначают разным количеством дуг, чтобы они отличались между собой.
На чертеже отмечены три неравных угла:
Для обозначения на чертеже более трех углов используем разные виды дуг: волнистые, зубчатые.
Обозначать углы можно разными цветами. Главное, чтобы было просто и броско. При этом не обязательно отмечать все-все углы — достаточно только тех, которые нам нужны для решения задачки.