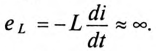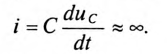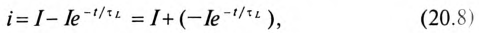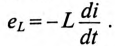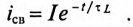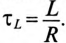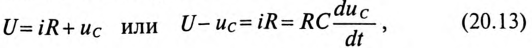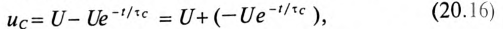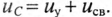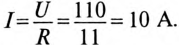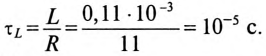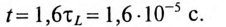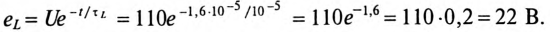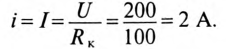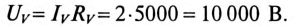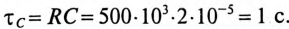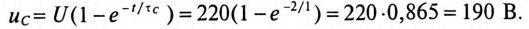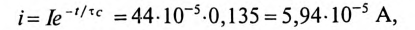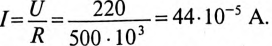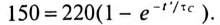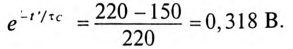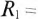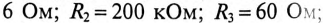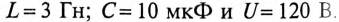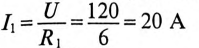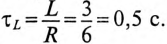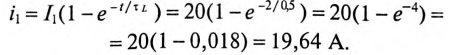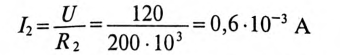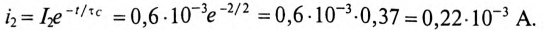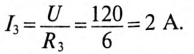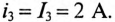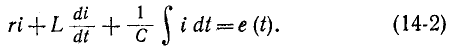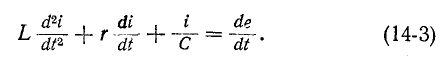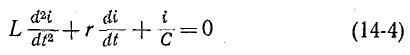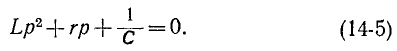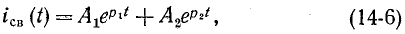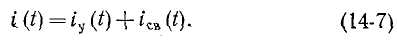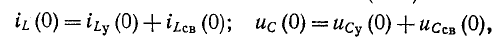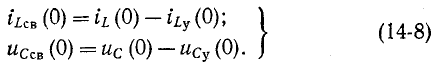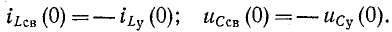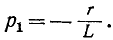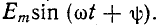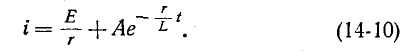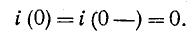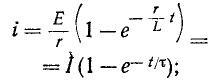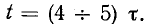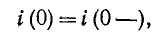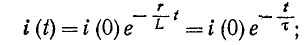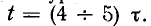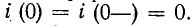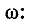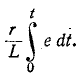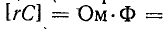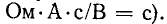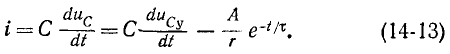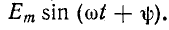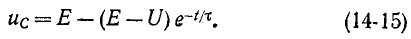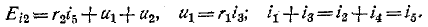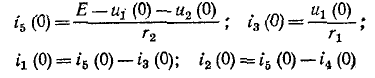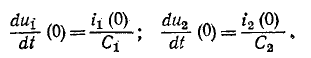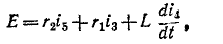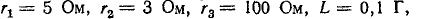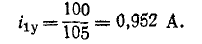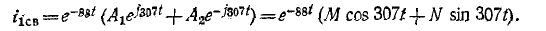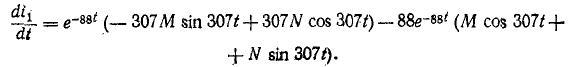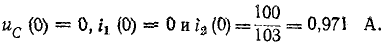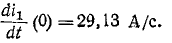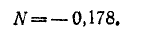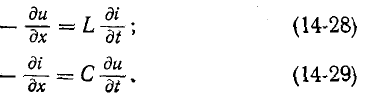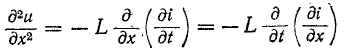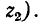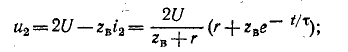Довольно неприятная ситуация, знакомая многим – без каких-либо видимых причин свет в квартире (доме) или в некоторых комнатах вдруг гаснет, бытовая техника отключается. И вместе с тем явно видно, что у соседей с подачей электричества — все нормально. Первая реакция у всех, наверное, одинаковая – хозяева проверяют, не выбило ли автомат или не перегорела ли пробка-предохранитель.
Если это действительно так, и при перезапуске автомата (замене пробки) работоспособность домашней электросети восстанавливается, то задача упрощается. Безусловно, с причиной срабатывания защиты разобраться надо — возможно, была превышена допустимая нагрузка. Но, во всяком случае, проводка исправна. Но если напряжение на выходе с предохранителей есть, а в помещениях отсутствует – где-то случился обрыв. И предстоит непростая задача восстановления домашней сети.
Один из самых сложных вопросов в этом случае будет – как найти обрыв провода в стене. Его и рассмотрим в настоящей публикации.
Возможные причины неисправностей проводки
Чтобы легче было выявлять участок, на котором произошло несанкционированное размыкание цепи питания, необходимо представлять, какие причины могут вызвать подобные неисправности. Следует сразу заметить, что чаще всего они обусловлены ошибками в монтаже домашней электрической сети или нарушениями правил ее эксплуатации. Сама по себе проводка, да еще замурованная в стены, обрывается крайне редко, хотя и такого варианта полностью исключать нельзя.
- Очень часто контакт пропадает на клеммных соединениях – начиная от автоматов в распределительном щите и заканчивая розетками, выключателями или даже конечными приборами потребления. Плохо затянутая или ослабшая со временем клемма начинает греться, искрить, отчего дефект «прогрессирует», что рано или поздно заканчивается полным исчезновением электрического контакта.
- Соединения в монтажных коробках, если они выполнены с нарушениями или недостаточно качественно – еще одно уязвимое место. Особую опасность представляют кустарные скрутки проводов, которые горе-мастера просто закрывают сверху слоем изоленты – и считают, что этого достаточно. Нет, безусловно, и скрутка может быть надежной и долговечной, но иногда встречаются такие картины, что лучше бы их не видеть. Например, наличие в одной скрутке медных и алюминиевых проводов, что категорически запрещено, попытка соединения одножильного толстого жёсткого проводника с гибким многопроволочным. Или использование клемм, которые явно не подходят по токовой нагрузке для данной линии. Скажем, клеммы Wago — очень удобны в монтаже, но все же их предназначение, скорее — коммутация линий, выделенных под освещение помещений. А вот на участках проводки, от которых питается мощная бытовая техника, они вполне могут и подвести.
Кстати, перечисленные выше причины, хотя и неприятны сами по себе, все же довольно легко диагностируются и устраняются. Кроме того, обычно такие обрывы не происходят совсем уж внезапно – как правило, они начинают «сигнализировать» хозяевам о нарастании проблемы — мерцаем света, явными признаками искрения, запахом подгоревшей изоляции или пластика. То есть при внимательном отношении к своему электрохозяйству владельцам дома или квартиры предоставляется «гандикап» на обнаружение и устранение неполадок.
Типичные неполадки в домашней электросети и их устранение
Понятно, что если вообще нет никакого понятия об электромонтажных работах, нечего и браться за такое дело самостоятельно – лучше вызвать специалиста. Но все же хорошему хозяину многое по силам исправить и самому. На страницах нашего портала можно найти подробные инструкции по ремонту розеток, по выявлению причин срабатывания УЗО или частого выбивания автоматического выключателя.
Гораздо сложнее справиться с дефектами скрытого характера, с разрывами электрической цепи на участках проводки, спрятанных в стене.
- Они, кстати, тоже очень часто появляются по причинам, так сказать, субъективного характера. «Классический» пример – сверление стены или забивание гвоздя без предварительной «разведки» на предмет прохождения на этом участке скрытой проводки.
Сложно назвать это удачей, но если после сверления сразу пропадает напряжение в сети, то, по крайней мере, причина становится очевидной. Но бывает и иначе – сверло или гвоздь задевают провод по касательной, нарушая изоляцию и лишь слегка повреждая проводник. В таких случаях не исключено, что проводка еще будет служить, причем иногда – весьма немало. Но в месте нарушения целостности провоцируются токи утечки (а если нет УЗО, то выявить их удается не сразу), снижается нормальная проводимость, возрастает сопротивление на локальном участке, не исключается постепенное плавление изоляции с последующим коротким замыканием. То есть окончательный разрыв может случиться в любой момент, даже через довольно продолжительное время, и его непросто будет сопоставить с проводимыми когда-то сверлильными работами.
В идеале, хозяин квартиры (дома) должен точно знать трассы прокладки проводки в своих владениях и расположение монтажных коробок. Задача упрощается, если электромонтажные работы выполнялись в строгом соответствии с правилами и рекомендациями. То есть все участки скрытой проводки расположены строго горизонтально и вертикально. Однако, картины, сходные с той, что показана на иллюстрации ниже, видели, наверное, многие электрики, которых вызывали для устранения аварий. Понятно, что при такой «схеме» разводки домашней электросети любое сверление стены или забивание гвоздя превращается в «лотерею»: повезет – не повезет.
- Сама по себе проводка, замурованная в стены, дает обрыв не столь часто. Но и эту вероятность нельзя сбрасывать со счетов. Такими дефектами особо могут «грешить» старые провода, проложенные много десятилетий назад. И в особенности – если в доме все еще используется алюминиевая проводка.
Со временем проводка, безусловно, стареет. Это, прежде всего, выражается в том, что пластиковая изоляция теряет свою эластичность, становится хрупкой, трескается. Мелкие трещины могут стать причиной вначале, казалось бы, незначительных утечек тока. Ну а о том, что такие утечки имеют свойство возрастать — выше уже говорилось.
При прокладке проводки мог получиться залом проводника. Он тоже вполне способен проявиться не сразу, а спустя время, причем, исчисляемое годами. То есть проложить какую-то логическую связь с внезапно появившимся обрывом – практически невозможно. Просто на таком локальном участке за счет повреждения нормальной кристаллической структуры металла может значительно возрасти сопротивление, что вызывает перегрев, еще большую деструктуризацию проводника, плавление изоляции, короткое замыкание и прочие «радости».
Такие аварии – самые сложные в диагностике и определении конкретного места разрыва цепи. Внешних признаков – практически не бывает. И если даже почувствуется какой-то отдаленный «аромат» подгоревшей изоляции, отыскать источник запаха – вряд ли удастся.
Все перечисленное выше может, конечно, случиться с любой проводкой. Но если в доме (квартире) все еще используются алюминиевые провода – вероятность аварийных ситуаций возрастает в разы. Этот металл значительно уступает меди и проводимостью, и коррозионной устойчивостью, и механической прочностью. Мало того, алюминий, как выражаются многие электрики, «плывет» в клеммах или скрутках. То есть даже качественно обжатый контакт со временем вполне может потерять надежность, начать греться и искрить.
Это – еще один довод при любой возможности избавляться от старой алюминиевой проводки и переходить на качественные медные кабели.
Какие кабели приобретать для прокладки домашней проводки?
Если говорить о материале – то, конечно, исключительно медные. А если о конкретной марке и сечении – то здесь требуется владеть некоторой важной информацией. Подробнее о типах кабелей для проводки в доме или квартире – читайте в специальной публикации нашего портала.
Как отыскать обрыв провода в стене
Первые шаги и проверка распределительного щита
Итак, пока по неизвестным причинам в комнате (одной, нескольких или всех сразу) погас свет, перестали работать электроприборы. Первое естественное действие хозяев – проверить, не общее ли это выключение по улице (подъезду городского дома). Если нет – обращается внимание на распределительный щит – не выбило ли автоматы или не перегорели ли плавкие предохранители — пробки (кое –где еще встречается и такой анахронизм).
Если и здесь все в норме – предстоит поиск неисправностей уже в своих владениях.
С чего начинают. Прежде всего – с «включения логики». Стоит сразу же проанализировать, не проводилось ли недавно в квартире работ, связанных со сверлением стен. Не было ли за последнее время других чрезвычайных происшествий, например, потопа от соседей сверху.
Надо постараться припомнить, были ли какие-то «симптомы заболевания» проводки – моргание света, характерный треск искрения контактов, запах подгоревшей изоляции. Иногда даже такой информации бывает достаточно, чтобы с большой долей точности быстро обнаружить место аварии.
Поиск неисправностей начинают всегда вести от распределительного щитка. Первое – визуальный контроль. Если авария произошла именно здесь, она может выдать себя выскочившим из клеммы или почерневшим контактом на автомате (УЗО). Рекомендуется сразу, вооружившись мультиметром, установленным на измерение переменного напряжения более 250 вольт, проверить, имеется ли напряжение на вводном автомате. Если показания измерения – в норме, однозначно грешить на подачу не нужно, и причина точно находится внутри квартиры.
Проверить, конечно, можно и индикаторной отверткой, но она способна показать только наличие фазы. А это – неоднозначная картина, так как обрыв может быть и по нулевому проводу.
Некоторые советуют использовать для проведения подобной диагностики простейший прибор, состоящий из патрона с лампой и двух проводов. Действительно, таким способом, пожалуй, легче всего определить, имеется ли в данном месте (на клемме автомата, в распределительной коробке, в розетке и т.п.) нужное напряжение в 220 вольт. Однако, работа с подобным самодельным «тестером» является весьма небезопасной, и правилами охраны труда — категорически запрещена. И автор, как «законопослушный гражданин», тоже не рекомендует таких способов проверки.
Отсутствие мультитестера не должно являться оправданием. В наше время приобрести совсем недорогой, но в то же время вполне «дееспособный» тестер сможет каждый. И такой прибор должен, наряду с индикаторной отвёрткой, быть у любого хорошего хозяина. Так что будем исходить из посыла, что мультиметр в наличии есть.
После проверки вводной автомат выключается, равно, как и все другие автоматы. И следующим шагом проверяется надежность зажатия проводников в клеммах на всех АВ и УЗО, а также в шинах нуля и заземления. При необходимости – производится подтяжка. Случается и так, что на этом устранение аварии и заканчивается – все, оказывается, крылось в плохом контакте на одной из клемм.
Кстати, уместно, наверное, будет сразу заострить внимание на некоторых распространенных ошибках, которые частенько допускаются неопытными мастерами при подключении проводов к клеммам автомата (УЗО).
- В клемме зажимается медный многопроволочный гибкий проводник без оконцовки. Даже при, казалось бы, качественной обтяжке, контакт со временем может сильно ослабнуть. Или даже вовсе исчезнуть – пережатые тонкие проволочки могут обламываться. В щите вообще лучше не использовать такие провода – надежнее будет одножильный нужного сечения. Но если уж некуда деваться, то провод в обязательно порядке должен заканчиваться клеммным наконечником. Стоят такие детали недорого, их установка – труда не составляет, но контакт получится надежным.
- При подключении провода его зачищенный конец слишком глубоко заводится в клемму. И при затяжке контактная площадка начинает упираться в слой изоляции. Понятно, что обжим самого проводника получается при этом ненадежным, что становится предпосылкой для искрения, нагрева, пропадания контакта.
- В одну клемму подключается два провода разного сечения. Контактная площадка при затяжке клеммы упирается в больший по сечению проводник, а контакт на меньшем при этом очень часто становится крайне ненадежным
Чтобы уже полностью закончить со щитом, можно, включив автомат на вводе, последовательно проверить работоспособность всех остальных автоматических выключателей, дифавтоматов и УЗО. Понятно, что с каждого из них, если тот находится во включённом положении, должна выходить фаза. Здесь для проверки будет достаточно индикаторной отвертки. Или опять же применяется мультитестер – замеряется напряжение между выходом автомата (УЗО, АВДТ) и общей шиной нуля.
Убедившись в том, что с распределительным щитом – все в норме, можно переходить к поиску аварийного участка уже в самой квартирной разводке.
Локализация места аварии
Все перечисленные выше действия будут уместны, если напряжение пропало разом во всем помещениях. Но при обрыве провода на каком-то конкретном участке чаще всего и исчезновение питания также ограничивается какой-то областью квартиры или дома. Безусловно, если распределительный щит был смонтирован грамотно, с разветвлением общей подачи после счетчика по отдельным линиям.
У хорошего хозяина так обычно и бывает – выделяется несколько розеточных групп, в том числе — и на отдельные розетки для мощной бытовой техники (стиральные машины, электроплиты, духовки, насосное оборудование и т.п.). Освещение также может быть разделено на группы, например, по помещениям. Если все организовано именно так, на автоматах имеются подписи (или нумерация с «легендой»), то задача существенно упрощается.
То есть если пропало напряжение на какой-то определенной розеточной группе, но проверка остальных показывает, что все в норме, то сразу ясно – обрыв на конкретной линии. Аналогично и с освещением, если оно погасло только в отдельной комнате (группе комнат), но в других свет горит, и розетки работают.
Узнайте, как рассчитать освещение по площади помещения, изучив алгоритм и удобные калькуляторы онлайн, в специальной статье на нашем портале.
Но часто бывает и так, что все распределение сводится к одному-двум автоматам, и картина поучается неясной. Кроме того, некоторые хозяева могут просто не знать «легенды» своего щита, если они приобрели квартиру или дом с уже проложенной электросетью, и до текущего момента их этот вопрос пока не занимал. И настоятельно рекомендуется посвятить этому время, чтобы опытным путем все же добиться ясности, какой прибор в щитке за что отвечает.
Поиск же участка обрыва ведется от щита к точке, где выявлено пропадание напряжения (розетке, осветительному прибору). Участки могут быть следующими:
- Трасса от щита до распределительной коробки.
- Участок от распределительной коробки до розетки (выключателя).
- Участок между выключателем или коробкой и осветительным прибором.
Нередко встречаются разводки, в которых проводка к розеточным группам не предусматривает распределительных коробок, то есть провод идет непосредственно от щита к конечной точке. Причем, от одной розеточной группы к последующей также может быть протянут кабель. Это сразу бывает заметно, когда к розетке подходит два кабеля: один из них идет от щита, другой – далее на следующую группу.
Итак, следующая задача – точно определить участок, на котором произошел обрыв.
Поиск участка проводки с обрывом
Задача эта непростая и довольно утомительная, особенно если отсутствует схема проложенной проводки. Но все же после первичной локализации аварии, хотя бы по помещению или линии, выполнить ее будет проще.
Поиск начинают вести от распределительного щита. Каким образом это можно сделать?
Индикаторная отвёртка помогает определить, есть ли фаза там, где ей положено быть. Например, фаза есть на выходе с соответствующего автомата, далее – в распределительной коробке, но уже отсутствует на размещенной снизу розетке. Вывод напрашивается сам собой – место аварии находится между распределительной коробкой и розеткой.
Казалось бы – все просто, если бы не несколько «но»:
— Во-первых, такой метод помогает определиться исключительно с разрывами фазного провода. Но если оборван нулевой – результата получено не будет. Фаза может на розетке или осветительном приборе иметься, но сами приборы — оставаться в нерабочем состоянии.
— Во-вторых, такая проверка подразумевает работу со всклоченным напряжением в сети. Скажем честно – не лучший вариант для проводки, на которой явно есть авария, и тем более, если мастер не имеет достаточного опыта работы в электрике. Для проверки придется вскрывать распределительные коробки, разбираться со скрутками или клеммными соединениями в них, и по неопытности можно «наделать делов».
Кстати, индикаторная отвертка, помимо всего прочего, способна еще и исказить реальную картину. Случается, что свечение индикатора вовсе не говорит о наличии полноценной фазы, а только о каком-то потенциале, который вполне может быть обусловлен током утечки из другого «источника».
То же самое касается и замера напряжения с помощью мультиметра. И работа под напряжением – опасна, и показания напряжения могут быть весьма противоречивыми.
Как быть?
Самый надежный способ – это прозвон участков. Он сразу покажет целостность провода или наличие разрыва на нем. Используется для этого все тот же мультиметр, но только переведенный в режим измерения сопротивления, в позицию Ω. Во многих тестерах для такой цели вообще предусмотрен специальный режим: если участок цепи обладает нормальной проводимостью — прибор издает звуковой сигнал. Сопротивление медного провода невелико (при сечении 2,5 мм² – всего 0,7 Ома на 100 метров длины), то есть в масштабах дома или квартиры будет крайне несущественными — на индикаторе станет высвечиваться значение «0» или близкое к нему.
Для проведения такой ревизии, понятное дело, линию следует обесточить. После этого на щите отключаются все провода проверяемой линии – фазный от автомата, нулевой и заземления – от соответствующих шин.
Безусловно, просто так штатными проводами мультиметра прозвонку провести не удастся – тестируемые участки могут быть весьма длинными. Например, щит расположен в прихожей у входной двери, а распределительная коробка – в комнате. Значит, необходимо заранее подготовить «удлинитель» — отрезок гибкого медного провода нужной длины, чтобы хватало до самой удаленной точки, подлежащей проверке. Большого сечения не требуется — достаточно 1,0÷1,5 мм². Этот удлинитель, понятно, следует тоже заранее проверить на целостность, то есть прозвонить.
А чтобы соединения с концами проверяемых участков проводов не вызывало сложностей, удлинитель можно оснастить зажимом-«крокодилом» или, что даже проще и удобнее — клеммой WAGO с рычажным фиксатором. Не будет никаких проблем с подключением удлинителя к проверяемому проводу. Такую же клемму можно расположить и на втором конце удлинителя – свободное гнездо отлично подходит для вставки щупа тестера.
Первым начинают прозванивать участок от щита до распределительной коробки. Для этого в коробке иногда приходится разбирать выполненные там контактные соединения. Важно – перед разборкой необходимо запомнить (зарисовать, снять на камеру мобильника) то, как провода были подключены. Все это будет не столь сложно, если изоляция проводов имеет цветовую маркировку (синий – всегда нулевой, зелено-желтый – заземление, фаза может иметь различный цвет, но обязательно отличающийся от указанных). Если цветовой маркировки нет, то придется подписать провода, например, наклеив на них полоски малярного скотча.
Качественно, по всем правилам выполненные скрутки, конечно, лучше не разбирать – достаточно просто найти место, которого можно коснуться щупом при прозвонке.
Прозвонку каждого из проводов кабеля производят отдельно – получается, чтобы проверить участок предстоит выполнить два или три (при наличии заземляющего проводника РЕ) промера. Если все провода в норме, участок принимается за исправный. Желательно сразу, параллельно с прозвонкой, составлять схему, если ее ранее дома не было – она может еще пригодиться впоследствии. На схеме отмечается, что участок исправен, и переходят к следующему.
Обычно следующим идет кабель от распределительной коробки к розетке. Понятно, что розетку лучше заранее разобрать, чтобы получить доступ к контактам. Заодно – проверить и подтянуть контакты на клеммах.
Если же подключение розеток выполнено, минуя распределительные коробки, то получается и вовсе один прозвон, чтобы убедиться в целостности линии. Правда, если к розетке подходят два кабеля, то один из них, как уже говорилось выше, уходит на другую розеточную группу. Его следует отсоединить, чтобы проверить этот участок отдельно.
При проверке линии освещения приходится прозванивать чуть больше. Отдельно – линию питания от щита до коробки. Далее – нулевой провод от коробки до светильника (и провод РЕ, если он имеется). Затем – фазный провод от коробки до выключателя, затем – участок от выключателя до светильника.
Но в любом случае, как правило, вся проверка на ранее локализованной аварийной линии ограничивается прозвонкой двух-трех участков кабеля. И рано или поздно будет выявлен тот провод, на котором произошел обрыв. Следует проверить его несколько раз, чтобы убедиться в правоте своих умозаключений. Например, отсутствие проводимости может быть вызвано просто плохим прижимом щупа мультиметра к оголенному концу провода. Но после нескольких попыток «упрямое молчание» прибора все же докажет, что оборванный проводник найден.
Поиск точного места обрыва
Это, пожалуй, наиболее сложный этап проведения диагностики. И без специальных приборов зачастую желаемого результата не добиться.
Участок стены, в котором находится поврежденный кабель, необходимо тщательно обследовать визуально. Не исключено, что причиной стало механическое повреждение проводки – об этом уже говорилось.
Следует и сразу принять решение – будет ли заменяться весь участок проводки, либо в планах – отыскать место обрыва и постараться срастить проводник.
В том случае, если дефект, с большой долей вероятности, образовался по причине ветхости давно проложенных проводов, то лучше даже не морочить голову, а менять весь поврежденный участок (в идеале – и вовсе всю проводку в доме или квартире, но это уже требует капитального подхода). Нет никакой гарантии, что после проведения восстановительных работ аналогичный дефект не появится вновь, рядом с местом выполненного сращивания.
Поиск с помощью специальных детекторов проводки
Понятно, что для того, чтобы найти точку обрыва, необходимо для начала как минимум знать, где же конкретно в толще стены проходит кабель. Иными словами – знать, где искать. О правилах прокладки проводки уже вкратце говорилось выше. Даже расположение распределительных коробок, розеток и выключателей может стать подсказкой – вмурованные кабели должны располагаться вертикально и горизонтально.
Что важно знать о прокладке скрытой проводки в доме или квартире
Если в планах – обновление всей домашней проводки с переустановкой розеток и выключателей, следует заранее ознакомиться с основными правилами ее прокладки. Подробнее об этом рассказывается в специальной статье нашего портала «На какой высоте устанавливать розетки».
Однако, если ясности нет, то придется для начала обнаружить эту «трассу». Для этого используются специальные приборы – детекторы проводки. Кстати, некоторые из них способны сразу показать и тот локальный участок, на котором произошел обрыв фазы. То есть разом решается две задачи.
Понятно, что такие приборы есть далеко не у каждого хозяина. Что ж, можно или приобрести (если это видится доступным по стоимости – он наверняка еще пригодится в будущем), или поискать возможность краткосрочной аренды. Кстати, если уж на какое-то время в руки попал такой прибор – не поленитесь, «просканируйте» все свои жилые владения и составьте схему расположения скрытой проводки – эта информация никогда не будет лишней.
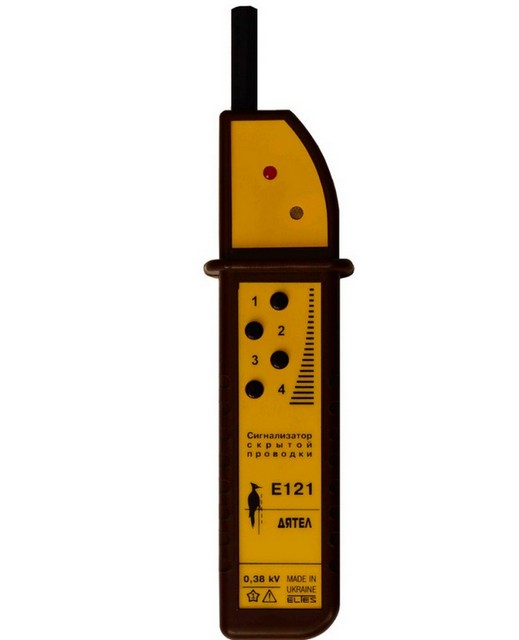
Одним из наиболее популярных среди домашних мастеров является детектор «Eltes Дятел Е121». Прибор способен обнаружить находящуюся под напряжением (и только!) проводку под слоем штукатурки толщиной до 20 мм. Обычно этого бывает достаточно.
Четыре разных порога чувствительности позволяют выявить место прохождения кабеля с довольно высокой точностью. «Дятел» также широко используется и в роли обычного бесконтактного фазного индикатора, например, при проверке правильности подключения проводов в распределительном щите или при выполнении других электромонтажных работ.
Как недостаток – не может точно выявить проводку, расположенную в гильзах или закрытую слоем бетона. Не стоит полагаться на него и при поиске проводки, временно не подключенной к сети – фаза должна быть обязательно.
Видео: Как пользоваться детектором скрытой проводки «Eltes Дятел Е121»
Более совершенными являются приборы, представляющие собой комплект из генератора сигнала и приёмника. С помощью подобного оборудования, подавая на участок срытой проводки, отключённой от сети, сгенерированный сигнал заданной частоты, можно очень точно определить точку обрыва провода.
Ну а в режиме работы без генератора приемник способен определить расположение скрытой проводки, находящейся под напряжением. Типичный пример подобных приборов – отечественный комплект «Лис М» или, более совершенный, «Лис 100».
Видео: Комплект для поиска расположения и дефектов скрытой проводки «Лис М»
Разнообразие детекторов скрытой проводки с возможностью обнаружения дефектных участков в наше время – весьма широкое. Наверное, понятно, что многие из таких устройств позволяют и вовсе обходиться без предварительных этапов поиска участков обрыва – при наличии схемы проводки можно сразу переходить к поиску точки размыкания цепи.
Проблема лишь в том, что качественные приборы с высокой чувствительностью и точностью определения – весьма дорогие. Кроме того, они требуют определенных навыков в работе. И далеко не каждый электрик рискнет дать даже на короткий срок свое оборудование в пользование дилетанту. А так как наша публикация рассчитана именно на начинающих, приходится объяснять простейшие методы диагностики.
Использование подручных или самодельных приборов
Что делать, если нет возможности хотя бы на время обзавестись детектором скрытой проводки?
- При неглубоком залегании кабеля в стене можно попробовать «нащупать» фазу, то есть, при удачном раскладе — и место, где она пропадает (точку обрыва) с помощью обычной индикаторной отвертки. Взяв ее примерно так, как показано на иллюстрации ниже, начинают «сканировать» предполагаемый участок расположения кабеля. Если повезёт, то наличие фазы проявится свечением индикатора. Хотя, если честно, вероятность удачного исследования, скажем так, невысока.
- Более чувствительным, а значит – и более точным может при подобном поиске стать бесконтактный индикатор фазы. Кроме того, он обычно оснащается еще и звуковым сигналом, что облегчает обнаружение скрытого провода. А «технология» поиска – такая же, как и с индикаторной отверткой.
- Встречаются советы – воспользоваться обычным портативным радиоприемником. Его настраивают на частоту примерно в 100 кГц и ведут вдоль стены на предполагаемом участке прохождения кабеля и локализации обрыва. При этом наличие фазы и ее отсутствие должны проявиться наличием и отсутствием явно наводимых помех – шумов.
- Примерно таким же образом – появлением наведенного фона или шумов на фазу может реагировать чувствительный микрофон, подключенный к усилителю (например, старому магнитофону, включенному на режим записи).
- Некоторые пользователи рекомендуют самостоятельно изготовить простейшие детекторы проводки. Набор радиоэлементов требуется совсем небольшой, да и схема сложностью в монтаже не отличается. Вполне можно обойтись даже без изготовления печатной платы.
Вот парочка примеров:
Схема №1
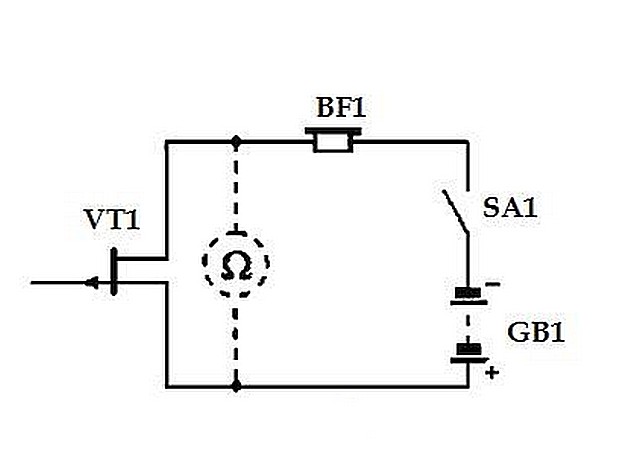
Первую схему можно назвать, пожалуй, самой простой. В элементарную базу входят:
- VT1 – полевой транзистор КП103 (вне зависимости от последующего буквенного обозначения).
- BF1 – акустический индикатор – это может быть динамик, но удобнее использовать наушники.
- SA1 – любой удобный (имеющийся) микровыключатель.
- GB1 – источник питания в качестве, которого достаточно батарейки АА (ААА) напряжением в 1.5 вольта.
В качестве антенны в данном случае может служить сам металлический корпус полевого транзистора. Чем ближе к проводу, в котором имеется фазное напряжение, тем будет громче раздаваться звук в наушниках (частотой около 50 Гц). При определенном старании можно довольно точно обнаружить и месторасположение кабеля, и точку, начиная с которой фаза пропадает.
Схема №2
Этот вариант – несколько понадежней и почувствительней. В нем, кроме полевого транзистора, применено еще и усиление полученного сигнала.
Элементы VT1, BF1, SA1 и GB1 – точно такие же, как и в предыдущей схеме. Кроме того, используются:
VT2 – транзистор, выполняющий роль усилителя. Подойдут КТ3102 или КТ3107 с любыми буквенными индексами.
R1 – резистор 5.1 МОм.
R2 – резистор 3,6 кОм.
Антенной в данном случае выступает отрезок медного провода длиной от 20 до 50 мм. Точность поиска расположения кабеля от этого только выигрывает. А сама «технология» поиска – такая же, как и со схемой №1.
Обратите внимание – все перечисленные способы поиска обрыва рассчитаны на обнаружение фазного напряжения. И, кстати, большинство приборов-детекторов заводской сборки, не оснащенных генераторами сигналов, работают также по этому принципу. То есть, походят для случаев, если обрыв, как показывает предварительная прозвонка участков проводки, был именно на фазном проводе. При этом, конечно, автомат на щитке должен быть включен, и работу, соответственно, следует проводить с соблюдением всех необходимых требований безопасности.
А как быть, или предварительная прозвонка показывает, что повреждён нулевой проводник? Как тогда найти место его обрыва? Ведь прибор попросту не даст ясной картины – он будет реагировать на идущую параллельно фазу.
Поступают таким образом.
- Вначале обесточивают участок.
- Затем вынимают все провода из клемм в щитке, отключают их и на противоположном конце тестируемого участка (в розетке, выключателе или монтажной коробке, если обрыв обнаружен межу нею и щитком). Одним словом, тестируемый участок должен быть гарантировано отключен с обеих сторон.
- Далее, нулевой провод, на котором ищется обрыв, временно подключают со стороны щита к фазному контакту. После этого – включают автомат.
- Производится поиск обрыва по методикам обнаружения фазного напряжения.
- После обнаружения обрыва сразу же, не откладывая (чтобы не забыть!), отключают питание и убирают нулевой провод с фазного контакта.
- После проведения ремонта повреждения все подключается по нормальной схеме.
После того как место обрыва определено, остается заняться ремонтом.
Для этого аккуратно с помощью молотка и зубила, удаляется участок штукатурки, закрывающий проводку. Чтобы не повредить кабель, тем более, если диагностика проводилась приборами со, скажем, не выдающейся точностью, лучше выбирать штрабу с отступом от предполагаемой линии прохождения провода влево – вправо (или вверх – вниз, на горизонтальном участке) на 50 мм. Длина выбираемой штрабы берется такой, чтобы ее было достаточно и для удаления поврежденного участка кабеля, и для зачистки концов с обеих сторон, и для вставки перемычек с их качественным припаиванием (скрутки здесь явно нежелательны), и для последующей надежной изоляции как минимум в два слоя.
Алюминий, конечно, тоже можно паять. Но для этого требуется специальные составы (флюс) и, конечно, умение выполнять подобные соединения. Да и вообще (ИМХО) – от поврежденного участка алюминиевого провода лучше вообще избавиться, заменив его на медь. «Зарывать» же в штукатурку клемму или скрутку — дело весьма рискованное.
Останавливаться на проблемах ремонта поврежденного участка – не станем, так как эта тема все же требует более широкого рассмотрения, и ей лучше уделить внимание в отдельной статье. Но чтобы понятие и о поиске участка аварии, и о ликвидации обрыва стала еще более полным, предлагаем посмотреть интересную видеоподборку, в которой показан один из вариантов выполнения подобных работ.
Видео: Поиск обрыва скрытой проводки и проведение ремонта поврежденного участка
Розетки, лампы, предохранители и прочая электрика соединяются проводами. И часто бывает так, что устройства рабочие, а вот в кабелях идущих между ними случился обрыв. Как его выявить? Проще и дешевле всего использовать мультиметр (пусть даже самый бюджетный). Независимо от того, какие у него параметры, вы сможете проверить любым мультиметром непрерывность цепи 220 В или даже автомобильной проводки по приведённой тут пошаговой инструкции (плюс интересная теория).
Обрыв – это бесконечное сопротивления
Проверка целостности цепи (провода) на самом деле является проверкой сопротивления. Как вы знаете, каждый провод имеет свое собственное электрическое сопротивление, но он очень мало на нескольких (десятках) метрах. Таким образом, если на одной и на другой стороне щупов мультиметра находится один и тот же провод, сопротивление между его клеммами должно быть не более нескольких Ом. В домашних сетях оно обычно ниже 1 Ом.
Когда же сопротивление составляет десятки kΩ (килоом) или MΩ (мегаом), значит либо произошёл разрыв в цепи, либо мы проверяем два разных провода:)
Перед тем как что-нибудь проверять, убедитесь что кабель или провод не под напряжением. Это очень важно, так как в противном случае это будет последнее измерение, проведенное с помощью данного мультиметра. Лучше всего перед проверкой кабель вообще отключить от всего, чтоб удобнее и безопаснее была работа.
Берём мультиметр и включаем щупы
Итак, подходим к ситуации, когда у нас есть оголенные концы проводов с обеих сторон. И теперь перед нами 3 варианта:
- Короткий провод – можно проверить в одном месте с помощью мультиметровых щупов
- Длинный провод – конец провода на большом расстоянии от нас или в двух разных помещениях
- Длинный кабель – только один провод работает на данном участке или много проводов, но мы хотим проверить каждый отдельно.
Начнем с подключения щупов к измерителю. Подключите черный зонд к разъему обозначенному COM, а красный туда, где находится символ сопротивления резистора Ω, поскольку мы фактически проверим сопротивление провода.
Следующий шаг – выбор диапазона. Это символ единицы сопротивления Ω. В данном тестере измерение сопротивления и прозвонка обрыва находятся на одном и том же месте. Поэтому устанавливаем переключатель на эту позицию, а затем используя синюю кнопку выбираем опцию «измерение обрыва», которая подтверждается соответствующим символом в верхней части дисплея.
Если индикатор высветил 0L – это означает, что электрическое сопротивление слишком велико, фактически бесконечно.
В мультиметрах без автоматического выбора диапазона (китайская модель 830) ищем идентичные символы на циферблате. К примеру можно выбрать измерение сопротивления в диапазоне 0-200 Ом. В обоих случаях мы измеряем то же самое, за исключением того, что во время измерения сопротивления мультиметр не сигнализирует звуком низкий уровень сопротивления (замыкание), как это имеет место при измерении непрерывности цепи.
Установка нуля прибора
Перед первым измерением стоит проверить, работает ли мультиметр вообще – это тестируется прижимая наконечники щупов друг к другу.
Устройство должно пикнуть и через некоторое время вы увидите результат измерения сопротивления близкий к 0.0 Ом.
Вы не услышите звуковой сигнал на простых тестерах, но результат измерения будет аналогичен. Теперь начнём проверку обрыва провода в электроцепи.
Короткий кабель – прозвонка
Когда шнур достаточно короткий, чтобы могли достать его оба конца щупами, дело очень простое.
Касаемся одного конца провода одним наконечником, а другого конца провода другим и ожидаем звукового сигнала или результата измерения на дисплее.
Провода могут выгибаться, поэтому надо сжать кончик шнура с щупом пальцами. Но делаем это только в том случае, если чётко проверили что кабель не под напряжением. Мультиметр пищит, сопротивление 0.0 Ом – всё ОК!
Если кабель слишком длинный
Наиболее распространенная ситуация когда концы кабеля расположены в двух удаленных местах. Что делать?
С одной стороны соединяем два провода одного жгута, например используя электрический монтажный блок, или просто скручиваем их вместе.
После этой операции с другой стороны, если провод не обрывается в какой-либо точке, сопротивление между проводами должно быть незначительным из-за прямого подключения этих жил.
Проверка одного длинного провода
А если нужно проверить только одну жилу? Это можно сделать так. Например есть 2-х проводный кабель, и интересует, оборвана ли только одна линия, и если да, то какая.
В основном вы должны делать то же, что и в предыдущем этапе, только с использованием дополнительного провода с любым поперечным сечением.
Берем дополнительный шнур и с одной стороны прикручиваем его к проводу, который хотим исследовать. Ведем его ко второму месту, где расположен второй конец провода.
Касаемся щупами и измеряем. Если всё хорошо, будет результат измерения близко к 0 Ом, если что-то пойдет не так, измерение будет несколько kΩ, MΩ или даже на дисплее будет просто 0L – обрыв.
Выводы и рекомендации
- Всегда проводим измерения сопротивления в свободном состоянии тестируемых проводников. Измерение провода под напряжением является летальным. По крайней мере для мультиметра.
- Измерение цепи на самом деле является проверкой её электрического сопротивления.
- Когда проводник не поврежден, результат измерения должен быть не более нескольких Ом.
- Прежде чем выполнять само измерение на обрыв, стоит выполнить пробное измерение на щупах, чтобы проверить рабочий ли прибор.
Проверка обрыва проводки в авто производится аналогично, с той лишь разницей, что можно не опасаться удара тока 220 В в виду отсутствия такового (это не относится к электромобилям – там бывает и 600!).
Содержание
- 2 Схемы
- Проверка обрыва провода в цепи мультиметром
- Обрыв – это бесконечное сопротивления
- Берём мультиметр и включаем щупы
- Установка нуля прибора
- Короткий кабель – прозвонка
- Если кабель слишком длинный
- Проверка одного длинного провода
- Выводы и рекомендации
- Как прозвонить провода мультиметром
- Что нужно знать о приборе, чтобы прозванивать провода
- Последовательность действий при прозвонке
- Правила безопасной прозвонки с использованием мультиметра
- Прозваниваем проводку в квартире мультиметром
- Если автоматы не сработали
- Если автомат сработал
- Видео
2 Схемы
Принципиальные электросхемы, подключение устройств и распиновка разъёмов
Проверка обрыва провода в цепи мультиметром

Розетки, лампы, предохранители и прочая электрика соединяются проводами. И часто бывает так, что устройства рабочие, а вот в кабелях идущих между ними случился обрыв. Как его выявить? Проще и дешевле всего использовать мультиметр (пусть даже самый бюджетный). Независимо от того, какие у него параметры, вы сможете проверить любым мультиметром непрерывность цепи 220 В или даже автомобильной проводки по приведённой тут пошаговой инструкции (плюс интересная теория).
Обрыв – это бесконечное сопротивления
Проверка целостности цепи (провода) на самом деле является проверкой сопротивления. Как вы знаете, каждый провод имеет свое собственное электрическое сопротивление, но он очень мало на нескольких (десятках) метрах. Таким образом, если на одной и на другой стороне щупов мультиметра находится один и тот же провод, сопротивление между его клеммами должно быть не более нескольких Ом. В домашних сетях оно обычно ниже 1 Ом.
Когда же сопротивление составляет десятки kΩ (килоом) или MΩ (мегаом), значит либо произошёл разрыв в цепи, либо мы проверяем два разных провода:)
Перед тем как что-нибудь проверять, убедитесь что кабель или провод не под напряжением. Это очень важно, так как в противном случае это будет последнее измерение, проведенное с помощью данного мультиметра. Лучше всего перед проверкой кабель вообще отключить от всего, чтоб удобнее и безопаснее была работа.
Берём мультиметр и включаем щупы
Итак, подходим к ситуации, когда у нас есть оголенные концы проводов с обеих сторон. И теперь перед нами 3 варианта:
- Короткий провод – можно проверить в одном месте с помощью мультиметровых щупов
- Длинный провод – конец провода на большом расстоянии от нас или в двух разных помещениях
- Длинный кабель – только один провод работает на данном участке или много проводов, но мы хотим проверить каждый отдельно.
Начнем с подключения щупов к измерителю. Подключите черный зонд к разъему обозначенному COM, а красный туда, где находится символ сопротивления резистора Ω, поскольку мы фактически проверим сопротивление провода.
Следующий шаг – выбор диапазона. Это символ единицы сопротивления Ω. В данном тестере измерение сопротивления и прозвонка обрыва находятся на одном и том же месте. Поэтому устанавливаем переключатель на эту позицию, а затем используя синюю кнопку выбираем опцию «измерение обрыва», которая подтверждается соответствующим символом в верхней части дисплея.
Если индикатор высветил 0L – это означает, что электрическое сопротивление слишком велико, фактически бесконечно.
В мультиметрах без автоматического выбора диапазона (китайская модель 830) ищем идентичные символы на циферблате. К примеру можно выбрать измерение сопротивления в диапазоне 0-200 Ом. В обоих случаях мы измеряем то же самое, за исключением того, что во время измерения сопротивления мультиметр не сигнализирует звуком низкий уровень сопротивления (замыкание), как это имеет место при измерении непрерывности цепи.
Установка нуля прибора
Перед первым измерением стоит проверить, работает ли мультиметр вообще – это тестируется прижимая наконечники щупов друг к другу.
Устройство должно пикнуть и через некоторое время вы увидите результат измерения сопротивления близкий к 0.0 Ом.
Вы не услышите звуковой сигнал на простых тестерах, но результат измерения будет аналогичен. Теперь начнём проверку обрыва провода в электроцепи.
Короткий кабель – прозвонка
Когда шнур достаточно короткий, чтобы могли достать его оба конца щупами, дело очень простое.
Касаемся одного конца провода одним наконечником, а другого конца провода другим и ожидаем звукового сигнала или результата измерения на дисплее.
Провода могут выгибаться, поэтому надо сжать кончик шнура с щупом пальцами. Но делаем это только в том случае, если чётко проверили что кабель не под напряжением. Мультиметр пищит, сопротивление 0.0 Ом – всё ОК!
Если кабель слишком длинный
Наиболее распространенная ситуация когда концы кабеля расположены в двух удаленных местах. Что делать?
С одной стороны соединяем два провода одного жгута, например используя электрический монтажный блок, или просто скручиваем их вместе.
После этой операции с другой стороны, если провод не обрывается в какой-либо точке, сопротивление между проводами должно быть незначительным из-за прямого подключения этих жил.
Проверка одного длинного провода
А если нужно проверить только одну жилу? Это можно сделать так. Например есть 2-х проводный кабель, и интересует, оборвана ли только одна линия, и если да, то какая.
В основном вы должны делать то же, что и в предыдущем этапе, только с использованием дополнительного провода с любым поперечным сечением.
Берем дополнительный шнур и с одной стороны прикручиваем его к проводу, который хотим исследовать. Ведем его ко второму месту, где расположен второй конец провода.
Касаемся щупами и измеряем. Если всё хорошо, будет результат измерения близко к 0 Ом, если что-то пойдет не так, измерение будет несколько kΩ, MΩ или даже на дисплее будет просто 0L – обрыв.
Выводы и рекомендации
- Всегда проводим измерения сопротивления в свободном состоянии тестируемых проводников. Измерение провода под напряжением является летальным. По крайней мере для мультиметра.
- Измерение цепи на самом деле является проверкой её электрического сопротивления.
- Когда проводник не поврежден, результат измерения должен быть не более нескольких Ом.
- Прежде чем выполнять само измерение на обрыв, стоит выполнить пробное измерение на щупах, чтобы проверить рабочий ли прибор.
Проверка обрыва проводки в авто производится аналогично, с той лишь разницей, что можно не опасаться удара тока 220 В в виду отсутствия такового (это не относится к электромобилям – там бывает и 600!).
Источник
Как прозвонить провода мультиметром
Если нужно найти неисправность оборудования или электрической проводки, одной из операций, которая выполняется в первую очередь, является прозвонка кабелей и проводов мультиметром (тестером) для проверки исправности цепи (отсутствия в ней разрывов), наличия короткого замыкания и определения её сопротивления (если это необходимо). Таким образом удаётся легко и достаточно быстро проверить на исправность лампу, утюг, выключатель, предохранитель, трансформатор. О том, как прозвонить провода мультиметром правильно, и пойдёт речь в этой статье.
Что нужно знать о приборе, чтобы прозванивать провода
Если вы планируете прозвонить проводку в квартире, нужно знать о мультиметрах несколько принципиально важных фактов. В первую очередь стоит отметить, что проверить провод можно самым простым прибором. Вполне подойдёт недорогая китайская модель с минимальными возможностями.
Но при этом удобнее всего использовать устройство, в котором есть сама функция прозвонки. Для того чтобы установить ручку прибора в соответствующее положение, необходимо повернуть её в направлении значка диода (как вариант, дополнительно может быть нанесено изображение звуковой волны). Это означает, что при проверке целостности провода при замыкании контактов прозвучит звуковой сигнал.
Но наличие звукового сопровождения совершенно необязательно для прозвонки проводов мультиметром. О том, что цепь разорвана, будет свидетельствовать единица на дисплее, показывающая, что уровень сопротивления между щупами выше, чем предел измерений. Если же на исследуемом участке повреждений нет, на экран будет выведено значение сопротивления, которое в идеале должно стремиться к нулю (при условии работы в бытовых сетях небольшой протяжённости).
Последовательность действий при прозвонке
- Перед тем, как прозвонить цепь мультиметром, нужно повернуть ручку прибора в нужное положение.
- Установить концы (измерительные провода) в соответствующие гнёзда. Чёрный провод в гнездо, обозначенное СОМ (иногда оно может быть обозначено «*» или знаком заземления), а красный – в гнездо, где указан знак Ω (иногда ставят знак R). Стоит отметить, что знак Ω может быть нанесён как отдельно, так и в сочетании с обозначениями других единиц измерения (V, mA). Это правильное положение измерительных проводов, которое позволит соблюдать полярность при проведении дальнейших измерений. Хотя если будет проверяться только целостность проводов, взаимное положение их на полученный результат никак не повлияет.
- Включить прибор. Для этого может быть предусмотрена отдельная кнопка или включение может происходить автоматически при повороте ручки в нужное положение при выборе пределов измерения или режима работ.
- Замкнуть измерительные концы между собой. Если прозвучит сигнал, значит, прибор исправен и готов к работе.
- Взять проверяемый кабель или провод (предварительно его концы должны быть оголены от изоляции, зачищены до металлического блеска, удалена с поверхности грязь, окислы). Прикоснуться измерительными проводами к оголённым участкам проводника.
- В случае целостности прозвучит сигнал, а показания прибора будут или равны 0, или укажут на значение сопротивления. Если на дисплее будет отображена 1 и не будет звукового сигнала, это означает, что проверенный проводник оборван.
Правила безопасной прозвонки с использованием мультиметра
Работа с электричеством не допускает непрофессионализма, поэтому сложился определённый перечень правил, которые позволяют сделать её максимально точной, быстрой и безопасной.
- Удобнее всего при прозвонке использовать на концах измерительных проводов специальные наконечники, которые получили более распространённое название «крокодилы». Они позволят сделать контакт устойчивым и освободят руки при проведении измерений.
- При прозвонке всегда проверяемая цепь должна быть предварительно обесточена (необходимо удалить даже слаботочные батарейки). Если в цепи стоят конденсаторы, они должны быть разряжены закорачиванием. В противном случае при проведении работ прибор просто сгорит.
- Перед тем как проверить целостность проводника большой длины при проведении измерений важно не прикасаться руками к его оголённым концам. Это связано с тем, что полученные в результате показания могут быть некорректны.
При прозвонке многожильного кабеля необходимо с обоих концов разделить и зачистить все имеющиеся жилы. После этого нужно проверить цепь на наличие в ней коротких замыканий: для этого на каждой жиле поочерёдно закрепляется «крокодил», ко всем оставшимся прикасаются другим измерительным концом во всех возможных комбинациях.
В данном случае звуковой сигнал будет означать наличие между проверяемыми жилами короткого замыкания. Это может не иметь практического значения для многожильных кабелей малого сечения, работающих в слаботочных сетях, но при работе с высоким напряжением это принципиально важно.
Чтобы определить целостность жил выполняется та же операция, только на одном из концов кабеля все зачищенные жилы скручиваются вместе. При поиске обрыва важно учитывать, что отсутствие на каком-либо из концов звукового сигнала будет говорить о нарушении целостности проводника.
Прозваниваем проводку в квартире мультиметром
Рассмотрим в качестве примера современную квартиру, в которой проводка выполнена в соответствии с действующими требованиями и нормами. Это значит, что при прокладке линии освещения и питания розеток были разведены, и в каждую из комнат для них проложены отдельные провода. Каждая из таких цепей питается от квартирного щитка через отдельный автоматический выключатель.
Если в одной из комнат исчез свет, для начала стоит проверить исправность светильника. Перед началом работ необходимо обесточить комнату/квартиру в зависимости от схемы питания. При использовании в светильнике непрозрачной лампы накаливания, целостность нити визуально определить сложно, поэтому потребуется мультиметр и его функция прозвонки. Давайте поэтапно разберёмся, как правильно это сделать.
Вначале нужно проверить щиток на наличие сработавших автоматов. В первом случае они будут находиться во включенном положении (тогда неисправность может скрываться в комнатном выключателе, лампе или патроне). Вероятность повреждения проводки в такой ситуации мала. Если же аппарат сработал, нужно будет проверять всё кроме комнатного выключателя, включая сам щитовой автомат.
Если автоматы не сработали
- Убедиться в наличии напряжения на входе и выходе автомата. Если оно есть, можно переходить к дальнейшей проверке.
- Подготовить прибор к работе и проверить его исправность закорачиванием измерительных концов.
- Выкрутить из патрона лампу.
- Одним из измерительных щупов коснуться цоколя (металлической части лампы с резьбой), а вторым – центрального контакта лампы (изолированного центра торцевой части цоколя).
- Звуковой сигнал и показания прибора, которые отличны от 0 или 1, означают, что лампа исправна. Если неисправна, нужно её заменить, что и станет решением проблемы.
- Проверяем на исправность патрон. Для этого нужно разобрать светильник, убедиться в целостности подведенных проводов, контактов. Если всё в порядке, то причина поломки не в патроне. При обнаружении неисправностей их нужно устранить. Лампу пока вкручивать нельзя.
- Проверяем исправность комнатного выключателя. Для этого снимаем пластиковую накладку, откручиваем винты и достаём его из монтажной коробки. Осматриваем оборудование на предмет появления нагара, проверяем затяжку креплений. Если всё исправно, нужно измерительные концы тестера установить на контакты выключателя. Появление звукового сигнала при прозвонке во включенном положении будет свидетельствовать о том, что оборудование исправно. Провода при этом можно не отсоединять.
В ходе такой проверки, как правило, выявляется неисправность, которая и становится причиной всех неприятностей. Её устранение позволяет быстро решить проблему.
Если автомат сработал
Для обеспечения электробезопасности при проведении работ в этом случае напряжение отключается при помощи общеквартирного автомата. Далее определяется исправность патрона и подведенных к светильнику проводов по алгоритму, описанному выше. При отсутствии неисправностей, нужно проверить саму проводку, используя мультиметр и функцию прозвонки. Такие неисправности случаются достаточно редко, но всё же бывают, к примеру, при установке подвесных потолков или декоративных элементов интерьера.
Прозвонка проводки в этом случае выполняется следующим образом.
- С помощью отвёртки отключаем подведенный проводник (при правильно выполненном монтаже он находится снизу) и отводим его в сторону. «Ноль» этой группы находится, как правило, на нулевом зажиме под автоматами.
- Выкручиваем из патрона лампу накаливания. При помощи готового к работе тестера проверяем линию, подключаясь одним из измерительных щупов к «нулю», а другим – к отсоединённому проводнику. Если прибор подаёт звуковой сигнал, значит, проводка закорочена.
- В этом случае в комнате под потолком вверху над выключателем находим и вскрываем соединительную коробку. Рассоединяем провода.
- Проверяем все группы проводов на наличие в них короткого замыкания.
Для определения участка цепи, в котором имеется короткое замыкание, снова проверяем мультиметром цепи на квартирном щитке. Если сигнал прозвучит, значит, ремонту подлежит именно провод, проложенный от щита до коробки в комнате. В противном случае, поиски нужно будет продолжить до получения результата.
Видео
Из всего вышеизложенного можно сделать вывод о том, что наличие в доме мультиметра с функцией прозвонки – объективная необходимость для любого домашнего мастера. С таким прибором в большинстве случаев можно будет быстро устранить мелкие неисправности, не обращаясь за помощью к специалистам.
Источник
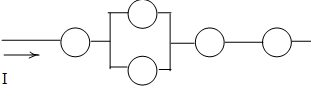
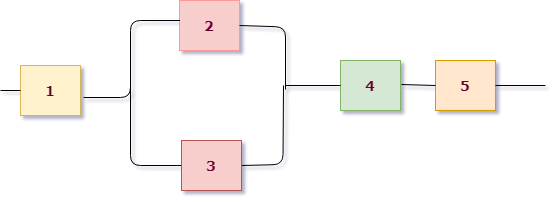
Что такое электрическая цепь?
Вы, возможно, задавались вопросом, как заряды могут непрерывно течь в одном направлении по проводам без использования гипотетических источников и пунктов назначения. Чтобы схема с источником и пунктом назначения работала, они оба, чтобы поддерживать непрерывный поток, должны иметь бесконечную емкость для зарядов!
Используя аналогию с шариками и трубкой из предыдущей статьи о проводниках, диэлектриках и потоке электронов, источник шариков и приемное ведро для шариков должны быть бесконечно большими, чтобы вместить достаточно шариков для поддержания «потока».
Что такое электрическая цепь?
Ответ на этот парадокс можно найти в концепции электрической цепи: бесконечный петлевой путь для носителей заряда. Если мы возьмем провод или несколько проводов, соединенных встык, и закрутим его так, чтобы он образовал непрерывный путь, у нас будут средства для поддержания направленного потока заряда, не прибегая к бесконечным источникам и приемникам:
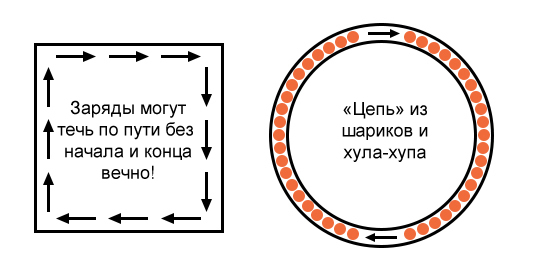
Каждый носитель заряда, движущийся по часовой стрелке в этой цепи, толкает того, что находится перед ним, который толкает того, что находится перед ним, и так далее, и так далее, точно так же, как хула-хуп, наполненный шариками. Теперь у нас есть возможность поддерживать непрерывный поток заряда бесконечно без необходимости бесконечных источников и приемников. Всё, что нам нужно для поддержания этого потока, – это средства непрерывного побуждения этих носителей заряда, о которых мы поговорим в следующем разделе этой главы, посвященном напряжению и току.
Что означает обрыв цепи?
Целостность в цепи так же важна, как и в простом куске провода. Как и в примере с простым отрезком провода между источником и приемником, любой разрыв в этой цепи помешает прохождению через нее заряда:
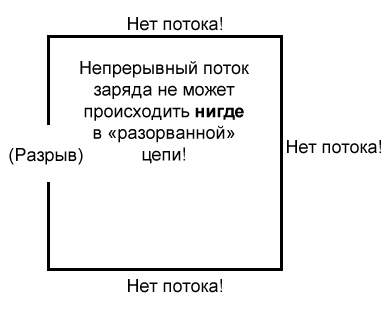
Здесь важно понимать, что не имеет значения, где происходит разрыв. Любое нарушение целостности в цепи остановит поток заряда по всей цепи. Если не существует целой, безразрывной петли из проводящего материала, через которую проходят носители заряда, устойчивый поток просто не может поддерживаться.
Источник
Обрыв и короткое замыкание в чём разница?
Обрыв и короткое замыкание — это два явления в электрических цепях, которые заслуживают особого внимания при изучении основ электротехники. Ниже приведены 5 различий между разомкнутыми и короткими замыканиями.
Какое отличие между обрывом и коротким замыканием в электрике?
Ток, проходящий через разомкнутую цепь, равен нулю, в то время как ток через короткое замыкание бесконечен.
Разомкнутая цепь обладает бесконечным сопротивлением, в то время как короткое замыкание обладает нулевым сопротивлением.
Напряжение через короткое замыкание равно нулю, а напряжение через короткое замыкание-максимуму.
Омметр, подключенный к короткому замыканию, показывает «0» Ом, а омметр, подключенный к разомкнутой цепи, показывает «бесконечность» или «0L».
Практически короткое замыкание происходит, когда провода с различными значениями потенциала соединяется между собой, а разомкнутая цепь возникает, когда цепь разрывается с какой-то точки.
Основные определения обрыва и короткого замыкания
Разомкнутая цепь (обрыв) — это цепь, имеющая разъединение между компонентами. На рисунке ниже показан разрыв цепи:
Короткое замыкание — это когда компоненты электрической цепи соединены с очень малым или нулевым сопротивлением провода. На рисунке ниже показано идеальное короткое замыкание:
Сопротивление
Разомкнутая цепь обладает бесконечным сопротивлением, в то время как короткое замыкание обладает нулевым сопротивлением.
Ω для открытого → бесконечного
Омметр, подключенный через короткое замыкание, показывает «0» Ом или очень малые значения ом. Омметр через разрыв будет отображать «1» или «0L». Большинство производителей мультиметров показывают «0L» для открытого.
Чтобы обезопасить от поражения электрическим током человека, а также безопасного применения электрических приборов, используют различные виды защитных элементов.
Источник
Переходные процессы в электрических цепях
Переходные процессы в электрических цепях:
Переходный процесс в электрической цепи — это электромагнитный процесс, возникающий в электрической цепи при переходе от одного установившегося (принужденного) режима к другому. Установившимся (принужденным) называется режим работы электрической цепи, при котором напряжение и токи цепи в течение длительного времени остаются неизменными.
Такой режим в электрической цепи устанавливается при длительном действии источников постоянной или переменной ЭДС при неизменных параметрах этой цепи R, L и С.
Переходный процесс вызывается коммутацией в цепи. Коммутацией называется процесс замыкания или размыкания рубильников или выключателей. Переходный процесс может быть вызван изменением параметров электрической цепи R, L или С.
Переходный процесс базируется на двух законах коммутации:
- ток в индуктивности не может изменяться скачком;
- напряжение на емкости не может изменяться скачком.
Действительно, если ток в индуктивности L изменяется скачком, т. е. мгновенно, то ЭДС самоиндукции eL становится бесконечно большой (при
В реальных цепях ЭДС самоиндукции может иметь только конечные значения.
Если в цепи с емкостью С напряжение на ее обкладках изменяется скачком, т. е. мгновенно, то появляется бесконечно большой зарядный (или разрядный) ток (при 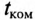
Ток в электрических цепях может иметь только конечные значения.
Переходный процесс является быстропротекающим процессом, длительность которого обычно составляет десятые, сотые и даже миллионные доли секунды и сравнительно редко — секунды и даже десятки секунд.
Таким образом, один установившийся режим цепи отделяется от другого некоторым промежутком времени, в течение которого происходит постепенный переход от прежнего состояния цепи к новому.
Переходный процесс в линейных цепях можно рассматривать как результат наложения двух процессов:
- нового установившегося режима, который наступает после коммутации;
- свободного процесса, обеспечивающего переход цепи от прежнего установившегося режима к новому установившемуся режиму.
Таким образом, ток i цепи в течение переходного процесса можно представить суммой двух токов: нового установившегося 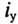
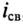
Аналогично напряжение в течение переходного процесса равно
В результате переходного процесса происходят изменения тока, напряжения, фазы, частоты и т.д.
Изучение переходных процессов очень важно, так как оно позволяет выявить возможные превышения напряжения на отдельных участках цепи, которые могут оказаться опасными для изоляции установки, позволяет выявить возможные броски токов, величина которых в десятки раз превышает установившийся. Изучение переходных процессов позволяет выявить ситуации, возникающие в электрических цепях при коротком замыкании, резком включении и выключении рубильников, и прочие режимы работы цепи.
Переходный процесс в электрической цепи
Переходный процесс в электрической цепи — это процесс, возникающий в электрической цепи при различных воздействиях, приводящих их из стационарного состояния в новое стационарное состояние, когда при действии различного рода коммутационной аппаратуры, например, ключей, переключателей для включения или отключения источника или приёмника энергии, при обрывах в цепи, при коротких замыканиях отдельных участков цепи и т. д.
Подключение катушки индуктивности к источнику с постоянным напряжением
Если катушку индуктивности (RL) подключить к источнику с постоянным напряжением U (замыкание ключа К), то ток i в не-разветвленной цепи (рис. 20.1а) будет увеличиваться от нуля (в начале переходного процесса) до установившегося значения
Установившийся, т.е. постоянный, ток I не индуктирует в катушке ЭДС самоиндукции, поэтому индуктивное сопротивление в установившемся режиме при условии (20.3) отсутствует.
Этот увеличивающийся ток i индуктирует в индуктивности L катушки ЭДС самоиндукции (см. (9.11))
Следовательно, для любого момента времени переходного процесса по второму закону Кирхгофа можно записать
Разделив уравнение (20.4) на R, получают
В уравнении (20.5) 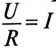
Отношение — 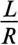
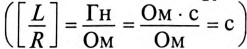
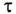
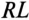
Тогда уравнение (20.5) можно записать в виде
Если это уравнение проинтегрировать, предварительно разделив переменные (ток и время), а затем спотенцировать, то получим выражение
где е — основание натурального логарифма (е=2,71); I — установившийся ток (
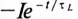
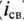
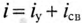
Таким образом, уравнение, которое позволяет определить вели-шу тока в цепи с индуктивностью L в любой момент переходно-процесса RL-цепи при подключении реальной катушки индук-1Вности к источнику с постоянным напряжением U, записывается в виде
Воспользовавшись Приложением 9, по выражению (20.10) можно определить, что за время t= 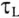
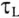
Теоретически переходный процесс происходит бесконечно долго. Практически переходный процесс в рассматриваемой цепи считается законченным, когда ток i увеличивается до 99 % установившегося тока I.
Как видим, чем больше xL, тем больше времени t длится перечный процесс.
Таким образом, постоянная времени xL определяет скорость греховного процесса или его длительность.
ЭДС самоиндукции в рассматриваемой цепи, вызванная свободным током 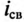
Таким образом, ЭДС самоиндукции в 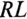
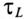
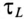
Увеличение тока и уменьшение ЭДС самоиндукции катушки при подключении катушки к источнику с постоянным напряжением U показаны на графике рис. 20.1б.
Отключение и замыкание RL-цепи
Если цепь с катушкой, в которой проходит установившийся ток I (рис. 20.1а), разомкнуть, то ток i в такой цепи с большой скоростью уменьшается до нуля и в катушке индуктируется большая ЭДС самоиндукции eL
Эта ЭДС полностью приложена к клеммам ключа, так как при размыкании сопротивление ключа становится бесконечно большим. Эта ЭДС вызывает значительное увеличение электрического поля между контактами ключа, а следовательно, и напряженности поля. Большая напряженность электрического поля может вызвать искровой и даже дуговой разряд между размыкающимися контактами ключа, в результате чего обгорают контакты ключа.
Поэтому рубильники в RL-цепях шунтируются специальными устройствами, которые обеспечивают гашение дугового разряда. Для гашения дугового разряда необходимо одновременно с отключением катушки индуктивности от источника замкнуть ее на разрядное сопротивление R0 (рис. 20.2а).
Уменьшение тока 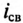
Наглядно это уменьшение можно наблюдать на рис. 20.1б, если кривую изменения eL считать кривой уменьшения тока 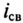
Постоянная времени при отключении катушки от источника с постоянным напряжением U определяется как и при включении катушки на это напряжение, т.е.
Если катушку с установившимся током I, зашунтированную сопротивлением Ro (рис. 20.2а), отключить от источника (разомкнуть ключ К), то в замкнутом контуре ABCD в начальный момент коммутации 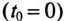
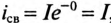
Для определения активного сопротивления катушки 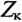
Как видно, за счет переходных процессов в цепях с индуктивностью возникают большие токи и напряжения. С этим необходимо считаться и учитывать при проектировании и эксплуатации цепей с индуктивностью.
Зарядка, разрядка и саморазрядка конденсатора
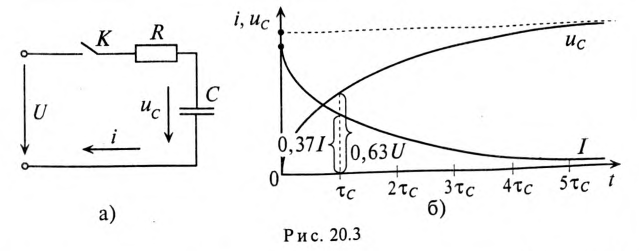
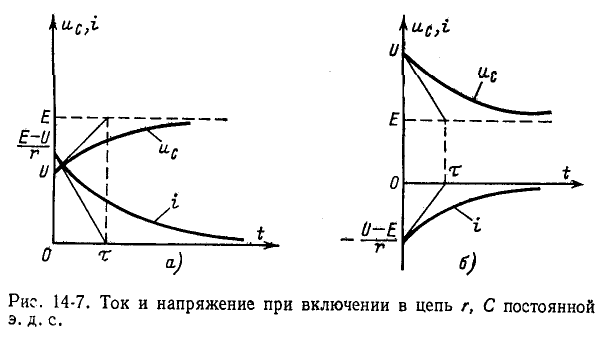
Если конденсатор с сопротивлением (утечки) R и емкостью С подключить к источнику с постоянным напряжением U (замыканием ключа К), то в цепи (рис. 20.3а) появится ток зарядки конденсатора (см. (11.16)):
где 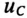
По второму закону Кирхгофа для цепи зарядки конденсатора (рис. 20.3а) можно записать уравнение
где произведение RC имеет размерность времени, обозначается буквой 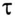
Уравнение (20.13) можно записать в виде
Если в уравнении (20.15) разделить переменные, проинтегрировать, а затем спотенцировать, то получится выражение
где U — установившееся напряжение 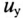
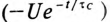
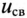
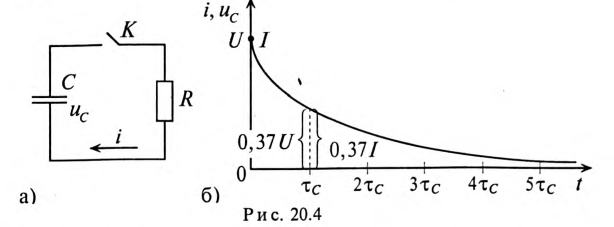
Следовательно, напряжение на заряжающемся конденсаторе в любой момент времени t переходного процесса определяется выражением
По (20.17), пользуясь Приложением 9, можно определить, что за время t= 
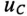

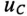
Теоретически зарядка конденсатора длится бесконечно долю а практически конденсатор считается заряженным, когда напряжение на нем достигает 99 % напряжения источника U.
Таким образом, и в RC-цепи, чем больше постоянная времени 

Ток i при зарядке конденсатора (см. (20.13)) уменьшается по за кону
(20. IS)
где 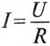
За время t= 

Графики изменения напряжения на конденсаторе и тока в цепи арядки конденсатора изображены на рис. 20.36.
Если конденсатор емкостью С, заряженный предварительно до напряжения U, разряжать через резистор с сопротивлением R рис. 20.4а), то напряжение 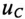
где U — напряжение на конденсаторе до начала разрядки (при t= 0), а 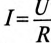

За время t= 
Если конденсатор емкостью С, заряженный до напряжения U, отсоединить от источника, то он будет разряжаться через свой диэлектрик. Напряжение на нем будет уменьшаться по закону 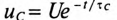
Постоянная времени саморазряда зависит от физических свойств диэлектрика
где р — удельное сопротивление диэлектрика; 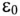
Для определения напряжения, тока, ЭДС в любой момент переходного процесса 
Катушка электромагнита с параметрами 
Установившийся ток
Постоянная времени для катушки
Подставляем значение величин в (20.10):
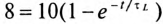
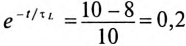
По Приложению 9 определяется 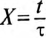
ЭДС самоиндукции за время 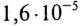
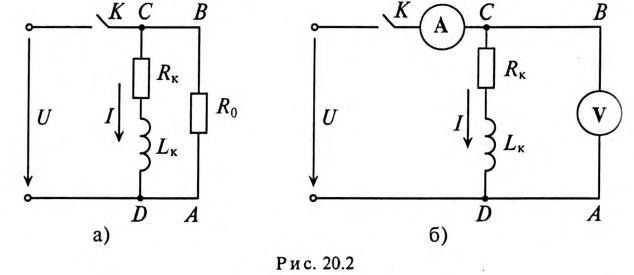
К зажимам катушки индуктивности с параметрами 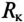
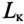
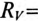
Определить напряжение на зажимах вольтметра и ток в обмотках прибора (обмотки соединены последовательно) при t=0, если размыкание рубильника К произойдет мгновенно и дуги не возникнет.
До размыкания рубильника через катушку проходил ток
В момент размыкания рубильника (t = 0) весь этот ток проходит обмоткам вольтметра. При этом на вольтметре напряжение cтанет равным
Такого напряжения (10 кВ) и такого тока (2 А) обмотка вольтметра (обычно подвижная обмотка электродинамического прибора рассчитана на ток порядка десятков, максимум, сотен миллиампер) не выдержит и сгорит.
При размыкании рубильника с конечной скоростью между расходящимися контактами рубильника К (рис. 20.26) возникнет электрическая дуга. Это приведет к тому, что увеличение напряжения на вольтметре и тока через обмотки вольтметра будет меньше, чем в рассмотренном выше случае (мгновенное размыкание рубильника). Однако меры предосторожности для сохранения вольтметра и рубильника, описанные выше, нужно соблюдать.
Конденсатор емкостью С= 2 мкФ через сопротивление R= 500 кОм подключается к источнику с постоянным напряжением U= 220 В.
Определить напряжение на конденсаторе 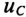
Постоянная времени заряда конденсатора
Напряжение на конденсаторе через 2 с от начала заряда
Ток в цепи заряда конденсатора через 2 с от начала заряда
так как
Время t’ заряда конденсатора до напряжения 150 В определяется по формуле (20.17):
Откуда
Из таблицы показательных функций (Приложение 9) находят t’= 1,14 с.
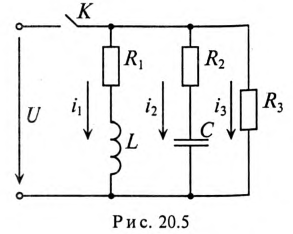
Параметры цепи, изображенной на рис. 20.5, следующие:
Определить значение токов в ветвях через время t= 2 с после замыкания ключа К.
Для ветви (1) с индуктивностью определяются:
установившийся ток
и постоянная времени
Тогда ток через 2 с будет равен
Для ветви (2) с емкостью определяются:
максимальный установившийся ток по окончании переходного процесса
и постоянная времени 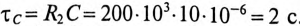
Тогда ток зарядки через 2 с будет равен
Для ветви (3) с активным сопротивлением 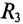
Постоянная времени 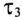
Через 2 с значение тока будет таким же, т. е.
Переходные процессы в электрических цепях. Классический метод расчета
Возникновение переходных процессов:
В предыдущих главах рассматривались установившиеся процессы в линейных электрических цепях, т. е. такие процессы, при которых напряжения и токи либо неизменны во времени (цепи постоянного тока), либо представляют собой периодические функции времени (цепи переменного тока).
Наступлению установившегося процесса, отличного от первоначального режима работы цепи, предшествует, как правило, переходный процесс, при котором напряжения и токи изменяются непериодически.
Переход от одного режима работы цепи к другому может быть вызван изменением параметров или схемы цепи, называемым в общем случае в электротехнике коммутацией.
Можно теоретически считать, что коммутация цепи производится мгновенно, т. е. на включение, выключение или переключение цепи время не расходуется. Тем не менее переход от исходного режима работы цепи к последующему установившемуся процессу происходит не мгновенно, а в течение некоторого времени. Объясняется это тем, что каждому состоянию цепи соответствует определенный запас энергии электрических и магнитных полей. Переход к новому режиму связан с нарастанием или убыванием энергии этих полей. Энергия 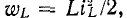
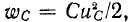
Если исключить случаи размыкания индуктивности и замыкания накоротко емкости и рассматривать цепи, в которых энергия, накапливаемая в магнитном или электрическом поле, может рассеиваться в виде теплоты в сопротивлениях, то, считая, что коммутация происходит мгновенно, можно искрообразование не учитывать.
Для завершения переходного и наступления установившегося процессов теоретически требуется бесконечно большое время. Практически, однако, время переходного процесса определяется малым интервалом, по истечении которого токи и напряжения настолько приближаются к установившимся значениям, что разница оказывается практически неощутимой. Чем интенсивнее происходит рассеяние энергии в сопротивлениях, тем быстрее протекает переходный процесс.
Если бы электрическая цепь состояла только из сопротивлений и не содержала индуктивностей и емкостей, то переход от одного установившегося состояния к другому совершался бы мгновенно, без затраты времени. В реальных электротехнических устройствах тепловые потери, обусловленные током, магнитные и электрические поля сопутствуют друг другу. Применяя специальные схемы и подбирая соответствующие параметры цепи, можно в зависимости от необходимости ускорить или замедлить переходный процесс.
В одних случаях переходные процессы в электрических цепях нежелательны и опасны (например, при коротких замыканиях в энергетических системах). В других случаях переходный процесс представляет собой естественный, нормальный режим работы цепи, как это, например, имеет место в радиопередающих и радиоприемных устройствах, системах автоматического регулирования и других цепях.
Существуют различные методы расчета переходных процессов в линейных электрических цепях. Настоящая глава посвящена классическому методу решения дифференциальных уравнений, описывающих переходные процессы.
Законы коммутации и начальные условия
Высказанные выше положения о том, что запас энергии магнитного или электрического поля может изменяться только плавно, без скачков, выражают принцип непрерывности во времени потокосцепления индуктивности и электрического заряда емкости и называются законами коммутации.
Невозможность скачкообразного изменения потокосцепления следует из того, что в противном случае на индуктивности появилось бы бесконечно большое напряжение 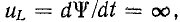
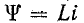
Аналогично невозможность скачкообразного изменения электрического заряда q следует из того, что в противном случае через емкость проходил бы бесконечно большой ток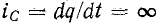
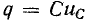
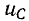
При этом следует отметить, что в цепях с идеализированными сосредоточенными параметрами скачкообразно могут изменяться: 1) токи в сопротивлениях и емкостях и 2) напряжения на сопротивлениях и индуктивностях.
Значения тока в индуктивности и напряжения на емкости в момент коммутации называются независимыми начальными условиями.
Обычно принимают, что коммутация происходит в момент времени t= 0; тогда ток в индуктивности и напряжение на емкости в момент времени непосредственно перед коммутацией обозначаются через 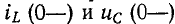
На основании законов коммутации: 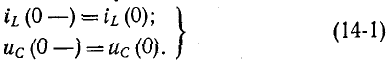
Эти равенства выражают начальные условия цепи, в которых происходит коммутация.
При нулевых начальных условиях, т. е. косца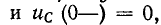
В случае ненулевых начальных условий, т. е. когда 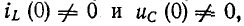
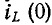
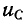
Независимые начальные условия характеризуют энергию магнитного и электрического полей, запасенную к моменту коммутации, и для расчета переходного процесса обязательно требуется знание этих начальных условий, причем совершенно безразлично, каким образом эти условия в цепи были созданы.
При расчете переходных процессов в разветвленных электрических цепях наряду с независимыми начальными условиями используются так называемые зависимые начальные условия, а именно: значения токов, напряжений и их производных в начальный момент времени (t = 0).
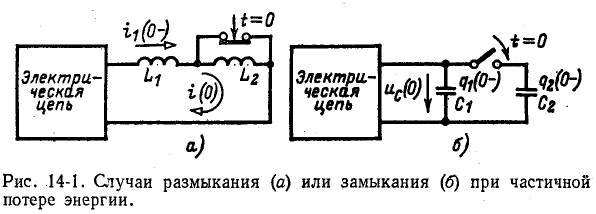
До сих пор нами исключались из рассмотрения случаи коммутации, при которых неизбежно между контактами возникает искра или дуга. Один из таких случаев показан на рис. 14-1, а. До коммутации ток проходит через индуктивность 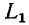
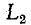
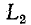
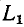
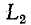
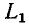
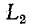
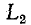
замкнуться и через межвитковую емкость. После быстрого погасания дуги токи в 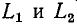
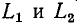
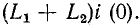
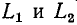
Найденный таким образом ток 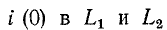
При коммутациях в цепях с емкостями при отсутствии сопротивлений также возможны весьма быстрые перераспределения зарядов, условно рассматриваемые как мгновенные. В этом случае применим принцип непрерывности суммарного заряда. Полученные при этом значения зарядов и напряжений на отдельных емкостях используются в расчете последующего переходного процесса как независимые начальные условия.
Например, в случае схемы на рис. 14-1, б принцип непрерывности суммарного заряда до и после коммутации выражается равенством
При сделанном допущении в остальной электрической цепи, соединенной с емкостями, не возникает бесконечно большого тока, так как суммарный заряд не изменяется скачкообразно при t=0.
В процессе рассматриваемой коммутации энергия электрического поля уменьшится, так как часть ее превратится в тепло в очень малом сопротивлении проводника при очень большом токе, а также сможет выделиться в искре и излучиться.
Установившийся и свободный режимы
В общем случае анализ переходного процесса в линейной цепи с сосредоточенными параметрами r, L, С и М сводится к решению обыкновенных линейных неоднородных дифференциальных уравнений, выражаюших законы Кирхгофа. Эти уравнения представляют собой линейную комбинацию напряжений, токов, их первых производных и интегралов по времени.
Например, если какая-нибудь э. д. с. е (t) включается в цепь, состоящую из последовательно соединенных r, L и С, то интегродифференциальное уравнение имеет вид:
Это уравнение после дифференцирования приводится к неоднородному дифференциальному уравнению второго
Как известно, общий интеграл такого^ уравнения равен сумме частного решения неоднородного уравнения и общего решения однородного уравнения.
Частное решение выражает установившийся режим, задаваемый источником.
Расчеты установившихся токов рассмотрены в предыдущих главах.
Общее решение физически определяет поведение цепи при отсутствии внешних источников электрической энергии и заданных начальных условиях. Функции, определяемые общим решением, называются свободными составляющими (токов, напряжений и пр.).
В случае, рассмотренном выше, однородное уравнение имеет вид:
и соответствующее ему характеристическое уравнение
Если корни характеристического уравнения обозначить через 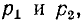
где 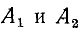
Полный переходный ток в цепи равен сумме установившегося и свободного токов:
Аналогично напряжение, заряд, магнитный поток и другие функции на любом участке цепи в переходном режиме состоят из установившейся и свободной составляющих.
На основании законов коммутации можно найти начальные независимые условия 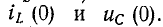
откуда
Итак, начальные значения свободных функций 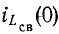
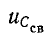
В частном случае при нулевых начальных условиях:
В зависимости от порядка дифференциальных уравнений, описывающих исследуемые переходные процессы, различают цепи первого, второго и более высокого порядков.
В цепях первого порядка накопление энергии происходит только в одном элементе, L или С в форме магнитной энергии, или электрической энергии . Одноконтурная цепь, содержащая элементы, в которых накапливается энергия обоих видов — магнитная « электрическая, представляет собой цепь второго порядка . Разветвленные цепи могут быть более высокого порядка.
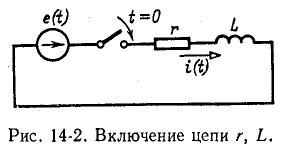
Переходный процесс в цепи r, L
Положим, что в момент t = 0 цепь, состоящая из сопротивления r и индуктивности L, включенных последовательно, присоединяется к источнику э. д. с. е (t) (рис. 14-2).
Дифференциальное уравнение для времени 
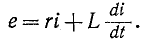
Характеристическое уравнение имеет вид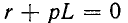
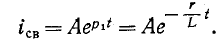
Переходный ток в цепи определится суммой установившегося и свободного токов:
Установившийся ток может быть найден, если задана э. д. с. е (t).
1) включение в цепь г, L постоянной э. д. с. £;
2) короткое замыкание цепи г, L
3) включение в цепь г, L синусоидальной э. д. с.
1. Включение в цепь г, L постоянной э. д. с.
При включении в цепь г, L постоянной э. д. с. Е установившийся ток равен Е’/г. Поэтому согласно (14-9)
Постоянная интегрирования А находится по начальному условию
Согласно уравнению (14-10) при t — 0
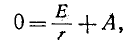
откуда 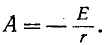
здесь 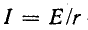
В начальный момент t = 0 э. д. с. самоиндукции 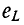
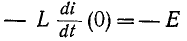
С течением времени э. д. с. самоиндукции убывает, а ток в цепи возрастает, асимптотически приближаясь к установившемуся значению.
На рис. 14-3 показаны кривые установившегося, свободного и переходного токов; на том же рисунке изображена кривая напряжения на индуктивности 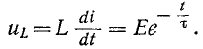
Из курса математического анализа известно, что если
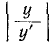
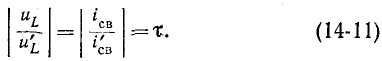
Величина 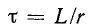
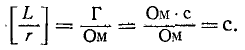
Выражение (14-11) показывает, что постоянная времени графически определяется длиной подкасательной к кривой 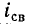
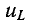
Нарастание тока происходит тем быстрее, чем меньше постоянная времени и соответственно чем быстрее убывает э. д. с. самоиндукции. Для различных моментов времени ток в цепи, выраженный в процентах конечного (установившегося) значения составляет:
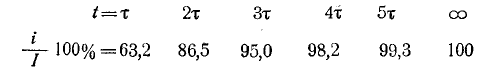
Следовательно, постоянная времени цепи г, L равна промежутку времени, в течение которого свободная составляющая тока убывает в е = 2,718 раза и соответственно ток в этой цепи, включенной на постоянное напряжение, достигает 63,2% своего установившегося значения.
Как видно из рис. 14-3 и приведенной выше таблицы», переходный процесс теоретически длится бесконечно долго. Практически же можно считать, что он заканчивается спустя
2. Короткое замыкание цепи r, L.
Положим, что цепь r, L, присоединенная к источнику постоянного или переменного напряжения, замыкается при t = 0 накоротко (рис. 14-4, а). В образовавшемся при этом контуре r, L благодаря наличию магнитного поля индуктивной катушки ток исчезает не мгновенно: э. д. с. самоиндукции, обусловленная убыванием магнитного потока, стремится поддержать ток в контуре за счет энергии исчезающего магнитного поля.
По мере того как энергия магнитного поля постепенно рассеивается, превращаясь в сопротивлении г в тепло, ток в контуре приближается к нулю.
Процесс, происходящий в короткозамкнутом контуре г, L, является свободным; установившийся ток в данном случае равен нулю.
Положив в (14-9) 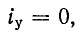
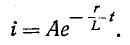
Постоянная интегрирования А находится из начального условия
здесь i (0—) — значение тока в индуктивности в момент, непосредственно предшествовавший короткому замыканию; оно может быть положительным или отрицательным.
На рис. 14-4, б изображены кривые спада тока в короткозамкнутом контуре и кривая напряжения на индуктивности

Постоянная времени контура 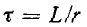
Переходный процесс в короткозамкнутом контуре заканчивается теоретически при 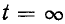
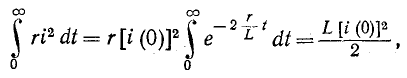
т. е. вся энергия, запасенная в магнитном поле катушки до коммутации.
Так же как и в предыдущем случае, переходный процесс в короткозамкнутом контуре можно практически считать законченным спустя
3. Включение в цепь r, L синусоидальной э. д. с.
При включении в цепь r, L синусоидальной э. д. с. 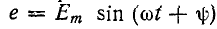
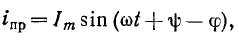
где 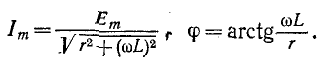
На основании (14-9) 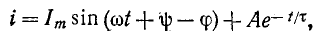
где 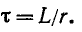
Постоянная интегрирования определяется по начальному условию
Следовательно, 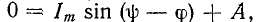
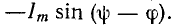
На рис. 14-5, а изображены кривые 
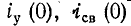
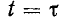
контура Q и обратно пропорциональна частоте 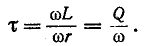
Если в момент коммутации (t = 0) ток 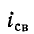
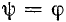
Если же коммутация происходит при 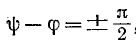
а именно 
гает экстремального значения (положительного или отрицательного) в конце первого полупёриода. Однако даже в предельном случае, когда r= 0 и, следовательно, 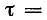
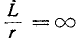
При достаточно большой постоянной времени 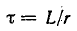
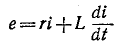
можно пренебречь по сравнению со вторым слагаемым, приняв приближенно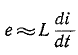
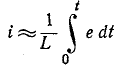
Следовательно, цепь с последовательно соединенными сопротивлением и индуктивностью при большой постоянной времени можно рассматривать как интегрирующее звено.
В свою очередь при достаточно малой постоянной времени, пренебрегая вторым слагаемым уравнения, приближенно получаем:
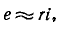
откуда
.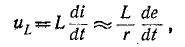
т. e. цепь с последовательно соединенными сопротивлением и индуктивностью при малой постоянной времени представляет собой дифференцирующее звено.
В обоих случаях функция е(t) может быть произвольной.
Интегрирующие и дифференцирующие звенья входят в качестве элементов в системы автоматического управления и регулирования.
Переходный процесс в цепи r, С
Положим, что в момент t = О цепь, состоящая из сопротивления г и емкости С, включенных последовательно, присоединяется к источнику э. д. с. е (t) (рис. 14-6).
На основании второго закона Кирхгофа уравнение для времени t 
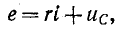
где 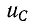
С учетом того, что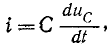
получим:
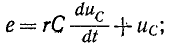
здесь искомой величиной является напряжение на емкости.
Характеристическое уравнение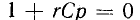
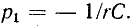
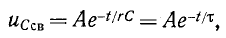
Переходное напряжение на емкости равно сумме принужденного и свободного напряжений:
В свою очередь ток в контуре
1) включение в цепь г, С постоянной э. д. с.
2) короткое замыкание цепи r, С
3) включение в цепь r, С синусоидальной э. д. с.
Включение в цепь r, С постоянной э. д. с.
Включим постоянную э. д. с. Е в цепь с сопротивлением г и предварительно заряженной емкостью С (полярности заряженной емкости указаны на рис. 14-6 знаками + и —); начальное напряжение на емкости
(0) обозначим для простоты через U.
Установившееся напряжение на емкости равно э. д. с. источника. Поэтому согласно (14-12)
Постоянная интегрирования А, входящая в (14-14), находится по начальному условию:
При t = 0 имеем 
Согласно (14-13) ток в контуре
Если Е > U, то с течением времени напряжение на емкости возрастает, стремясь к установившемуся значению Е, а ток убывает, стремясь в пределе к нулю; на рис. 14-7, а изображены кривые нарастания 
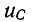
Если Е 0), убывающей (с 0) или убывающей (с 1 В случае, когда э. д. с. изменяется в виде импульса, имеющего кусочно-аналитическую форму, представляется часто целесообразным применять интеграл Дюамеля
токи же 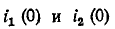
Подстановка в эти уравнения найденных значений 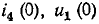
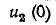
Начальное значение производной тока в индуктивности определяется также из уравнения Кирхгофа:
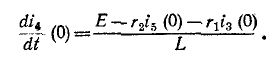
Пример (4-2. Определить ток i в иепи на рис. 14-17, если известно, что е = E = 100 В,
Подстановка заданных значений в приведенное выше характеристическое уравнение дает:
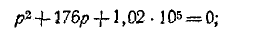
корни характеристического уравнения комплексные:
В начальный момент 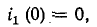
Производная тока по времени
В начальный момент
Следовательно, в начальный момент напряжение на ветви 
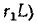
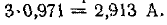
производной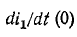
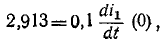
Следовательно, подставляя значение 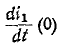
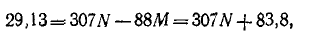
откуда
Итак, 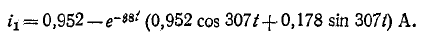
Переходные процессы в цепях с распределенными параметрами
Переходные процессы в цепях с распределенными параметрами (в линиях, обмотках электрических машин и т. п.) возникают при коммутациях, передаче непериодических сигналов или под влиянием внешнего электромагнитного поля (например, при грозовых разрядах). Для исследования переходных процессов в однородных цепях с распределенными параметрами пользуются дифференциальными уравнениями (11-2) в частных производных: 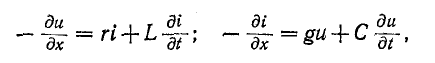
где r, L, g и С — параметры цепи на единицу длины; х — координата рассматриваемой точки, отсчитываемая от начала цепи.
В общем виде решение этих дифференциальных уравнений достаточно сложно. Решение упрощается, если пренебречь потерями В этом случае
е. считать, что r и g равны нулю.
и используя (14-29), получаем: 
Дифференциальное уравнение (14-30) известно в математической физике под названием уравнения ко—лебаний струны. Его решение дано Даламбером и имеет вид: 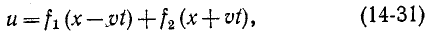
где 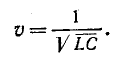
Первая слагающая представляет собой одиночную прямую волну напряжения, которая без изменения перемещается в сторону возрастающих х, т. е. от начала к концу цепи. Для всех значений х, при которых 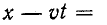
Вторая слагающая представляет собой одиночную о б -ратную волну напряжения, которая без изменения перемещается в противоположном направлении.
Для нахождения тока произведем замену переменных, обозначив 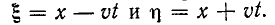
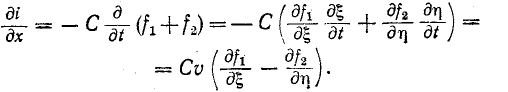
Но
Интегрирование последнего уравнения дает 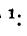
Выражения (14-31) и (14-32) записываются сокращенно:
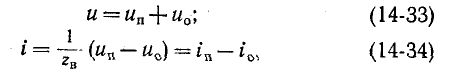
здесь 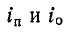
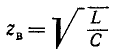
Следовательно, напряжение и ток прямой и соответственно обратной волн связаны законом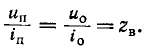
Аналогичный результат был получен для установившихся прямой и обратной волн при рассмотрении синусоидального режима в однородной линии. Физически установившиеся волны представляют собой бесконечные суммы прямых и обратных одиночных волн, отраженных от обоих концов линии.
Итак, при отсутствии потерь в однородной цепи с распределенными параметрами напряжение и ток могут быть представлены как сумма и разность двух волн, движущихся с одинаковой скоростью 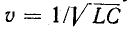
Если на пути распространения волны встречается неоднородность, например воздушная линия переходит в кабельную или волна достигает конца линии (разомкнутого или замкнутого через сопротивление или на короткое), происходит отражение волны. В зависимости от характера неоднородности отражение может быть частичным или полным. В первом случае наряду с отраженной волной возникает преломленная волна, распространяющаяся за место нарушения однородности; во втором случае преломленная волна отсутствует.
Обозначим 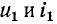
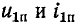
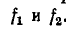
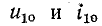
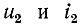
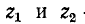
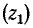
В месте неоднородности выполняется условие равенства
напряжений и токов: 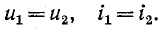
Следовательно, 
Подстановка в (14-36) значений 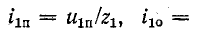
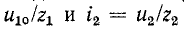
В результате совместного решения уравнений (14-35) — (14-37) находятся отраженная 
где 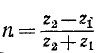
Соответственно ток отраженной волны
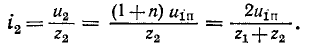
Последнее выражение показывает, что ток в конце линии после отражения можно найти как ток в эквивалентной цепи, в которую включается напряжение, равное двойному напряжению падающей волны, и которая состоит из волнового сопротивления первой линии 
Опишем процесс включения однородной линии без потерь. После присоединения линии к источнику э. д. с. по линии начнет распространяться зарядная волна, создающая напряжение и ток. Если в конце линии присоединена нагрузка, равная волновому сопротивлению линии,
то падающая волна, достигнув ее, не отразится и в линии сразу наступит установившийся режим. Если же нагрузка с линией не согласована, то падающая зарядная волна, достигнув конца линии, претерпит отражение. Распространяясь в обратную сторону, отраженная волна сложится с падающей, причем напряжения волн суммируются, а токи вычитаются (алгебраически). Достигнув начала линии, обратная волна снова отразится от источника э. д. с., как от короткозамкнутого конца; появится новая прямая волна напряжения и тока, которая также отразится от конца, и т. д. Процесс будет продолжаться до наступления установившегося режима. Теоретически в идеальной линии без потерь при чисто реактивной нагрузке процесс колебаний будет продолжаться бесконечно долго. В реальной линии при наличии потерь волны напряжения и тока будут постепенно затухать в направлении распространения.
Напряжение и ток в линии в произвольный момент времени определятся как алгебраические суммы и соответственно разности напряжений и токов прямых и обратных волн.
Пользуясь формулами и схемой замещения, описанной выше, можно найти напряжение и ток, возникающие в месте присоединения сосредоточенной нагрузки или перехода одной линии в другую (см. пример 14-3).
Следует отметить что индуктивность, включенная последовательно в линию, или емкость, включенная параллельно проводам линии, сглаживает фронт преломленных волн; активное сопротивление, включенное в линию параллельно, уменьшает преломленную волну.
Пример 14-3. К концу линии, имеющей волновое сопротивление 
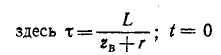
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Переходные процессы в линейных цепях
- Переходные процессы в нелинейных цепях
- Переходные процессы в электрических цепях с сосредоточенными параметрами
- Переходные процессы в колебательных контурах
- Цепи с взаимной индукцией
- Трехфазные цепи
- Периодические несинусоидальные напряжения и токи в линейных цепях
- Нелинейные цепи переменного тока
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Источник
Как решать задачи о прохождении тока через электрические схемы
В предыдущих статьях мы разобрали популярные учебные задачи по теории вероятностей: задачи про подбрасывания игральных кубиков и монеток, задачи про стрелков и станки.
В этой статье мы рассмотрим задачи вида
«задана схема электрической цепи с надежностью элементов (или вероятностями выхода из строя), найти вероятность работы цепи (или вероятность разрыва цепи)».
Задачи могут иметь чуть разные формулировки, но принцип решения для них одинаков, и его мы изучим, чтобы суметь решать такие задачи со схемами любой сложности.
Далее:
- Базовые события, обозначения и формулы
- Последовательно или параллельно?
- Усложняем схему цепи
- Примеры решений
- На закуску: схема с мостиком
- Полезные ссылки
- Решебник
Понравилось? Добавьте в закладки
Базовые события, обозначения и формулы
Самое первое, с чего мы начнем — формализация задачи (и решение любой своей задачи рекомендую начинать с этого). А именно, мы введем основные события:
$X$ = (Цепь работает) = (Цепь пропускает ток) и противоположное ему:
$overline{X}$ =(Цепь не пропускает ток) = (Произошел разрыв в цепи).
$A_i$ = (Элемент i работает, пропускает ток) и $overline{A_i}$ =(Элемент i отказал, не пропускает ток), $i=1,2,…,n$.
Обычно в условии задачи известны вероятности работы элементов (надежности): $p(A_i)=p_i$ или вероятности отказа $p(overline{A_i})=q_i=1-p_i$, $i=1,2,…,n$.
Также напомним основные формулы (из темы действий с событиями, формулы сложения и умножения вероятностей), которые пригодятся в решении этого типа задач.
Для независимых в совокупности событий (а отказы/работа элементов цепи — именно такие):
$$
P(A cdot B) = P(A) cdot P(B); quad(1)
$$
$$
P(A+B) = P(A)+P(B)-P(A)cdot P(B); quad(2)
$$
$$
P(A_1+A_2+…+A_n)=1-P(overline{A_1})cdot P(overline{A_2})cdot … cdot P(overline{A_n}). quad(3)
$$
Последовательно или параллельно?
Еще немного времени посвятим теории, вспомним о том, как могут соединяться элементы в цепи.
Последовательное соединение
Элементы цепи «нанизаны» на провод один за другим (следуют один за другим, отсюда и «последовательно»). Если откажет один любой — ток в цепи прервётся. Или, иначе говоря, цепь работает тогда и только тогда, когда ВСЕ элементы работают. В терминах теории вероятностей получаем произведение событий: $X=A_1 cdot A_2 cdot A_3$, а вероятность работы цепи равна
$$
P(X)=P(A_1 cdot A_2 cdot A_3)= P(A_1) cdot P(A_2) cdot P(A_3) =p_1 cdot p_2 cdot p_3.
$$
Если в цепи последовательно соединены не три, а больше независимо работающих элементов, формула легко обобщается и получаем:
$$
P(X) = p_1 cdot p_2 cdot …cdot p_n; qquad P(overline{X})=1-p_1 cdot p_2 cdot …cdot p_n. quad(4)
$$
Параллельное соединение
Тут тоже сама схема дает нам подсказку, когда мы видим, что элементы в схеме расположены как бы на параллельных проводах, речь идет о параллельном соединении.
В этом случае если откажет, скажем, элемент 1, ток может пройти через 2. Если откажут 1 и 2, ток пройдет через 3. И только если ВСЕ элементы откажут, цепь разорвется.
Еще говорят, цепь работает, если работает хотя бы один элемент в ней, в терминах теории вероятностей — это сумма событий: $X=A_1+A_2+A_3$.
Используем формулу (3) чтобы записать вероятность работы такой цепи:
$$
P(A_1+A_2+A_3)=1-P(overline{A_1})cdot P(overline{A_2}) cdot P(overline{A_3})=1-q_1 cdot q_2 cdot q_3.
$$
И обобщим на случай $n$ параллельных элементов в цепи:
$$
P(X) = 1-q_1 cdot q_2 cdot …cdot q_n; qquad P(overline{X})=q_1 cdot q_2 cdot …cdot q_n. quad(5)
$$
Важно запомнить правило
Последовательному соединению соответствует произведение событий,
параллельному соединению — сумма событий.
Усложняем схему цепи
И все это была присказка к настоящему решению задач. Конечно, даже если у вас простая контрольная, схема с «тремя лампочками подряд» вряд ли попадется. Давайте посмотрим на типовые электрические схемы, для которых надо находить надежность в задачах:
Как для таких схем выписывать вероятности? Нам нужно научиться делать декомпозицию: выделять уровни схемы и определять тип соединения на каждом уровне.
Возьмем для примера левую верхнюю схему:
Работаем с первым уровнем схемы. Нужно мысленно выделить крупные части, которые между собой соединены одинаково (параллельно или последовательно). В данном случае видно три группы элементов, соединенных последовательно. Выделим для наглядности цветом:
То есть тип схемы на первом уровне — последовательный:
Как мы уже знаем, если соединение последовательное, нужно перемножать события, то есть
$$
X=X_1 cdot X_2 cdot X_3,
$$
$X_1$ — работает первая группа элементов,
$X_2$ — работает вторая группа элементов,
$X_3$ — работает третья группа элементов.
Теперь смотрим на каждую группу. В первой группе всего один элемент, то есть она работает, когда работает первый элемент цепи ($X_1=A_1$). Мы дошли до элемента, разбор этой группы закончен.
А вот дальше интереснее. Рассмотрим поближе вторую группу:
В ней сразу выделим цветом подгруппы элементов. Видно, что вторая группа имеет уже параллельную структуру из розовых и фиолетовых элементов (они «висят» на параллельных линиях, это второй уровень вложенности схемы). А вот внутри розовые соединены последовательно (розовая группа работает — $A_4 cdot A_5$), фиолетовые элементы также между собой последовательно (фиолетовая группа работает — $A_2 cdot A_3$). Это уже третий уровень вложенности и он заканчивается отдельными элементами, значит, разбор окончен.
Так как розовая и фиолетовая группа соединены параллельно, речь идет о сумме этих событий, то есть вторая группа работает если:
$$X_2 = A_2 cdot A_3 + A_4 cdot A_5.$$
Абсолютно аналогично разбирается третья подгруппа (она совпадает по структуре со второй):
$$X_3 = A_6 cdot A_7 + A_8 cdot A_9.$$
Сводим все в одну формулу и выпишем искомое событие (Цепь работает исправно):
$$
X=X_1 cdot X_2 cdot X_3 = A_1 cdot left( A_2 cdot A_3 + A_4 cdot A_5 right) cdot left( A_6 cdot A_7 + A_8 cdot A_9right).
$$
Теперь переходим ко второму этапу решения задачи. Не забываем, что мы решаем задачу по теории вероятностей и надо определить вероятность того, что ток проходит в цепи. Будем использовать формулы (1)-(3).
Так как вероятность произведения для независимых событий равна произведению вероятностей, получим:
$$
P(X)= P left( A_1 cdot left( A_2 cdot A_3 + A_4 cdot A_5 right) cdot left( A_6 cdot A_7 + A_8 cdot A_9right) right) =\
= P (A_1) cdot P left ( A_2 cdot A_3 + A_4 cdot A_5 right ) cdot P left( A_6 cdot A_7 + A_8 cdot A_9right) =
$$
Для множителей с суммой событий внутри используем формулу (2):
$$
= P (A_1) cdot left[ P(A_2 cdot A_3) + P(A_4 cdot A_5) — P(A_2 cdot A_3 cdot A_4 cdot A_5) right] cdot left[ P(A_6 cdot A_7) + P(A_8 cdot A_9) — P(A_6 cdot A_7 cdot A_8 cdot A_9)right] =
$$
И снова раскрываем вероятности произведений:
$$
= P (A_1) cdot left[ P(A_2) cdot P(A_3) + P(A_4) cdot P(A_5) — P(A_2) cdot P(A_3) cdot P(A_4) cdot P(A_5) right] cdot left[ P(A_6) cdot P(A_7) + P(A_8) cdot P(A_9) — P(A_6) cdot P(A_7) cdot P(A_8) cdot P(A_9)right].
$$
Перейдем к более компактной записи, положив $p_i=P(A_i)$:
$$
P(X)= p_1 cdot left[ p_2 cdot p_3 + p_4 cdot p_5 — p_2 cdot p_3 cdot p_4 cdot p_5 right] cdot left[ p_6 cdot p_7 + p_8 cdot p_9 — p_6 cdot p_7 cdot p_8 cdot p_9right].
$$
Если заданы надежности отдельных элементов $p_i$, подставляя их в формулу, можно найти вероятность работы схемы.
Алгоритм разбора схемы
- Выделяем в схеме основу: группы элементов, соединенные ТОЛЬКО последовательно или ТОЛЬКО параллельно между собой. Это верхний уровень. Записываем событие $X$ = (Цепь работает) как произведение или сумму соответственно.
- Каждую полученную группу анализируем также: ищем в ней подгруппы, соединенные только последовательно или только параллельно. Записываем событие соответственно типу соединения.
- Продолжаем до тех пор, пока не опустимся на уровень элементов (событий $A_i$).
- Подставляем все выражения в исходную формулу, получаем итоговую запись события $X$.
- Пользуясь формулами (1)-(3) выписываем вероятность события $P=P(X)$.
- Подставляем числовые значения $p_i, q_i$ и находим численное значение надежности схемы $P$.
- Если необходимо, находим вероятность отказа цепи $1-P$.
Примеры решений
Отработаем несколько раз этот алгоритм на примерах, чтобы он закрепился.
Пример 1. Дана схема включения элементов. Вероятность безотказной работы каждого элемента в течение времени Т равна р. Элементы работают независимо и включены в цепь по приведенной схеме. Пусть событие $А_i$ означает безотказную работу за время Т элемента с номером $i$ ($i=1,2,3,…$), а событие $В$ – безотказную работу цепи. Требуется:
1) Написать формулу, выражающую событие $В$ через все события $А_i$.
2) Найти вероятность события $B$.
3) Вычислить $Р(В)$ при $р=0,6$.
Приступим к разбору схемы. Можно увидеть, что на первом уровне мы имеем три группы, соединенные последовательно: (1), (2,3) и (4,5,6) элементы. Выделим их цветом для наглядности:
Значит, исходное событие можно представить в виде произведения трех событий $B=B_1 cdot B_2 cdot B_3$, где $B_i$ — работает $i$-aя группа элементов.
Первая группа элементов состоит из одного элемента, то есть $B_1=A_1$.
Вторая группа элементов состоит из двух элементов, соединенных параллельно (см. розовые), поэтому $B_2=A_2+A_3$.
Третья группа элементов (см. зеленые) состоит из трех элементов, ее можно представить как параллельное соединение двух подгрупп: (4 и 5, соединены последовательно) и (6), поэтому $B_3=A_4 cdot A_5 + A_6$.
Подставляем все и получаем выражение для события $B$
$$
B=B_1 cdot B_2 cdot B_3 = A_1 cdot (A_2+A_3) cdot (A_4 cdot A_5 + A_6).
$$
Теперь выразим вероятность безотказной работы цепи за время T. Сначала применим формулу (1), чтобы раскрыть произведение:
$$
P(B)=P left( A_1 cdot (A_2+A_3) cdot (A_4 cdot A_5 + A_6) right) = P(A_1) cdot P left( A_2+A_3 right) cdot P left( A_4 cdot A_5 + A_6 right) =
$$
Раскроем вторую вероятность по формуле (3), а третью по формуле (2), получим:
$$= P(A_1) cdot left(1 — P(overline{A_2}) cdot P(overline{A_3}) right) cdot left( P(A_4) cdot P(A_5) + P(A_6) — P(A_4) cdot P(A_5) cdot P(A_6) right).$$
Подставляем $P(A_i)=p$ и получим:
$$
p(B)=pcdot(1-(1-p)cdot(1-p))cdot(pcdot p + p -p cdot p cdot p) = pcdotleft(1-(1-p)^2right)cdot left(p+p^2-p^3right).
$$
Осталось только найти значение при $p=0,6$:
$$
p(B)= 0,6cdotleft(1-(1-0,6)^2right)cdot left(0,6+0,6^2-0,6^3right) approx 0,375.
$$
Пример 2. Найти вероятность обрыва цепи, если вероятность отказа каждого элемента равна 0,2, а отказы элементов – независимые события.
Пронумеруем элементы и сразу раскрасим схему, чтобы выделить ее структуру.
Это опять последовательная схема, но розовая группа состоит из двух элементов, соединенных параллельно, поэтому можем сразу выписать:
$$
X= A_1 cdot (A_2+A_3) cdot A_4 cdot A_5.
$$
Найдем вероятность этого события (работы цепи):
$$
P(X)= P left( A_1 cdot (A_2+A_3) cdot A_4 cdot A_5 right)= P(A_1) cdot P(A_2+A_3) cdot P(A_4) cdot P(A_5)= \
= P(A_1) cdot left( 1- P(overline{A_2}) cdot P(overline{A_3}) right) cdot P(A_4) cdot P(A_5).
$$
Вероятности отказа элементов цепи равна 0,2, вероятность работы элементов — 0,8, поэтому
$$
P(X)= 0,8 cdot left( 1- 0,2 cdot 0,2 right) cdot 0,8 cdot 0,8 = 0,492.
$$
Но в задаче требовалось найти вероятность обрыва цепи, это противоположное событие:
$$
P(overline{X}) = 1- P(X) = 1-0,492 = 0,508.
$$
Пример 3. Найти вероятность безотказной работы функциональной цепи, состоящей из независимо работающих элементов, если вероятность надежной работы элементов равна $p_1=p_2=p_3=p_4=0,8$, $p_5=p_6=p_7=0,9$.
Приступим к решению, сразу раскрасив схему. В этот раз схема на первом уровне имеет параллельное соединение: верхняя розово-зеленая группа и нижняя желтая находятся на параллельных линиях. Поэтому $X=X_1+X_2$, где $X_1$ — работает розово-зеленая линия, $X_2$ — работает желтая.
Для желтой группы, состоящей из трех последовательно расположенных элементов, сразу выписываем $X_2=A_5 cdot A_6 cdot A_7$.
Теперь рассмотрим верхнюю группу. Она состоит из двух подгрупп, связанных последовательно: розовой и зеленой. При этом каждая из них состоит из двух параллельно соединенных элементов. Записываем: розовая группа работает = $A_1+A_2$, зеленая группа работает = $A_3+A_4$, значит ток проходит через розово-зеленую группу $X_1 =(A_1+A_2) cdot (A_3+A_4)$.
Объединяем рассуждения и выписываем событие, соответствующее безотказной работе цепи:
$$
X=X_1+X_2 = (A_1+A_2) cdot (A_3+A_4) + A_5 cdot A_6 cdot A_7.
$$
Следующий шаг: выразить вероятность этого события. Во всех предыдущих примерах схема на первом уровне была последовательной, и событие выражалось как произведение. В этом случае схема на первом уровне параллельна, событие выглядит как сумма других событий, что немного усложняет выкладки. Для суммы событий можно использовать формулу (2) или (3), выбирая наиболее удобную в каждом конкретном случае.
В данном случае слагаемых всего два, поэтому возьмем формулу (2):
$$
P(X)= P left( (A_1+A_2) cdot (A_3+A_4) + A_5 cdot A_6 cdot A_7 right) = \
= P left( (A_1+A_2) cdot (A_3+A_4) right) + P left( A_5 cdot A_6 cdot A_7 right) — P left( (A_1+A_2) cdot (A_3+A_4) cdot A_5 cdot A_6 cdot A_7 right)
$$
Раскрываем все произведения по формуле (1):
$$
= P (A_1+A_2) cdot P(A_3+A_4) + P(A_5) cdot P(A_6) cdot P(A_7) — P (A_1+A_2) cdot P(A_3+A_4) cdot P(A_5) cdot P(A_6) cdot P(A_7) =
$$
По формуле (3) расписываем $P(A_1+A_2)=1-P(overline{A_1}) cdot P(overline{A_2}) = 1-q_1cdot q_2$ и $P(A_3+A_4)=1-P(overline{A_3}) cdot P(overline{A_4})= 1-q_3cdot q_4$.
Итого:
$$
P(X)= (1-q_1cdot q_2) cdot (1-q_3cdot q_4) + p_5 cdot p_6 cdot p_7 — \- (1-q_1cdot q_2) cdot (1-q_3cdot q_4) cdot p_5 cdot p_6 cdot p_7.
$$
Подставляем значения надежности элементов:
$$
P(X)= (1-0,2^2)^2 + 0,9^3 — (1-0,2^2)^2 cdot 0,9^3 approx 0,9788.
$$
Еще: другие уроки о решении задач по вероятности
На закуску: схема с мостиком
Для 99% учебных задач вам хватит той теории и примеров, что приведены выше: подробно изучите их и приступайте к своим примерам по аналогии. Но есть такие схемы, для которых нельзя выделить единую структуру на верхнем уровне — параллельную или последовательную, и весь алгоритм решения рушится.
Речь идет о схемах смешанного типа, еще их часто называют схемами с мостиком (мостиковые схемы). Типичная схема имеет такой вид:
Видно, что как ни крути, схему нельзя отнести ни к последовательным, ни к параллельным. Элемент №5 (мостик) «портит» тип схемы. Если его убрать (разорвать этот участок цепи), получим обычную параллельную структуру, а если предположить, что через этот участок всегда идет ток — последовательную (конкретные схемы изобразим ниже).
Поэтому для решения задачи о вычислении надежности подобной электросхемы используют формулу полной вероятности в форме теоремы разложения (см. подробнее тут, стр. 118)
Надежность цепи с избыточностью равна произведению вероятности безотказной работы $i$-го элемента цепи на вероятность безотказной работы оставшейся цепи (места подключения $i$-го элемента замкнуты накоротко) плюс произведение вероятности отказа того же $i$-го элемента на вероятность безотказной работы оставшейся цеии (места подключения $i$-го элемента разомкнуты).
То есть, для выделенного на схеме элемента-мостика рассматриваем две гипотезы:
$H_1$ = (Элемент 5 не пропускает ток), $P(H_1)=1- p_5 = q_5$;
$H_2$ = (Элемент 5 пропускает ток), $P(H_2)=p_5$.
Далее вычисляем надежность схемы при условии верности каждой из гипотез. Для наглядности нарисуем обе схемы:
Рассмотрим левую схему, верную при гипотезе $H_1$, через нее проходит ток, если $X|H_1 = A_1cdot A_3+ A_2cdot A_4$, вероятность
$$
P(X|H_1) = P(A_1cdot A_3+ A_2cdot A_4)= P(A_1cdot A_3)+ P(A_2cdot A_4) — P(A_1cdot A_3 cdot A_2cdot A_4)=\
=p_1 cdot p_3 + p_2 cdot p_4 — p_1 cdot p_2 cdot p_3 cdot p_4.
$$
Рассмотрим правую схему, верную при гипотезе $H_2$, и выпишем для нее аналогично событие и вероятность прохода тока:
$$
X|H_2 = (A_1+A_2)cdot (A_3+A_4),\
P(X|H_2) =P( (A_1+A_2)cdot (A_3+A_4)) = P(A_1+A_2)cdot P(A_3+A_4)=\ = (1-P(overline{A_1}) cdot P(overline{A_2})) cdot (1-P(overline{A_3}) cdot P(overline{A_4})) = (1-q_1cdot q_2) cdot (1-q_3cdot q_4).
$$
Тогда по формуле полной вероятности, надежность схемы равна:
$$
P(X)=P(X|H_1)cdot P(H_1) + P(X|H_2)cdot P(H_2) = \
= q_5 (p_1 cdot p_3 + p_2 cdot p_4 — p_1 cdot p_2 cdot p_3 cdot p_4) + p_5 (1-q_1cdot q_2) cdot (1-q_3cdot q_4).
$$
Аналогичным образом можно разбирать более сложные схемы (в которые более одного мостика), применяя на каждом этапе формулу полной вероятности (как бы вкладывая одну в другую).
Понравилось? Добавьте в закладки
Полезные ссылки по ТВ
|
|
Решебник по вероятности
А здесь вы найдете разные задачи по теории вероятностей с полными решениями (вводите часть текста для поиска своей задачи):




 Типичные неполадки в домашней электросети и их устранение
Типичные неполадки в домашней электросети и их устранение

 Какие кабели приобретать для прокладки домашней проводки?
Какие кабели приобретать для прокладки домашней проводки?



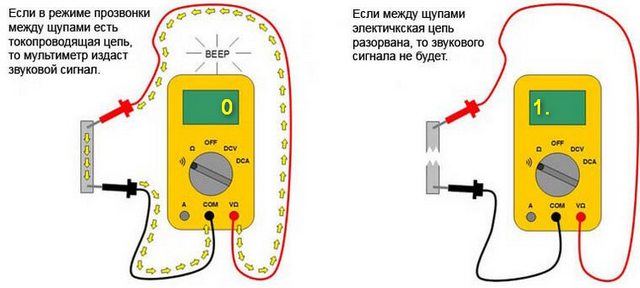


 Что важно знать о прокладке скрытой проводки в доме или квартире
Что важно знать о прокладке скрытой проводки в доме или квартире