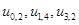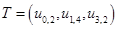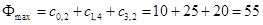Максимальный поток определяется с
помощью одного из основных понятий
теории сетей – разреза.
Разрез может быть представлен
как множество дуг, исключение которых
из сети сделало бы орграф несвязным.
Предположим, что дана некоторая сеть.
Разобьем множество вершин V
этой сети на два непересекающихся
подмножества
и
так, чтобы исток
попал в подмножество
,
а сток
– в подмножество
,
т.е.
.
В этом случае говорят, что на сети
произведен разрез, отделяющий исток
от стока
.
Пусть
— разрез на сети, представляющий
совокупность дуг, которые связывают
подмножества вершин A
и B. В разрез входят
дуги, обозначим их
,
начальные вершины которых принадлежат
подмножеству A, а
конечные – подмножеству B,
т.е.
.
А также в разрез входят дуги, обозначим
их
,
начальные вершины которых принадлежат
подмножеству B, а
конечные – подмножеству A,
т.е.
.
Пропускной способностью или
величиной разреза
называется величина
,
которая определяется следующей формулой:
.
(12.2.1)
Потоком через разрез
называется величина
,
которая определяется следующей формулой:
.
(12.2.2.)
Пример 12..
Рассмотрим сеть с заданными пропускными
способностями дуг, которые записаны в
круглых скобках.
Построим на сети некоторый поток,
величину которого по каждой дуге будем
записывать без скобок:
путь
:
,
значит, по этому пути пропускаем поток
в 2 единицы;
путь
:
,
значит, по этому пути пропускаем поток
в 3 единицы;
путь
:
,
значит, по этому пути пропускаем поток
в 1 единицу;
Проведем на этой сети, например, разрез
,
при котором вершины разбиты на подмножества
и
.
Тогда сам разрез состоит из дуг
,
,
,
,
т.е.
.
Так, например, пропускная способность
разреза
на рисунке равна
(ед.),
а поток через этот разрез составляет:
(ед.).
12.3. Алгоритм нахождения максимального потока на сети.
Если на сети сформирован некоторый
поток, то для ответа на вопрос: будет ли
он максимальным, используют теорему
Форда-Фалкерсона.
Теорема 12.1. (Теорема Форда-Фалкерсона)
Максимальный поток в сети равен
минимальной пропускной способности
разреза:
.
Доказательство теоремы – это алгоритм
определения максимального потока по
сети.
Алгоритм нахождения максимального потока на сети.
Этап 1. Насыщение потока.
Шаг 1. Сформировать произвольный
начальный поток.
Шаг 2. Найти оставшиеся возможные
пути из истока
в сток
,
имеющие только ненасыщенные дуги. Если
такой путь найден, то переходим к шагу
3. Если путь не найден, то переходим к
шагу 4.
Шаг 3. Увеличить поток по
найденному пути таким образом, чтобы
одна из дуг стала насыщенной.
Шаг 4. Получившийся поток насыщен.
Этап 2. Пометка вершин сети.
(Перераспределение потока.)
Шаг 5. Вершину
пометить
.
Шаг 6. Пусть
– любая из уже помеченных вершин;
– произвольная непомеченная вершина,
смежная с вершиной
.
Вершину
помечаем
,
если данные вершины соединены ненасыщенной
дугой
,
и помечаем
,
если соединены непустой дугой
.
После пометки вершин возможны два
случая: вершина
оказалась либо помеченной, либо
непомеченной.
Шаг 7. Вершина
оказалась помеченной. Значит, существует
последова-тельность помеченных вершин
от
к
.
В этой последовательности каждая
последующая вершина помечена буквой
предыдущей вершины. На дугах
последовательности определяем новый
поток. Увеличиваем на
единиц поток на дугах, имеющих направление
от
к
и уменьшаем на
единиц поток на дугах, имеющих обратное
направление. Число
равно наименьшей разнице между пропускной
способностью и потоком дуг, входящих в
последовательность. Заметим, что поток
можно увеличивать (уменьшать) на прямых
(обратных) дугах настолько, пока одна
из дуг не станет насыщенной (пустой).
Далее вновь переходим к пометке вершин
(шаг 5). Перераспределение потока сохраняет
все его свойства и увеличивает поток
на
единиц в вершину
.
Этап 3. Определение максимального
потока.
Шаг 8. Вершина
осталась непомеченной. Пусть
– множество всех помеченных вершин,
– множество всех непомеченных вершин.
Тогда дуги, связывающие два подмножества
вершин
и
,
определяют разрез
.
Таким образом, найден поток
и разрез
,
для которого выполняется условие
.
Пример 2.2.
На сети из примера 12.1. сформировать
максимальный по величине поток,
направленный из истока
в сток
.
Выписать ребра, образующие на сети
разрез минимальной пропускной способности.
Решение. Этап 1.
Шаг 1. Воспользуемся тем, что в
примере 12.1. был уже сформирован некоторый
поток на сети.
Шаг 2. Путь
содержит насыщенную дугу
.
Больше нельзя добавить потока по этому
пути. Пути
,
и
содержат насыщенные дуги.
Но путь
имеет две дуги, которые еще ненасыщенные.
Шаг 3. Увеличиваем поток по
найденному пути:
.
Значит, на этом пути поток увеличиваем
на 1 единицу, и тем самым дуга
стала насыщенной.
Шаг 4. Таким образом, получаем
насыщенный поток, поскольку каждый
рассмотренный путь содержит хотя бы
одну насыщенную дугу.
Этап 2.
Выясним, является ли построенный поток
максимальным по величине. Строим сеть,
на которой отметим все вершины и
ненасыщенные дуги. На этой сети разность
пропускных способностей дуги и проходящего
по ней потока обозначим числом в
квадратных скобках.
Шаг 5, 6. Вершину
пометить
.
На шаге 6 предусматривается пометка
вершин, смежных с вершиной I,
соединенных ненасыщенными дугами. Но
на построенной сети таких вершин нет.
В результате вершина S
оказалась непомеченной.
Этап 3. Шаг 8. Так как
вершина S непомеченная,
то поток, сформированный на сети,
получился максимальным.
Строим разрез на сети. Разбиваем множество
вершин на два подмножества: A
и B. Так как только
одна вершина оказалась помеченной, то
множество A состоит
из одной вершины I, а
остальные образуют множество B:
.
Проводим разрез
,
который состоит из дуг
и
:
.
Определяем величину максимального
потока
:
(ед.)
Пример 2.3.
На заданной сети в скобках указаны
пропускные способности дуг. Требуется
сформировать на сети максимальный
поток, направленный из истока
в сток
,
и выписать ребра, образующие на сети
разрез минимальной пропускной способности.
Решение. Этап 1.
Сформируем на сети какой-либо начальный
поток. Рассмотрим путь
.
Поскольку
,
по этому пути пропускаем поток в 2
единицы. На сети значение потока обозначим
числами без скобок. По пути
пропускаем поток в 4 единицы, так как
.
По пути
пропускаем поток в 3 единицы, так как
.
Таким образом, начальный поток имеет
вид:
,
,
.
Начальный поток изображен на рисунке.
(2)
k
p
2
(7)
(6)
(2)
2
2
(4)
(5)
I
S
(6)
4
c
d
4
4
(3)
3
(3)
(5)
(1)
(1)
(2)
3
a
3
b
(6)
Каждый из рассмотренных путей содержит
насыщенную дугу, поэтому эти пути
насыщенные. На сети есть еще пути, которые
содержат ненасыщенные дуги, а именно:
,
и
.
Для первого пути дополнительно увеличим
поток на 2 единицы, так как
.
Второй и третий пути содержат одну и ту
же дугу
с минимальной для них оставшейся
разностью
.
Поэтому для увеличения потока на 1
единицу выберем, например, путь
.
Т
каждый из этих путей содержит насыщенную
дугу, следовательно, полученный поток
– насыщенный.
Выясним, является ли построенный поток
максимальным. Изобразим сеть, на которой
отметим все вершины и ненасыщенные
дуги. На этой сети разность пропускной
способности дуги и проходящего по ней
потока обозначим числом в квадратных
скобках. Пропускную способность дуги,
по которой поток не проходит, оставим
в круглых скобках.
Видим, что на сети исток I
и сток S связаны дугами.
Значит, можно добавить какое-то количество
потока по ненасыщенным дугам, при этом
придется перераспределить поток.
Этап 2.
На построенной сети помечаем вершины.
Вершину
пометим
.
Смежную ей вершину
помечаем
,
так как эти вершины соединяет ненасыщенная
дуга
.
Вершину
помечаем
,
так как вершины
и
соединяет ненасыщенная дуга
.
Вершину
помечаем
,
так как вершины
и
соединяет непустая дуга
.
Вершины
и
помечаем
,
так как они соединены с вершиной
ненасыщенными дугами
и
.
Вершина
смежная вершине
,
и эти вершины соединены ненасыщенной
дугой
,
поэтому вершину
помечаем
.
Вершина
смежная вершине
,
и эти вершины соединены ненасыщенной
дугой
,
поэтому вершину
помечаем
.
Вершина
оказалась помеченной. Значит, существует
последовательность помеченных вершин
от
к
:
.
В этой последовательности каждая
последующая вершина помечена буквой
предыдущей вершины. Перераспределим
поток на этом пути. Определим число
:
.
Увеличиваем на 1 единицу поток на дугах,
имеющих направление от
к
:
,
,
,
.
Уменьшаем на 1 единицу поток на дугах,
имеющих обратное направление:
.
Получаем следующую сеть с новым
сформированным потоком, который изображен
на рисунке.
Проверим, будет ли построенный поток
максимальным. Изобразим сеть, на которой
отметим все вершины и ненасыщенные
дуги, как сделали выше.
Вновь помечаем вершины. Вершину
пометим
.
Смежную ей вершину
помечаем
,
так как эти вершины соединяет ненасыщенная
дуга
.
Все остальные вершины, в том числе и
вершина
,
остаются непомеченными. Значит, поток
на сети максимальный.
Этап 3.
Как видно на последней сети исток
и сток
не связны дугами. Значит, поток,
изображенный на предпоследней сети,
является максимальным.
Строим разрез на сети. Разбиваем множество
вершин на два подмножества: A
и B. Помеченные вершины
образуют множество
,
непомеченные – множество
.
Проводим разрез
,
который состоит из дуг
,
,
,
:
.
Определяем величину максимального
потока
:
(ед.)
Соседние файлы в папке дискретка
- #
- #
- #
- #
- #
- #
- #
- #
- #
| Определение: |
| -разрезом (англ. s-t cut) в сети называется пара множеств , удоволетворяющих условиям:
|
| Определение: |
| Пропускная способность разреза (англ. capacity of the cut) обозначается и вычисляется по формуле: . |
| Определение: |
| Поток в разрезе (англ. flow in the cut) обозначается и вычисляется по формуле: . |
| Определение: |
| Минимальным разрезом (англ. minimum cut) называется разрез с минимально возможной пропускной способностью |
| Лемма (о величине потока): |
|
Пусть — разрез в . Тогда . |
| Доказательство: |
|
| Лемма (закон слабой двойственности потока и разреза): |
|
Пусть — разрез в . Тогда . |
| Доказательство: |
| , из-за ограничений пропускных способностей . |
| Лемма (о максимальном потоке и минимальном разрезе): |
|
Если , то поток — максимален, а разрез — минимален. |
| Доказательство: |
|
Из закона слабой двойственности следует, что для любых двух разрезов и в сети , так как . Очевидно, что эта точка определяет максимальный поток среди всех потоков и минимальный разрез среди всех разрезов сети . |
Среди всех разрезов сети разрез с минимальной пропускной способностью определяет максимальный поток в сети.
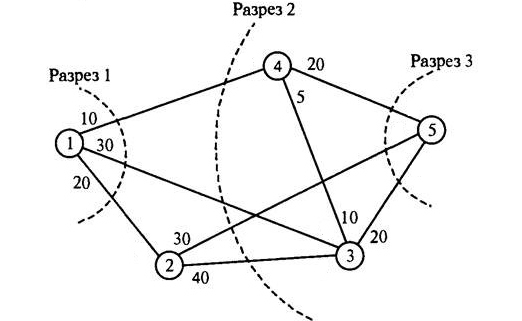
| Разрез | «Разрезанные» ребра | Пропускная способность |
| 1 | (1,2),(1,3),(1,4) | 10+30+20=60 |
| 2 | (1,3),(1,4),(2,3),(2,5) | 30+10+40+30=110 |
| 3 | (2,5),(3,5),(4,5) | 30+20+20=70 |
Источники информации
- Кормен, Томас Х., Лейзерсон, Чарльз И., Ривест, Рональд Л., Штайн Клиффорд Алгоритмы: построение и анализ, 2-е издание. Пер. с англ. — М.:Издательский дом «Вильямс», 2010. — 1296 с.: ил. — Парал. тит. англ. — ISBN 978-5-8459-0857-5 (рус.)
- Википедия: Разрез графа
- Википедия: Разрез графа (англ.)
Представим, что у нас есть диграф и две вершины — источник и сток. У каждого ребра есть вес, который называется его пропускной способностью. Нам нужно пропустить как можно больше материала через диграф от источника к стоку. Это называется потоком, а взвешенный диграф — сетью. Таким образом мы строим сетевой поток.
Например, источник — это
, а сток —
:

Первое число, выделенное красным на каждом ребре — это значение потока, а второе — пропускная способность. В этом случае поток не оптимальный, так как через сеть можно пропустить больше вещей, чем
единиц.
Количество потока на ребре не может превышать его пропускную способность. Еще общее количество потока в вершину должно быть равно общему количеству потока из этой вершины, за исключением источника и стока. В итоге поток проходит через вершины, которые не создают и не потребляют поток.
Общее объем потока, который проходит через сеть, называется величиной потока. Это количество можно найти, если посчитать:
-
Общий поток, который выходит из источника
-
Общий поток, который входит в сток
Многие реальные проблемы можно смоделировать с помощью сетей потоков. Например, источник — это место, где мы добываем сырье. Его нужно доставить на завод — сток. Края — это различные маршруты, по которым мы можем отправить сырье, а мощность — сколько материала можно доставить по этим маршрутам.
Если предположить, что транспортная сеть — это ограничивающий фактор, то нас интересует, сколько сырья мы можем доставить на фабрику.
Многие несвязанные проблемы теории графов можно преобразовать в проблемы сетевых потоков.
Как найти минимальный разрез в сети
Решить задачу нахождения максимального потока в транспортной сети с помощью алгоритма Форда—Фалкерсона, и построить разрез сети S.
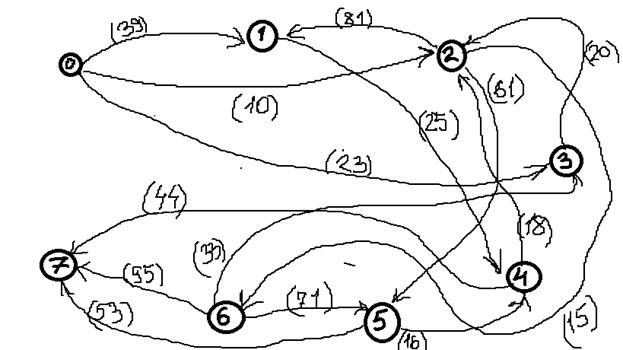
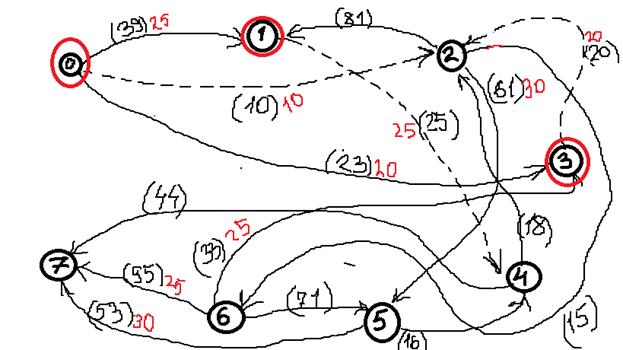
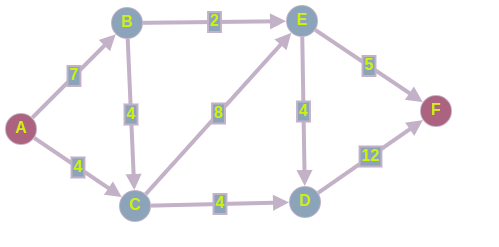
Исходные данные:
Дана сеть S(X,U) 
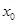
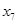
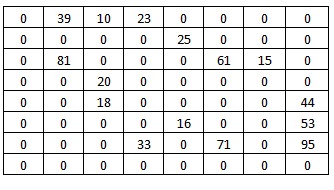
Значения пропускных способностей дуг 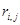
r[0,1] = 39; r[4,7] = 44; r[6,3] = 33; r[5,7] = 53; r[0,2] = 10;
r[4,2] = 18; r[6,7] = 95; r[5,4] = 16; r[0,3] = 23; r[2,5] = 61;
r[2,1] = 81; r[6,5] = 71; r[1,4] = 25; r[2,6] = 15; r[3,2] = 20
1. Зададим на сети нулевой поток (на всех дугах величина потока 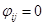
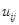
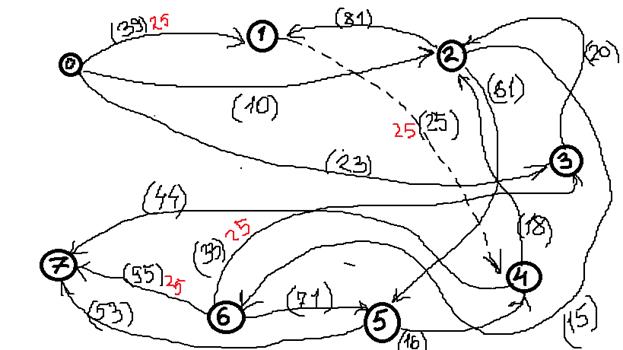
2. Выбираем на сети (произвольно) путь, ведущий из вершины x0 в вершину x7:
X0-X1-X4-X6-X7
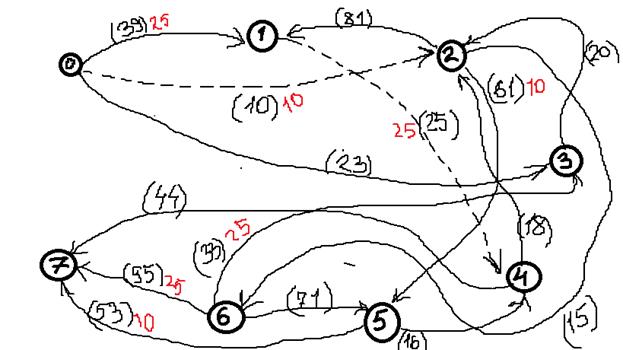
3. Находим 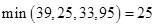
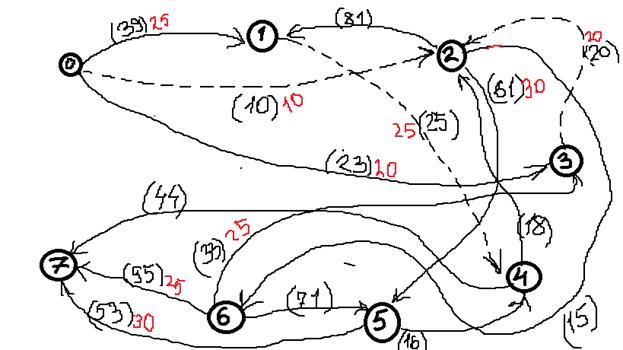
4. Выбираем еще один путь, например: Х0-Х2-Х5-Х7, находим 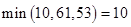
5. Выбираем еще один путь, например: Х0-Х3-Х2-Х5-Х7, находим 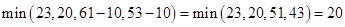
6. Более путей от Х0 до Х7 нет, суммируем увеличения потока: 25+10+20=55.
Вывод: максимальный поток равен 55.
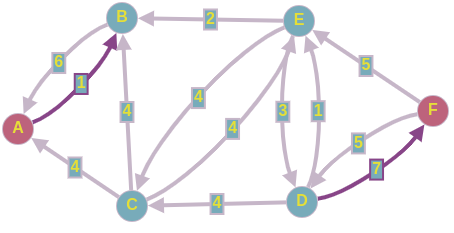
2) Построить разрез сети S.
Процедура «пометок вершин».
Начальное состояние: все вершины не имеют пометок.
Вершине Х0 приписывается пометка. Всем вершинам 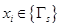
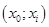
Определяем дуги минимального разреза: это дуги, начала которых находятся в помеченных вершинах, а концы — в непомеченных вершинах.
Это дуги:
Таким образом, минимальный разрез данной сети
Вычисление величины максимального потока
Алгоритм Форда-Фалкерсона
Привет, Хабр!
В свободное от учебы время пишу статьи, которых мне не хватало несколько лет назад.
При решении задачи о максимальном потоке я столкнулся с тем, что во всех мне известных источниках было дано формальное описание самих алгоритмов, что очень сильно затрудняло понимание изложенного материала. И в этой статье я попробую на базовом уровне разобрать Алгоритм Форда-Фалкерсона на конкретном примере, чтобы после прочтения данной статьи, вы хотя бы понимали основную суть самого алгоритма.
Постановка задачи
Имеется следующий ориентированный граф, в котором вес ребра обозначает пропускную способность между вершинами. Нужно найти максимальный поток, который можно пропустить из истокав сток.
Исходный граф
Как работает сам алгоритм?
Следует понимать остаточную сеть как тот же граф, который имеется на входе, но в этом случае мы будем производить над ним некоторые операции:
Отправлять определенное количество потока из текущей вершины в соседние.
Возвращать определенное количество потока из соседних вершин в текущую.
В начальный момент времени поток, который мы хотим провести через нашу сеть, должен быть равен нулю. Остаточная сеть совпадает с исходной сетью.
Находим любой путь из истока в сток в остаточной сети. Если путь не находим, утверждается, что поток является максимальным.
Пускаем через найденный путь поток равный минимальному весу ребра, которое входит в множество рёбер найденного пути.
Из веса рёбер на этом пути высчитываем размер потока, который мы пустили.
А к весу обратных рёбер (будем считать, что они существуют в остаточной сети и равны 0) прибавляем размер потока. Другими словами, на предыдущем шаге мы отправили некоторое количество потока из текущей вершины в следующую, а теперь при желании можем вернуть это же количество потока обратно в текущую.
Возвращаемся обратно к нахождению пути в остаточной сети после модификации.
Разбор конкретного примера
Разобьем одну итерацию проведения потока по выбранному пути на маленькие шаги, чтобы визуально стало понятно, как меняется остаточная сеть после проталкивания очередного потока.
Допустим наш алгоритм нашел следующий путь из вершинывнашей остаточной сети, которая на момент начала, совпадает с исходным графом.
Сколько потока можем провести по этому пути.
— Больше 2 ед. мы никак не сможем пустить, пропускаем наш поток по этим рёбрам из истока в сток.
Получаем следующее:
Рёбра с нулевым весом можно удалять. Таким образом, на первой итерации мы смогли увеличить максимальный поток на 2 ед.
Теперь дело за малым, остается всего лишь итерироваться до тех пор, пока существует путь из в .
Допустим, на 2-ой итерации мы нашли такой путь в нашей остаточной сети:
Пропускаем 3 ед . потока по этому пути, и перестраиваем остаточную сеть.
Получаем следующее:
На 3-ей итерации нашли такой путь в нашей модифицированной остаточной сети:
Пускаем 1 ед. потока по этому пути и перестраиваем нашу остаточную сеть.
Получим следующую картину:
На 4-ой итерации находим следующий путь в остаточной сети:
Пускаем 4 ед. потока по этому пути и перестраиваем нашу остаточную сеть.
Получим следующую картину:
Итоговая остаточная сеть
На этом этапе наш алгоритм прекратит выполнение из-за того, что пути из истока в сток не существует. И ответом к поставленной задаче будет служить сумма потоков всех найденных увеличивающихся путей.
Ответ: 10 ед.
Спасибо большое за внимание, надеюсь, был полезен!
Буду рад любым отзывам или поправкам для повышения доступности изложения материала!
Максимальный поток и минимальный разрез
Теорема Форда-Фалкерсона 1 (о максимальном потоке и минимальном разрезе).
В любой сети существует максимальный поток. Величина максимального потока равна пропускной способности минимального разреза.
Теорема Форда-Фалкерсона 2.
Поток, вычисленный с помощью алгоритма Форда-Фалкерсона имеет максимальную величину, а разрез , где -множество вершин, помеченных при последнем помечивании, имеет минимальную пропускную способность.
Нахождение максимального потока и построение минимального разреза в сети с использованием алгоритма Форда-Фалкерсона
В данной задаче основным параметром на дугах сети является – пропускная способность. Пропускная способность показывает, сколько единиц потока может быть передано по дугам сети. Таким образом, потоком в сетиD = [N, M] называется неотрицательная вещественная функция, удовлетворяющая условиям:
1. ограниченности: поток по любой дуге сети не превосходит пропускной способности этой дуги ;
2. сохранения: суммарный поток, заходящий в любую вершину сети (кроме истока и стока), равен суммарному потоку, выходящему из этой вершины.
Дуга сети называется насыщенной, если поток по этой дуге равен пропускной способности этой дуги, т. е. .
Разрезом сетиназывается множество дуг, удаление которых из сети приводит к тому, что исток и сток оказываются несвязанными.
Пропускной способностью разрезаназывается число, равное сумме пропускных способностей дуг этого разреза. Разрез называется минимальным, если имеет наименьшую пропускную способность.
Отыскание минимального разреза – одна из основных задач анализа транспортных сетей. В силу конечности графа минимальный разрез может быть найден перебором всех разрезов, но этот путь, конечно, неприемлем для достаточно больших графов.
Минимальный разрез можно отыскать при помощи теоремы Форда – Фалкерсона: в любой транспортной сети величина любого максимального потокаравна пропускной способности любого минимального разреза.
Для нахождения максимального потока в сети разработан алгоритм Форда – Фалкерсона. Перед началом выполнения алгоритма все вершины сети нумеруются произвольным образом, кроме источника и стока (источник получает минимальный номер 1, сток – максимальный , где – число узлов).
Алгоритм состоит из следующих основных шагов:
1. Определить начальный поток в сети, сложив потоки по дугам, выходящим из источника.
2. Вершинам сети присвоить целочисленные метки, а дугам – знаки «+» и «–» по следующим правилам:
а) вершине-истоку присвоить метку ;
б) находим непомеченнуювершину , смежную помеченнойвершине . Если поток по соединяющей вершины дуге меньше пропускной способности этой дуги, то происходит помечивание, иначе переходим к рассмотрению следующей вершины. Если вершина является образомпомеченной вершины , то происходит прямое помечивание (дуга в прямом направлении допустима): вершина получает метку, равную номеру вершины , соединяющая вершины дуга получает метку «+», переходим к рассмотрению следующей вершины. Если вершина не имеет ни одного помеченного прообраза, поток по дуге в прямом направлении больше 0, то происходит обратное помечивание (дуга допустима в обратном направлении): вершина получает метку, равную номеру вершины (являющейся в данном случае ее образом), соединяющая вершины дуга получает метку «–», происходит переход к рассмотрению следующей вершины. Процесс помечивания продолжается до тех пор, пока все удовлетворяющие этим условиям вершины не получат метку.
3. Если в результате процедуры помечивания вершина-сток метки не получила, то текущий поток – максимальный, переход к шагу 5. В противном случае перейти к пункту 4.
4. Рассмотреть последовательность вершин L, метка каждой из которых равна номеру следующей за ней вершины, и множество дуг МL, соединяющих соседние вершины из L.
Построение нового потока по схеме:
а) Если дуга принадлежит множеству МL (смотри выше) и имеет знак «+», то новый поток по этой дуге = старый поток по этой дуге + Δ (схему нахождения смотри далее).
б) Если дуга принадлежит множеству МL и имеет знак «–», то новый поток по этой дуге = старый поток по этой дуге – Δ.
в) Если дуга не принадлежит множеству МL, то поток по дуге оставляем без изменения.
I. , где для нахождения рассматриваются все дуги, принадлежащие множеству МL и имеющие знак «+», и для каждой такой дуги вычисляется разность между пропускной способностью дуги и потоком по этой дуге ( ). Затем из этих значений разностей выбирается минимальное значение и присваивается .
II. Для нахождения рассматриваются все дуги, принадлежащие множеству МL и имеющие знак «–». Затем из этих дуг выбирается дуга с минимальным потоком ( ), и значение потока по этой дуге присваивается .
Перейти к шагу 2.
5. Определяем максимальный поток, складывая начальный поток и все полученные изменения потока.
В оптимальном решении, т. е. когда найден максимальный поток, минимальный разрез образуется насыщенными дугами.
Дата добавления: 2019-02-22 ; просмотров: 5017 ; Мы поможем в написании вашей работы!
Перейдем к анализу алгоритма Форда-Фалкерсона, который займет целый раздел. Этот анализ даст много полезной информации не только об алгоритме, но и о задаче о максимальном потоке.
Анализ алгоритма: потоки и разрезы
Наша следующая цель — показать, что поток, возвращаемый алгоритмом Форда-Фалкерсона, имеет максимальную возможную величину для любого потока в G. Для этого мы вернемся к теме, поднятой в разделе 7.1: верхним границам для максимальной величины потока s-t, обусловленным структурой потоковой сети. Одна из таких границ уже приводилась: величина v(f) любого потока s-t не превышает Иногда эта граница приносит пользу, но иногда оказывается очень слабой. Понятие разреза поможет нам разработать более общий механизм установления верхних границ для величины максимального потока.
Рассмотрим разбиение узлов графа на два множества A и B, для которых s ∈ A и t ∈ B. Как упоминалось в разделе 7.1, любое такое разбиение устанавливает верхнюю границу для максимально возможного потока, потому что весь поток должен где-то переходить из A в B. Формально разрезомs-t называется разбиение (A, B) множества вершин V, при котором s ∈ A и t ∈ B. Пропускная способность разреза (A, В), которую мы будем обозначать с(А, В), представляет собой обычную сумму пропускных способностей всех ребер, выходящих из А:
Как выясняется, разрезы устанавливают верхнюю границу для величины потока — очень естественную и хорошо согласующуюся с нашими интуитивными представлениями. Сейчас эти рассуждения будут формализованы в серию фактов.
(7.6) Пусть f — произвольный поток s-t, а (A, В) — произвольный разрез s-t. В этом случае — v(f) = fout(A) – fin(A).
На самом деле это утверждение намного сильнее простой верхней границы. Оно говорит, что по величине потока f, передаваемой через разрез, можно точно измерить величину потока: это общая величина, выходящая из A, за вычетом величины, которая “втекает обратно” в A. Утверждение выглядит вполне естественно, хотя чтобы доказать его, придется немного потрудиться с суммами.
Доказательство. По определению v(f) = fout(s). Из предположения следует fin(s) = 0, так как источник s не имеет входных ребер, и мы можем записать v(f) = fout(s) – fin(s). Кроме s, все узлы v в A являются внутренними, и мы знаем, что fout(v) – fin(v) = 0 для всех таких узлов. Следовательно,
так как у единственного ненулевого слагаемого в этой сумме v содержит s.
Попробуем переписать правую часть суммы. Если у ребра e оба конца принадлежат A, то f(e) один раз входит в сумму со знаком “+”, и один раз со знаком “-”; эти два слагаемых компенсируются. Если у e в A входит только начальный узел, то f(e) входит в сумму только один раз со знаком “+”. Если у e в A входит только конечный узел, то f(e) входит в сумму только один раз со знаком “-”. Наконец, если у e ни один из концов в A не входит, то f (e) вообще не встречается в сумме. С учетом этого факта имеем
Объединяя эти два уравнения, приходим к формуле из (7.6). ■
Если A = {s}, то fout(A) = fout(s), и fin(A) = 0, так как по предположению никакие ребра не входят в источник. Следовательно, утверждение для этого множества A = {s} в точности совпадает с определением величины потока v(f).
Для разреза (A, B) ребра, входящие в B, в точности совпадают с ребрами, выходящими из A. Аналогичным образом ребра, выходящие из B, в точности совпадают с ребрами, входящими в A. Следовательно, fout(A) = fin(B) и fin(A) = fout(B) просто из сравнения определений этих двух выражений. Это позволяет переформулировать (7.6) следующим образом:
(7.7) Пусть f — произвольный поток s-t, а (А, В) — произвольный разрез s-t. В этом случае v(f) = fin(B) – fout(B).
Если установить A = V — {t} и B = {t} в (7.7), получаем v(f) = fin(B) — fout(B) = fin(t) — fout(t). По предположению сток не имеет исходящих ребер, поэтому fout(t) = 0. Это означает, что величину потока также можно было бы определить в контексте стока t: это fin(t), величина потока, поступающего в сток.
Очень полезным следствием (7.6) является следующая верхняя граница.
(7.8) Пусть f — любой поток s-t, а (A, B) — любой разрез s-t. В этом случае v(f) ≤ c(A, B).
Доказательство.
Первая строка — это просто (7.6); переходим от первой строки ко второй, так как fin(A) ≥ 0, а от третьей к четвертой — применяя ограничения пропускной способности к каждому из слагаемых суммы. ■
В некотором смысле утверждение (7.8) выглядит слабее, чем (7.6), так как в нем содержится неравенство вместо равенства. Тем не менее оно чрезвычайно полезно для нас, так как его правая часть не зависит ни от какого конкретного потока f. Фактически (7.8) говорит, что величина любого потока ограничена сверху емкостью любого разреза. Другими словами, рассматривая любой разрез s-t в G с некоторой величиной с* мы немедленно знаем из (7.8), что в G не может быть потока s-t с величиной, превышающей с*. И наоборот, рассматривая любой поток s-t в G с величиной v*, можно сразу утверждать по (7.8), что в s-t не может быть разреза с величиной менее v*.
Анализ алгоритма: максимальный поток равен минимальному разрезу
Обозначим f поток, возвращаемый алгоритмом Форда-Фалкерсона. Требуется показать, что f имеет максимальную возможную величину среди всех потоков в G; для этого мы воспользуемся методом, упоминавшимся выше: предоставим разрез s-t (A*, B*), для которого v(f) = c(A*, B*). Тем самым немедленно устанавливается, что f имеет максимальную величину среди всех потоков и что (A*, B*) имеет минимальную пропускную способность по всем разрезам s-t.
Алгоритм Форда-Фалкерсона завершается, когда поток f не имеет пути s-t в остаточном графе Gf. Как выясняется, это единственное свойство, необходимое для доказательства его максимальности.
(7.9) Если f — такой поток s-t, для которого не существует пути s-t в остаточном графе Gf, то в G существует разрез s-t (A*, B*), для которого v(f) = c(A*, B*). Соответственно f имеет максимальную величину среди всех потоков в G, а (A*, B*) имеет минимальную емкость по всем разрезам s-t в G.
Доказательство. Это утверждение заявляет о существовании разреза, обладающего неким желательным свойством; теперь нужно найти такой разрез. Обозначим A* множество всех узлов v в G, для которых в Gf существует путь s-v. Множество всех остальных узлов обозначается B*: B* = V — A*.
Сначала установим, что (A*, B*) действительно является разрезом s-t. Безусловно, это разбиение V. Источник s принадлежит A*, потому что путь из s в s всегда существует. Кроме того, t ∉ A* по предположению об отсутствии пути s-t в остаточном графе; следовательно, t ∈ B*, как и требуется.
Затем предположим, что e = (u, v) является ребром в G, для которого u ∈ A* и v ∈ B* как показано на рис. 7.5. Можно утверждать, что f(e) = ce. Если бы это было не так, то e было бы прямым ребром в остаточном графе Gf, а поскольку u ∈ A*, в Gf существует путь s-u; присоединяя e к этому пути, мы получаем путь s-v в Gf, что противоречит предположению о v ∈ B*.
Рис. 7.5. Разрез (A*, B*) в доказательстве (7.9).
Теперь предположим, что e’ = (u’, v’) является ребром в G, для которого u’ ∈ B* а v’ ∈ A*. Можно утверждать, что f(e’) = 0. Если бы это было не так, то ребро e’ породило бы обратное ребро e» = (v’, u’) в остаточном графе Gf, а поскольку v’ ∈ A* в Gf существует путь s-v’; присоединяя e» к этому пути, мы получаем путь s-u’ в Gf, что противоречит предположению о u’ ∈ B*.
Итак, все ребра из A* полностью насыщены потоком, а все ребра, направленные в A*, совершенно не используются. Теперь мы можем воспользоваться (7.6), чтобы прийти к нужному выводу:
Оглядываясь назад, мы видим, почему два типа остаточных ребер — прямые и обратные — критичны для анализа двух слагаемых в выражении из (7.6).
Так как алгоритм Форда-Фалкерсона завершается при отсутствии пути s-t в остаточном графе, из (7.6) немедленно следует его оптимальность.
(7.10) Поток f возвращаемый алгоритмом Форда-Фалкерсона, является максимальным.
Также заметим, что наш алгоритм легко расширяется для вычисления минимального разреза s-t (A*, B*).
(7.11) Для заданного потока f с максимальной величиной разрез s-t с минимальной пропускной способностью вычисляется за время O(m).
Доказательство. Просто последуем за построением доказательства (7.9). Мы строим остаточный граф Gf и проводим поиск в ширину или поиск в глубину для определения множества A* всех узлов, доступных из s. После этого мы определяем B* = V — A* и возвращаем разрез (A*, B*). ■
Обратите внимание: в графе G может быть много разрезов с минимальной пропускной способностью; процедура в доказательстве (7.11) просто находит один из этих разрезов, начиная с максимального потока f.
Дополнительно анализ алгоритма выявил следующий поразительный факт:
(7.12) В каждой потоковой сети существует поток f и разрез (A, B), для которых v f) = c(A, B).
Суть в том, что f в (7.12) должен быть максимальным потоком s-t; если бы существовал поток f’ с большей величиной, то значение f’ превысило бы пропускную способность (A, B), а это противоречит (7.8). Аналогичным образом можно сделать вывод о том, что (A, B) в (7.12) является минимальным разрезом (никакой другой разрез не может иметь меньшую пропускную способность), потому что если бы существовал разрез (A’, B’) с меньшей пропускной способностью, он был бы меньше величины f, а это снова противоречит (7.8). Из-за этих следствий утверждение (7.12) часто называется теоремой о максимальном потоке и минимальном разрезе, и формулируется следующим образом.
(7.13) В любой потоковой сети максимальная величина потока s-t равна минимальной пропускной способности разреза s-t.
Дальнейший анализ: целочисленные потоки
Среди многочисленных следствий нашего анализа алгоритма Форда-Фалкерсона есть одно особенно важное. Согласно (7.2) в любой момент времени величина потока остается целочисленной, а согласно (7.9) в итоге формируется максимальный поток. Следовательно:
(7.14) Если все пропускные способности потоковой сети являются целыми числами, то существует максимальный поток, для которого каждая величина потока f(e) также является целым числом.
Обратите внимание: (7.14) не утверждает, что каждый максимальный поток является целочисленным, а лишь то, что некоторый максимальный поток обладает этим свойством. Интересно, что в (7.14) алгоритм Форда-Фалкерсона никак не упоминается, но наш алгоритмический подход предоставляет, пожалуй, самый простой способ доказательства этого утверждения.
Вещественные числа как пропускные способности
Наконец, прежде чем двигаться дальше, зададимся вопросом, насколько критичным было предположение о целочисленности пропускных способностей (речь не идет о (7.4), (7.5) и (7.14), где оно было очевидно необходимо). Для начала стоит заметить, что если разрешить использование рациональных чисел в качестве пропускных способностей, ситуация не станет более общей, потому что мы можем определить наименьшее общее кратное всех пропускных способностей и умножить их все на это значение, чтобы получить эквивалентную задачу с целочисленными пропускными способностями.
А если пропускные способности будут задаваться вещественными числами? Где в доказательстве мы использовали тот факт, что пропускные способности являются целыми числами? Да, использовали, и он был весьма критичен: утверждение (7.2) использовалось для доказательства того, что в (7.4) величина потока увеличивается по крайней мере на 1 при каждом шаге. С вещественными пропускными способностями следует учесть, что величина потока может возрастать со все более малыми приращениями; следовательно, пропадает гарантия конечности количества итераций цикла. И эта проблема оказывается очень серьезной, потому что при аномальном выборе увеличивающего пути алгоритм Форда-Фалкерсона с вещественными пропускными способностями может выполняться бесконечно.
Однако можно доказать, что теорема о максимальном потоке и минимальном разрезе (7.12) остается истинной даже в том случае, если пропускные способности являются вещественными числами. Утверждение (7.9) предполагало лишь то, что поток f не имеет пути s-t в остаточном графе Gf, чтобы сделать вывод о существовании разреза s-t с равной величиной. Очевидно, для любого потока f с максимальной величиной остаточный граф не содержит пути s-t; в противном случае величину потока можно было бы увеличить. Следовательно, чтобы доказать (7.12) для случая вещественных пропускных способностей, достаточно показать, что в каждой потоковой сети существует максимальный поток.
Конечно, при любом практическом применении потоков пропускные способности будут целыми или вещественными числами. Однако проблема аномального выбора увеличивающего пути может проявиться даже с целыми пропускными способностями: из-за нее алгоритм Форда-Фалкерсона может потребовать огромного количества итераций.
В следующем разделе показано, как выбрать увеличивающие пути так, чтобы избежать потенциально нежелательного поведения алгоритма.