Как найти разрешающий коэффициент

1. Определение общего, базисного и частного решений.

Решение системы, получающееся при
задании конкретных значений свободных
переменных, называется частным
решением системы.

Решение системы, в котором все свободные
переменные полагаются равными нулю,
называется базисным

(количество возможных базисных решений
равно количеству вариантов определения
базисных переменных).

Равенства, выражающие базисные переменные
через свободные, называются общим
решением системы.

1. Определение допустимого, опорного и невырожденного решений.

Опорное решение называется невырожденным,
если оно содержит положительных
компонент (по числу ограничений).

, для нахождения начального допустимого
решения необходимо, чтобы в каждое из
уравнений входила переменная с
коэффициентом 1 и не входила в другие
уравнения (базисная переменная).

1. Правила выбора разрешающего столбца, разрешающей строки и разрешающей: элемента

Выбор разрешающего элемента. Если
при поиске минимума в строке целевой
функции есть коэффициенты больше нуля,
то выбираем столбец с положительным
коэффициентом в строке целевой функции
в качестве разрешающего. Пусть это
столбец с номером .

Для выбора разрешающей строки (разрешающего
элемента) среди положительных коэффициентов
разрешающего столбца выбираем тот (ту
строку), для которого отношение
коэффициента в столбце свободных членов
к коэффициенту в разрешающем столбце
минимально:

.

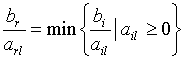
– разрешающий (направляющий) элемент,
строка

– разрешающая

Правила выбора разрешающего элемента

1.При условии отсутствия “0-строк”
(ограничений-равенств) и “сво­бодных”
перемен­ных (т.е. переменных, на которые
не наложено требование неотри­цатель­ности).

Если в столбце свободных членов
симплексной таблицы нет отрицательных
элементов, то опорный план найден.

Есть отрицательные элементы в столбце
свободных членов, например . В такой
строке ищем отрицательный коэф­фициент
, и этим самым определяем разрешающий
столбец . Если не найдем отри­цательный
, то система ограничений несовместна
(противо­речива).

В качестве разрешающей выбираем строку,
которой соответствует минимальное
отношение:

,

где

— номер разрешающей строки. Таким образом,

— разрешающий элемент.

После того, как разрешающий элемент
найден, делаем шаг модифицированного
жорданова исключения с направляющим
элементом и переходим к следующей
симплексной таблице.

2. В случае присутствия ограничений-равенств
и “свободных” переменных поступают
следующим образом.

Выбирают разрешающий элемент в “0-строке”
и делают шаг модифицированного жорданова
исключения, после чего вычеркивают этот
разрешающий столбец. Данную
последовательность действий продолжают
до тех пор, пока в симплексной таблице
остается хотя бы одна “0-строка” (при
этом таблица сокращается).

Если же присутствуют и свободные
переменные, то необходимо данные
переменные сделать базисными. И после
того, как свободная переменная станет
базисной, далее в процессе определения
разрешающего элемента при поиске
опорного и оптимального планов данная
строка не учитывается (но преобразуется).

Для этого выбирают любой из отрицательных
элементов столбца свободных членов
(пусть это будет b₂ < 0 ) и
просматривают элементы строки, в которой
он находится. В этой строке выбирают
любой отрицательный элемент и
соответствующий ему столбец определит
переменную (например x_l ), которую
следует исключить из небазисных и ввести
в базис на следующем шаге. Столбец,
соответствующий переменной x_l ,
называется ведущим, или
разрешающим. Если в строке с
отрицательным свободным членом нет
отрицательных элементов, то система
ограничений несовместна и задача не
имеет решения.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Управление производством предполагает постоянное принятие решений. Каждое принятое решение выбирается из определенного множества допустимых альтернатив. Задача менеджмента в данном случае состоит в том, чтобы выбрать оптимальное решение, то есть то решение, которое по определенным признакам предпочтительнее остальных. Решение будет считаться оптимальным, если оно приведет к максимально возможному положительному эффекту (например, росту прибыли предприятия).

Одним из методов, позволяющих найти оптимальное решение среди всего множества допустимых решений, является исследование операций. Исследование операций — один из разделов прикладной математики, суть которого заключается в поиске максимума (минимума) целевой функции, с учетом всех имеющихся ограничений. Суть экономики предприятия заключается в максимизации прибыли, с учетом ограниченности ресурсов, которыми располагает организация. Этим обусловлена применимость методов исследования операций в решении задач организации производственного процесса на предприятии. В экономике предприятия такие задачи называются задачами распределения ресурсов (или задачами оптимизации).

Рассмотрим пример, как можно применять методы исследования операций для решения производственных задач и как можно ускорить данный процесс путем применения встроенных возможностей MS Excel.

Предположим, автосервисное предприятие разработало для клиентов сезонные стимулирующие акции, суть которых заключается в том, что клиент, заплатив фиксированную сумму, получает целый пакет услуг по подготовке автомобиля к летнему сезону. Всего клиентам предложено два вида пакетов услуг:

1) пакет «Чистое стекло» стоимостью 3600 руб., в который входит комплекс работ по диагностике и осмотру автомобиля, очистка внутренней поверхности стекол автомобиля с применением специального спрея (плюс один флакон спрея в подарок); заливка в омывательный бачок стеклоочищающей жидкости (плюс одна бутыль стеклоочищающей жидкости в подарок);

2) пакет «Свежий воздух» стоимостью 4300 руб., в который входит комплекс работ по диагностике и осмотру автомобиля, включая работы по очистке и дезинфекции кондиционера автомобиля с применением специального средства; очистка внутренней поверхности стекол автомобиля с применением специального спрея; заливка в омывательный бачок стеклоочищающей жидкости.

В табл. 1 представлен комплекс работ по диагностике и осмотру автомобиля (количество нормо-часов).

Таким образом, данные два пакета услуг отличаются друг от друга тем, что в первый пакет дополнительно входит подарок в виде одного флакона спрея для внутренней очистки стекол и одной бутыли стеклоочищающей жидкости, а во второй — проведение работ по очистке и дезинфекции кондиционера с применением специального средства.

Проведение сезонных акций позволяет предприятию решить целый ряд задач:

1. Привлечение клиентов.

2. Сбыт залежавшихся сезонных товаров (автохимия).

3. Загрузка механиков.

4. Получение дополнительной прибыли.

По задумке менеджмента организации, количество пакетов ограничено:

• во-первых, акция будет продолжаться до тех пор, пока не кончатся складские остатки участвующей в акции автохимии;

• во-вторых, срок проведения акции органичен одним месяцем (апрелем);

• в-третьих, на выполнение сервисных мероприятий могут быть задействованы только четыре механика.

Таким образом, ресурсы, выделяемые на проведение данной акции, ограничены. Ограничения по ресурсам на проведение сезонной акции представлены в табл. 2.

На проведение сезонной акции может быть выделено не более:

• 320 флаконов спрея для очистки внутренней поверхности стекла;

• 260 бутылей стеклоомывающей жидкости;

• 150 бутылей жидкости для очистки и дезинфекции кондиционера.

К тому же ограничено время работы механиков: в апреле 22 рабочих дня, продуктивный рабочий день механика — 7 ч в день. Следовательно, располагаемый фонд рабочего времени четырех механиков равен 616 ч (4 × 22 × 7).

Всего на один пакет «Чистое стекло» необходимо затратить:

• 2,5 ч работы механика;

• 2 флакона спрея для очистки внутренней поверхности стекла (один использовать, один — в подарок);

• 2 бутыли стеклоомывающей жидкости (одну использовать, одну — в подарок).

На пакет «Свежий воздух» необходимо затратить:

• 3,6 ч работы механика;

• 1 флакон спрея для очистки внутренней поверхности стекла;

• 1 бутыль стеклоомывающей жидкости и одну бутыль жидкости для очистки и дезинфекции кондиционера.

Ограничение по ресурсам является одним из условий задачи исследования операций. Характерной особенностью исследования операций является системный подход. В связи с этим существующие ограничения по ресурсам можно представить в виде системы уравнений. Для начала введем обозначения для переменных нашей задачи:

• X1 — количество пакетов «Чистое стекло»;

• Х2 — количество пакетов «Свежий воздух»;

• A — количество часов механика;

• B — количество флаконов спрея для внутренней очистки стекол;

• C — количество бутылей стеклоомывающей жидкости;

• D — количество бутылей жидкости для очистки и дезинфекции кондиционеров.

Далее нужно определиться с ограничениями, которым должны удовлетворять переменные нашей задачи:

1) во-первых, количество пакетов не может быть отрицательным: Х1, Х2 ≥ 0;

2) во-вторых, расход ресурсов не должен превышать имеющиеся запасы. Это можно выразить при помощи неравенств:

• по ресурсу А: 2,5 × Х1 + 3,6 × Х2 ≤ 616;

• по ресурсу В: 2 × Х1 + 1 × Х2 ≤ 320;

• по ресурсу С: 2 × Х1 + 1 × Х2 ≤ 260;

• по ресурсу D: 0 × Х1 + 1 × Х2 ≤ 150.

Затем следует определиться с целевой функцией (направлением для оптимизации). Логично было бы распределить квоту на оказание пакетов услуг таким образом, чтобы предприятие получило максимальную прибыль. Для этого нужно рассчитать, сколько прибыли приносит продажа одного пакета услуг, то есть сопоставить цену реализации пакета и стоимость затрачиваемых ресурсов. Как уже говорилось выше, стоимость пакета «Чистое стекло» составляет 3600 руб., а пакета «Свежий воздух» — 4300 руб. Данные суммы необходимо сопоставить с затратами на выполнение услуг:

• тарифная часовая ставка механика составляет 350 руб. за нормо-час (включая налоги и взносы с ФОТ);

• стоимость флакона жидкости для очистки внутренней поверхности стекла — 661 руб.;

• стоимость бутыли стеклоочищающей жидкости — 250 руб.;

• стоимость бутыли жидкости для очистки и дезинфекции кондиционеров — 1589 руб.

Расчет прибыли от реализации каждого из пакетов на основании имеющихся данных представлен в табл. 3.

Итак, продажа одного пакета «Чистое стекло» принесет предприятию 903 руб. прибыли, а пакета «Свежий воздух» — 540 руб.

Целевая функция (Z) в данном случае примет вид:

Z = 903 × Х1 + 540 × Х2.

Задача — найти максимум целевой функции с учетом существующих ограничений:

• 2,5 × Х1 + 3,6 × Х2 ≤ 616;

• 2 × Х1 + 1 × Х2 ≤ 320;

• 2 × Х1 + 1 × Х2 ≤ 260;

• 1 × Х2 ≤ 150;

• Х1, Х2 ≥ 0.

Решим эту задачу, используя симплекс-метод. Симплекс-метод представляет собой алгоритм решения оптимизационной задачи линейного программирования путем перебора вершин выпуклого многогранника в многомерном пространстве. Дело в том, что представленная система уравнений имеет бесконечное множество решений. Если представить это множество графически, то получится многогранник, в одной из вершин которого находится оптимальное решение. Симплекс-метод как раз и заключается в нахождении исходной вершины множества допустимых решений, в последовательном переходе от одной вершины к другой, ведущий к оптимизации значения целевой функции.

Для решения нашей задачи симплекс-методом ее нужно привести к так называемому стандартному виду: преобразовать неравенства нашей системы ограничений в равенства, добавив в левую часть каждого из уравнений неотрицательные числа (назовем их Х3, Х4, Х5 и Х6), которые называются балансовыми переменными (переменные Х1 и Х2 называются свободными). Получится следующая система уравнений:

• 2,5 × Х1 + 3,6 × Х2 + Х3 = 616;

• 2 × Х1 + 1 × Х2 + Х4 = 320;

• 2 × Х1 + 1 × Х2 + Х5 = 260;

• 1 × Х2 + Х6 = 150;

• Х1, Х2, Х3, Х4, Х5, Х6 ≥ 0.

Решить поставленную задачу симплекс-методом удобнее всего с помощью симплекс-таблицы. Этапы поиска оптимального решения следующие:

построение первой симплекс-таблицы;

последовательное преобразование симплекс-таблиц по определенному алгоритму, до выполнения определенных условий.

Последовательное преобразование симплекс-таблиц и будет означать переход из одной точки множества допустимых решений в другую, до тех пор, пока не будет найдено оптимальное решение. Прежде чем составить первую симплекс-таблицу, необходимо преобразовать целевую функцию в следующий вид:

Z – 903 × Х1 – 540 × Х2 = 0.

Теперь строим первую симплекс-таблицу. Столбцами будут переменные Х1–Х6, а строками — имеющиеся ресурсы (А, В, С, D). На пересечении строки и столбца находятся коэффициенты перед переменными по каждому виду ресурса в нашей системе ограничений. Так, по строке А (время работы механиков) в столбце Х1 будет стоять коэффициент 2,5; в столбце Х2 — 3,6; в столбце Х3 — 1, а в Х4–Х6 — 0.

Также вводится дополнительный столбец (назовем его b), в котором стоят ограничения по каждому из ресурсов. После этого вводится дополнительная строка Е, в которой содержатся коэффициенты в нашей целевой функции (Z – 903 × Х1 – 540 × Х2 = 0). Получилась следующая симплекс-таблица, представленная в табл. 4.

Значение функции Z равно числу, стоящему в правом нижнем углу табл. 4. Последующее преобразование симплекс-таблицы связано с выбором разрешающей строки и разрешающего столбца.

Разрешающим столбцом является тот столбец, у которого коэффициенты в целевой функции (строка Е) являются отрицательными и наибольшими по модулю. В данной таблице это будет столбец Х1, у которого по строке Е стоит значение –903. Следует заметить, что преобразование симплекс-таблиц будет происходить до тех пор, пока в строке Е не останется отрицательных значений.

Теперь нужно найти разрешающую строку. Она определяется путем нахождения минимального отношения коэффициентов в столбце b к соответствующим коэффициентам разрешающего столбца (за исключением нулевых и отрицательных элементов, по которым соотношение не определяется).

Для нашей первой симплекс-таблицы разрешающей будет строка С, так как именно в ней наименьшее соотношение элемента столбца b и элемента разрешающего столбца Х1 (260 / 2 = 130). Элемент таблицы, который находится на пересечении разрешающего столбца и разрешающей строки, называется разрешающим элементом (в табл. 4 ячейка данного элемента выделена цветом).

После нахождения разрешающего элемента производится процедура симплекс-преобразования. Цель данной процедуры — сделать разрешающий элемент равным единице, а все остальные элементы разрешающего столбца — нулевыми.

Преобразование осуществляется определенными методами:

1) разрешающую строку можно делить и умножать на любое число;

2) к любой строке можно прибавлять или отнимать соответствующие элементы разрешающей строки, поделенные или умноженные на любое число.

Выполним предложенные преобразования. Чтобы приравнять разрешающий элемент к единице, разделим все элементы разрешающей строки на 2. Затем из элементов строки А отнимем элементы разрешающей строки С, умноженные на 2,5. Далее из элементов строки В отнимем элементы разрешающей строки С, умноженные на 2. Со строкой D никаких преобразований не производим (в разрешающем столбце итак стоит нулевое значение). К элементам строки Е прибавляем элементы разрешающей строки С, умноженные на 903. Получилась вторая симплекс-таблица, которая представлена в табл. 5.

Повторяем ту же процедуру, что и с табл. 4. Для начала находим разрешающий столбец (с наибольшим по модулю отрицательным коэффициентом перед целевой функцией). Разрешающим в данном случае будет столбец Х2. Далее находим разрешающую строку. Это будет строка А, так как для нее выполняется условие минимальности соотношения элемента столбца b к соответствующему элементу разрешающего столбца Х2 (291 / 2,35 = 123,83).

Элемент на пересечении строки А и столбца Х2 будет разрешающим. Выполняем преобразование разрешающего элемента в единицу, а остальных элементов столбца Х2 в нули. Все элементы строки А делим на 2,35. Со строкой В никаких преобразований не производим (в разрешающем столбце и так стоит нулевое значение). Из элементов строки С отнимем элементы разрешающей строки А, умноженные на 0,5 и деленные на 2,35. Из элементов строки D отнимем элементы разрешающей строки А, деленные на 2,35. К элементам строки Е прибавляем элементы разрешающей строки А, умноженные на 88,5 и деленные на 2,35. Получилась третья симплекс-таблица, которая представлена в табл. 6.

В полученной симплекс-таблице в строке Е, содержащей коэффициенты целевой функции, нет отрицательных значений, следовательно вычисление завершено. Значения переменных Х1 и Х2 расположены в столбце b на тех строках, в которых в столбцах Х1 и Х2 стоят единицы. Соответственно, Х1 = 68,0851, а Х2 = 123,8298. Значение целевой функции при таких переменных будет равно:

Z = 903 × 68,0851 + 540 × 123,8298 = 128 348,94.

Полученная сумма — это максимальная прибыль предприятия от продажи пакетов. Однако следует заметить, что при решении поставленной задачи не была учтена одна существенная оговорка. Дело в том, что количество проданных сезонных пакетов может быть лишь целым числом (автосервис не может продать часть пакета услуг).

Существует ряд приемов, которые позволяют вводить в задачу оптимизации условие целочисленности переменных за счет ввода дополнительных ограничений системы. Однако современному специалисту проще решать данную задачу, используя инструмент MS Excel — «Поиск решения», который позволяет не только находить оптимальное решение задачи, но и делать его таковым, чтобы оно удовлетворяло условию целочисленности переменных.

Покажем это на наглядном примере. Для начала следует ввести все данные задачи в рабочий лист MS Excel (рис. 1).

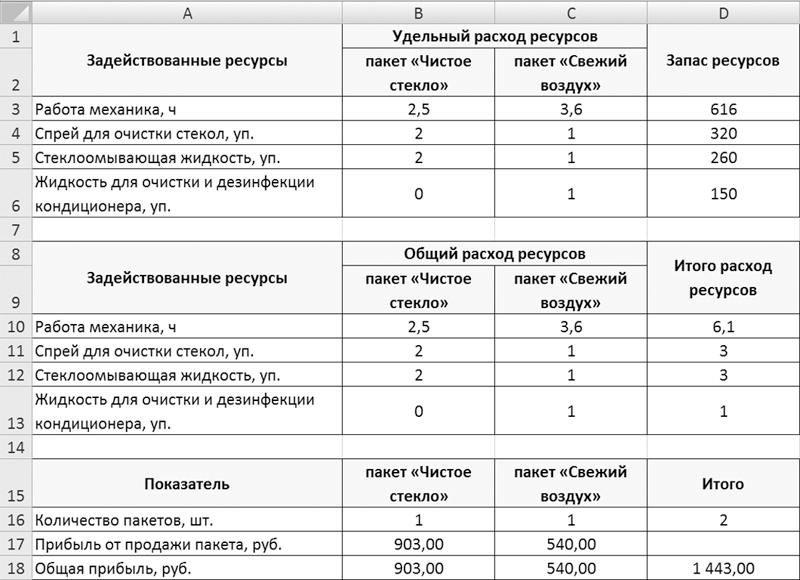
Рис. 1. Ввод данных задачи оптимизации в MS Excel

Сначала следует ввести нормативы расхода имеющихся ресурсов на каждый из пакетов:

• в ячейки B3:B6 вводятся нормативы расхода всех ресурсов на продажу одного пакета «Чистое стекло»;

• в ячейки C3:C6 вводятся нормативы расхода всех ресурсов на продажу одного пакета «Свежий воздух»;

• в ячейки D3:D6 заносят запасы (лимиты расхода) по каждому из ресурсов.

Для того чтобы посчитать общий расход ресурсов и соотнести его с запасами, необходимо ввести данные о количестве проданных пакетов (ячейки В16 и С16). Для начала проставим там единичные значения (как будто продано по одному сезонному пакету). Общий расход ресурсов рассчитывается в диапазоне ячеек A8:D13, в котором количество проданных пакетов (ячейки В16 и С16) умножается на норматив расхода (диапазоны B3:B6 и C3:C6). В диапазоне D10:D13 рассчитывается суммарный расход по каждому из ресурсов.

Так, например, расход нормо-часов механиков по пакету «Чистое стекло» производится в ячейке В10 путем умножения значений ячейки В16 (количество проданных пакетов «Чистое стекло») на ячейку В3 (норматив выполнения работ по пакету «Чистое стекло»). Расход нормо-часов механиков по пакету «Свежий воздух» производится в ячейке С10 путем умножения значений ячейки С16 (количество проданных пакетов «Свежий воздух») на ячейку С3 (норматив выполнения работ по пакету «Свежий воздух»).

Итоговое значение расхода часов механиков рассчитывается в ячейке D10 путем сложения значений ячеек В10 и С10 (сумма в ячейке D10 не должна превышать лимит, установленный в ячейке D3).

Также на рабочем листе идет расчет прибыли от продажи пакетов (ячейки В18 и С18). Для этого размер прибыли от продажи одного пакета (значения проставлены в ячейках В17 и С17) умножается на количество проданных пакетов (ячейки В16 и С16). В ячейке D18 стоит итоговое значение прибыли.

Цель — максимизировать значение, рассчитываемое в ячейке D18 при соблюдении всех ограничений задачи.

Воспользуемся инструментом «Поиск решения» (находим в меню «Данные» — «Анализ»). Диалоговое окно представлено на рис. 2.

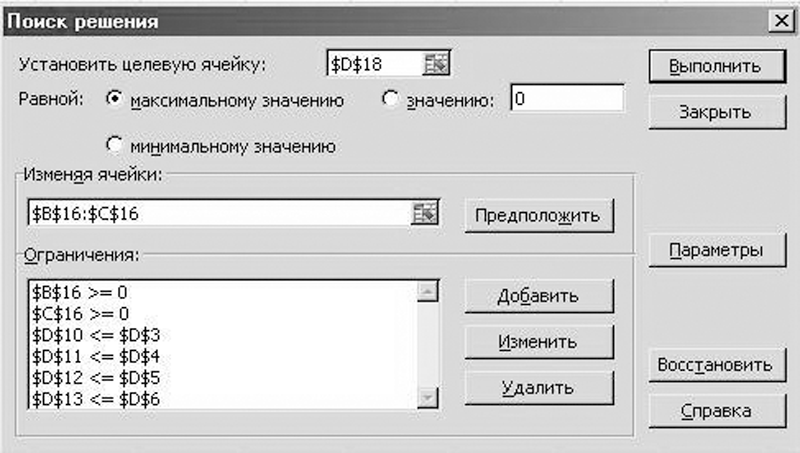
Рис. 2. Диалоговое окно инструмента «Поиск решения»

По условиям поставленной задачи необходимо установить в целевую ячейку D18 (общая прибыль от продажи пакетов) максимальное значение, изменяя ячейки В16:С16 (количество проданных пакетов «Чистое стекло» и «Свежий воздух»).

При этом должны быть прописаны все ограничения нашей задачи:

• В16 и С16 >= 0 (количество проданных пакетов неотрицательно);

• D10 <= D3 (расход нормо-часов механиков не превышает имеющийся фонд рабочего времени);

• D11 <= D4 (расход спрея для очистки стекол не превышает складских остатков);

• D12 <= D5 (расход стеклоочищающей жидкости не превышает складских остатков);

• D13 <= D6 (расход жидкости для очистки и дезинфекции кондиционеров не превышает складских остатков).

После ввода ограничений нажимаем кнопку «Выполнить». Ячейки В16 и С16 заполняются автоматически. В целевой ячейке D18 получается значение прибыли. На рис. 3 представлены результаты вычислений.

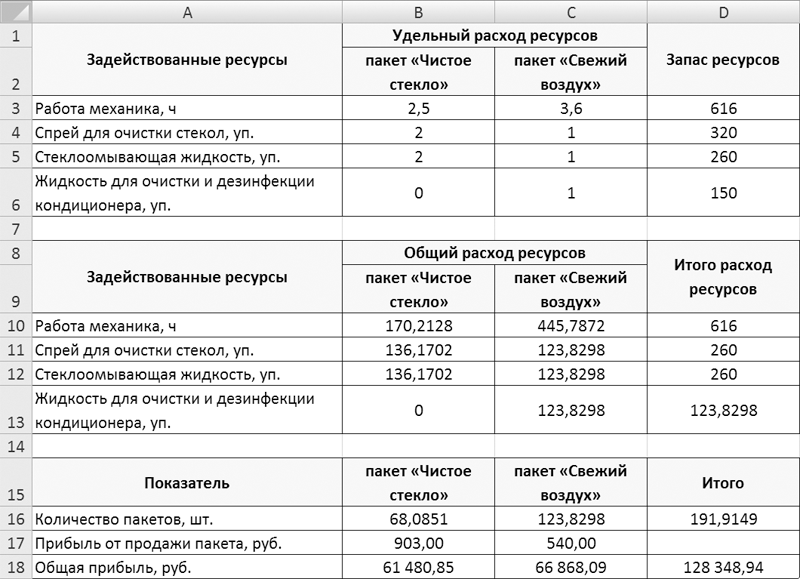
Рис. 3. Результаты вычислений

Как видно из рис. 3, результаты вычислений получились аналогичными тем, что были достигнуты при помощи симплекс-таблиц. Однако эти данные, как уже говорилось выше, не могут быть приняты по причине своей нецелочисленности. Чтобы устранить данный недостаток, необходимо в диалоговом окне инструмента «Поиск решения» прописать дополнительные условия (рис. 4).

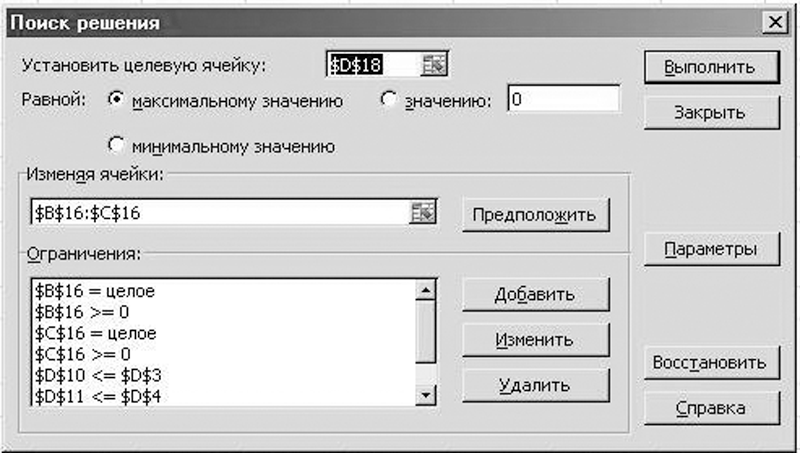
Рис. 4. Диалоговое окно инструмента «Поиск решения» с добавлением условия целочисленности

Результаты вычисления после добавления условия целочисленности показаны на рис. 5.

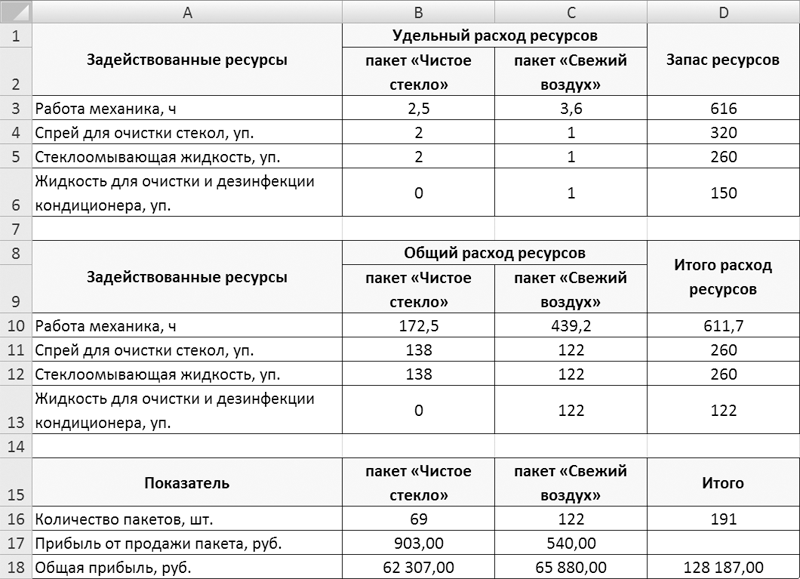
Рис. 5. Результаты вычисления после добавления условия целочисленности

Полученные данные удовлетворяют всем заданным условия. Если руководство предприятия выделит на проведение сезонной акции 69 пакетов «Чистое стекло» и 122 пакета «Свежий воздух», то за счет имеющихся в распоряжении ресурсов будет получена максимальная прибыль, которая составит 128 187 руб.

Заключение

В данной статье на простых примерах мы рассмотрели, как можно применять методы исследования операций для решения производственных задач, и выяснили, как можно ускорить данный процесс путем применения встроенных возможностей MS Excel.

СИМПЛЕКСНЫЙ МЕТОД ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ

1. Общая характеристика симплексного метода
Поскольку система линейных уравнений изучается в курсе элементарной алгебры, остановимся лишь на основных определениях, необходимых для понимания дальнейшего материала.
Если система имеет хотя бы одно решение, она называется совместной. Несовместные системы не имеют ни одного решения.

Допустимым решением называется совокупность значений n-переменных, удовлетворяющая системе ограничений и условиям не отрицательности.

Широко используемым на практике методом решения задач линейного программирования является симплексный. Этот метод решения задачи линейного программирования основан на переходе от одного опорного решения к другому, при котором значение целевой функции улучшается (на максимум — увеличивается, на минимум — уменьшается или остается на прежнем уровне), при условии, что дан­ная задача имеет оптимальный план.

При решение задачи симплексным методом можно выделить следующие стадии:

• приведение задачи к канонической форме и нахождение пер­воначального варианта допустимого плана;
• проверка найденного варианта плана на оптимальность (если полученный вариант окажется оптимальным, то решение получено, в противном случае план должен быть улучшен);
• последовательное улучшение плана в симплексных таблицах до получения оптимального.

2. Решение задачи линейного программирования в симплексных таблицах. Правила построения симплексных таблиц
Рассмотрим схему построения на примере.
Пример 1:
3Х1 + Х2 ? 4
Х1 + 3Х2 ? 4
Хj ? 0, j = 1,…,4
Zmax = 2+ Х1+2Х2.

Чтобы решить данную задачу линейного программирования симплексным методом, она должна быть представлена в канонической форме, система ограничений приведена к единичному базису, сво­бодные члены уравнений должны быть неотрицательны.

Как видим, задача не приведена к канонической форме и к единич­ному базису. Поэтому вводим дополнительные переменные Х3 и Х4.
3Х1 + Х2 + Х3 = 4
Х1 + 3Х2 + Х4 = 4
Хj ? 0, j = 1,…,4
Zmax = 2+ Х1+2Х2 + 0 * Х3 +0 * Х4

Составим первую симплексную таблицу. Она представляет собой форму выражения первого опорного плана. Коэффициенты, стоящие в Z-строке, показывают, как изменяется значение целевой функции при единичном изменении соответствующей свободной переменной. И на­зываются эти коэффициенты оценкой или индексом этой свободной пе­ременной. А сама строка Z называется индексной или оценочной.

Заполнение таблицы

• В первом столбце перечисляют базисные переменные.
• Во второй столбец записывают оценки базисных переменных, указанные в целевой функции.
• В третьем столбце указывают свободные члены.
• В остальных столбцах таблицы записывают коэффициенты при свободных переменных по соответствующим уравнениям.
• Над рабочей частью таблицы перечисляют свободные пере­менные.
• Сверху над свободными переменными помещают оценки сво­бодных переменных, указанные в целевой функции. Над столбцом свободных членов записывают свободный член целевой функции (если таковой имеется) с противоположным знаком.

Оценки Z-строки рассчитывают по формуле

(1)m
                  m
a0j = ?Ciaij – Cj
                i=1

где j = 1, 2, …, n;
аij — коэффициенты j-ого столбца;
Сi— коэффициенты при базисных переменных в уравнении Z;
Сj— коэффициенты при свободных переменных в уравнении Z.

Определение оптимальности плана. Построение новой симплексной таблицы.

В симплексных таблицах формальным признаком оптимальности является содержание оценочной строки.

Ключевая теорема симплексного метода (Z на максимум):

Если после выполнения очередной итерации:

• найдется хотя бы одна отрицательная оценка, а в столбце, где она стоит, есть хотя бы один положительный элемент, то опорное решение можно улучшить, выполнив следующую итерацию;
• найдется хотя бы одна отрицательная оценка, столбец кото­рой не содержит положительных элементов, то функция Zнеогра­ничена в области допустимых решений (Zmax > +?);
• все оценки окажутся неотрицательными, то достигнуто опти­мальное решение.

Согласно данной теореме:

• Просматриваются оценки Z — строки. Если они все неотрица­тельны, то получено оптимальное решение при решении на максимум целевой функции, если все оценки ? 0, то получено оптимальное ре­шении при решении на минимум целевой функции.
• Если оптимальное решение не получено, то выбирается разре­шающий столбец по наибольшей по абсолютной величине отрицатель­ной оценке Z-строки — при решении на максимум и по наибольшей по­ложительной оценке — при решении на минимум целевой функции.
• Составляются симплексные отношения — отношения свобод­ных членов к положительным коэффициентам разрешающего столб­ца. Минимальное из этих отношений (min{аi0,/аip}) определит раз­решающую строку. Коэффициент, находящийся на пересечении раз­решающей строки и разрешающего столбца, называется разрешаю­щим элементом.

Если в разрешающем столбце нет ни одного положительного ко­эффициента, то задача не имеет решения по причине неограниченно­сти целевой функции (Zmax > +?, Zmin > -?).

• Осуществляется переход к новой таблице, где базисная пере­менная заменяется на свободную, соответствующую разрешающему столбцу.
• Бывший разрешающий элемент заменяется обратным по вели­чине (1/ аqp).
• Все остальные элементы бывшего разрешающего столбца делят­ся на разрешающие элементы и меняют знаки на противоположные.

Если в бывшем разрешающем столбце в какой-то строке стоял «0», то эта строка переносится в следующую таблицу без изменений.

7. Все остальные элементы бывшей разрешающей строки делятся на разрешающий элемент.

Если в бывшей разрешающей строке в каком-то столбце стоял «0», то этот столбец переносится в следующую таблицу без изменений.

8. Остальные элементы таблицы пересчитываются по правилу прямоугольника:

коэф. разрешающей строки * коэф. разрешающего столбца
aij? = исходный коэффициент —                                 разрешающий элемент

9. Осуществляется контроль за правильностью расчетов для эле­ментов 2-строки по формуле (1).

10. Если ошибок нет, то алгоритм повторяется с пункта 1 .

В первой симплексной таблице нашего примера все коэффициен­ты оценочной строки отрицательны. Следовательно, согласно теоре­ме, план (на максимум целевой функции) не является оптимальным и требует улучшения. В последнем столбце рассчитывают симплексные отношения (табл. 2.1).

Таблица 2. 1
Симплексная таблица (исходное опорное решение)

Св.П Б.П.	Сj Ci	-2	1	2
ai0	X1	X2	ai0/aip
X3	0	4	3	1	4
X4	0	4	1	(3)	4/3<
Z		2	-1	-2 ^

Исходное опорное решение: X1 (0,0,4,4); Zmax = 2.

Во второй симплексной таблице (табл. 2.2.) меняем местами ба­зисную переменную Х4 и свободную Х2.

На месте бывшего разрешающего элемента запишем обратную величину, то есть 1/3.

Все остальные элементы разрешающей строки в новой таблице вычислим путем деления на разрешающий элемент: 4/3; 1/3.

Все остальные элементы бывшего разрешающего столбца опре­делим путем деления на разрешающий элемент. Результат запишем в новую таблицу с противоположным знаком: -1/3; 2/3.

Все остальные элементы таблицы вычислим по правилу прямо­угольника.

Первая строка:                                                        Оценочная строка:
4-4*1/3=8/3                                                              2-4*(-2)/3=14/3
3-1*1/3=8/3                                                              -1-1*(-2)/3=-1/3

Таблица 2. 2
Вторая симплексная таблица

Св.П Б.П.	Сj Ci	-2	1	0
ai0	X1	X4	ai0/aip
X3	0	8/3	(8/3)	-1/3	1 <
X2	2	4/3	1/3	1/3	4
Z		14/3	-1/3 ^	2/3

Проверим правильность заполнения  Z-строки по формуле (1).
а00 = 0*8/3+2*4/3-(-2)=14/3
а01 = 0*8/3+2*1/3-1=-1/3
а02 = 0*(-1/3)+2*1/3-0=2/3.
Так как в оценочной строке есть еще отрицательные оценки, оптимальное решение не получено, можем записать только опорное решение:
Х2 (0,4/3,8/3,0)  Zmax =14/3.
По тому же алгоритму пересчитываем коэффициенты третьей таблицы.

Таблица 2. 3
Третья симплексная таблица

Св.П Б.П.	Сj Ci	-2	0	0
ai0	X3	X4
X1	1	1	3/8	-1/8
X2	2	1	-1/8	3/8
Z		5	1/8	5/8

Все оценки неотрицательны, следовательно, получено оптималь­ное решение: Хопт (1,1,0,0) Zmax = 5.

Пример 2:
Задача решалась на максимум функции (Z —> мах). На последнем шаге была получена следующая таблица.

Таблица 2.4
Последняя симплексная таблица

Св.П Б.П.	Сj Ci	0	1	0
ai0	X3	X2
X1	2	2	1	-1
X4	0	1	1	-1/2
Z		4	1	-2  ^

В разрешающем столбце нет ни одного положительного элемен­та, следовательно, Zmax >+?, то есть задача линейного программи­рования не имеет решения по причине неограниченности целевой функции Z сверху.

3. Альтернативный оптимум
Если среди оценок свободных переменных в последней сим­плексной таблице есть хотя бы одна оценка, равная нулю, то задача имеет альтернативное решение, то есть хотя бы два оптимальных ре­шения. Для этих решений экстремальное значение функции будет одинаковое. Чем больше будет нулевых оценок, тем больше опти­мальных решений.

Пример 3:
Представим последнюю симплексную таблицу:

Таблица 2.5
Последняя симплексная таблица

Св.П Б.П.	Сj Ci	0	1	5
ai0	X1	X2
X3	1	6	3	(5)
X4	0	8	2	4
Z		6	2	0  ^

Х?опт (0,0,6,8)    Zmax = 6
Разрешающий столбец выбираем по нулевой оценке.

Таблица 2.6
Альтернативная симплексная таблица

Св.П Б.П.	Сj Ci	0	1	1
ai0	X1	X3
X2	5	6/5	3/5	1/5
X4	0	26/5	-2/5	-4/5
Z		6	2	0  ^

Х??опт (0,6/5,0,26/5)    Zmax = 6

4. Вырождение основной задачи линейного программирования
Если в опорном решении задачи хотя бы одна базисная перемен­ная принимает нулевое значение, то это решение называется вырож­денным, а задача линейного программирования, имеющая хотя бы одно вырожденное решение, — вырожденной задачей.

Вырождение наступает в тех случаях, когда при выборе разре­шающего элемента получается несколько одинаковых минимальных симплексных отношений. В этом случае в следующей симплексной таблице в столбце свободных членов появится хотя бы один нуль. Вырождение в больших задачах может привести к зацикливанию, то есть через некоторое число шагов мы можем прийти к опорному ре­шению, которое было уже получено раньше. Чтобы избежать зацик­ливания, разрешающий элемент нужно выбирать по определенному правилу, а именно: для тех строк разрешающего столбца, где получи­лись одинаковые минимальные симплексные отношения нужно со­ставить отношения элементов, стоящих в столбце за разрешающим столбцом, к элементам разрешающего столбца. Наименьшее отноше­ние с учетом знака даст разрешающую строку.

Пример 4:
Х1 + 2Х2 ? 4
2Х1 + Х2 ? 4
Х1 ? 2
Х2 ? 2
Хj ? 0, j = 1,2
Zmax = Х1+Х2.
Приводим к канонической форме
Х1 + 2Х2 + Х3 = 4
2Х1 + Х2 + Х4 = 4
Х1 + Х5 = 2
Х2 + Х6 = 2
Хj ? 0, j = 1,…,6
Zmax = Х1 + Х2 + 0*Х3 + 0*Х4 + 0*Х5 + 0*Х6.
Заполняем первую симплексную таблицу по алгоритму симплексного метода (табл. 2.7).

В оценочной строке две одинаковые отрицательные оценки, поэтому разрешающий столбец выбираем тот, который ближе к столбцу свободных членов. Минимальных симплексных отношений два, по­этому находим отношение элементов столбца Х2 к элементам столбца X1. После пересчета минимальное отношение находится в третьей строке и равно 0, следовательно, разрешающий элемент равен 1. Да­лее идет обычный пересчет.

Таблица 2.7
Первая симплексная таблица

Св.П Б.П.	Сj Ci	0	1	1	ai0/aip
ai0	X1	X2
X3	0	4	1	2	4 (2)
X4	0	4	2	1	2 (1/2)
X5	0	2	(1)	0	2 (0) <
X6	0	2	0	1	—
Z		0	-1 ^	-1