Как найти разность толщины два мм

Сумма и разность отрезков

Сумма

Суммой нескольких отрезков называют отрезок, составленный из длин данных отрезков.

Рассмотри два отрезка AB и CD:

Для нахождения их суммы можно расположить данные отрезки друг за другом на одной прямой, длина полученного отрезка и будет являться суммой данных отрезков:

Полученный отрезок, длина которого равна 12 см, и будет являться суммой данных отрезков, то есть:

AB + CD = 5 см + 7 см = 12 см.

Из данного примера можно сделать вывод, что для нахождения суммы отрезков надо сложить их длины.

Разность

Разностью двух отрезков называют отрезок, длина которого равна разности от вычитания длины меньшего отрезка из длины большего.

Рассмотри два отрезка AB и CD:

Для нахождения их разности можно взять больший отрезок, а затем от его начальной точки отложить длину меньшего отрезка. Длина отрезка, который лежит между конечными точками двух данных отрезков и будет их разностью:

Полученный отрезок, длина которого равна 7 см, и будет являться разностью данных отрезков, то есть:

CD — AB = 12 см — 5 см = 7 см.

Из данного примера можно сделать вывод, что для нахождения разности двух отрезков надо вычесть из длины большего отрезка длину меньшего.

Источник

Сравнение отрезков. Действия над отрезками.

Равные и неравные отрезки

Пусть нам даны два отрезка АВ и СD (рис.). Наложим отрезок АВ на отрезок CD так, чтобы точка А совпала с точкой С, и отрезок АВ направим по отрезку CD. Если точка В совпадаете точкой D, то отрезки АВ и CD равны; АВ = CD.

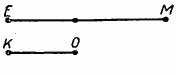
Сравним два отрезка КО и ЕМ (рис.).

Наложим отрезок КО на отрезок ЕМ так, чтобы точки К и Е совпали. Отрезок КО направим по отрезку ЕМ. Если точка О окажется где-нибудь между точками Е и М, то говорят, что отрезок ЕМ больше отрезка КО; отрезок КО меньше отрезка ЕМ.

Записывается это тaк: ЕМ > КО, КО 1 /₅ часть отрезка МN.

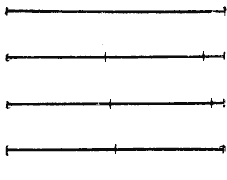
в) Чтобы разделить отрезок на равные части с помощью циркуля, поступают таким образом. Например, если нужно разделить отрезок на две равные части, то циркуль раздвигают на глаз так, чтобы раствор циркуля составлял примерно половину отрезка. Затем на данном отрезке от его конца последовательно один за другим откладывают этим раствором циркуля два отрезка. Если полученная сумма отрезков будет меньше данного отрезка, тo раствор циркуля увеличивают; если сумма окажется больше данного отрезка, то раствор циркуля уменьшают. Так, постепенно исправляя ошибку, можно отыскать довольно точнo половину отрезка (рис.).

Таким же образом выполняется приближённое деление отрезка на 3, 4, 5 и т. д. равных частей. Только в этом случае надо брать на глаз 1 /₃; 1 /₄; 1 /₅ . отрезка и откладывать взятый отрезок 3, 4, 5. раз, смотря по тому, на сколько равных частей надо разделить данный отрезок.

Свойство отрезков, отсекаемых параллельными прямыми на сторонах угла

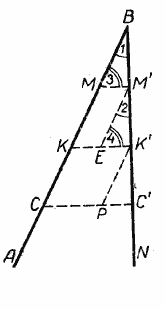
Пусть на стороне АВ угла АВN отложены равные отрезки ВМ = МК = КС (рис.) и через точки деления М, К и С проведены параллельные прямые, пересекающие сторону ВN того же угла.

На этой стороне образовались три отрезка: ВМ’, М’К’ и К’С’. Требуется доказать, что ВМ’ = М’К’ = К’С’.

Для доказательства через точки М’ и К’ проведём прямые, параллельные АВ. Мы получим треугольники ВММ’, М’ЕК’ и К’РС’. Сравним эти треугольники.

Сначала сравним треугольники МВМ’ и М’ЕК’. В этих треугольниках имеем:

∠1 = ∠2, как соответственные углы при параллельных ВА и М’Е и секущей ВN;

∠3 = ∠4, как острые углы 1 с соответственно параллельными сторонами (АВ || М’Е и ММ’ || КК’).

ВМ = МК по построению;

МК = М’Е, как противоположные стороны параллелограмма.

Углы 1-й и 4-й могут оказаться оба тупыми, но и в этом случае они останутся равными, а потому доказательство теоремы не изменится.

Следовательно, ВМ = М’Е. Таким образом, ΔВММ’ = ΔМ’ЕК’ (по стороне и двум прилежащим к ней углам). Отсюда следует, что ВМ’ = М’К’.

Так же можно доказать, что ВМ’ = К’С’, т. е. ВМ’ = М’К’ = К’С’. При доказательстве теоремы мы откладывание отрезков начали от вершины угла, но теорема справедлива и для того случая, когда откладывание отрезков будет начато не от вершины угла, а от любой точки его стороны.

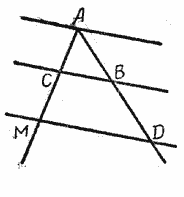
В этом случае вершину угла на чертеже можно не отмечать (рис.).

Теорема справедлива и для случая, когда прямые КО и МР параллельны.

Пропорциональные отрезки

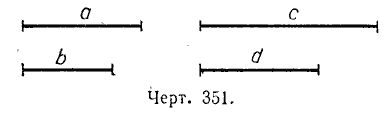
Из арифметики известно, что равенство двух отношений называется пропорцией. Например: 16 /₄ = 20 /₅; 2 /₃ = 4 /₆ To же самое имеем и в геометрии: если даны две пары отрезков, отношения которых равны, то можно составить пропорцию.

отрезки а, b, c, d называются пропорциональными.

Отношение a /_b называется, как и в арифметике, первым отношением, c /_d — вторым отношением; а и d называются крайними членами пропорции, b и с — средними членами.

В пропорции можно поменять местами отношения; можно переставить крайние члены, средние члены; можно переставить те и другие одновременно.

Поскольку в пропорции a /_b = c /_d под буквами подразумевают числа, выражающие длины отрезков, то произведение крайних членов её равно произведению средних членов. Отсюда, зная три члена пропорции, можно найти неизвестный четвёртый её член. Так, в пропорции a /_x = c /_d x = a • d /_c

Отметим ещё некоторые свойства пропорций, которыми придётся в дальнейшем пользоваться при доказательстве некоторых теорем и при решении задач.

а) Если три члена одной пропорции соответственно равны трём членам другой пропорции, то равны и четвёртые члены этих пропорций.

б) Если в пропорции равны предыдущие члены, то равны и последующие, т. е. если a /_x = a /_y , то х = у.

Чтобы убедиться в этом, переставим средние члены в этой пропорции.

А это возможно лишь в том случае, когда числитель и знаменатель дроби равны, т. е.

в) Если в пропорции равны последующие члены, то равны и предыдущие, т. е. если x /_a = y /_a , то х = у.

В справедливости этого свойства предлагается вам убедиться самостоятельно. Для этого проведите рассуждение, аналогичное предыдущему.

Построение пропорциональных отрезков

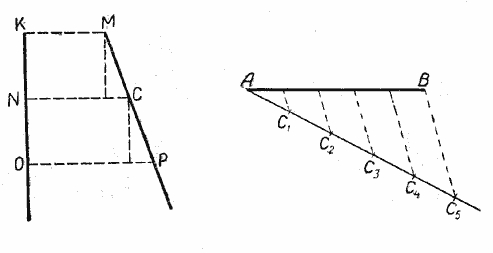
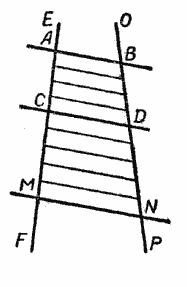
Пусть две прямые ЕF и ОР пересечены тремя параллельными прямыми АВ, СD и МN (рис.).

Требуется доказать, что отрезки АС, СМ, ВD и DN, заключённые между параллельными секущими, пропорциональны, т. е.

Пусть длина отрезка АС равна р, а длина отрезка СМ равна q.

Например, р = 4 см. и q = 5 см.

Разделим АС и СМ на отрезки, равные 1 см, и из точек деления проведём прямые, параллельные прямым АВ, СD и МN, как это показано на рисунке.

Тогда на прямой ОР отложатся равные между собой отрезки, при этом на отрезке BD их будет 4, а на отрезке DN — 5.

Отношение АС к СМ равно 4 /₅ , точно так же и отношение ВD к DN равно 4 /₅.

Значит, отрезки АС, СМ, ВD и DN пропорциональны. Пропорциональны также и отрезки АС, АМ, ВD и ВN (налегающие друг на друга), т. е. AC /_AM = BD /_BN,

Теорема будет справедлива и при любых других целых значениях р и q.

Если длины отрезков АС и СМ не выразятся в целых числах при данной единице измерения (например, сантиметре), то надо взять такую более мелкую единицу (например, миллиметр или микрон), при которой длины отрезков АС и СМ практически выразятся в целых числах.

Доказанная теорема справедлива и в том случае, когда одна из параллельных секущих проходит через точку пересечения данных прямых. Она справедлива также и в том случае, когда отрезки откладываются не непосредственно один за другим, а через некоторый промежуток.

Источник

2 класс — Математика 6. Сумма и разность длин отрезков

6. Сумма и разность длин отрезков

Прозвенел звонок и смолк –
Начинается урок.

Мы за парты тихо сели

И на доску посмотрели

2.Этап подготовки учащихся к активному сознательному усвоению знаний

Сегодня на уроке мы будем учиться складывать и вычитать длины отрезков. И узнаем что такое “сумма отрезков” и “разность отрезков”

Задание 1

Вставьте нужный знак

1см… 10мм 1cм =10мм

1дм …10см 1дм =10см

100cм… 1м 100см=1м

23мм … 32см 23мм 4дм

3м7дм …40дм 3м7дм 20мм 2см–это 20мм, значит 2см9мм>20мм

Задание 2

Назовите фигуры, изображенные на экране точка, отрезок, ломаная, треугольник, квадрат, четырёхугольник.

Что такое отрезок?

Отрезок – это часть прямой, у которой есть начало и конец.

Как обозначают начало и конец отрезка?

Начало и конец отрезка обозначают заглавными буквами латинского алфавита.

3.Этап усвоения новых знаний

Вспомните, при каком действии мы находим сумму?

Сумму находим сложением.

Какой знак при этом ставим?

Сложение обозначает знак (+)

При каком действии мы находим разность?

Разность находим при вычитании.

Какой знак при этом ставим?

Вычитание обозначает знак(-)

Начертите два отрезка длиной 3 см и 6 см.

Как найти сумму этих отрезков?

Измерить длину первого отрезка при помощи циркуля.

Отложить длину первого отрезка на луче, обозначив его начало и конец.

Измерить при помощи циркуля второй отрезок.

Отложить длину второго отрезка на луче от конца отрезка, полученный отрезок является суммой.

Запомните, конец одного отрезка является началом другого; суммой отрезков является отрезок.

Чтобы найти сумму длин двух отрезков, нужно сложить длины этих отрезков.

6 см + 3 см = 9 см

Как найти разность этих же отрезков?

Чтобы найти разность отрезков, необходимо:

Измерить длину первого отрезка при помощи циркуля

Отложить длину первого отрезка на луче, выделить его “дугой”.

Измерить длину второго отрезка при помощи циркуля.

Отложить длину второго отрезка на луче, выделить его “дугой” другого цвета.

Измерить длину оставшейся части отрезка – это будет разностью отрезков.

Запомните, что при вычитании отрезков оба отрезка нужно построить на луче от его начала.

Чтобы найти разность длин двух отрезков, нужно из длины большего отрезка вычесть длину меньшего отрезка.

6 см — 3 см = 3 см

4.Этап закрепления новых знаний

Задание 1

Сколько отрезков на этом рисунке?

Найдите длину самого большого отрезка. 4см+3см=7см

Задание 2

Начертите отрезок 9см. Отметьте на нём точку так, чтобы получился отрезок длиной 2см. Узнайте длину второго отрезка. 9cм-2cм=7cм

Задание 3

Начертите путь божьей коровки: вверх 2см, вправо 5см вниз 2 см, влево 5 см.

Какая фигура получилась?

Правильно, получился четырёхугольник. Как найти, сколько сантиметров проползла божья коровка?

Надо сложить длины всех сторон.

Задание

Нарисуйте такую же фигуру произвольных размеров. Узнайте, на сколько меньшая сторона в четырёхугольнике короче большей. Используйте при этом циркуль.

5.Этап подведения итогов

Что нового вы узнали о сумме и разности?

Мы узнали, что бывает сумма и разность длин отрезков.

Чем выражена разность отрезков?

Она выражена отрезком.

Чем выражена сумма отрезков?

Она выражена отрезком.

Чем отличается построение отрезков на луче при их сложении от построения отрезков при их вычитании?

При сложении конец первого отрезка является началом второго отрезка, а при вычитании – оба отрезка имеют общее начало.

Источник

Математика. 2 класс

Сумма и разность отрезков

Сумма и разность отрезков

Необходимо запомнить

Длины отрезков складываются и вычитаются, как обыкновенные числа.

Чтобы найти сумму длин двух отрезков, нужно сложить длины этих отрезков.

Чтобы найти разность длин двух отрезков, нужно из длины большего отрезка вычесть длину меньшего отрезка.

Интересные факты

Люди давно приметили, что число семь – непростое число, даже, можно сказать, волшебное. Прислушайтесь: именно семь дней творения мира, семь дней в неделе, семь, а не восемь, цветов радуги, семь нот на нотном стане.

В народных и авторских сказках очень часто встречается число семь. Например, в сказках «Волк и семеро козлят», «Сказка о мёртвой царевне и семи богатырях», «Белоснежка и семь гномов», «Храбрый портняжка», «Цветик – семицветик». В устном народном творчестве ни с одним числом нет столько пословиц и поговорок. Приведём примеры: «Семеро одного не ждут», «Семь раз отмерь, один отрежь», «У семи нянек дитя без глаза (без присмотра)», «Семь пядей во лбу» (талантливый), «Семь пятниц на неделе» (о человеке, который часто меняет свои решения), «До седьмого пота» (работать до утомления).

НАШИ ПАРТНЁРЫ

© Государственная образовательная платформа «Российская электронная школа»

Источник

Что значит разность длин

6. Сумма и разность длин отрезков

1. Организационный этап

Прозвенел звонок и смолк –
Начинается урок.
Мы за парты тихо сели
И на доску посмотрели

2. Этап подготовки учащихся к активному сознательному усвоению знаний

1. Целеполагание

Сегодня на уроке мы будем учиться складывать и вычитать длины отрезков. И узнаем что такое “сумма отрезков” и “разность отрезков”

2. Устный счёт

Задание 1

Вставьте нужный знак

1 см… 10 мм 1 cм =10 мм

1 дм …10 см 1 дм =10 см

100 cм… 1 м 100 см=1 м

23 мм … 32 см 23 мм 4 дм

3 м 7 дм …40 дм 3 м 7 дм 20мм 2 см – это 20 мм, значит 2 см 9 мм>20 мм

Задание 2

Назовите фигуры, изображенные на экране (точка, отрезок, ломаная, треугольник, квадрат, четырёхугольник)

Что такое отрезок?

Отрезок – это часть прямой, у которой есть начало и конец.

Как обозначают начало и конец отрезка?

Начало и конец отрезка обозначают заглавными буквами латинского алфавита.

3. Этап усвоения новых знаний

Вспомните, при каком действии мы находим сумму?

Сумму находим сложением.

Какой знак при этом ставим?

Сложение обозначает знак (+)

При каком действии мы находим разность?

Разность находим при вычитании.

Какой знак при этом ставим?

Вычитание обозначает знак (-)

Начертите два отрезка длиной 3 см и 6 см.

Как найти сумму этих отрезков?

Измерить длину первого отрезка при помощи циркуля.

Отложить длину первого отрезка на луче, обозначив его начало и конец.

Измерить при помощи циркуля второй отрезок.

Отложить длину второго отрезка на луче от конца отрезка, полученный отрезок является суммой.

Запомните, конец одного отрезка является началом другого; суммой отрезков является отрезок.

Чтобы найти сумму длин двух отрезков, нужно сложить длины этих отрезков.

Как найти разность этих же отрезков?

Чтобы найти разность отрезков, необходимо:

Измерить длину первого отрезка при помощи циркуля

Отложить длину первого отрезка на луче, выделить его “дугой”.

Измерить длину второго отрезка при помощи циркуля.

Отложить длину второго отрезка на луче, выделить его “дугой” другого цвета.

Измерить длину оставшейся части отрезка – это будет разностью отрезков.

Запомните, что при вычитании отрезков оба отрезка нужно построить на луче от его начала.

Чтобы найти разность длин двух отрезков, нужно из длины большего отрезка вычесть длину меньшего отрезка.

4. Этап закрепления новых знаний

Задание 1

Сколько отрезков на этом рисунке?

Найдите длину самого большого отрезка. 4 см+3 см=7 см

Задание 2

Начертите отрезок 9 см. Отметьте на нём точку так, чтобы получился отрезок длиной 2 см. Узнайте длину второго отрезка. 9 cм-2 cм=7 cм

Задание 3

Начертите путь божьей коровки: вверх 2 см, вправо 5 см. вниз 2 см, влево 5 см.

Какая фигура получилась?

Правильно, получился четырёхугольник. Как найти, сколько сантиметров проползла божья коровка?

Надо сложить длины всех сторон.

2 см+5 см+2 м+5 см=14 см

Логические задания

Задание

Нарисуйте такую же фигуру произвольных размеров. Узнайте, на сколько меньшая сторона в четырёхугольнике короче большей. Используйте при этом циркуль.

5. Этап подведения итогов

Что нового вы узнали о сумме и разности?

Мы узнали, что бывает сумма и разность длин отрезков.

Чем выражена разность отрезков?

Она выражена отрезком.

Чем выражена сумма отрезков?

Она выражена отрезком.

Чем отличается построение отрезков на луче при их сложении от построения отрезков при их вычитании?

При сложении конец первого отрезка является началом второго отрезка, а при вычитании – оба отрезка имеют общее начало.

Рефлексия

сегодня я узнал

Спасибо за урок!

Остались вопросы по теме? Наши репетиторы готовы помочь!

Подготовиться к ЕГЭ, ОГЭ и другим экзаменам

Подготовиться к поступлению в любой ВУЗ страны

Источник

Разностью принято называть результат, полученный путем вычитания меньшего числа из большего. В данном случае, первое число из которого вычитается другое, получает название уменьшаемое (ведь именно его мы уменьшаем в процессе). Второе же, вычитаемое из первого числа, так и называется вычитаемым. В сумме с разностью вычитаемое составляет собой уменьшаемое, а разница между уменьшаемым и разностью становится вычитаемым. В случаях, когда вычитаемое превышает собой уменьшаемое, разность чисел становится отрицательной.

Существует несколько формул разности:

1. формула разности a-b = с
2. формула разности квадратов a 2 — b 2 = (a — b)*(a + b)
3. формула разности кубов a 3 — b 3 = (a — b)*(a 2 + ab + b 2)
4. формула разности потенциалов U=Aq
5. формула квадрата разности (a — b) 2 = a 2 — 2ab + b 2
6. формула куба разности (a — b) 3 = a 3 — 3a2b + 3ab 2 — b 3

Что такое разность и как ее найти

Вычислить разность можно с помощью обычного, привычного нам калькулятора. Для этого, следует нажать кнопку «С», ввести числа уменьшаемого, после чего нажать кнопку «-» и вводить вычитаемое. Результат получаем с помощью нажатия кнопки «=». Существуют и менее распространенные модели калькуляторов с обратной, так называемой польской записью. Здесь, для вычисления разности, вместо кнопки «-» следует нажать кнопку с изображением стрелки вверх (благодаря этому, число переходит в стек или карту памяти действия). После этого, вводим вычитаемое и нажимаем кнопку «-», получая готовый ответ.

Существует также и некий суммирующий прибор, в возможности которого входит исключительно сложение чисел. Есть возможность найти разность и с помощью его. Для этого, необходимо мысленно уменьшить вычитаемое на 1. После этого, переводим цифры числа в разряд дополнительных, где 0 равен 9, 1 равен 8 и т.д. Старшие разряды, оставшиеся свободными, заполняем девятками. Сложенные составляющие разности такого рода заставляет счетчик прибора переполниться и индицировать разность.

Что такое разность потенциалов

Понятие разности потенциалов используется физиками. Получить разность потенциалов можно, подключив вольтметр к двум точкам цепи, где напряжение первой условно равно U1, а второй — U2. В таком случае вольтметр покажет результат в виде напряжения U1-U2, что и называется разностью потенциалов. Любой гальванический элемент вырабатывает напряжение, которое определяет разность электрохимических потенциалов, составляющих электроды элемента веществ.

До того, как были изобретены стабилизаторы напряжения, осуществить калибровку вольтметров позволяли элементы Вестона. Подобранные в них реагирующие составляющие обеспечивали высокий уровень стабильности разности потенциалов. Также существует понятие разности давлений, использующееся в гидравлическом и пневматическом оружии. Такая разность представляет собой аналог разности электротехнических потенциалов.

Как научить ребенка вычитанию и сложению

Еще до начала школы ребенку желательно освоить элементарные математические действия, получить понятие о том, что такое разность или сумма. Для того, чтобы малышу было проще считать, используйте в процессе обучения любые подручные средства. Не бойтесь визуализировать задачу. К примеру, малышу будет куда проще решить, сколько яблок у него останется, если он поделится половиной с другом на реальных предметах, а не на безликом листе бумаги.

Очень нравятся детям и задачи связанные с угадыванием. К примеру. стандартный пример «2+2=4» можно заменить на «2+х=4». Такое упражнение заставит ребенка мыслить не по шаблону и разовьет логику.

В начальной школе ребенок впервые знакомится с математикой, и его первыми примерами являются такие простые действия, как складывание или вычитание. Но иногда ребенку сложно объяснить даже такие, казалось бы, несложные и привычные взрослым примеры. Как же научиться находить сумму и разность чисел?

Что такое сумма, и как ее найти

Сумма – это результат складывания двух чисел (слагаемых), между которыми стоит знак +. Чтобы получить сумму, нужно к одному слагаемому прибавить второе слагаемое. В общем виде пример можно показать так: a + b = s, где а – первое слагаемое, b – второе слагаемое, а s – результат сложения этих двух слагаемых. При этом нужно знать, что от перестановки слагаемых сумма не меняется, — это одно из самых первых правил в математике, которое проходят в начальной школе.

Чтобы наглядно показать ребенку, как сложить числа, возьмите конфеты или любые другие вещи. Покажите ребенку две конфеты, а затем прибавьте к этим конфетам еще две. Пусть ребенок посчитает и скажет, что теперь конфет оказалось четыре. Объясните ему, что он только что сложил эти числа, то есть прибавил к одному числу другое число и в конечном итоге получил сумму.

Немного сложнее объяснить сложение разрядных слагаемых , эта тема может быть непонятна ребенку. Итак, существует множество разрядов: единицы, десятки, тысячи. Возьмите, к примеру, число 2564. Если разложить его на разряды, то получится: 2564 = 2000 + 500 + 60 + 4. Чтобы прибавить к этому числу, например, число 305, воспользуйтесь сложением в столбик. При таком сложении нужно прибавлять одни разряды к другим, начиная с конца: единицы к единицам, десятки к десяткам, тысячи к тысячам. То есть, для начала складываем 4 и 5, затем 6 и 0, после 5 и 3, и в конце 2 и 0. В конечном итоге получаем число 2869.

Как найти разность чисел

Разность – результат вычитания одного числа из другого. В отличие от суммы, здесь мы не можем воспользоваться правилом «от перестановки слагаемых разность не меняется», так как в вычитании всегда есть уменьшаемое и вычитаемое. Чтобы найти вычитаемое и разность , для начала нужно разобраться с этими понятиями. Уменьшаемое – это то, из чего мы «вычитаем», то есть убираем, а вычитаемое – количество того, что мы у этого уменьшаемого вернем.

В общем виде вычитание можно записать так: a — b = r.
Обратимся к тем же конфетам, с которыми мы разбирали сумму чисел. Чтобы помочь ребенку найти разность чисел , возьмите пять конфет. Пусть ребенок посчитает и убедится, что их пять. Затем заберите себе три конфеты. Ребенок скажет, что их осталось две. А сколько тогда забрали? Три.

А что касается разрядных слагаемых, то здесь мы делаем то же самое, что и с суммой, только теперь не прибавляем, а вычитаем. Возьмем число 6845 и вычтем из него 4231. Для этого мы вычитаем один разряд из другого разряда, производя вычитание с конца: 5-1 = 4, 4-3 = 1, 8-2 = 6, 6-4 = 2. В ответе получим 2614.

Для многих точные науки, вроде математики, воспринимаются как нечто более простое, чем сферы, требующие рассуждений, предполагающие большую вариативность. Однако все предметы имеют свои сложности, в том числе и технические.

Вычитание

Для того, чтобы понять, чем является разность, необходимо разобраться в ряде математической терминологии. В первую очередь, нужно выяснить, чем является вычитание.

По-другому это понятие называют убавлением, и по такому названию понять смысл процесса несколько проще. По своей сути вычитание является одной из математических операций. Что же это за операции? Как правило, под ними понимают определенные арифметические или логические действия. Встает логичный вопрос – в чем же суть арифметических действий?

Понятие арифметики появилось достаточно давно. Оно зародилось в древнегреческом языке, где переводилось как «число». Сегодня это раздел математики, который изучает числа, их отношения друг к другу, а также свойства.

Итак, вычитание – это операции с числами, относящиеся к бинарным
. Суть бинарных операций в том, что в них используются два аргумента (параметра), и получается один результат.

Стоит рассмотреть, как найти разность какого-то числа. В первую очередь, необходимы два аргумента, то есть два числа. Затем необходимо уменьшить значение первого числа на значение второго. Когда данная операция выражается письменно, используется знак «минус». Это выглядит так: а – б = с, где а является первым числовым значением, б – вторым, а с – разностью чисел.

Свойства и особенности

Как правило, у учеников возникает гораздо больше проблем именно с вычитанием, нежели со сложением. Отчасти это связано со свойствами данных математических операций. Всем известно, что от перемены мест слагаемых значение суммы не меняется. В вычитании же всё гораздо сложней. Если поменять числа местами, получится совершенно другой результат. Схожим свойством в прибавлении и убавлении является то, что нулевой элемент не меняет исходное число.

В вычитании всё относительно просто, если первое число больше второго, однако в школе будут рассматриваться и противоположные примеры. В этом случае возникает понятие отрицательного числа.

Например, если нужно вычесть из 5 число 2, то всё несложно. 5-2=3, таким образом разность числа составит 3. Однако, что делать, если необходимо посчитать, сколько будет два минус пять?

В выражении 2-5 разность уйдет в минус, то есть в отрицательное значение. Из двойки легко можно вычесть двойку, получив таким образом ноль, однако от пятерки остается ещё три. Таким образом, результатом данного выражения будет отрицательное число три. То есть, 2-5=-3.

Особенности вычитания отрицательных чисел

Также бывают ситуации, когда второе число, по сути, меньше первого, однако является отрицательным. Например, рассмотрим выражение 7-(-4). Проще всего разобраться с этой операцией путем превращения комбинации –(- в обычный плюс. Знаки даже внешне напоминают его. В связи с этим, результатом выражения, то есть разницей чисел, будет 11.

Если оба числа являются отрицательными, то вычитание будет происходить следующим образом.

6-(-7): минус у первого числа сохранится, а комбинация из двух последующих минусов превратится в плюс. Таким образом, необходимо понять, сколько будет -6+7. Разницу найти нетрудно – она равняется единице.

Если же необходимо вычесть положительное число из отрицательного, то выражение можно представить как простое сложение, а затем подписать к результату минус. Например, -3-4 (4 – положительное число), в результате даст -7.

Слово «разность» может употребляться во многих значениях. Это может означать и разницу чего-либо, например, мнений, взглядов, интересов. В некоторых научных, медицинских и других профессиональных сферах этим термином обозначают разные показатели, к примеру, уровня сахара в крови, атмосферного давления, погодных условий. Понятие «разность», как математический термин тоже существует.

Вконтакте

Арифметические действия с числами

Основными арифметическими действиями в математике являются:

• сложение;
• вычитание;
• умножение;
• деление.

Каждый результат этих действий также имеет своё название:

• сумма — результат, получившийся при сложении чисел;
• разность — результат, получившийся при вычитании чисел;
• произведение — результат умножения чисел;
• частное — результат деления.

Более простым языком объясняя понятия суммы, разности, произведения и частного в математике, можно упрощённо записать их лишь как словосочетания:

• сумма — прибавить;
• разность — отнять;
• произведение — умножить;
• частное — разделить.

Рассматривая определения
, что же такое разность чисел в математике, можно обозначить это понятие несколькими способами:

И все эти определения являются верными
.

Как найти разницу величин

Возьмём за основу то обозначение разности, которое нам предлагает школьная программа:

• Разностью называется результат вычитания одного числа из другого. Первое из этих чисел, из которого осуществляется вычитание, называется уменьшаемым, а второе, которое вычитают из первого, называется вычитаемым.
  

Ещё раз прибегнув к школьной программе, мы находим правило, как найти разность:

• Чтобы найти разность, надо от уменьшаемого отнять вычитаемое.
  

Всё понятно. Но при этом мы получили ещё несколько математических терминов. Что они значат?

• Уменьшаемое — это математическое число, от которого отнимают и оно уменьшается (становится меньше).
  
• Вычитаемое — это математическое число, которое вычитают из уменьшаемого.
  

Теперь понятно, что разность состоит из двух чисел, которые для её вычисления должны быть известны. А как их найти тоже воспользуемся определениями:

• Чтобы найти уменьшаемое, надо к вычитаемому прибавить разность.
  
• Чтобы найти вычитаемое, нужно из уменьшаемого вычесть разность
  .

Математические действия с разностью чисел

Опираясь на выведенные правила, можно рассмотреть наглядные примеры. Математика, интереснейшая наука. Мы здесь возьмём для решения лишь самые простые цифры. Научившись вычитать их, вы научитесь решать и более сложные значения, трёхзначные, четырёхзначные, целые, дробные, в степенях, корнях, другие.

Простые примеры

• Пример 1. Найти разницу двух величин.

20 — уменьшаемое значение,

15 — вычитаемое.

Решение: 20 — 15 = 5

Ответ: 5 — разница величин.

• Пример 2. Найти уменьшаемое.

48 — разность,

32 — вычитаемое значение.

Решение: 32 + 48 = 80

• Пример 3. Найти вычитаемое значение.

7 — разность,

17 — уменьшаемая величина.

Решение: 17 — 7 = 10

Ответ: вычитаемое значение 10.

Более сложные примеры

На примерах 1-3 рассмотрены действия с простыми целыми числами. Но в математике разницу вычисляют с применением не только двух, но и нескольких чисел, а также целых, дробных, рациональных, иррациональных, др.

• Пример 4. Найти разницу трёх значений.

Даны целые значения: 56, 12, 4.

56 — уменьшаемое значение,

12 и 4 — вычитаемые значения.

Решение можно выполнить двумя способами
.

1 способ (последовательное отнимание вычитаемых значений):

1) 56 — 12 = 44 (здесь 44 — получившаяся разница двух первых величин, которая во втором действии будет уменьшаемым);

2 способ (отнимание из уменьшаемого суммы двух вычитаемых, которые в таком случае называются слагаемыми):

1) 12 + 4 = 16 (где 16 — сумма двух слагаемых, которая в следующем действии будет вычитаемым);

2) 56 — 16 = 40.

Ответ: 40 — разница трёх значений.

• Пример 5. Найти разницу рациональных дробных чисел.

Даны дроби с одинаковыми знаменателями, где

4/5 — уменьшаемая дробь,

3/5 — вычитаемая.

Чтобы выполнить решение, нужно повторить действия с дробями. То есть, надо знать как отнимать дроби с одинаковым знаменателем. Как обращаться с дробями, имеющими разные знаменатели. Их надо уметь привести к общему знаменателю.

Решение: 4/5 — 3/5 = (4 — 3)/5 = 1/5

Ответ: 1/5.

• Пример 6. Утроить разницу чисел.

А как выполнить такой пример, когда требуется удвоить или утроить разницу?

Вновь прибегнем к правилам:

• Удвоенное число — это величина, умноженная на два.
  
• Утроенное число — это величина, умноженная на три.
  
• Удвоенная разность — это разница величин, умноженная на два.
  
• Утроенная разность — это разница величин, умноженная на три.
  

7 — уменьшаемая величина,

5 — вычитаемая величина.

2) 2 * 3 = 6. Ответ: 6 — разница чисел 7 и 5.

• Пример 7. Найти разницу величин 7 и 18.

7 — уменьшаемая величина;

18 — вычитаемая.

Вроде всё понятно. Стоп! Вычитаемое больше уменьшаемого?

И опять есть применяемое для конкретного случая правило:

• Если вычитаемое больше уменьшаемого, разница окажется отрицательной.
  

Ответ: — 11. Это отрицательное значение и есть разница двух величин, при условии, что вычитаемая величина больше уменьшаемой.

Математика для блондинок

Во Всемирной паутине можно найти массу тематических сайтов, которые ответят на любой вопрос. Точно так же в любых математических расчётах вам помогут онлайн-калькуляторы на любой вкус. Все расчёты, производимые на них, прекрасное подспорье для торопливых, нелюбознательных, ленивых. Математика для блондинок — один из таких ресурсов. Причём прибегаем к нему мы все, независимо от цвета волос, пола и возраста.

В школе подобные действия с математическими величинами нас учили вычислять в столбик, а позднее — на калькуляторе. Калькулятор — это также удобное подспорье. Но, для развития мышления, интеллекта, кругозора и других жизненных качеств, советуем производить арифметические действия на бумаге или даже в уме. Красота человеческого тела — это великое достижение современного фитнес-плана. Но мозг — это тоже мышца, которая требует иногда её качать. А значит, не откладывая, начинайте думать.

И пусть в начале пути вычисления сводятся к примитивным примерам, всё у вас впереди. А освоить придётся немало. Мы видим, что действий с разными величинами в математике множество. Поэтому кроме разницы необходимо изучить, как вычислить и остальные результаты арифметических действий:

• сумму — сложением слагаемых;
• произведение — умножением множителей;
• частное — делением делимого на делитель.

Вот такая интересная арифметика.

Разность или вычитание целых чисел напрямую связана с темой сложение целых чисел. Ведь зная сумму и одно из слагаемых, можно найти второе слагаемое. Рассмотрим пример:

У нас есть 10 яблок в корзине. В первый раз в корзину добавили 2 яблока, сколько во-второй раз добавили яблок в корзину, чтобы в итоге получить 10 яблок?
Обозначим за переменную x – количество яблок, добавленных во второй раз. Если мы прибавим к переменной x два яблока, то получим 10 яблок. Математически запись будет выглядеть так:

чтобы найти переменную x нужно из корзины убрать 2 яблока или от суммы 10 отнять одно известное слагаемое 2.

То есть переменная x=8.

Определение:

Разностью двух целых чисел называется целое число, которое в сумме с вычитаемым дает уменьшаемое.

Разность целых чисел a и b обозначается как a-b.

Разность
a-
b это сумма чисел
a и противоположного числа
b.

a-
b=
a+(-
b)

где b и –b – это противоположные числа.

Пример:

5-2=5+(-2)=3

Вычитание целых положительных чисел в примерах.

Пример:

Выполните вычитание из целого числа 12 число 5.

Решение:
По правилу разности мы должны заменить вычитаемое 5 заменить на противоположное число, то есть -5 и выполнить .

Пример:

Из числа 37 выполните вычитание числа 56.

Решение:
Нужно вычитаемое число 56 заменить на противоположное число, то есть число -56 и выполнить сложение целых чисел с разными знаками.

37-56=37+(-56)=-21

Пример:

Из числа -4 нужно вычесть число 7.

Решение:
Заменяем вычитаемое число 7 на противоположное число -7 и складываем из по правилу

4-7=-4+(-7)=-11

Вычитание целых отрицательных чисел в примерах.

Пример:

Найдите разность чисел 6 и -8.

Решение:
По правилу разности нужно заменить вычитаемое -8 на противоположное число +8 или 8 и посчитать сумму целых чисел. Получим:

Из целого числа -14 вычтите число -10.
Нужно вычитаемое -10 заменить на противоположное число +10 или 10 по правилу вычитания целых чисел и потом выполнить сложение.

14-(-10)=-14+10=-4

Вычитание нуля из целых чисел.

Если вычесть нуль из целого числа, то число не измениться
.

Рассмотрим пример:

3-0=3+0=3

a-0=
a

Если вычесть нуль из нуля, то получим нуль.

Вычитание одинаковых целых чисел.

Рассмотрим задачу:

Миша получил от мамы 2 конфеты и он тут же угостил своего друга Сашу двумя конфетами. Сколько осталось конфет у Миши?

Решение:
Миша получил 2 конфеты и отдал 2 конфеты, математически можно записать так:

Ответ: у Миши осталось 0 конфет.

То есть если выполнить вычитание равных чисел в результате получим нуль.

Проверка результата вычитания.

Как проверить правильно ли вы нашли разность двух целых чисел?
Ответ прост он заключается в самом определении разности двух целых чисел. Нужно разность сложить с вычитаемым получим уменьшаемое
. Словесная формула будет выглядеть так:

Разность+Вычитаемое=Уменьшаемое

Пример:

19-5=14

19 – это у нас уменьшаемое;
5 – вычитаемое;
14 – разность.

Выполним проверку:
К разности прибавим уменьшаемое, если правильно выполнили вычитание, то получим уменьшаемое.

Еще пример:

Выполните проверку вычитания 12-23=-11

12 – уменьшаемое;
23 – вычитаемое;
-11 – разность.

Выполним проверку вычитания:
Разность+Вычитаемое=Уменьшаемое

Разность — толщина

Cтраница 1

Разность толщин до прокатки и после прокатки В — В называется абсолютным обжатием.
 [1]

Разность толщины Н — h называется величиной абсолютного сжатия.
 [2]

Разность толщины рабочих ( установочных) колодок не должна превышать 0 02 мм.
 [3]

Разность толщины заготовки до и после прокатки Н — h называется величиной абсолютного обжатия. Участок abed, на котором происходит обжатие металла при прокатке, называется зоной деформации. Дуга ab, по которой валок соприкасается с металлом, называется дугой захвата, а центральный угол а, соответствующий этой дуге, углом захвата.
 [4]

Разность толщины заготовки до и после прокатки Huh ( рис. IV-10 a) называют величиной абсолютного обжатия. Участок а, Ь, с, d, на котором происходит обжатие металла при прокатке, называют зоной деформации. Дугу а — Ъ или с — d, по которой валок соприкасается с металлом, называют дутой захвата, а центральный угол а, соответствующий этой дуге, углом захвата.
 [5]

Разность толщины прокладок должна быть 3 535 мм.
 [6]

Разность толщин стыкуемых труб не должна превышать 15 % от толщины стенки трубы.
 [8]

Разность толщины стыкуемых труб не должна превышать 15 % толщины стенки трубы.
 [9]

Разность толщин стыкуемых труб из углеродистых сталей должна быть не более 15 % от средней толщины стенки. При сварке труб из аустенитной стали особенно важно совпадение внутренних диаметров.
 [10]

Разность толщины спинки обода блока, измеренная на участке внешних необработанных поверхностей на разных радиусах, должна быть не более 10 % от ее толщины.
 [11]

Разность толщины спинки обода блока, измеренная на участке внешних необработанных поверхностей на разных радиусах, должна быть не более 10 % от ее толщины.
 [12]

Разность толщины спинки обода блока, измеренная на участке внешних необработанных поверхностей на равных радиусах, должна быть не более 10 % от ее толщины.
 [13]

Если разность толщин большая, чем указано выше, на листе, имеющем большую толщину, должен быть сделан скос длиной 5 ( 5 ] — 5) — при одностороннем превышении кромки и длиной 2 5 ( Si-5) — при двустороннем превышении кромок до толщины тонкого листа.
 [14]

Если разность толщин свариваемых встык листов превышает указанную, то на листе, имеющем большую толщину Si, должен быть сделан скос кромок до толщины S тонкого листа.
 [15]

Страницы:  

   1

   2

   3

   4

Толщину каждой
планки измеряйте в девяти точках,
равномерно распределенных по площади
планки. Наибольшая разность полученных
значений толщины каждой планки не должна
быть более 0,003 мм.

Вычислите среднее
арифметическое значение результатов
измерения толщины каждой планки.
Определите разность средних значений
толщины планок в следующих сочетаниях:1—2,
2一3，
1—3.
Наибольшая из полученных разностей не
должна превышать 0,005 мм.

2.3.24. Определение несовпадения линии центров с рабочими плоскостями измерительных ножей, располагаемых на опорных поверхностях каретки продольного перемещения.

На каждую опорную
поверхность поместите приблизительно
в среднем сечении по блоку концевых мер
длины. Длина каждого блока

l=А+В+

где
А ——номинальная
высота измерительного ножа (5 мм);

В
——среднее арифметическое
значение толщины планок для установки
измерительных ножей, мм;

Д——диаметр
цилиндрического валика длиной 200 мм.

Установите
цилиндрический валик в центра. Закрепите
измерительную головку со сферическим
наконечником в кронштейне К₁
на объективе
визирной системы.

Приведите наконечник
измерительной головки в контакт с
измерительной поверхностью одного из
блоков концевых мер и снимите первое
показание
(а₁)
по шкале измерительной головки. Затем,
передвигая каретку поперечного
перемещения, приведите наконечник в
контакт с наивысшей точкой поперечного
сечения валика и снимите второе показание
а₂.

Разверните
кронштейн с измерительной головкой
так, чтобы можно было привести измерительный
наконечник в контакт с измерительной
поверхностью блока концевых мер,
находящегося на противоположной опорной
поверхности. Передвигайте каретку
поперечного перемещения до получения
контакта наконечника с наивысшей точкой
образующей валика в том же среднем
сечении. Соответственно получите отсчеты
а₃
и а₄.
По максимальному значению двух
сравниваемых разностей а₂
—
а₁
и
а₄
—
а₃
оценивают
несовпадение линии центров с рабочей
плоскостью измерительных ножей, которое
не должно
превышать ±0,01 мм. При этом разности не
должны расходиться между собой более
чем на 0,01 мм.

Проверку несовпадения
линии центров с плоскостью измерительных
ножей производите в среднем и двух
крайних сечениях валика, перекладывая
соответственно блоки концевых мер на
опорных поверхностях продольной каретки.

Примечание.
До начала измерения, вращая валик в
центрах на 360°, установите его в положение
наибольшего или наименьшего биения.

2.3.25. Определение отклонения от параллельности линии обратных центров направлению движения каретки продольного перемещения.

Отклонение
определяйте в вертикальной и горизонтальной
плоскостях, установив в скалках обратные
центра и закрепив в них цилиндрический
валик с прямыми,центрами.

Методика проверки
аналогична указанной в подразделе
2.3.22.

Разность показаний
по шкале измерительной головки не должна
превышать при поверке в вертикальной
плоскости 0,010 мм на расстоянии 100 мм, при
поверке в горизонтальной плоскости
0,030 мм на расстоянии 100 мм.

Предметный
стол

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

1 ответ:

Читайте также