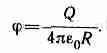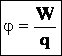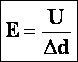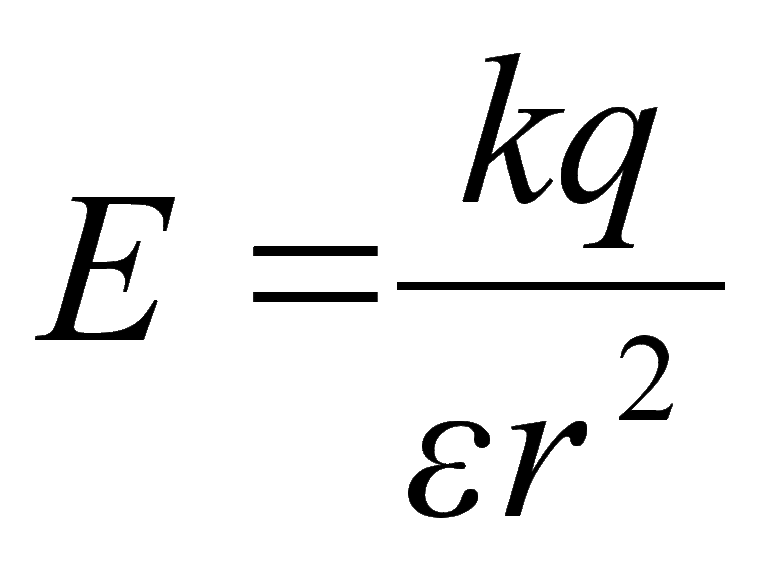Установленная в
§ 85 связь между напряженностью поля
и потенциалом позволяет по известной
напряженности поля найти разность
потенциалов между двумя произвольными
точками этого поля.
1.
Поле равномерно заряженной бесконечной
плоскости определяется
формулой (82.1): E=/(20),
где
— поверхностная плотность заряда.
Разность потенциалов между точками,
лежащими на расстояниях х1,
и
x2
от
плоскости
140
(используем формулу
(85.1)), равна
2.
Поле двух бесконечных параллельных
разноименно заряженных плоскостей
определяется
формулой (82.2): Е=/0,
где
—
поверхностная плотность заряда.
Разность потенциалов между плоскостями,
расстояние между которыми равно
d
(см. формулу (85.1)), равна
3.
Поле равномерно заряженной сферической
поверхности радиуса
R
с
общим
зарядом Q
вне
сферы
(r>R)
вычисляется
по (82.3):
E=(1/40)Q/r2.
Разность потенциалов между двумя
точками, лежащими на расстояниях r1
и r2
от
центра сферы (r1>R,
r2>R),
равна
Если
принять r1=r
и r2=,
то потенциал поля вне сферической
поверхности, согласно формуле (86.2),
задается выражением
(ср. с формулой
(84.5)). Внутри сферической поверхности
потенциал всюду одинаков и равен
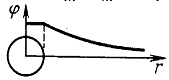
График
зависимости
от r
приведен
на рис. 134.
4.
Поле объемно заряженного шара радиуса
R
с
общим зарядом Q
вне
шара
(r>R)
вычисляется
по формуле (82.3), поэтому разность
потенциалов между двумя точками,
лежащими на расстояниях r1
и
r2
от центра шара (r1>R,
r2>R),
определяется
формулой (86.2). В любой точке, лежащей
внутри
шара
на расстоянии r‘
от
его центра (r'<R),
напряженность
определяется выражением (82.4):
E=(1/40)(Q/R3)r’.
Следовательно,
разность потенциалов между двумя
точками, лежащими на расстояниях r‘1
и
r‘2
от
центра шара (r’1<R,
r’2<R),
равна
5.
Поле равномерно заряженного бесконечного
цилиндра радиуса
К,
заряженного
с линейной плотностью т, вне цилиндра
(r>R)
определяется формулой (82.5):
E=(1/20)(/r).
Следовательно, разность потенциалов
между двумя точками, лежащими на
расстояниях r1
и
r2
от
оси заряженного цилиндра (r1>R,
r2>R),
равна
§ 87. Типы диэлектриков. Поляризация диэлектриков
Диэлектрик
(как и всякое вещество) состоит из
атомов и молекул. Так как положительный
заряд всех ядер молекулы равен
суммарному заряду электронов, то молекула
в целом электрически нейтральна.
Если заменить положительные заряды
ядер молекул суммарным зарядом +Q,
находящемся
в центре «тяжести» положительных
зарядов, а заряд всех электронов —
суммарным отрицательным зарядом —Q,
находящемся
в центре «тяжести» отрицательных
зарядов, то молекулу можно рассматривать
как электрический диполь с электрическим
моментом, определенным формулой (80.3).
Первую
группу диэлектриков (N2,
H2,
О2,
СO2,
СH4,
…) составляют вещества,
141
молекулы
которых имеют симметричное строение,
т. е. центры «тяжести» положительных
и отрицательных зарядов в отсутствие
внешнего электрического поля совпадают
и, следовательно, дипольный момент
молекулы р
равен нулю. Молекулы
таких
диэлектриков называются неполярными.
Под
действием внешнего электрического
поля заряды неполярных молекул смещаются
в противоположные стороны (положительные
по полю, отрицательные против поля) и
молекула приобретает дипольный
момент.
Вторую
группу диэлектриков (H2O,
NH3,
SO2,
CO, …)
составляют вещества, молекулы которых
имеют асимметричное строение, т. е.
центры «тяжести» положительных и
отрицательных зарядов не совпадают.
Таким образом, эти молекулы в отсутствие
внешнего электрического поля обладают
дипольным моментом. Молекулы
таких
диэлектриков называются полярными.
При
отсутствии внешнего поля, однако,
дипольные моменты полярных молекул
вследствие теплового движения
ориентированы в пространстве хаотично
и их результирующий момент равен нулю.
Если такой диэлектрик поместить во
внешнее поле, то силы этого поля будут
стремиться повернуть диполи вдоль поля
и возникает отличный от нуля результирующий
момент.
Третью
группу диэлектриков (NaCl,
КСl,
КВг,…) составляют вещества, молекулы
которых имеют ионное строение. Ионные
кристаллы представляют собой
пространственные решетки с правильным
чередованием ионов разных знаков. В
этих кристаллах нельзя выделить отдельные
молекулы, а рассматривать их можно как
систему двух вдвинутых одна в другую
ионных подрешеток. При наложении на
ионный кристалл электрического поля
происходит некоторая деформация
кристаллической решетки или
относительное смещение подрешеток,
приводящее к возникновению дипольных
моментов.
Таким
образом, внесение всех трех групп
диэлектриков во внешнее электрическое
поле приводит к возникновению отличного
от нуля результирующего электрического
момента диэлектрика, или, иными словами,
к поляризации диэлектрика. Поляризацией
диэлектрика
называется процесс ориентации диполей
или появления под воздействием
электрического поля ориентированных
по полю диполей.
Соответственно
трем группам диэлектриков различают
три вида поляризации:
электронная,
или деформационная, поляризация
диэлектрика
с неполярными молекулами, заключающаяся
в возникновении у атомов индуцированного
дипольного момента за счет деформации
электронных орбит;
ориентационная,
или
дипольная, поляризация диэлектрика
с полярными молекулами, заключающаяся
в ориентации имеющихся дипольных
моментов молекул по полю. Естественно,
что тепловое движение препятствует
полной ориентации молекул, но в результате
совместного действия обоих факторов
(электрическое поле и тепловое
движение) возникает преимущественная
ориентация дипольных моментов молекул
по полю. Эта ориентация тем сильнее, чем
больше напряженность электрического
поля и ниже температура;
ионная
поляризация диэлектриков
с ионными кристаллическими решетками,
заключающаяся в смещении подрешетки
положительных ионов вдоль поля, а
отрицательных — против поля, приводящем
к возникновению дипольных моментов.
Соседние файлы в папке Трофимова Курс физики
- #
16.03.2016155.65 Кб1141.doc
- #
16.03.2016662.53 Кб21210.doc
- #
16.03.2016592.38 Кб25111.doc
- #
- #
16.03.2016181.76 Кб16913.doc
- #
16.03.2016336.38 Кб13614.doc
- #
16.03.2016206.34 Кб14115.doc
- #
16.03.2016169.98 Кб10116.doc
|
Потенциал. Разность потенциалов. Напряжение. |
|
|
Потенциал электростатического поля — скалярная величина, равная отношению потенциальной энергии заряда в поле к этому заряду: — энергетическая характеристика поля в данной точке. Потенциал не зависит от величины заряда, помещенного в это поле. |
|
|
Т.к. потенциальная энергия зависит от выбора системы координат, то и потенциал определяется с точностью до постоянной. За точку отсчета потенциала выбирают в зависимости от задачи: а) потенциал Земли, б) потенциал бесконечно удаленной точки поля, в) потенциал отрицательной пластины конденсатора. |
|
|
— следствие принципа суперпозиции полей (потенциалы складываютсяалгебраически). |
|
|
Потенциал численно равен работе поля по перемещению единичного положительного заряда из данной точки электрического поля в бесконечность. В СИ потенциал измеряется в вольтах: |
|
|
Разность потенциалов |
|
|
|
|
|
Напряжение — разность значений потенциала в начальной и конечнойточках траектории. Напряжение численно равно работе электростатического поля при перемещении единичного положительного заряда вдоль силовых линий этого поля. Разность потенциалов (напряжение) не зависит от выбора системы координат! |
|
|
Единица разности потенциалов
Напряжение равно 1 В, если при перемещении положительного заряда в 1 Кл вдоль силовых линий поле совершает работу в 1 Дж. |
|
|
Связь между напряженностью и напряжением. |
|
|
Из доказанного выше: напряженность равна градиенту потенциала (скорости изменения потенциала вдоль направления d). |
|
|
Из этого соотношения видно:
|
|
|
Эквипотенциальные поверхности. ЭПП — поверхности равного потенциала. Свойства ЭПП: — работа при перемещении заряда вдоль эквипотенциальной поверхности не совершается; — вектор напряженности перпендикулярен к ЭПП в каждой ее точке. |
|
|
|
|
|
Измерение электрического напряжения (разности потенциалов) Между стержнем и корпусом — электрическое поле. Измерение потенциала кондуктора Измерение напряжения на гальваническом элементе Электрометр дает большую точность, чем вольтметр. |
|
|
Потенциальная энергия взаимодействия зарядов. |
|
|
|
|
|
Потенциал поля точечного заряда |
|
|
|
|
|
Потенциал заряженного шара а) Внутри шара Е=0, следовательно, потенциалы во всех точках внутри заряженного металлического шара одинаковы (!!!) и равны потенциалу на поверхности шара. б) Снаружи поле шара убывает обратно пропорционально расстоянию от центра шара, как и в случае точечного заряда. |
|
|
Перераспределение зарядов при контакте заряженных проводников. Переход зарядов происходит до тех пор, пока потенциалы контактирующих тел не станут равными. |
Обновлено: 26.05.2023
Для определения разности потенциалов поля некоторых заряженных тел воспользуемся формулами их напряженностей Е (раздел 1.9) и соотношением .
1. Поле равномерно заряженной бесконечной плоскости с поверхностной плотностью заряда +s. . Потенциал данного поля меняется только в направлении х, поэтому ; ; . Проинтегрируем обе части равенства ; , где х1 и х2 — расстояния от точек 1 и 2 до плоскости.
2. Поле двух бесконечных параллельных разноименно заряженных плоскостей (+s и -s).
Напряженность поля между пластинами , отсюда ; .
При расстоянии между пластинами равном d, их разность потенциалов равна ; .
Установленная связь между напряженностью поля и потенциалом позволяет по известной напряженности поля найти разность потенциалов между двумя произвольными точками этого поля.
1. Поле равномерно заряженной бесконечной плоскости определяется формулой Е=, где — поверхностная плотность заряда. Разность потенциалов между точками, лежащими на расстояниях xi и х2 от плоскости (используем формулу (1.22)), равна
2. Поле двух бесконечных параллельных разно
именно заряженных плоскостей определяется формулой Разность потенциалов между плоскостями, расстояние между которыми равно d (см. (1.22)), равна
3. Поле равномерно заряженной сферической поверхности радиуса R с общим зарядом Q вне сферы (г > R) вычисляется
Разность потенциалов между двумя точками, лежащими на расстояниях п и г2 от центра сферы (г> > R, r2 > R), равна
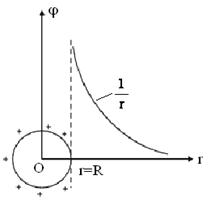 Рис. 15 |
Если принять и то потенциал поля внесферической поверхности задается выражением (ср. с формулой (1.19)). График зависимости приведен на рис. 15 |
4. Поле равномерно заряженного цилиндра радиуса R,
заряженного с линейной плотностью х, вне цилиндра (г > R) определяется формулой . Следовательно, разность потенциалов между двумя точка-
ми, лежащими на расстояниях и от оси заряженного цилиндра (r>R, r>R), равна
Установленная связь между напряженностью поля и потенциалом позволяет по известной напряженности поля найти разность потенциалов между двумя произвольными точками этого поля.
1. Поле равномерно заряженной бесконечной плоскости определяется формулой Е=, где — поверхностная плотность заряда. Разность потенциалов между точками, лежащими на расстояниях xi и х2 от плоскости (используем формулу (1.22)), равна
2. Поле двух бесконечных параллельных разно
именно заряженных плоскостей определяется формулой Разность потенциалов между плоскостями, расстояние между которыми равно d (см. (1.22)), равна
3. Поле равномерно заряженной сферической поверхности радиуса R с общим зарядом Q вне сферы (г > R) вычисляется
Разность потенциалов между двумя точками, лежащими на расстояниях п и г2 от центра сферы (г> > R, r2 > R), равна
 Рис. 15 |
Если принять и то потенциал поля внесферической поверхности задается выражением (ср. с формулой (1.19)). График зависимости приведен на рис. 15 |
4. Поле равномерно заряженного цилиндра радиуса R,
заряженного с линейной плотностью х, вне цилиндра (г > R) определяется формулой . Следовательно, разность потенциалов между двумя точка-
ми, лежащими на расстояниях и от оси заряженного цилиндра (r>R, r>R), равна
Связь между напряженностью и разностью потенциалов является важной темой в разделе физики под названием электродинамика. Ее можно установить, используя представление об эквипотенциальных поверхностях, а также характер каждой из частей по отдельности. Кроме того, важно знать основные формулы напряженности и других электродинамических параметров.
Разность потенциалов
Для того чтобы понять связь между напряженностью и потенциалом, нужно рассмотреть некоторые определения. Так, указанный параметр представляет собой скалярную величину, какая равна соотношению между энергией заряда в поле к непосредственно заряду. То есть, f=W/q есть энергетический тип характеристики поля в определенной точке. Для разности потенциалов формула имеет вид U=f1-f2=A/q. Здесь A является работой, затрачиваемой на переходы зарядного элемента по поверхности, а q есть кулоновский заряд.
При этом электростатическая величина не зависит от количества заряда, каков находится в поле. То есть, энергия будет зависеть от выбора координатной системы и находится с точностью до постоянной. В зависимости от условий задачи за начало отсчета выбирается один из рассматриваемых вариантов:
- Потенциал планеты Земля.
- Бесконечно удаленная точка поля, которой можно обозначить любую часть пространства.
- Отрицательная пластина емкостного или аналогичного конденсатора.
Численно он будет равняться работе по перемещению единичного плюсового заряда из точки электрического поля через бесконечность. Единица измерения указанного электрического параметра выражается в вольтах.
Разность потенциалов это в физике есть напряжение, которое также входит в раздел электрической динамики. Под ним понимают разницу значений в начальной и финальной точке траектории. Оно численно эквивалентно работе электростатического поля при перемещениях единичного положительного заряда вдоль силовых линий.
Физическая связь
Формула напряженности имеет вид E=U/delta (d). Это обозначает скорость изменения параметра вдоль направления d. Из указанного соотношения можно отметить:
- Вектор напряженности всегда направляется на уменьшение электрического и динамического потенциалов.
- Электрическое поле появляется в те моменты, когда можно связать разность потенциалов.
- Напряженность поля равняется соотношению вольта к метру, если между 2 точками на расстоянии 1 м друг от друга имеется разность в 1 В.
Для равномерно распределенного показателя важно наличие эквипотенциальных поверхностей. Их свойства заключаются в том, что работа при перемещении заряда вдоль такой поверхности не происходит, а вектор напряженности перпендикулярно расположен к ЭПП в любой точке.
Именно благодаря такому параметру можно отыскать некоторые физические величины. Напряженность помогает установить изменение скорости потенциального перемещения вдоль линий магнитного поля во времени. Энергетические характеристики используют в других разделах электродинамики и физики.
Неоднозначность определения
Так как величина определяется с точностью до произвольной постоянной (при этом все величины не изменятся), физический смысл имеет только разность, а не сама физическая единица.
При этом все остальные заряды по модулю при таких операциях как бы заморожены. Перемещение чаще всего воображаемое, хотя если остальные заряды закреплены или пробный очень мал, и при этом переносится относительно быстро, то формула определения разности потенциальных изменений верна.
Иногда для того, чтобы убрать неоднозначность, стоит применить некоторые естественные условия. Нередко такую физическую величину определяют так, чтобы она была равна нулю на бесконечности для любого числа точечных зарядов. Тогда для всех конечных систем зарядов выполнится аналогичное условие, а над константой можно не особо задумываться и принимать любую точку.
Также некоторые сложности имеются при употреблении терминов напряжение и электрический потенциал. Они имеют разный смысл, при этом нередко употребляются как синонимичные для электростатического потенциала. При неимении изменяющихся магнитных полей напряжение будет равняться разности потенциалов.
Рассмотрим несколько примеров вычисления разности потенциалов между точками поля, созданного некоторыми заряженными телами.
Разность потенциалов между точками поля, образованного двумя бесконечными заряженными плоскостями
Мы показали, что напряженность связана с потенциалом
где – напряженность электростатического поля между заряженными плоскостями, найденная в п. 2.5.2 с помощью теоремы Остроградского–Гаусса; σ = q/S– поверхностная плотность заряда.
Теперь, чтобы получить выражение для потенциала между плоскостями, проинтегрируем выражение (3.7.1):
На рисунке 3.5 изображена графическая зависимость напряженности E и потенциала φ от расстояния между плоскостями.
Разность потенциалов между точками поля,образованного бесконечно длинной цилиндрической поверхностью
В п. 2.5 с помощью теоремы Остроградского-Гаусса мы показали, что, т.к. , то (см. рис. 3.6)
Т.к. то , отсюда найдем разность потенциалов в произвольных точках 1 и 2:
На рисунке 3.6 изображена зависимость напряженности E и потенциала от r. (Здесь и далее E – изображена сплошной линией, а – пунктирной).
Разность потенциалов между обкладками цилиндрического конденсатора
В п. 2.5. мы нашли, что (рис. 3.7)
Отсюда так же, как и в предыдущем случае, разность потенциалов будет равна:
Таким образом, внутри меньшего цилиндра имеем , Е = 0, между обкладками потенциал уменьшается по логарифмическому закону, а вторая обкладка (вне цилиндров) экранирует электрическое поле и φ и Е равны нулю.
На рисунке 3.7 изображена зависимость напряженности E и потенциала от r.
Разность потенциалов между точками поля, образованного заряженной сферой (пустотелой)
Напряженность поля сферы (рис. 3.8) определяется формулой: .
Разность потенциалов внутри диэлектрического заряженного шара
Имеем диэлектрический шар (рис. 3.9), заряженный с объемной плотностью
В п. 2.5 с помощью теоремы Остроградского–Гаусса мы нашли, что внутри шара .
Теперь найдем разность потенциалов внутри шара:
Отсюда находим потенциал шара:
Из полученных соотношений можно сделать следующие выводы.
С помощью теоремы Гаусса сравнительно просто можно рассчитать Е и φ от различных заряженных поверхностей.
Напряженность поля в вакууме изменяется скачком при переходе через заряженную поверхность.
Потенциал. Разность потенциалов. ЗАДАЧИ с решениями
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача № 1. Металлический шар диаметром d заряжен с поверхностной плотностью зарядов σ. Найти потенциал φ этого шара, если он окружен заземленной проводящей сферой, имеющей общий с шаром центр. Диаметр сферы D. Среда — воздух.
Задача № 2. Потенциал заряженного шара φ1 = 300 В. Чему равен потенциал φ2 электрического поля этого шара в точке, отстоящей на расстоянии l = 50 см от его поверхности, если радиус шара R = 25 см?
Задача № 3. Определить потенциал φ точки поля, находящейся на расстоянии а = 9 см от поверхности заряженного шара радиусом R = 1 см, если поверхностная плотность зарядов на шаре σ = 1 • 10 –11 Кл/см 2 . Среда — воздух.
Задача № 4. В точке 1 поля точечного заряда-источника потенциал φ1 = 40 В, а в точке 2 φ2 = 10 В. Найти потенциал φ в точке М, лежащей посередине между точками 1 и 2 (рис. 3-6).
Задача № 5. В трех вершинах квадрата со стороной а = 20 см находятся заряды q1 = 1 • 10 –8 Кл, q2 = 2 • 10 –8 Кл и q3 = 2 • 10 –8 Кл (рис. 3-7). Определить потенциал φ электрического поля, созданного этими зарядами в четвертой вершине.
Задача № 6. Четыре одинаковых точечных заряда q расположены на одной прямой на расстоянии r друг от друга. Какую работу А надо совершить, чтобы переместить эти заряды в вершины тетраэдра со стороной r? Среда — вакуум.
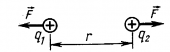
Задача № 7. Два одинаково заряженных шарика диаметрами d = 0,5 см каждый расположены на расстоянии l = 2 см между их поверхностями (рис. 3-14). До какого потенциала φ они заряжены, если сила их отталкивания друг от друга F = 2 мкН? Среда — воздух.
Задача № 8. В однородном электрическом поле напряженностью Е = 2 кВ/см переместили заряд q = –20 нКл в направлении силовой линии поля на расстояние d = 10 см. Найти работу поля А, изменение потенциальной энергии поля ΔWп и напряжение (разность потенциалов) U между начальной и конечной точками перемещения.
Задача № 9. Между двумя горизонтальными плоскостями, заряженными разноименно и расположенными на расстоянии d = 5 мм друг от друга, находится в равновесии капелька масла массой 20 нг (нанограмм) (рис. 3-10). Найти число избыточных электронов N на этой капельке. Среда — воздух. Разность потенциалов между плоскостями U = 2 кВ.
Задача № 10. На пластине М поддерживается потенциал φ1 = +80 В, а на пластине N – φ2 = –80 В (рис. 3-11, а). Расстояние между пластинами d = 10 см. На расстоянии d1 = 4 см от пластины М помещают заземленную пластину Р (рис. 3-11, б). Найти изменение напряженности ΔЕ1 поля на участке МР и изменение напряженности поля ΔЕ2 на участке PN при этом. Построить графики зависимостей напряженностей Е = Е(х) и потенциала φ = φ(х) от расстояния между точками поля и пластинами.
Читайте также:
- Макс корж биография кратко
- Отечественная и иностранная статистика мирового хозяйства кратко
- Гоголь и театр кратко
- Стричь под одну гребенку значение фразеологизма и происхождение кратко
- Свидетель это кратко и понятно
№
37. Связь между напряженностью и разностью потенциалов электрического поля.
Напряженность
электрического поля – величина, численно равная силе, действующей на заряд.
Потенциал φ – величина, численно равная
потенциальной энергии заряда.
Каждой точке
электрического поля соответствуют определенные значения потенциала и напряженности.
Найдем связь напряженности электрического поля с потенциалом.
Пусть заряд q перемещается
в направлении вектора напряженности однородного электрического поля из точки 1 в точку 2,
находящуюся на расстоянии от точки 1 (рис.93, стр. 119).
Электрическое поле совершает работу: A=qEΔd
Эту работу согласно формуле можно выразить через
разность потенциалов в точках 1 и 2: A=qU
Приравнивая выражения для работы, найдем модуль
вектора напряженности поля:
qEΔd=qU
E= =
Где U —
разность потенциалов между точками 1 и 2, которые
связаны вектором перемещения , совпадающим по направлению с вектором напряженности
.
Формула E=
показывает: чем меньше меняется потенциал на
расстоянии , тем меньше напряженность электростатического
поля. Если потенциал не меняется совсем, то напряженность поля равна нулю.
Так как при
перемещении положительного заряда в направлении вектора напряженности электростатическое поле совершает
положительную работу , то потенциал
больше потенциала
.
Следовательно, напряженность
электрического поля направлена в сторону убывания потенциала.
Любое
электростатическое поле в достаточно малой области пространства можно считать
однородным. Поэтому формула E= справедлива
для произвольного электростатического поля, если только расстояние настолько мало, что изменением
напряженности поля на этом расстоянии можно пренебречь.
Единица напряженности
электрического поля. Единицу напряженности электрического поля в СИ
устанавливают, используя последнюю формулу . Напряженность
электрического поля численно равна единице, если разность потенциалов между
двумя точками на расстоянии 1 м в однородном поле равна 1
В. Наименование этой единицы — вольт на метр (В/м).
Напряженность можно
также выражать в ньютонах на кулон. Действительно,
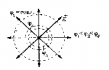
Эквипотенциальные поверхности.
Потенциал
электростатического поля представляет собой функцию, меняющуюся от точки к
точке. Однако, во всяком реальном случае можно выделить совокупность точек,
потенциалы которых одинаковы.
Геометрическое
место точек постоянного потенциала называется поверхностью равногопотенциала
или эквипотенциальной поверхностью.
Возьмем
равномерно заряженную бесконечную плоскость. Поле, создаваемое та
кой
плоскостью однородно, а линии напряженности нормальны к плоскости.
Отсюда
следует, что работа перемещения заряда из некоторой точки В1
в любую другую точку В2,
находящуюся на таком же расстоянии от заряженной поверхности, что и точка В1равна
нулю. Действительно, при перемещении некоторого заряда q по прямой В1
В2 сила, действующая на заряд со стороны поля, будет все время
перпендикулярна к перемещению, а, следовательно, ее работа равна нулю. Но
эта работа может быть представлена, с другой стороны, в виде:
A
= q(φ1— φ2)= 0
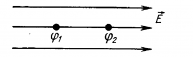
где
φ1 и φ2 – соответственно
потенциалы точек В1 и В2. Отсюда, так как
А
= 0, то φ1= φ2, т.е., потенциалы
точек, равноудаленных от заряженной
плоскости,
одинаковы. Таким образом, поверхности равного потенциала (эквипотенциальные
поверхности) являются плоскостями, параллельными заряженной плоскости. Если
плоскость заряжена положительно, то значение потенциала убывает по мере
удаления от заряженной плоскости. Очевидно, что поверхности равного потенциала
расположены симметрично по обе стороны от заряженной плоскости.
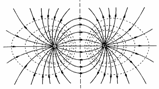
Эквипотенциальные
поверхности поля точечного заряда это сферы с радиусом
r,
центр которых находится в центре точечного заряда, т.е. φ=.
На
рисунке 95 вектор напряженности E перпендикулярен эквипотенциальным
поверхностям.
Покажем,
что вектор напряженности перпендикулярен эквипотенциальной поверхности.
Рассмотрим работу по перемещению заряда по поверхности равного потенциала
на малом участке пути ∆d. При этом, работа электрической
силы F=qE на данном пути будет:
A=F∆dcos
α= qE∆dcos
α, где α – угол между направлением силы f
и
перемещением ∆d. С другой стороны, эта работа может
быть выражена как произведение величины перемещающегося заряда на разность
потенциалов в начальном и конечном положениях заряда, т.е. A
= q(φ1— φ2)
Так
как перемещение идет по эквипотенциальной поверхности, то разность потенциалов (φ1—
φ2)=0 и qE∆dcos
α=0, или cosα= 0,
значит α = 900 т.е.
угол
между направлением силы F и
перемещением ∆d равен 900.
Но F и Е совпадают, поэтому угол
между E и ∆d, α=900, т.е.
направление вектора напряженности электростатического поля всегда
перпендикулярно к эквипотенциальной поверхности.
Значит, если провести поверхность,
перпендикулярную в каждой ее точке силовым линиям, то при перемещении заряда
вдоль этой поверхности работа не совершается. А это означает, что все точки
поверхности, перпендикулярной силовым линиям, имеют один и тот же потенциал.
Поверхности равного потенциала называют эквипотенциальными.
Эквипотенциальные
поверхности однородного
поля представляют собой плоскости (рис.94, стр. 120), а поля точечного
заряда — концентрические сферы (рис. 95, стр. 120).
Подобно силовым линиям, эквипотенциальные
поверхности качественно характеризуют распределение поля в пространстве. Вектор напряженности перпендикулярен
эквипотенциальным поверхностям и направлен в сторону уменьшения потенциала.
Эквипотенциальные
поверхности строятся обычно так, что разность потенциалов между двумя соседними
поверхностями постоянна. Поэтому согласно формуле расстояния между соседними
эквипотенциальными поверхностями увеличиваются по мере удаления от точечного
заряда, так как напряженность поля уменьшается.
Эквипотенциальные
поверхности однородного поля расположены на равных расстояниях друг от друга.
Эквипотенциальной является
поверхность любого проводника в электростатическом поле. Ведь силовые
линии перпендикулярны поверхности проводника. Причем не только поверхность, но
и все точки внутри проводника имеют один и тот же потенциал. Напряженность поля
внутри проводника равна нулю, значит, равна нулю и разность потенциалов между
любыми точками проводника.
Модуль напряженности электростатического поля
численно равен разности потенциалов между двумя близкими точками в этом поле,
деленной на расстояние между этими точками.
В однородном электрическом
поле напряженностью Е = 2*105 В/м
переместили заряд q = –20 нКл в направлении
силовой линии поля на расстояние d = 10 см. Найти работу
поля А, изменение потенциальной
энергии поля ΔWп и напряжение (разность
потенциалов) U между начальной и конечной
точками перемещения.
Домашнее
задание
§ 45-46,
вопросы.