Как найти разность потенциалов между сферами

Решение

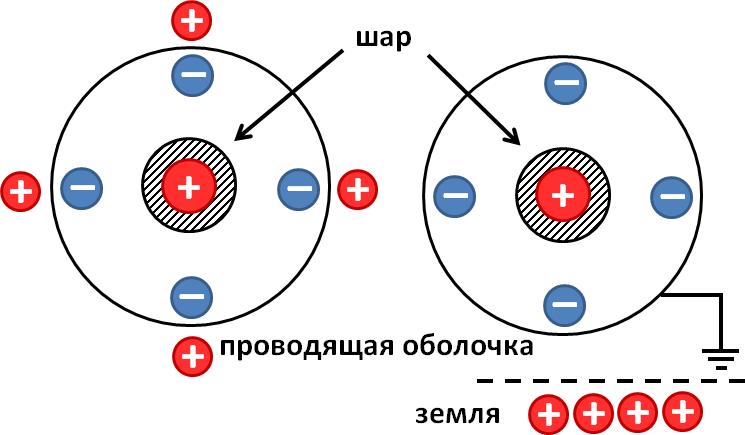
Внутри малой проводящей сферы напряженность поля все время равна нулю. Снаружи от большой сферы поле не зависит от положения точечного заряда — его силовые линии не выходят за внутреннюю поверхность большой сферы, а заряд внешней поверхности этой сферы распределен по ней равномерно и равен . По этой причине после соединения сфер проводником при перетекании зарядов с внутренней сферы на внешнюю поле снаружи не изменится.

Найдем начальные потенциалы сфер, которые равны сумме потенциалов, создаваемых всеми зарядами системы, в том числе и наведенными. Поскольку суммарные заряды каждой из сфер вначале равны нулю, то они не дают вклада в суммарный потенциал центральной точки системы, то есть ее потенциал определяется только зарядом и равен . Таким же будет и потенциал внутренней сферы, поскольку поле внутри нее равно нулю. Потенциал внешней сферы такой же, как и потенциал точечного заряда на расстоянии от него: . Таким образом, разность потенциалов между сферами

Если соединить сферы проводником, то их потенциалы сравняются. Пусть с внутренней сферы перетек на наружную заряд . Тогда суммарный заряд большой сферы станет равным , а малой — равным . Подсчитаем потенциал малой сферы и приравняем его к потенциалу большой сферы, который в процессе перетекания зарядов не изменяется. В центре малой сферы . Отсюда находим: .  

Ответ

Разность потенциалов между сферами перетекший заряд .

2020-02-12   

Две концентрические проводящие сферы не заряжены, а в пространстве между ними, на расстоянии $L$ от центра, закреплен точечный заряд $Q$. Найдите разность потенциалов между сферами. Какой заряд протечет по тонкому проводнику, если соединить этим проводником сферы?

Решение:

Потенциал внутренней сферы найти совсем просто — внутри сферы поле нулевое, тогда ее потенциал равен потенциалу центра сфер. Обе сферы вначале не заряжены, поэтому

$phi_{1} = phi_{ц} = k frac{Q}{L}$.

По внешней сфере под действием внутренних зарядов должны перераспределиться заряды — на ее внешней и внутренней поверхностях теперь появятся заряды (в сумме равные нулю). На внешней поверхности большой сферы заряд распределится равномерно, и поле снаружи будет таким, как если бы полный внутренний заряд системы был расположен в центре сфер. Тогда потенциал наружной сферы радиусом $R$ найдем по формуле для потенциала поля точечного заряда:

$phi_{2} = k frac{Q}{R}$.

Разность потенциалов между сферами составит

$Delta phi = phi_{1} — phi_{2} = kQ left ( frac{1}{L} — frac{1}{R} right )$.

После соединения сфер проводником по нему будут перетекать заряды, пока потенциалы сфер не станут равными. Пусть наружу перетечет полный заряд $q$, тогда заряд внутренней сферы станет равным $-q$, а внешняя сфера приобретет заряд $q$. Потенциал наружной сферы при этом не изменится (полный заряд системы при перетекании зарядов от одной сферы к другой не меняется), а потенциал внутренней сферы радиусом $r$ теперь станет

$phi = k frac{-q}{r} + k frac{Q}{L} + k frac{q}{R} = phi_{2} = k frac{Q}{R}$.

Отсюда найдем перетекший по проводнику заряд:

$q = Q frac{ frac{1}{L} — frac{1}{R} }{ frac{1}{r} — frac{1}{R} }$.

Содержание книги

Предыдующая страница

§11. Постоянный электрический ток

11.8 Электрическое сопротивление среды при пространственно распределенных токах.

Электрический ток может протекать не только «концентрировано», по проводам. Движение электрических зарядов может занимать определенную область проводника, при этом векторное поле плотности тока (~vec j(x,y,z)) , не обязательно является однородным, а представлять достаточно сложную структуру. Расчет электрического сопротивления между различными точками среды в этом случае принципиально отличается от рассмотренных выше. Особо отметим, что электрическое сопротивление среды зависит не только от ее свойств (удельного электрического сопротивления), но и от распределения токов в среде. Проиллюстрируем это положения двумя примерами, заодно и покажем методы расчета сопротивления для пространственно распределенных токов.

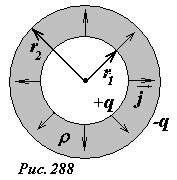
Пример 1. Пространство между двумя концентрическими хорошо проводящими сферами радиусами r₁ и r₂ заполнено слабопроводящим веществом с удельным электрическим сопротивлением ρ (рис. 288). Определим сопротивление среды между сферами.

Оговорки о проводимости сфер и среды между ними позволяют использовать следующие приближения:

— считать потенциалы сфер постоянными и пренебречь их сопротивлением;

— пренебречь объемными зарядами в пространстве между сферами, которые, в принципе, могут возникать при протекании электрического тока.

Для расчета сопротивления среды между сферами положим, что на внутренней сфере поддерживается постоянный электрический заряд +q (то есть сфера подключена к источнику тока, который компенсирует заряд, стекающий с него через проводящую среду). Электрическое поле в пространстве между сферами эквивалентно полю точечного заряда +q, помещенного в центр сфер. Следовательно, разность потенциалов между сферами может быть рассчитана по знакомой из электростатики формуле

(~Delta varphi = frac{q}{4 pi varepsilon_0} left ( frac{1}{r_1} — frac{1}{r_2} right )) . (1)

Так как система обладает сферической симметрией, то вектор плотности электрического тока (~vec j) во всех точках направлен радиально (вдоль прямой проходящей через центр сфер).

Задание для самостоятельной работы.

1. Докажите, что модуль вектора плотности тока убывает обратно пропорционально квадрату расстояния до центра сфер.

Непосредственно у поверхности внутренней сферы напряженность электрического поля равна

(~E = frac{q}{4 pi varepsilon_0 r^2_1}) . (2)

По закону Ома плотность тока у поверхности сферы равна

(~j = frac{1}{rho} E = frac{q}{4 pi varepsilon_0 rho r^2_1}) . (3)

Так как вектор плотности тока направлен радиально, то есть по нормали к поверхности сферы, и постоянен по модулю, то сила электрического тока, стекающего со сферы, равная потоку вектора плотности тока, равна произведению плотности тока на площадь сферы (~I = jS = frac{1}{rho} E = frac{q}{4 pi varepsilon_0 rho r^2_1} cdot 4 pi r^2_1 = frac{q}{varepsilon_0 rho}) . Зная силу тока и разность потенциала, электрическое сопротивление рассматриваемой системы определим по закону Ома

(~R = frac{Delta varphi}{I} = frac{rho}{4 pi} left ( frac{1}{r_1} — frac{1}{r_2} right ) = frac{rho(r_2 — r_1)}{4 pi r_2 r_1}) . (4)

Как и следовало ожидать, полученное значение сопротивления не зависит от «придуманного» заряда внутренней сферы.

Итак, суть использованного метода сводится к независимому расчету разности потенциалов и силы тока между сферами, при заданном значении заряда сферы. Величина этого заряда сокращается при вычислении сопротивления.

Интересно отметить, что если расстояние между сферами Δr = r₂ — r₁ значительно меньше их радиусов, то в знаменателе формулы (4) можно пренебречь различием в их радиусах, тогда знаменатель упрощается (~4 pi r_2 r_1 approx 4 pi r^2 = S) , то есть становится равным площади поверхности сферы. В этом случае полученная формула (4) превращается в банальную (~R = rho frac{l}{S}) .

Если радиус внешней сферы устремить к бесконечности ((~r_2 to infty, frac{1}{r_2} to 0)), то рассматриваемая система превращается в заряженный шарик, помещенный в бесконечную проводящую среду. В этом случае сопротивление среды от шарика радиуса r до «бесконечности» оказывается равным

(~R = frac{rho}{4 pi r}) . (5)

Пример 2. Два одинаковых металлических шарика, радиусы которых равны r, находятся на большом расстоянии a (a >> r) друг от друга в слабопроводящей среде с удельным электрическим сопротивлением ρ (рис. 289). Вычислим электрическое сопротивление среды между шариками.

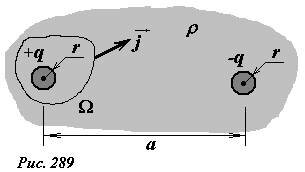
Для расчета электрического сопротивления мысленно сообщим шарикам электрические заряды, равные по величине и противоположные по знаку (+q,-q). Так расстояние между шариками значительно больше размеров шарика, то можно пренебречь влиянием заряда одного шарика потенциал другого, тогда разность потенциалов между шариками определяется по формуле

(~Delta varphi = varphi^+ — varphi^- = frac{+q}{4 pi varepsilon_0 r} — frac{-q}{4 pi varepsilon_0 r} = frac{q}{2 pi varepsilon_0 r}) , (6)

где φ⁺, φ^— — потенциалы положительно и отрицательно заряженных шариков, соответственно.

Распределение напряженности электрического поля (и соответствующей ему плотности тока) в данном случае достаточно сложной ^[1]. Однако для вычисления силы тока, стекающего с одного из шариков, знание его не требуется. Мысленно окружим положительно заряженный шарик произвольной замкнутой поверхностью Ω. Поток вектора плотности тока через эту поверхность и будет равен суммарной силе тока между шариками (~I = Phi_{vec j}) . По закону Ома плотность тока пропорциональна напряженности электрического поля (~vec j = frac{1}{rho} vec E) ; так как поток пропорционален этому вектора, то такое же соотношение будет выполняться и для потоков векторов плотности тока и напряженности поля (~Phi_{vec j} = frac{1}{rho} Phi_{vec E}) . Для потока вектора напряженности электрического поля справедлива теорема Гаусса (~Phi_{vec E} = frac{q}{varepsilon_0}) . Таким образом, сила тока между шариками выражается элементарно

(~I = Phi_{vec j} = frac{1}{rho} vec E = frac{q}{rho varepsilon_0}) . (7)

Теперь легко вычислить искомое сопротивление

(~R = frac{Delta varphi}{I} = frac{rho}{2 pi r}) . (8)

Задания для самостоятельной работы.

1. В каком месте при выводе формулы (8) мы учли, что ток идет между шариками?
2. Получите более точную формулу для сопротивления между шариками с учетом расстояния между ними (не полагая его бесконечно большим).

Теперь, внимание! Сравним два результата, формулы (5) и (8) – сопротивления, рассчитанные по этим формулам, отличаются в два раза, хотя, и в одном и другом случае рассматривается стекание тока с металлического шарика в неограниченную среду. Причина такого существенного расхождения заключается в различной структуре поля электрических токов – если в первом случае ток растекается радиально, одинаково во все стороны, то во втором ток преимущественно направлен в одну сторону, ко второму шарику. Тем самым, мы наглядно продемонстрировали, что электрическое сопротивление зависит не только от свойств среды и размеров источника, но и распределением токов.

Примечания

1. ↑ Оно соответствует полю двух точечных зарядов, рассмотренному и нарисованному ранее.

Следующая страница

Примеры решения задач по физике — концентрические проводящие сферы

Суббота, 25 февраля, 2012

Среди школьных задач по физике особняком стоят те, которые связаны с концентрическими проводящими сферами. Эти сферы могут быть заряжены, заземлены, могут находиться в поле внешних зарядов и т. д., вариаций много. В школьном курсе физики эти задачи являются одними из самых сложных. Не в последнюю очередь, конечно, непонимание данного материала связано с неспособностью учителей объяснить его грамотно и доступно. Итак, попробуем разобраться, что это за проводящие сферы и с чем их едят.

Тексты заданий я взял из сборника задач по физике для подготовительных отделений вузов.

Задача 1. Сфера радиуса r, которой сообщен заряд q, окружена концентрической тонкостенной проводящей сферической оболочкой радиуса R, заряд которой равен Q. Определите потенциалы сфер φ_in (внутренней) и φ_ex (внешней).

Решение. Потенциал на поверхности внутренней сферы φ_ex складывается из двух потенциалов: внешней сферы φ₁ и собственно внутренней сферы φ₂.

Потенциал внешней сферы φ₁ в каждой точке ее внутреннего объема одинаков и равен потенциалу на ее поверхности (подробнее о решении задач на тему «Потенциал» читайте в этой статье):

Потенциал внутренней сферы φ₂ определяется известным соотношением:

Тогда общий потенциал φ_in на поверхности внутренней сферы равен:

Потенциал на поверхности внешней сферы также складывается из двух потенциалов: внутренней сферы φ’₁ и собственно внешней сферы φ’₂.

Потенциал внутренней сферы φ’₁ на расстоянии R от ее центра определяется известным соотношением:

Формула, определяющая потенциал внешней сферы φ’₂ на ее поверхности, также хорошо известна:

Тогда общий потенциал на поверхности внешней сферы равен:

Задача 2. Металлический шар радиуса R₁, заряженный до потенциала φ, окружают тонкой сферической проводящей оболочкой радиуса R₂. Определите потенциал шара φ₁ после того, как он будет соединен проводником с оболочкой. Первоначальный заряд оболочки равен нулю, центры оболочки и шара совпадают.

Решение. До соединения сфер проводником заряд первой был равен:

После соединения часть заряда с внутренней сферы перетекло на внешнюю. Ток прекратился в тот момент, когда потенциал шара стал равен потенциалу внешней оболочки. Удобнее поэтому искать не потенциал шара, а равный ему потенциал внешней оболочки. В соответствии с результатами, полученными в предыдущей задаче, этот потенциал определяется выражением:

где q₁ и q₂ — заряды шара и внешней оболочки после соединения их проводником соответственно. По закону сохранения заряда q = q₁ + q₂. После несложных преобразований получаем:

Задача 3. Металлический шар радиуса R₁, заряженный до потенциала φ, окружают концентрической сферической проводящей оболочкой радиуса R₂. Чему станет равен потенциал шара φ‘, если заземлить оболочку?

Начнем с рисунка к решению задачи:

Решение. Зная потенциал шара в начальный момент времени и его радиус, можно найти заряд на нем:

Вследствие явления электростатической индукции на внешней оболочке должно произойти разделение заряда. Отрицательный заряд перетечет на внутреннюю поверхность оболочки, положительный — на внешнюю (см. рисунок). Это же явление возникало и в предыдущих задачах, но мы не принимали его во внимание. Почему? В условии задач было указано, что оболочка тонкая, и такое «разбегание» зарядов не приводило к сколько-нибудь существенному изменению конфигурации электростатического поля.

В этой задаче учет данного явления важен, поскольку оболочку заземляют. После заземления положительный заряд с оболочки стечет на землю, останется лишь отрицательный q₂, поскольку он притягивается к положительному заряду q₁ внутренней сферы. Потенциал заземленной оболочки станет равен потенциалу земли, то есть нулю. В этой связи и в соответствии с результатом, полученным при решении первой задачи, получаем равенство:

Используя выражение для расчета потенциала внутренней сферы подобной системы, полученное в первой задаче, находим окончательно требуемый потенциал шара:

Опыт показывает, что редко кто понимает решение этих задач во всех деталях с первого раза. Обычно приходится долго и настойчиво разъяснять ученикам все те мелочи, без осознания которых решение сводится к пустым преобразованиям буквенных выражений с целью получения приведенного в конце учебника ответа. Понять физическую сущность этих задач и научиться применять полученные знания в будущем не просто. Однако в этом и состоит основная методическая ценность данной темы в школьном курсе физики. Лучшим помощником в ее изучении непременно станет профессиональный репетитор, грамотный наставник, который сможет придумать понятное именно вам объяснение и ответит на все возникшие вопросы. Кстати, если таковые имеются, вы можете задать их ниже в комментариях.

Репетитор по физике и математике
Сергей Валерьевич

Найти разность потенциалов между центром равномерно заряженной сферы и точкой, находящейся от центра на расстоянии двух радиусов сферы.