Существуют разные типы чисел — четные числа, нечетные числа, простые числа, составные числа. Также на основе знака числа могут быть двух видов —
положительные числа
и
отрицательные числа
. Эти числа могут быть представлены на числовой линией. Среднее число в этой строке равно нулю. С левой стороны от нуля находятся отрицательные числа, а с правой стороны — положительные.
Ноль — это нейтральный элемент относительно сложения целых чисел. В основном в этой статье мы будем изучать операции сложения и вычитания с отрицательными числами. Существуют определенные правила для знаков при сложении и вычитании:
- Для того чтобы сложить два отрицательных числа, надо сложить два числа и поставить знак минус.
((-2)+(-3)=-5)
- Если первое число положительное, а второе отрицательное, смотрим, какое число по модулю больше, отнимаем от большего меньшее число и ставим знак большего числа:
((-8)+4=4-8=-4)
(9+(-4)=9-4=5)
Для каждого числа кроме (0) существует противоположный элемент, при сумме с ним образуется ноль:
(-9+9=0) (7,1+(-7,1)=0)
- При вычитания двух чисел, в которых оба отрицательные, следует знать правило: минус на минус дает плюс. То есть, если стоят рядом два минуса, в сумме получается плюс.
((-7)-(-6)=(-7)+6=(-1))
- Если первое число положительное, а второе отрицательное, вычитаем по тому же принципу, что и складываем: смотрим, какое число по модулю больше, отнимаем от большего меньшее число и ставим знак большего числа.
(7-9=-2) так как (9>7)
- Также не стоит забывать минус на минус дает плюс:
(7-(-9)=7+9=16)
- (4+(-5))
- (-36+15)
- ((-17)+(-45))
- (-9+(-1))
Решение:
- (4+(-5)=4-5=-1)
- (-36+15=-21)
- ((-17)+(-45)) (=-17-45=-62)
- (-9+(-1)=-9-1=-10)
- (3-(-6))
- (-16-35)
- (-27-(-5))
- (-94-(-61))
Решение:
- (3-(-6)=3+6=9)
- (-16-35=-51)
- (-27-(-5)=-27+5=-22)
- (-94-(-61)=-94+61=-33)
Больше уроков и заданий по всем школьным предметам в онлайн-школе «Альфа». Запишитесь на пробное занятие прямо сейчас!
Запишитесь на бесплатное тестирование знаний!
Как вычесть отрицательные числа, сколько вариаций существует вычитания отрицательных чисел!?
Правила вычитания отрицательных чисел.
Всего возможных вариантов вычитания отрицательных чисел — 6. Все они имеют свои особенности. Для всех вариантов в данном пункте разберем все правила вычитания отрицательных чисел, а уже потом на каждое правило разберем примеры!
Правило вычитания отрицательных чисел:
В вычитании первое число называется уменьшаемое, второе вычитаемое, результат — разность.
1.1). Вычитание отрицательных чисел.
Если уменьшаемое a(без минуса) больше вычитаемого b(без минуса):
1.1.1). Правило для вычитания отрицательного числа из отрицательного числа:
Если уменьшаемое a без минуса больше вычитаемого b без минуса, то для данного подпункта есть отдельное правило:
Для вычитания отрицательного числа из отрицательного числа, нужно вынести минус за скобки, а внутри скобок произвести вычитание, как обычное вычитание.
если a > b -> -a — (-b) = — (a — b) = -с
Если уменьшаемое a(без минуса) меньше вычитаемого b(без минуса):
1.1.2). Правило для вычитания отрицательного числа из отрицательного числа:
Если уменьшаемое
a
без минуса
меньше
вычитаемого
b
без минуса, то для данного подпункта есть отдельное правило: положительное вычитаемое перемещаем на место уменьшаемого и вычитаем из него уменьшаемое :
если a < b -> -a — (-b) = b — a = с
1.2). Вычитание отрицательного числа из положительного.
Для данного подпункта, в двух случаях, когда уменьшаемое больше вычитаемого и наоборот, существует только одно правило:
Если из положительного уменьшаемого
a
вычесть отрицательное вычитаемое
(-b)
, то получим сумму уменьшаемого и вычитаемого.
a — (-b) = a + b = с
1.3). Вычитание положительного числа из отрицательного .
И для данного подпункта, в двух случаях, когда уменьшаемое больше вычитаемого и наоборот, существует только одно правило:
Если из отрицательного уменьшаемого
(-a)
вычесть положительное вычитаемое
b
, то получим сумму уменьшаемого и вычитаемого со знаком
минус
.
-a — b = -(a + b) = -с
Вычесть отрицательное число из отрицательного числа.
Для того, чтобы понять, как «Вычесть отрицательное число от отрицательного числа.«, вам потребуется правило:
Правило вычитания отрицательного числа из отрицательного числа:
-a — (-b) = -a + b = ± с
Чтобы из отрицательного числа «a» вычесть отрицательное висло «b» нужно открыть скобку числа «b», два минуса дадут плюс. Далее вам потребуется знание сложения отрицательного и положительного числа
Дополнение к «Правило вычитания отрицательного числа из отрицательного числа: «
Если в данном правиле число «a»(положительное) больше числа «b»(положительное), то знак вычитания будет отрицательным, например : «-15 — (-12)». Этот пример смотри ниже…
Если наоборот, то положительным.
Рассмотрим Правило вычитания отрицательного числа из отрицательного числа:
Для того, чтобы понять «Правило вычитания отрицательного числа из отрицательного числа» нам нужен пример! Возьмем те же числа , только первое будет тоже отрицательным :
Положительное число : — 15.
И отрицательное число : -12
У нас получились два отрицательных числа, и теперь, нам нужно от одного отрицательного числа вычесть другое отрицательное число :
-15 — (-12)
Как и раньше, мы должны открыть скобку. Минус на минус дает плюс :
-15 + 12 = -3
Как проверить правильность вычитания!?
Как проверить правильность вычитания отрицательного числа из отрицательного!?
Аналогично проверяем на на калькуляторе.

Вычесть отрицательное число от положительного числа.
Далее следующий пункт : как «Вычесть отрицательное число от положительного числа.«, нам понадобится пример, самый простой пример, пусть это будет :
Положительное число : 15.
И отрицательное число : -12
И от первого, будем отнимать второе, т.е. отнимем отрицательное от положительного числа, данное выражение должно быть записано таким образом:
15 — (-12)
В данном примере, если мы раскроем скобки, то получится наложение минуса на минс, что дает плюс.
15 — (-12) = 15 + 12 = 27
Как проверить правильность вычитания!?
Как проверить правильность вычитания отрицательного числа из положительного!?
Это можно сделать на калькуляторе.

Вычесть из отрицательного числа положительное число.
Теперь : как «Вычесть положительное число из отрицательного числа.«, числа все те же :
Положительное число : — 15.
И отрицательное число : 12
Третий вариант, будем вычитать положительное число из отрицательного :
-15 — 12
В таком случае. мы должны вынести минус за скобки и внутри скобок знаки поменяются на противоположные: :
-(15 + 12) = -27
Как проверить правильность вычитания!?
Как проверить правильность вычитания отрицательного числа из отрицательного!?
Аналогично проверяем на на калькуляторе.

Вычесть из отрицательного числа отрицательное число на калькуляторе.
Теперь вычтем отрицательные числа на калькуляторе :
-15 — (-12)
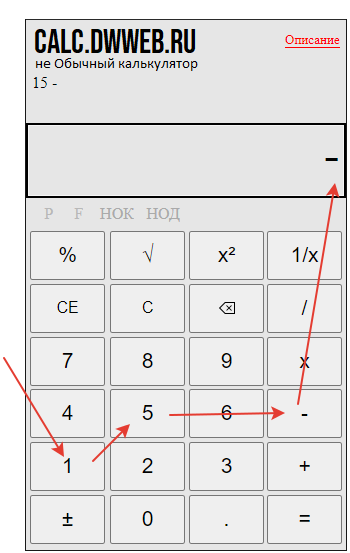
Набираем число 15.
Добавляем минус, нажимаем кнопку «±».
Нажимаем вычесть : «-«.
Набираем второе число : 12.
Добавляем минус, нажимаем кнопку «±».
Нажимаем равно -«=».
Получаем результат вычитания отрицательного числа из отрицательного:

Вычесть отрицательное число от положительного числа на калькуляторе.
У нас есть калькулятор, на котором будем вычитать отрицательное число из положительного числа
15 — (-12)
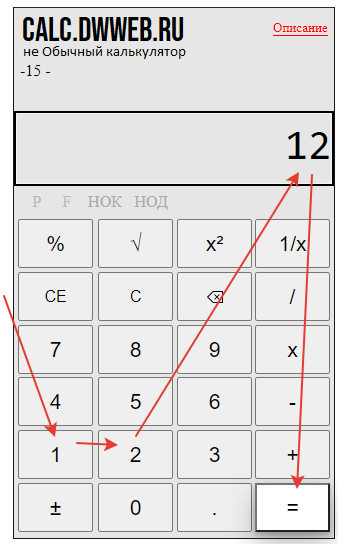
Набираем положительное число : 15.
Нажимаем кнопку минус : «-«.
Набираем второе число : 12.
Далее, чтобы данное число сделать отрицательным нажимаем кнопку «±», добавляем минус.
Далее нажимаем кнопку равно : «=».
Получаем результат вычитания отрицательного от положительного числа:

Вычесть из отрицательного числа положительное число на калькуляторе.
Для иллюстрации вычитания положительного числа из отрицательного, нам опять понадобится пример и калькулятор:
-15 — 12
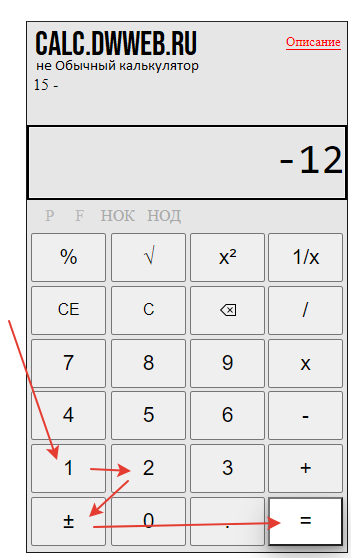
Набираем первое число : 15.
Добавляем перед ним минус, нажимаем кнопку «±».
Нажимаем кнопку вычесть : «-«.
Набираем второе число 12.
Нажимаем равно : «=».
Получаем результат вычитания положительного числа из отрицательного:

Как известно вычитание — это действие, противоположное сложению.
Если «a» и «b» — положительные числа,
то вычесть из числа «a» число «b», значит
найти такое число «c», которое при сложении
«с» числом «b» даёт число «a».
a − b = с или с + b = a
Определение вычитания сохраняется для всех рациональных чисел. То есть вычитание
положительных и отрицательных чисел можно заменить сложением.
Запомните!
Чтобы из одного числа вычесть другое, нужно к уменьшаемому прибавить число противоположное
вычитаемому.
Или по другому можно сказать, что вычитание числа «b» — это тоже самое сложение, но с числом
противоположным числу «b».
a − b = a + (−b)
Пример.
6 − 8 = 6 + (− 
Пример.
0 − 2 = 0 + (−2) = −2
Запомните!
Стоит запомнить выражения ниже.
0 − a = − a
a − 0 = a
a − a = 0
Правила вычитания отрицательных чисел
Как видно из примеров выше вычитание числа «b» — это сложение
с числом противоположным числу «b».
Это правило сохраняется не только при вычитании из бóльшего числа меньшего, но
и позволяет из меньшего числа вычесть большее число, то есть всегда можно найти
разность двух чисел.
Разность может быть положительным числом, отрицательным числом или числом ноль.
Примеры вычитания отрицательных и положительных чисел.
- −3 − (+ 4) = −3 + (−4) = −7
- −6 − (−7) = −6 + (+ 7) = 1
- 5 − (−3) = 5 + (+ 3) = 8
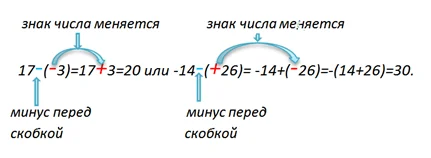
Удобно запомнить правило знаков, которое позволяет уменьшить количество скобок.
Знак «плюс» не изменяет знака числа, поэтому, если перед скобкой стоит плюс, то знак в скобках не меняется.
+ (+ a) = + a
+ (−a) = −a
Знак «минус» перед скобками меняет знак числа в скобках на противоположный.
Из равенств видно, что если перед и внутри скобок
стоят одинаковые знаки, то получаем «+», а если знаки разные, то
получаем «−».
(−6) + (+ 2) − (−10) −
(− 1) + (− 7) = −6 + 2 + 10 + 1 − 7 = − 13 + 13 = 0
Правило знаков сохраняется и в том случае, если в скобках не одно число, а
алгебраическая сумма чисел.
a − (− b + c) + (d − k + n) = a + b − c + d − k + n
Обратите внимание, если в скобках стоит
несколько чисел и перед скобками стоит знак «минус», то
должны меняться знаки перед всеми числами в этих скобках.
Чтобы запомнить правило знаков можно составить таблицу определения знаков числа.
Правило знаков для чисел
| + (+) = + | + (−) = − |
| − (−) = + | − (+) = − |
Или выучить простое правило.
Запомните!
Минус на минус даёт плюс.
Плюс на минус даёт минус.
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
6 июня 2015 в 12:10
Евгения Данилина
Профиль
Благодарили: 0
Сообщений: 4
Евгения Данилина
Профиль
Благодарили: 0
Сообщений: 4
температура воздуха иутром была +13. В течении дня она изменилась на -6. Найдите температуру воздуха вечером.
0
Спасибо
Ответить
1 июня 2016 в 14:02
Ответ для Евгения Данилина
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Т.к. изменение температуры воздуха указано с отрицательным значением, то температура снизилась на 6 градусов. А это значит, что +13-6=+7.
Ответ: температура воздуха вечером +7.
0
Спасибо
Ответить
План урока:
Сложение отрицательных чисел
Сложение чисел с разными знаками
Вычитание отрицательных чисел и чисел с разными знаками
В субботу, ученики 6 класса договорились встретиться и погулять в парке. Утром Юля выглянула в окошко, ярко светит солнышко, но при этом морозно. Девочка взглянула на термометр. Он показывал -10˚C. Мама попросила Юлю пойти на улицу немного позже, когда на улице потеплеет. Юля расстроилась и стала ждать. Через два часа девочка снова взглянула на термометр. Он показал -3. Ого! Всего два часа, а так потеплело – обрадовалась девочка и стала одеваться, чтобы идти гулять. В это время в комнату вошла мама и удивленно спросила «Уже потеплело? На сколько градусов?» Дочь не знала, что сказать и как правильно узнать, на сколько градусов стало теплее. Мама пришла на помощь и сообщила, что достаточно от -10 отнять -3, и мы узнаем, на сколько градусов изменилась температура воздуха за окном. Иначе, можно сказать, что шкала термометра поднялась вверх на 7 делений, значит, на улице стало теплее на 7 градусов. Запомнив все, что рассказала мама, Юля побежала в парк делиться новыми знаниями с друзьями.
Сложение и вычитание отрицательных чисел
Давайте вспомним любимую многими сказку «Буратино» и разберем задачу с участием любимых персонажей.
В театре Карабаса-Барабаса актерам жилось очень сложно, все куклы мечтали жить на свободе. Актеры тяжело работали, но долги перед хозяином росли с каждым днем. Злой владелец пообещал отпустить Буратино и Мальвину из своего театра только тогда, когда кукольные герои вернут ему долг. Сколько монет нужно собрать героям, чтобы оказаться на свободе, если у Буратино было -15 монет, а у Мальвины -6?
Чтобы ответить на главный вопрос задачи, нам нужно понимать, о чем идет речь. Изучив условие, возникает вопрос «Как может быть -15 и -6 монет?». В данном случае выходит, что Буратино и Мальвина должны вернуть Карабасу-Барабасу 15 и 6 монет, поэтому перед данными числами и стоит знак «минус». Получается, кукольные персонажи смогут покинуть театр, когда полностью вернут долг. Для этого необходимо узнать общий размер долга Буратино и Мальвины. Чтобы узнать размер долга, суммируем монеты персонажей -15 и -6. Но как их сложить, когда перед слагаемыми стоит «минус»? В подобных ситуациях применяют правило сложения отрицательных чисел.
Возвращаемся к решению задачи.
Теперь, правильно запишем и суммируем известные данные.
Получается, что герои имеют -21 монету, следовательно, они должны собрать 21 монету и вернуть долг, только тогда появится возможность покинуть театр Карабаса-Барабаса.
Источник
Рассмотрим еще одно задание.
Найдите результат сложения -24 и -16.
Чтобы вычислить сумму двух значений со знаком «минус», достаточно суммировать их модули, и перед полученной цифрой записать «-».
-24+(-16)=-(24+16)=-40.
Запомни! Если складываем два отрицательных числа, то суммируем их модули, а перед результатом сложения записываем «-».
Сложение чисел с разными знаками
Рассмотрим ситуацию.
Мишин папа навещал бабушку в деревне, обещал привезти гостинец сыну – яблоки. Во дворе Миша рассказал мальчишкам про папино обещание, и решил угостить яблоком, каждого из трех друзей, то есть, у него уже стало -3 яблока. Папа привез сыну 10 яблок и мальчик с радостью поделился фруктами с друзьями. Сколько яблок осталось у мальчика?
Чтобы найти количество яблок у мальчика, нам нужно узнать, чему равна сумма яблок –тех которые были у мальчика(-3), и тех, которые дал папа(10). То есть, чтобы ответить на главный вопрос задачи, достаточно сложить -3 и 10. Но слагаемые имеют разные знаки «+» и «-». Как же выполнить сложение положительного и отрицательного чисел? Запомнив алгоритм сложения положительных и отрицательных чисел сделать это, будет очень просто.
Используем рассмотренный алгоритм при выполнении действий.
Суммируем-3 и 10. Для этого:
- определяем модули: -3=|3|, 10=|10|;
- сравниваем модули, определяя больший: |3|<|10|;
- от большего отнимаем меньший: 10 – 3=7;
- так как по условию 10 – число положительное, то и результат будет числом положительным.
Записывается в таком виде:
-3+10=10 – 3=7.
Выходит, у мальчика стало 7 яблок.
Рассмотрим еще один пример сложения чисел с разными знаками.
Вычислите сумму -28 и 11.
Известные слагаемые имеют разные знаки, то есть -28 является значением отрицательным, а 11–положительным. Чтобы суммировать слагаемые, необходимо воспользоваться ранее рассмотренным алгоритмом. Вначале, определяем модули и сравниваем их.
-28=|28|;
11=|11|;
28>11.
Помним, что большее значение модуля имеет отрицательное слагаемое (-28), поэтому перед результатом нужно будет поставить знак «минус». Теперь, находим разность большего и меньшего значения модуля (28-17) и записываем математическое выражение:
-28+11=-(28-11)=-17.
Учитывая рассмотренные примеры, можно сказать, что:
любое числовое значение от прибавления к нему положительного числа, всегда становится больше, а от прибавления отрицательного числа только меньше.
Докажем справедливость данного правила, вычислив выражение и сравнив уменьшаемое с полученной суммой:-150+50.
Чтобы найти значение выражения нужно определить модули (150 и 50), оставив знак«-» модуля большего слагаемого, от большего значения отнимаем меньшее:
-150+50=-(150-50)=-100.
Сравним найденное значение выражения (-100) с уменьшаемым (-150), используя правило сравнения чисел с отрицательным знаком:
При сравнении цифровых значений со знаком «минус», меньшим будет то, чей модуль больше.
-150=|150|;
-100=|100|.
150>100;
-150<-100.
Действительно, при сложении с отрицательным числом уменьшаемое стало только меньше.
Вычитание отрицательных чисел и чисел с разными знаками
Мы уже знаем, как выполнять сложение и вычитание положительных и отрицательных чисел, но хочется сказать, что именно в этом разделе математики, большую роль играют противоположные числа. Для тех, кто забыл, напоминаем, какие числовые значения называются противоположными:
Если два числа отличаются только знаком, то они являются противоположными:-13 и 13, 141 и -141, 1000 и -1000.
Чтобы понять, какие правила необходимо соблюдать при выполнении вычитания чисел с разными знаками, давайте разберем задание.
Определите, чему будет равно значение выражения: от -510 отнять +210.
На первый взгляд задание очень простое и не вызывает никаких проблем. Но стоит записать разность в виде выражения:
-510-(+210)
Сразу возникает вопрос «Как вычитать, если уменьшаемое со знаком «минус», а вычитаемое со знаком «плюс»?».Чтобы решение подобных выражений не вызывало у вас трудностей, возьмите на заметку правило:
Чтобы выполнить вычитание чисел с разными знаками, нужно уменьшаемое оставить без изменений и прибавить к нему число, противоположное вычитаемому.
Например: -5-(+2).
Минус пять оставляем без изменений. Вычитаемое +2, а противоположное ему -2. Складываем уменьшаемое(-5) и число противоположное вычитаемому(-2): -5+(-2).
По правилу сложения отрицательных чисел, складываем модули(5+2) и ставим знак «-»:
-5+(-2)=-(5+2)=-7
Учитывая данное правило, получается, что к уменьшаемому(-510) необходимо прибавить значение,противоположное вычитаемому(210), таким числом будет -210:
Запишем выражение:
-510-(+210)=-510+(-210). Чтобы вычислить полученное выражение нужно сложить отрицательные значения, согласно правилу сложения отрицательных чисел:
-510-(+210)=-510+(-210)=-(510+210)=-720.
Вычисления окончены.
Источник
Рассмотрим следующее задание.
Найдите значение выражения: -248+248.
Используем правило сложения значений с разными знаками.
-248=|248|;
248=|248|;
248 – 248=0.
Следовательно, при сложении противоположных числовых значений в результате всегда будет 0.
Зная правило вычитания отрицательных чисел, можем сделать вывод, что знаки, стоящие перед скобками, могут менять знак числа, находящегося в скобках.
К примеру, в выражении 19-(-4), при вычислении используем правило, согласно которого, к уменьшаемому прибавляем, число противоположное вычитаемому, то есть знак вычитаемого «-» меняем на противоположный «+». Получим:
Запомни! Если перед скобкой в математическом выражении стоит знак «минус», то знак числа в скобках меняется на противоположный.
Ну а сейчас, разберем задание, в котором перед скобкой стоит знак «плюс».
Вычисли: -36+(-7).
В этом задании воспользуемся правилом сложения отрицательных чисел– сложим модули числовых значений, а перед суммой поставим знак «минус»:
Мы видим, что «плюс» перед скобкой никак не повлиял на знак числа, стоящего в скобках. Запомни! Если перед скобками стоит «плюс», то знак числового значения, стоящего в скобках никак не меняется.
В выполнении рассматриваемых действий нет ничего сложного. Главное запомнить основные требования и придерживаться их в процессе любых вычислений! Если сразу запомнить все правила не получается, заходи на сайт 100уроков.ru и мы всегда с удовольствием напомним нужное правило или алгоритм.
Минутка истории
История математики утверждает, что человечество длительное время не принимало ряд отрицательных числовых значений. Данный вид чисел, казался непонятным и ненужным. Привычных нам знаков «плюс» и «минус» просто не существовало. Если возникала необходимость в записи отрицательно числа, то его записывали следующим образом «долг в 30 монет». И лишь математики Древней Индии и Китая, выполняли записи отрицательных чисел без употребления слова «долг», а просто использовали черные чернила, вместо синих.
Только в 3 веке греческий ученый Диофант, стал обозначать знак «минус» вот таким символом .
Привычные нам знаки «+» и «-» появились в Германии в конце 15 века. Чешский ученый Ян Видман, отразил данные знаки в своей книге-пособии, помогающей подсчитывать прибыль и убытки чешским купцам. Стоит заметить, что данная книга была написана от руки и имела огромную популярность среди богатых людей того времени.
Основные правила сложения и вычитания положительных и отрицательных чисел
В зависимости от знака различают положительные и отрицательные числа. Их можно расположить на координатной прямой, где началом отсчета будет ноль, который не относится ни к положительным, ни к отрицательным значениям.
Определение
Положительные числа — это числа со знаком «+», который обычно не пишется. Положительные значения располагаются на числовой линии справа от нуля.
Определение
Отрицательные числа — это числа со знаком «−», расположенные слева от нуля на координатной прямой.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Основные правила сложения и вычитания отрицательных чисел:
- При сложении двух отрицательных чисел, необходимо суммировать их модули, затем перед полученным результатом приписать знак минус.
(-a;+;(-b);=;-;(vert-avert;+;vert-bvert);=;-;(a;+;b))
- Разность двух отрицательных чисел находится по правилу «минус на минус дает плюс».
((-a);-;(-b);=;(-a);+;b;=;b;-;a)
Сложение чисел с разными знаками
При складывании двух слагаемых, одно из которых с плюсом, а другое — с минусом, необходимо сравнить их модульные значения. От слагаемого с большим модулем нужно отнять слагаемое с меньшим модулем, далее перед полученным результатом поставить знак слагаемого, большего по модульному значению.
Примечание:
Каждая положительная величина имеет противоположный элемент с отрицательным символом. В сумме эти пары образуют 0:
(a;+;(-a);=;a;-;a;=;0)
Вычитание чисел с разными знаками
Вычитание положительных и отрицательных элементов обладает свойством, которое позволяет свести данное действие к сложению:
(а;–;b;=;a;+;(–b))
Расшифровка этой формулы дает следующее правило:
Вычитание одного числа из другого равно сумме уменьшаемого и числа, противоположного вычитаемому.
Для того, чтобы найти разность двух чисел с разными знаками, необходимо следовать алгоритму суммирования положительной и отрицательной величины: сравнить модули уменьшаемого и вычитаемого, из числа с большим модулем нужно вычесть меньшее модульное значение, затем перед полученным результатом поставить знак большего по значения.
Примеры упражнений
Пример 1.
Сложение двух отрицательных элементов:
− 89 + (− 125) = − (89 + 125) = − 214
Пример 2.
Вычитание двух отрицательных чисел:
− 134 − (− 357) = − 134 + 357 = 357 − 134 = 223
Пример 3.
Сложение двух чисел с разными знаками:
− 876 + 543
|− 876| > |543|
− 876 + 543 = − (|− 876| − |543|) = − (876 − 543) = − 333
Пример 4.
Вычитание двух элементов с разными знаками:
678 − 943
|678| < |− 943|
678 − 943 = − (|− 943| − |678|) = − (943 − 678) = − 265