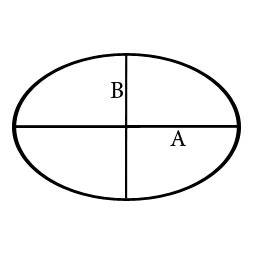
An ellipse is a two-dimensional curve on a plane that surrounds two focus points and is defined as the sum of the distances between the two focal points for every point on the curve. In other words, it’s a planar curve in which the total of the distances between its two focal points, or foci, is always the same from the given location. There are two sorts of axes in an ellipse, the major axis, and the minor axis. The main axis is the ellipse’s longest chord. The minor axis is orthogonal to the major axis and bisects the major axis in the middle.
How to find the Perimeter of an Ellipse?
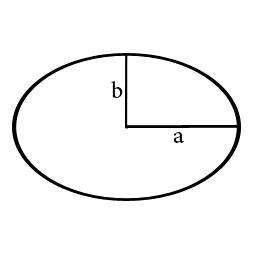
The perimeter of an ellipse is defined as its boundary length. To put it another way, it is equal to the length of the continuous line forming the boundary of the given ellipse. It can also be interpreted as the circumference of the ellipse. Its formula is equal to 2π (a constant) times the square root of the value of squares of its semi-minor and semi-major axis divided by 2. It is denoted by the symbol P.
The formula to find out the perimeter of ellipse is given by,
P = 2π √((a2 + b2) / 2))
where,
- a is the length of semi-major axis,
- b is the length of semi-minor axis.
How to find the Area of an Ellipse?
The area of an ellipse is defined as the amount of region occupied by it in a 2D space. It is denoted by the symbol A and its formula equals π (a constant) times the product of lengths of its semi-minor and semi-major axis.
The formula to calculate the area of an ellipse is:
A = πab
where,
- a is the length of semi-major axis,
- b is the length of semi-minor axis.
Sample Problems
Problem 1: Calculate the perimeter of an ellipse with a semi-major axis of 12 cm and a semi-minor axis of 10 cm.
Solution:
We have,
a = 12
b = 10
Using the formula we have,
P = 2π √((a2 + b2) / 2))
= 2π √((122 + 102) / 2))
= 2π √(244/2)
= 2 × 3.14 × 11.04
= 69.33 cm
Problem 2: Calculate the perimeter of an ellipse with a semi-major axis of 10 cm and a semi-minor axis of 7 cm.
Solution:
We have,
a = 10
b = 7
Using the formula we have,
P = 2π √((a2 + b2) / 2))
= 2π √((102 + 72) / 2))
= 2π √(149/2)
= 2 × 3.14 × 8.63
= 54.20 cm
Problem 3: Calculate the perimeter of an ellipse with a major axis of 14 cm and a minor axis of 12 cm.
Solution:
We have,
a = 14/2 = 7
b = 12/2 = 6
Using the formula we have,
P = 2π √((a2 + b2) / 2))
= 2π √((72 + 62) / 2))
= 2π √(85/2)
= 2 × 3.14 × 6.51
= 40.94 cm
Problem 4: Calculate the perimeter of an ellipse with a major axis of 18 cm and a minor axis of 10 cm.
Solution:
We have,
a = 18/2 = 9
b = 10/2 = 5
Using the formula we have,
P = 2π √((a2 + b2) / 2))
= 2π √((92 + 52) / 2))
= 2π √(106/2)
= 2 × 3.14 × 7.28
= 45.71 cm
Problem 5: Calculate the area of an ellipse with a semi-major axis of 8 cm and a semi-minor axis of 3 cm.
Solution:
We have,
a = 8
b = 3
Using the formula we have,
A = πab
= 3.14 × 8 × 3
= 75.36 sq. cm
Problem 6: Calculate the area of an ellipse with a semi-major axis of 16 cm and a semi-minor axis of 11 cm.
Solution:
We have,
a = 16
b = 11
Using the formula we have,
A = πab
= 3.14 × 16 × 11
= 552.64 sq. cm
Problem 7: Calculate the area of an ellipse with a major axis of 10 cm and a minor axis of 8 cm.
Solution:
We have,
a = 10/2 = 5
b = 8/2 = 4
Using the formula we have,
A = πab
= 3.14 × 5 × 4
= 62.8 sq. cm
Last Updated :
23 May, 2022
Like Article
Save Article
При помощи нашего калькулятора вы легко сможете узнать площадь эллипса.
Для того, что бы узнать площадь эллипса нам необходимо узнать длину двух полуосей или длину двух осей эллипса (максимальную и минимальную длину эллипса). После того как нам стали известны указанные величины мы можем применить формулу для расчета площади эллипса:
S= πab
формула для вычисления S – площади по полуосям a, b
S= πAB/4
формула для вычисления S – площади осям A, B
Где S – площадь, a и b – полуоси, A и B – оси эллипса, π – число Пи которое всегда примерно равно 3,14.
Загрузить PDF
Загрузить PDF
Эллипс — это фигура на плоскости, которая похожа на приплюснутый круг. Формула для нахождения площади эллипса напоминает выражение для площади круга. При этом следует помнить, что у эллипса два важных параметра: большая полуось и малая полуось.
-
1
Определите большую полуось эллипса. Это расстояние от центра эллипса до его самого дальнего края. Большую полуось можно представить себе в качестве максимального радиуса эллипса. Измерьте длину большой полуоси или найдите ее значение в условии задачи. Обозначим эту длину буквой a.
- Большая полуось эллипса является максимальным расстоянием от его центра до края.[1]
- Большая полуось эллипса является максимальным расстоянием от его центра до края.[1]
-
2
Определите малую полуось эллипса. Как можно догадаться по названию, это кратчайшее расстояние от центра эллипса до его края. Обозначим это расстояние латинской буквой b.
- Малая полуось эллипса расположена под прямым углом 90º к его большой полуоси, однако для нахождения площади нет необходимости определять углы.
- Малая полуось эллипса является минимальным расстоянием от его центра до края.
-
3
Умножьте на число «пи». Площадь эллипса равна a x b x π. Поскольку перемножаются две величины с размерностью длины, в ответе получится длина в квадрате.
- Например, если большая полуось эллипса равна 5 единицам, а малая 3 единицам длины, то получим площадь 5 x 3 x π, или около 47 квадратных единиц длины.
- Если у вас нет под рукой калькулятора или на калькуляторе нет символа π, используйте вместо этого числа значение «3,14».
Реклама
-
1
Вспомните формулу для площади круга. Вероятно, вы помните, что площадь круга равна πr2, то есть π x r x r. Что, если мы попробуем найти площадь круга по формуле для эллипса? В этом случае следует измерить радиус в одном направлении: r. Измерим радиус в перпендикулярном направлении, и тоже получим r. Подставим в формулу для площади эллипса: π x r x r! Таким образом, круг является лишь отдельной разновидностью эллипса.[2]
-
2
Представьте, что круг сплющили. Вообразите, что круг сжали до формы эллипса. По мере сжатия один радиус круга будет становиться все короче, а второй — длиннее. При этом площадь круга будет оставаться неизменной, поскольку ничто не покидает его и не добавляется к нему.[3]
Если мы используем в формуле для площади короткий и длинный радиусы, то «сплющивание» и «расширение» уравновесят друг друга, и в результате получится правильный ответ.Реклама
Советы
- Если вам требуется строгое доказательство, его можно получить с помощью интегрирования.[4]
Реклама
Об этой статье
Эту страницу просматривали 33 956 раз.
Была ли эта статья полезной?
Определение эллипсa
Определение.
Эллипс — это замкнутая плоская кривая, сумма расстояний от каждой точки которой до двух точек F1 и F2 равна постоянной величине. Точки F1 и F2 называют фокусами эллипса.
F1M1 + F2M1 = F1M2 + F2M2 = A1A2 = const
Элементы эллипсa
F1 и F2 — фокусы эллипсa
Оси эллипсa.
А1А2 = 2a — большая ось эллипса (проходит через фокусы эллипса)
B1B2 = 2b — малая ось эллипса (перпендикулярна большей оси эллипса и проходит через ее центр)
a — большая полуось эллипса
b — малая полуось эллипса
O — центр эллипса (точка пересечения большей и малой осей эллипса)
Вершины эллипсa A1, A2, B1, B2 — точки пересечения эллипсa с малой и большой осями эллипсa
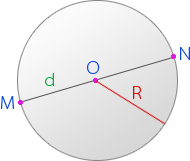
Диаметр эллипсa — отрезок, соединяющий две точки эллипса и проходящий через его центр.
Фокальное расстояние c — половина длины отрезка, соединяющего фокусы эллипсa.
Эксцентриситет эллипсa e характеризует его растяженность и определяется отношением фокального расстояния c к большой полуоси a. Для эллипсa эксцентриситет всегда будет 0 < e < 1, для круга e = 0, для параболы e = 1, для гиперболы e > 1.
Фокальные радиусы эллипсa r1, r2 — расстояния от точки на эллипсе до фокусов.
Радиус эллипсa R — отрезок, соединяющий центр эллипсa О с точкой на эллипсе.
| R = | ab | = | b |
| √a2sin2φ + b2cos2φ | √1 — e2cos2φ |
где e — эксцентриситет эллипсa, φ — угол между радиусом и большой осью A1A2.
Фокальный параметр эллипсa p — отрезок который выходит из фокуса эллипсa и перпендикулярный большой полуоси:
Коэффициент сжатия эллипсa (эллиптичность) k — отношение длины малой полуоси к большой полуоси. Так как малая полуось эллипсa всегда меньше большей, то k < 1, для круга k = 1:
k = √1 — e2
где e — эксцентриситет.
Сжатие эллипсa (1 — k ) — величина, которая равная разности между единицей и эллиптичностью:
Директрисы эллипсa — две прямые перпендикулярные фокальной оси эллипса, и пересекающие ее на расстоянии
ae
от центра эллипса. Расстояние от фокуса до директрисы равно
pe
.
Основные свойства эллипсa
1. Угол между касательной к эллипсу и фокальным радиусом r1 равен углу между касательной и фокальным радиусом r2 (Рис. 2, точка М3).
2. Уравнение касательной к эллипсу в точке М с координатами (xM, yM):
3. Если эллипс пересекается двумя параллельными прямыми, то отрезок, соединяющий середины отрезков образовавшихся при пересечении прямых и эллипса, всегда будет проходить через центр эллипсa. (Это свойство дает возможность построением с помощью циркуля и линейки получить центр эллипса.)
4. Эволютой эллипсa есть астероида, что растянута вдоль короткой оси.
5. Если вписать эллипс с фокусами F1 и F2 у треугольник ∆ ABC, то будет выполнятся следующее соотношение:
| 1 = | F1A ∙ F2A | + | F1B ∙ F2B | + | F1C ∙ F2C |
| CA ∙ AB | AB ∙ BC | BC ∙ CA |
Уравнение эллипсa
Каноническое уравнение эллипсa:
Уравнение описывает эллипс в декартовой системе координат. Если центр эллипсa О в начале системы координат, а большая ось лежит на абсциссе, то эллипсa описывается уравнением:
Если центр эллипсa О смещен в точку с координатами (xo, yo), то уравнение:
| 1 = | (x — xo)2 | + | (y — yo)2 |
| a2 | b2 |
Параметрическое уравнение эллипсa:
| { | x = a cos α | де 0 ≤ α < 2π |
| y = b sin α |
Радиус круга вписанного в эллипс
Круг, вписан в эллипс касается только двух вершин эллипсa B1 и B2. Соответственно, радиус вписанного круга r будет равен длине малой полуоси эллипсa OB1:
r = b
Радиус круга описанного вокруг эллипсa
Круг, описан вокруг эллипсa касается только двух вершин эллипсa A1 и A2. Соответственно, радиус описанного круга R будет равен длине большой полуоси эллипсa OA1:
R = a
Площадь эллипсa
Формула определение площади эллипсa:
S = πab
Площадь сегмента эллипсa
Формула площади сегмента, что находится по левую сторону от хорды с координатами (x, y) и (x, -y):
| S = | πab | — | b | ( | x | √ | a2 — x2 + a2 ∙ arcsin | x | ) |
| 2 | a | a |
Периметр эллипсa
Найти точную формулу периметра эллипсa L очень тяжело. Ниже приведена формула приблизительной длины периметра. Максимальная погрешность этой формулы ~0,63 %:
| L ≈ 4 | πab + (a — b)2 |
| a + b |
Длина дуги эллипсa
Формулы определения длины дуги эллипсa:
1. Параметрическая формула определения длины дуги эллипсa через большую a и малую b полуоси:
| t2 | ||
| l = | ∫ | √a2sin2t + b2cos2t dt |
| t1 |
2. Параметрическая формула определения длины дуги эллипсa через большую полуось a и эксцентриситет e:
| t2 | ||
| l = | ∫ | √1 — e2cos2t dt, e < 1 |
| t1 |
Перейти к содержанию
Длина эллипса (овала)
На чтение 1 мин
Эллипс – это множество точек плоскости, для которых сумма расстояний до фокусов эллипса постоянна и больше расстояния между фокусами.
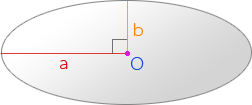
О – центр эллипса
Длина эллипса (L) равна произведению суммы его полуосей (a, b) на число π:
Вам также может понравиться
Дуга – это часть окружности, отсекаемая хордой.
0145
Окружность – геометрическое место точек, равноудаленных
0123
Окружность – геометрическое место точек, равноудаленных
0123
Многоугольник – это геометрическая фигура, которая
0141
Шестиугольник – это многоугольник, который имеет шесть углов.
0440
Пятиугольник – это многоугольник, который имеет пять углов.
0346
Трапеция – это четырехугольник, у которого параллельна
087
Квадрат – это параллелограмм, у которого все углы и
090