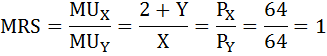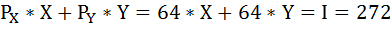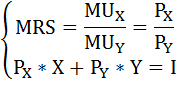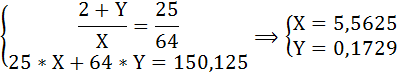Как найти размер потоварного налога

Патентная система налогообложения отличается от других режимов тем, что для расчёта налога учитывается не реальный, а потенциально возможный доход ИП.

Например, региональные власти одной области могут установить, что годовой доход парикмахера, подлежащий налогообложению, составляет 350 000 рублей, а в другом субъекте РФ это значение составляет 900 000 рублей. В результате стоимость патента по одному виду деятельности, но в разных российских регионах, может отличаться в несколько раз.

Кроме того, на территории самого региона выделяют муниципальные образования с разными значениями потенциально возможного дохода. Из-за этого патент в областном центре или крупном городе может стоить дороже, чем в небольшом населённом пункте.

С учётом этого, самостоятельный расчёт стоимости патента, а значит, и налоговой нагрузки, довольно сложен. Поэтому для ИП, которые хотят заранее знать, сколько надо будет платить, ФНС разработала специальный калькулятор патента.

Какие данные надо собрать перед расчётом

Перед тем, как рассчитать патент, соберите следующие данные:

• год, в котором будет действовать патент;
• день начала и окончания действия патента, с учётом того, что этот период составляет от 1 до 12 месяцев, в том числе неполных, в течение календарного года;
• УФНС, то есть субъект РФ;
• муниципальное образование, на территории которого ИП будет вести бизнес;
• вид деятельности, установленный региональным законом о ПСН.

Дополнительно может понадобиться физический показатель для некоторых направлений бизнеса:

• количество работников в патентной деятельности с учётом ограничения в 15 человек;
• грузоподъемность или количество транспортных средств;
• площадь или количество объектов недвижимости и др.

Примеры расчёта стоимости патента на калькуляторе ФНС

Покажем на конкретных примерах, как рассчитать патент на онлайн-калькуляторе ФНС.

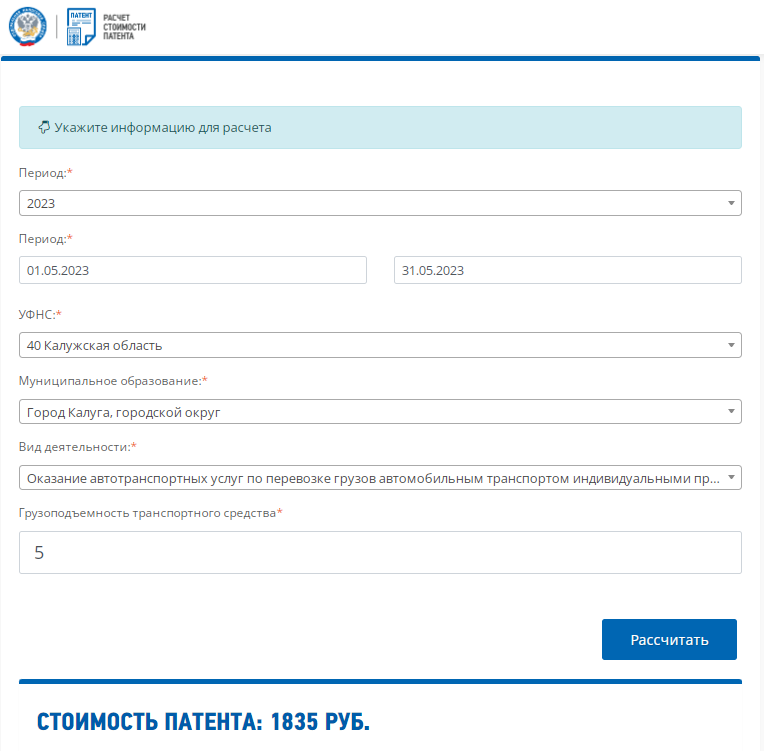
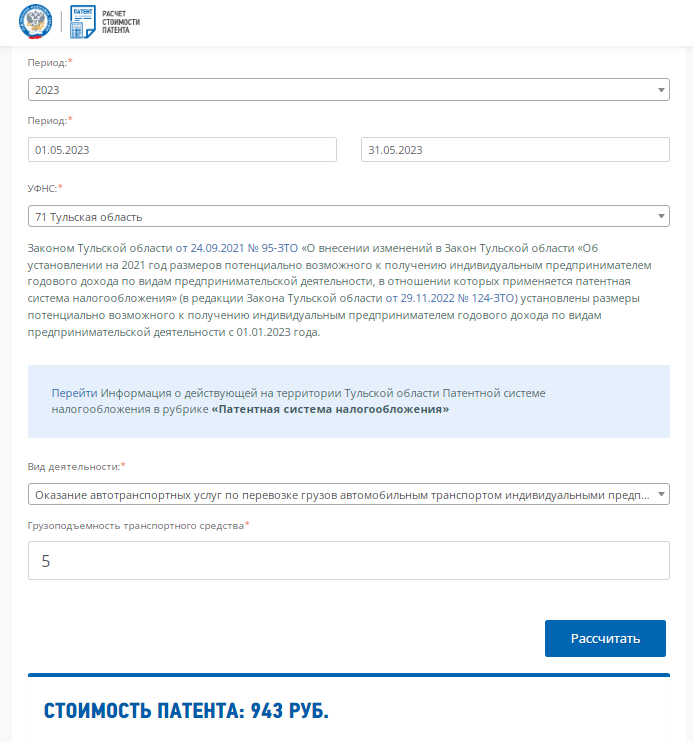
Пример 1: индивидуальный предприниматель без работников планирует заняться грузоперевозками на принадлежащем ему автомобиле грузоподъемностью 5 тонн. ИП проживает на границе Калужской и Тульской областей, поэтому хочет сравнить стоимость патента в обоих регионах. Для примера посчитаем налог на май 2023 года.

Поэтапно вводим нужные данные и нажимаем кнопку «Рассчитать».

Получаем, что за 31 день действия патента, выданного для Калуги, надо будет заплатить 1 835 рублей. Если же патент оформить в Тульской области, то его стоимость ниже – 943 рубля.

Казалось бы, очевидно, что выгоднее получать патент в Тульской области, ведь его стоимость почти в 2 раза меньше.

Однако калькулятор патента ФНС не учитывает, что налог можно уменьшить за счёт страховых взносов, которые ИП платит за себя и работников. В 2023 году минимальная сумма взносов за себя составляет 45 842 рубля.

Стоимость патента на весь 2023 год в Калуге равна 21 600 рублей, а в Тульской области — 11 100 рублей. В обоих случаях эта сумма меньше, чем страховые взносы, которые ИП перечисляет за себя. Учитывая, что у этого предпринимателя нет работников, налог на ПСН уменьшается без ограничений. А значит, платить за патент не придётся в обоих случаях.

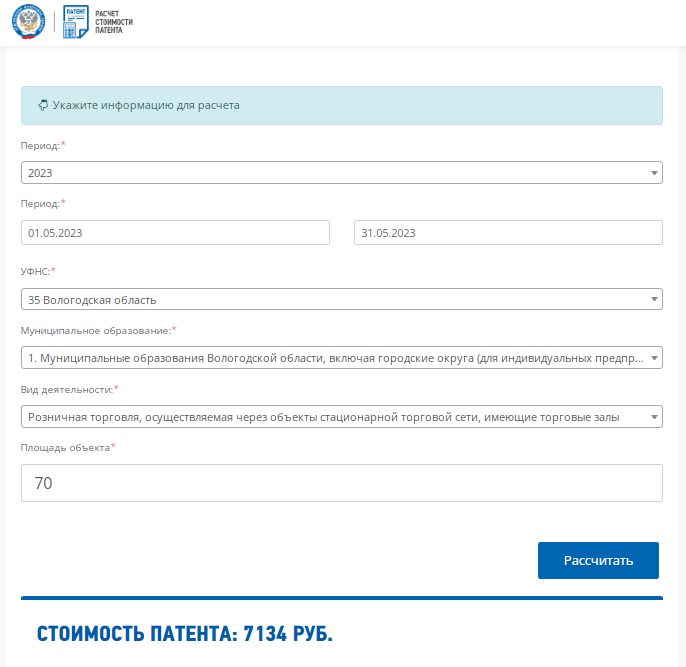
Пример 2: ИП с работниками открывает в Вологде розничный магазин на площади 70 кв. метров. Сделаем расчёт патента:

• на 31 день – 7 134 рублей;
• на весь 2023 год – 84 000 рублей.

Поскольку у предпринимателя есть наёмные работники, то он может уменьшить налог на сумму перечисленных страховых взносов, но с ограничением в 50%. Это означает, что стоимость патента для него составит 42 000 рублей за полный 2023 год.

Для более сложных случаев расчёта патента, например, для нескольких видов деятельности или в разных регионах, рекомендуем обращаться в ИФНС. А для наших пользователей мы можем предложить бесплатную налоговую консультацию по расчёту стоимости патента.

Бесплатная консультация по налогообложению

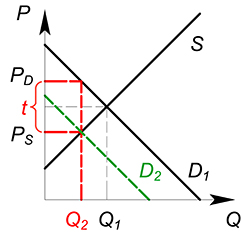
Потоварный налог — налог, представляющий собой фиксированную сумму, взимаемую с единицы продукции.

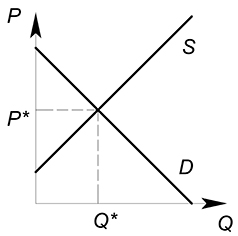
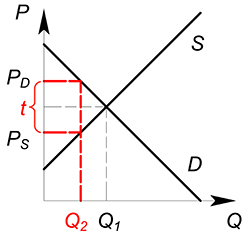
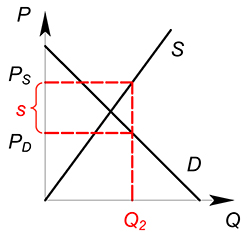
Рассмотрим некий рынок (возьмем для примера совершенно конкурентный). Раньше, до вмешательства государства, на данном рынке продавалось некоторое количество продукции $Q^*$ по цене $P^*$. Сумму, которую потребители уплачивали за единицу продукции, полностью получали производители. Цена покупки $P_D$ была равна цене продажи $P_S$.

Представим, что государство ввело на данном рынке потоварный налог по ставке $t$. Теперь фирма должна, получив от покупателя сумму $P_D$ за единицу продукции, отдать государству часть этой суммы, равную ставке налога $t$. В новых условиях фирма получает сумму $P_D-t$ за единицу товара. Фактически для фирмы уменьшилась цена, по которой она продает свой продукт. $P_S=P_D-t$. При введении налога количество покупаемого и продаваемого товара уменьшается.

Действие, которое оказывает налог на ситуацию на рынке, эквивалентно снижению спроса или увеличению издержек. Налог, наложенный на покупателя, окажет такое же влияние на рынок, что и налог, наложенный на производителя.

Рассмотрим, какое действие оказывает налог на функции издержек одной фирмы:

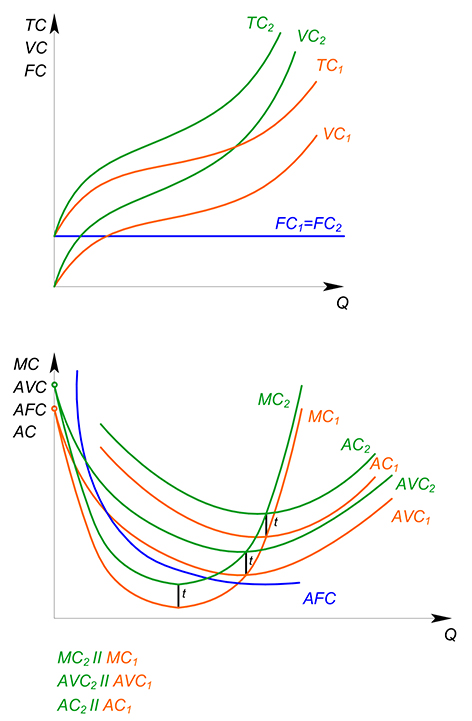
$TC(Q)_2=TC(Q)_1+tQ$

Пример 1
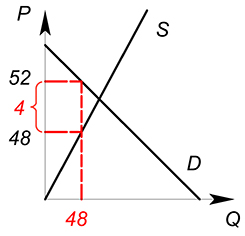
Спрос на совершенно конкурентном рынке задан функцией $Q_D=100-P_D$, предложение — $Q_S=P_S$, государство вводит налог по ставке 4, найти равновесное количество продаваемого товара, цену покупателя ($P_D$), цену продавца ($P_S$).

Решать такую задачу удобно, составив следующую систему уравнений:

$begin {cases}
Q_D=100-P_D\
Q_S=P_S\
Q_D=Q_S\
P_D=P_S+4
end {cases}$

Отсюда получаем:

$100-(P_S+4)=P_S$

$P_S=48$

$P_D=48+4=52$

$Q_D=Q_S=48$

Пример 2
Спрос на совершенно конкурентном рынке задан функцией $Q_D=100-P_D$, предложение — $Q_S=P_S$, государство хочет максимизировать сумму налоговых поступлений. Найдите $Q^*$, $P_D$, $P_S$, оптимальную ставку налога, сумму налоговых поступлений, построить кривую Лаффера

$begin {cases}
Q_D=100-P_D\
Q_S=P_S\
Q_D=Q_S\
P_D=P_S+t
end {cases}$

$100-P_S-t=P_S$

$P_S=dfrac{100-t}{2}$

$Q_S=P_S=dfrac{100-t}{2}$

Сумма налоговых поступлений будет равна ставке налога, умноженной на количество проданного товара:

$T=tcdot Q^*$

$T(t)=tcdot Q(t)$

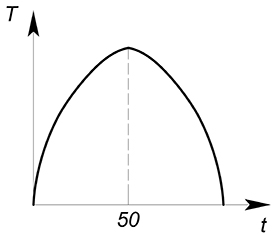
$T(t)=tcdot (dfrac{100-t}{2})=50t-0{,}5t^2$

Данная функция, описывающая зависимость суммы налоговых поступлений от ставки налога, называется кривой Лаффера.

Максимизируем данную функцию:

$T'(t)=50-t$

$t^*=50$

$T»(t)=-1<0$, максимум

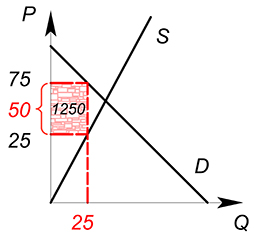
Теперь изобразим ее:

$Q_D=Q_S=25$

$P_D=75$

$P_S=25$

$T=50cdot 25=1250$

Пример 3

Принцип введения налога на монополизированном рынке такой же как и на совершенно конкурентном.

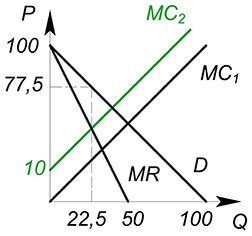
$P_D(Q)=100-Q$, $TC(Q)=Q^2+10$, $t=510$, найти прибыль фирмы после введения налога

Введем налог на продавца. Он увеличивает издержки фирмы:

$TC(Q)_2=TC(Q)_1+tQ=Q^2+10Q+10$

$pi(Q)=100Q-Q^2-Q^2-10Q-10=90Q-2Q^2-10$

$pi'(Q)=90-4Q=0$

$Q^*=22{,}5$

$pi(Q)=1002{,}5>0$, фирма остается на рынке

Пример 4

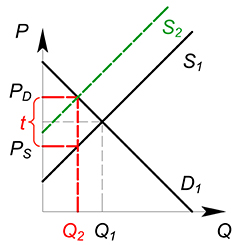
Действие потоварной субсидии обратно действию потоварного налога.

Спрос на совершенно конкурентном рынке задан функцией $Q_D=100-P_D$, предложение — $Q_S=P_S$, государство вводит субсидию по ставке 4, найти равновесное количество продаваемого товара, цену покупателя ($P_D$), цену продавца ($P_S$).

Покупатель платит за единицу товара $P_D$ меньшую $P_S=P_D+s$

$begin {cases}
Q_D=100-P_D\
Q_S=P_S\
Q_D=Q_S\
P_D=P_S-4
end {cases}$

$100-P_S+s=P_S$

$P_S=52$

$P_D=48$

$Q_S=Q_D=52$

Предпочтения потребителя описываются функцией полезности

U = 2×X + X×Y.

Пусть P_x = 25, P_y = 64, а доход потребителя равен 272.

Правительство рассматривает два варианта налогообложения:

1) ввести потоварный налог на х в размере 39 ден. ед.

2) ввести аккордный налог на потребителей, который обеспечил бы ту же налоговую выручку.

Определите, какой из вариантов предпочтителен с точки зрения благосостояния потребителей после налогообложения.

Решение:

1) Введение потоварного налога повышает цену на благо х для потребителя на 39 ден. ед.:

P_X = 25 + 39 = 64 ден. ед.

Государство получит 39 ден. ед. с каждой единицы блага Х.

Чтобы определить общий размер отчислений потребителя в государственный бюджет, найдём оптимальный объём потребления блага X, воспользовавшись условием максимизации полезности потребителя при данном бюджетном ограничении – равенством предельной нормы замещения блага Х благом Y отношению цен товаров.

(Как определить предельную полезность было рассмотрено в задаче №64)

Уравнение бюджетного ограничения:

Отсюда X = 3,125, а Y = 1,125.

Уровень полезности, которого достигает потребитель:

U₁ = 2 × 3,125 + 3,125 × 1,125 = 9,77

Следовательно, государство получает в виде сбора:

3,125 × 39 = 121,875 ден. ед.

2) Если бы был введён аккордный налог равный 121,875, бюджет потребителя сократился бы до 150,125:

272 – 121,875 = 150,125

Оптимальный объём благ Х и Y удовлетворял бы условиям:

Уровень полезности, которого достигает потребитель:

U₂ = 2 × 5,5625 + 5,5625 × 0,1729 = 12,09.

Можно сделать вывод, что аккордный налог предпочтительнее, поскольку при том же объёме налоговых отчислений в пользу государства он позволяет потребителю достичь более высокого уровня полезности:

U₂ ˃ U₁.

Лекция: налогообложение

В результате
введения налогов и субсидий появляются
стимулы для увеличения
(уменьшения) производства и /или
потребления.

Рассмотрим влияние
различных видов налогов на рыночное
равновесие.

Аккордный
(паушальный) —
налог, взимаемый в виде фиксированной
суммы (Тх=соnst).
Пример — плата за лицензию.

Количественный
— налог,
сумма которого зависит от размера
налогооблагаемой базы (стоимостной,
физической или иной характеристики
объекта налогообложения). Внутри данной
группы налогов нас будут интересовать
два вида: потоварный и стоимостной.

Потоварный —
налог, сумма которого зависит от размера
выпуска. Налоговая ставка (t)
указывает, какая сумма должна быть
уплачена государству с каждой единицы
объема продаж. Общая сумма налоговых
сборов равна: Тх
= tQ. Пример —
специфические акцизы (акцизы с твердыми
налоговыми ставками в виде абсолютной
суммы на единицу измерения, например,
акцизы на спиртосодержащую продукцию,
бензин и автомобили в России).

Стоимостной
— налог, сумма которого зависит от
стоимости реализации. Налоговая ставка
(t) указывает, какая доля стоимости
реализации должна быть уплачена
государству в виде налога.

Общая сумма налоговых
сборов равна: Тх
= t∙[РQ].
Однако данное выражение может быть
записано в другом виде: Тх=[tР]∙Q.
В этом_случае налоговую ставку (t)
можно интерпретировать как долю цены
реализации, которая должна быть уплачена
государству виде налога с каждой
проданной единицы товара.

Внутри данной
группы налога также выделяют два вида
в зависимости от того, цена потребителя
(Рd) или производителя (Рs)
используется при расчете стоимости
реализации. Примером первого варианта
могут служить адвалорные акцизы, второго
— НДС и налог с продаж.

Рассмотрим более
подробно последствия применения
потоварного налога, НДС и адвалорного
акциза. Прежде всего, остановимся на
общих положениях, касающихся всех видов
рассматриваемых налогов.

Во-первых, все они
приводят к тому, что после налогообложения
цена,
уплачиваемая за товар потребителем,
оказывается выше цены, которую получает
производитель.
Действительно, если налог платит
производитель, то после расчета с
покупателем он должен часть цены товара
перечислить в виде налога государству,
то есть продавец получит меньше, чем
заплатил потребитель.

Если же налог
оплачивает покупатель, то после расчета
с продавцом, он обязан еще некоторую
сумму перечислить в виде налога, в итоге
заплатив больше, чем получил производитель.
Различия же трех видов налогов касаются
только того, на сколько отличаются
указанные величины.

Последствия применения потоварного налога

Пусть первоначально
рынок товара находится в равновесии.
Если первоначальная кривая спроса имела
вид:

,
а кривая предложения:

,
то в таком случае равновесие до применения
налога соответствовало решению следующей
системы уравнений:

.

(1)

На графике равновесие
установится в точке пересечения кривых
спроса и предложения —
.
Равновесный объем составит

единиц товара, а равновесная цена —
.

Пусть правительство
установило налог (per
unit
tax)
в виде фиксированной суммы t
(ден.ед.),
отчисляемой с каждой единицы товара.
Введение потоварного налога приводит
к одинаковому результату независимо
от того, кто непосредственно платит
налог в государственный бюджет —
потребители или производители товара.

Если потоварный
налог уплачивают производители,
то издержки производства каждой единицы
продукции возрастут на величину
потоварного налога. Предложение товара
уменьшится, кривая предложения сдвинется
из положения

в положение

(рис.1). Расстояние по вертикали между
кривыми предложения

и

равно потоварному налогу t
при любом объеме выпуска.

Рис.1

Потребители покупают
товар по цене

=
(цена
потребителя), из которой производители
уплачивают налог t
за каждую единицу проданного товара.
Фактическая цена, которую получают
производители (фирмы) за каждую единицу
товара, равна Рs
= Рd
– t. По цене Рs
производители поставят на рынок товар
в объеме единиц

.

После применения
налога (независимо от того, на продавца
или потребителя он был наложен) возникает
другая система уравнений:

(2)

Подставим в уравнение
1 системы (2)

,
и приравняем

,
получим:

(3)

Приравняв уравнения
системы, получим: a-b
или

;

Подставив «цену
потребителя» в уравнение 1 системы (2),
определим равновесный объем продаж
после введения налога

,
а вычитая из

налог t, получим «цену производителя»-
Ps.

Упражнение 1.

Предложение
авторучек в селе Замараево задается
функцией
,
а спрос на них

( количество,
штук, P — цена, рублей). Государство вводит
налог, уплачиваемый продавцами, в размере
10 рублей на каждую проданную авторучку.

Определите:

• объем продаж и
  цену авторучки до и после введения
  налога;

• чему будут равны
  налоговые поступления в бюджет, и как
  налоговое бремя распределится между
  покупателями и продавцами;

• как изменятся
  излишки покупателей и продавцов после
  введения налога;

• чему равна
  величина безвозвратных потерь?

Решение:

1. Определим
   первоначальные параметры равновесия.
   Приравняем функцию спроса к функции
   предложения и определим равновесную
   цену, учитывая, что в точке равновесия
   Pd=Ps=P.
   
   .
   
   =70;
   Q₁=150.

2. Излишки потребителей
   до введения налога: CS_{1=
   .}

3. Излишки
   производителя до введения налога:
   PS₁=
   

4. Новая (после
   введения налога) функция предложения
   будет иметь вид:

=3(Р-10)-60=3Р-90.

5. Равновесные
цена и объем продаж после введения
налога составят:

360-3Р = 3P
-90. 450 = 6P.



= 75 (д.е.).Q₂
= 135(шт.).

=P_d—
это «цена потребителя», производитель,
после уплаты налога получит цену

6. Доходы
государственного бюджета от введения
налога составят: Т= Q₂∙t₌1350
д.е.

7. Налоговое бремя
на потребителей Tc=
=(75-70)∙135=5∙135=675.

8. Налоговое бремя
на производителей T_Р=1350-675=675.

9. Излишки
потребителя после введения налога:
CS_2=
.

10. Излишки
производителя после введения налога:
PS_2=
.

11. Чистые потери
общества от введения налога DWL=

Рассмотрим вариант,
соответствующий введению потоварного
налога на потребителей. В этом случае
потребители снизят свой спрос на товар,
и кривая спроса сдвинется вниз вдоль
оси Р на величину налога t. Иными словами,
потребители будут готовы приобрести
такое же, как и прежде, количество товара
только по цене на t ден.ед. ниже
первоначальной.

Подставим в уравнение
1 системы (2)

,
и приравняем

получим

a-b(
)=
.Определим
цену , которую получит производитель
после уплаты налога на производителя:

.

«Цена потребителя»

.

Подставив «цену
потребителя» в уравнение 1 системы (2)
или «цену производителя» в уравнение
2 системы (2), определим равновесный
объем продаж после введения налога.

Упражнение 2.

Функции спроса
и предложения на рынке товара Х описываются
уравнениями

,

.
Государство вводит фиксированный сбор,
взимаемый с покупателя в 5 ден.ед.

Определите:

• объем продаж и
  цену товара Х до и после введения налога;
  

• чему будут равны
  налоговые поступления в бюджет, и как
  налоговое бремя распределится между
  покупателями и продавцами;

• как изменятся
  излишки покупателей и продавцов после
  введения налога;

• чему равна
  величина безвозвратных потерь?

Решение:

1. Определим
   первоначальные параметры равновесия.
   Приравняем функцию спроса к функции
   предложения и определим равновесную
   цену, учитывая, что в точке равновесия
   Pd=Ps=P.

.

=7;
Q₁=23.

1. Излишки потребителей
   до введения налога составляли: CS_{1=
   .}

2. Излишки
   производителя до введения налога
   составляли: PS₁=
   

3. Новая (после
   введения налога) функция спроса будет
   иметь вид:

=30-(Рs+5)=25-Ps.

1. Равновесные цена
   и объем продаж после введения налога
   составят:

,

=Ps
= 6 (ден.ед.). Q₂
= 19 ед. Новая равновесная цена

=P_s—
это «цена производителя», потребитель,
после уплаты налога получит цену

1. Доходы
   государственного бюджета от введения
   налога составят: Т= Q₂∙t₌19∙5=95
   ден.ед.

2. Налоговое бремя
   на потребителей (площадь прямоугольника
   
   
   )
   составит Tc=
   =(11-7)∙19=4∙19=76
   ден.ед.

3. Налоговое бремя
   на производителей (площадь прямоугольника
   
   
   )
   составит

T_Р=95-76=19
ден.ед.

1. Излишки потребителей
   после введения налога: CS_{2=
   .}

2. Излишки
   производителей после введения налога:
   PS_{2=
   .}

3. Чистые потери
   общества от введения налога DWL=
   

В результате
введения потоварного налога:

• сократится
  равновесный объем товара, реализуемого
  на рынке,

• повысится рыночная
  цена товара, Р_d
  > Р₁;

• потребители получат
  меньше товара и по более высокой цене;

• производители
  смогут реализовать меньший объем товара
  и по более низкой цене.

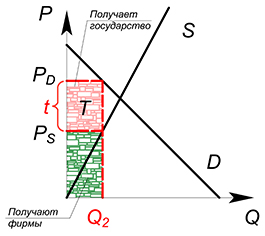
Общая сумма налога
Т, поступающего в бюджет, равна Т=t∙
.
Хотя налог непосредственно платят
продавцы, фактически он распределяется
между покупателями и продавцами:
потребители платят налог

=
,
производители – налог

.
Распределение общей суммы налога Т
между покупателями и продавцами зависит
от эластичности спроса и предложения.

Чем более
эластичен спрос, тем меньшую часть
налога при прочих равных условиях
выплачивают потребители и большую часть
– производители. Чем более эластично
предложение, тем меньшую часть налога
при прочих равных условиях выплачивают
производители и большую часть потребители.

От введения
потоварного налога проиграют и
потребители, и производители. На рынке
данного товара проиграет общество в
целом, так как излишки потребителей и
производителей уменьшатся не только
на величину налоговых поступлений в
бюджет, но и на величину безвозвратных
потерь DWL.
Из производства данного товара ресурсы
перераспределяются в другие отрасли,
что вызовет в них искажения цен и объемов.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #