Разложение Бинома Ньютона
Онлайн калькулятор разложения степени Бинома
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone — просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android — просто добавьте страницу
«На главный экран»

как решить (√2+2)^2 ?
- reply
Корень из двух на два будет просто два, и два на два 4 в итоге будет 6
- reply
Чему равен коэффициент пятого члена разложения бинома (2x+3)^9 ?
- reply
как решить (x+а)^5?
- reply
х^5+5а*х^4+10а^2*х^3+10а^3*х^2+5а^4*х+а^5
- reply
|
3 / 3 / 0 Регистрация: 18.05.2012 Сообщений: 150 |
|
|
1 |
|
Найти номер члена разложения бинома, который не содержит х26.03.2013, 23:30. Показов 14088. Ответов 3
( Если можно,с комментариями)Спасибо!
0 |
|
Programming Эксперт 94731 / 64177 / 26122 Регистрация: 12.04.2006 Сообщений: 116,782 |
26.03.2013, 23:30 |
|
Ответы с готовыми решениями: Используя формулу бинома Ньютона, найти член разложения бинома 9. Используя формулу бинома Ньютона, найти член разложения… Найти номер первого члена последовательности, который отличается от предыдущего члена не более чем на заданное значение Найти члены разложения бинома Найти рациональные члены разложения бинома 3 |
|
4216 / 3411 / 396 Регистрация: 15.06.2009 Сообщений: 5,818 |
|
|
27.03.2013, 00:30 |
2 |
|
Бином Ньютона: (a+b)n=? P.S. Переводить с украинского нужно всё-таки грамотно: розкладання (укр) = разложение, а не розклад = расписание (онлайн-переводчики — зло без знания языка).
0 |
|
2 / 1 / 1 Регистрация: 29.12.2017 Сообщений: 6 |
|
|
11.03.2018, 09:20 |
3 |
|
думаю тут больше нечего объяснять.
0 |
|
3971 / 2950 / 894 Регистрация: 19.11.2012 Сообщений: 6,063 |
|
|
11.03.2018, 18:37 |
4 |
|
думаю тут больше нечего объяснять. Ну да — всего-то неполных пять лет потребовалось.
0 |
Урок № 13 по алгебре и н.м.а в 10 классе 30.09.20г
Учитель Евтушенко М.С.
Общая тема: Рациональные уравнения и неравенства
Тема: Решение упражнений
Тип урока: закрепление изученного материала
Планируемые результаты:
Личностные:
Развивать готовность к самообразованию и решению задач;
Метапредметные:
Учиться критично относиться к своему мнению, с достоинством признавать свои ошибки;
Предметные: научатся самостоятельно находить члены бинома Ньютона.
Формы работы: фронтальная, индивидуальная
Образовательные ресурсы: карточки
ХОД УРОКА
-
Организационный момент. Проверка домашнего задания.
-
Постановка цели и задач урока. Мотивация.
3 . Практическая работа .Бином Ньютона
Вопросы к работе
-
Прочитать формулу бинома Ньютона.
-
Как строится треугольник Паскаля для нахождения коэффициентов бинома Ньютона?
-
По какой формуле найти s-й член бинома Ньютона?
Образцы решения заданий
Пример 1. Написать разложение по формуле бинома Ньютона и упростить .
Решение:
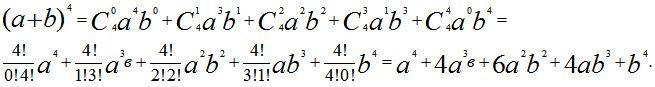
Пример 2. Найти алгебраическую сумму коэффициентов многочлена относительно x, получаемого в разложении бинома Ньютона .
Решение.
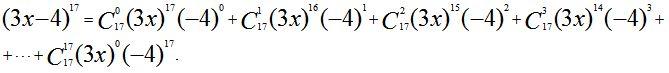
Это равенство истинно при любом значении х.
При x = 1 левая часть равна , а в правой части получаем алгебраическую сумму коэффициентов:
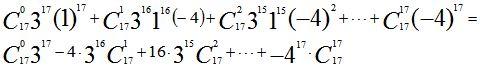
Следовательно, алгебраическая сумма коэффициентов данного многочлена равна –1.
Пример 3. Найти 13-й член разложения бинома
.
Решение. Согласно формуле общего члена разложения бинома,
Пример 4. Найти номер члена разложения бинома , не содержащего х.
Решение. Для общего члена разложения имеем 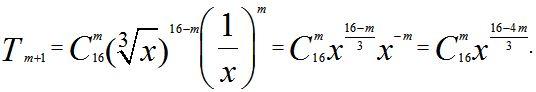
Член разложения не зависит от x; это значит, что показатель степени x равен 0, только тогда, когда , 16 – 4m = 0, m = 4.
Итак, пятый член данного разложения не зависит от х.
Пример 5. Построить треугольник Паскаля для нахождения
коэффициентов разложения бинома Ньютона .
Решение.
|
n |
|
|
0 |
1 |
|
1 |
1 1 |
|
2 |
1 2 1 |
|
3 |
1 3 3 1 |
|
4 |
1 4 6 4 1 |
|
5 |
1 5 10 10 5 1 |
|
6 |
1 6 15 20 15 6 1 |
|
7 |
1 7 21 35 35 21 7 1 |
|
|
Упражнения
-
Написать разложение по формуле бинома Ньютона и упростить:
а) ; Ответ:
.
б) ; Ответ:
.
в) ; Ответ: .
2. Найти пятый и девятый член разложения:
а) , б) . Ответ: .
3. Найти два средних члена разложения . Ответ: .
4. Найти в биномиальном разложении член, не содержащий z. (Ответ: ).
5. Используя треугольник Паскаля найти коэффициенты разложения:
а) , .
Индивидуальные задания
-
Разложить по формуле бинома Ньютона и упростить. Коэффициенты разложения найти, используя треугольник Паскаля:
1) ; 2) ; 3) ;
4) ; 5) ; 6) ;
7) ; 
10)
2. Найти два средних члена разложения:
1) ; 2) ; 3) ; 4) ;
Итоги урока. Рефлексия
Домашнее задание: решить № 2.21(а,в)
Название биномиальных коэффициентов следует из теоремы, известной в математике как Формула Бинома Ньютона.
Теорема 11.1. 
Теорема 11.2. 
Доказательство. По формуле бинома с использованием тождественных преобразований алгебраических выражений.
.■
Последнее равенство также называется формулой бинома Ньютона, его правая часть называется разложением степени бинома.
Теорема 11.3.
Доказательство следует из формулы бинома Ньютона при
Теорема 11.4.
Доказательство следует из формулы бинома Ньютона при .
Формулы сокращённого умножения являются частными случаями формулы бинома Ньютона.
1) квадрат суммы при :

Заменив в формуле квадрата суммы B на (–B), получаем формулу квадрата разности:
2) куб суммы при :

Задачи и упражнения.
11.1. Найдите разложение бинома.
11.2. Найдите член разложения бинома 
11.3. Найдите наибольший коэффициент разложения бинома , если сумма всех коэффициентов равна 4096.
11.4. Найдите Х в 
.
11.5. Докажите, что сумма квадратов коэффициентов разложения бинома равна
.
12. Треугольник Паскаля.
Для вычисления биномиальных коэффициентов используется специальная таблица.
Таблица 2
Вычисление биномиальных коэффициентов
Биномиальные коэффициенты удобно выстроить в Треугольник Паскаля – равнобедренный треугольник, обладающий следующими закономерностями:
1) в строке треугольника записываются биномиальные коэффициенты
-й степени бинома;
2) число располагается в
строке на
месте;
3) боковые стороны треугольника состоят только из единиц;
4) каждое внутреннее число строки равно сумме двух последовательных чисел предыдущей строки, стоящих над ним слева и справа.
На рисунке 7 представлен треугольник Паскаля, выстроенный для коэффициентов разложения бинома -й степени.
Рис. 1
Треугольник Паскаля
Например, при треугольник Паскаля имеет вид:
Значит, .
Задачи и упражнения.
12.1. Найдите разложение бинома.
12.2. Докажите, что .
12.3. Проверьте выполнение равенства задачи 3.27 для 8 и 10 строк треугольника Паскаля.
| < Предыдущая | Следующая > |
|---|








