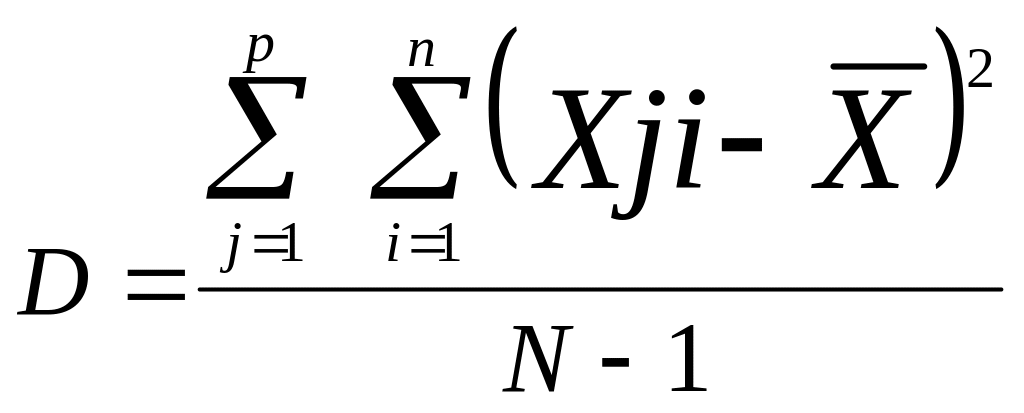Из предыдущей статьи мы узнали о таких показателях, как размах вариации, межквартильный размах и среднее линейное отклонение. В этой статье изучим дисперсию, среднеквадратичное отклонение и коэффициент вариации.
Дисперсия
Дисперсия случайной величины – это один из основных показателей в статистике. Он отражает меру разброса данных вокруг средней арифметической.
Сейчас небольшой экскурс в теорию вероятностей, которая лежит в основе математической статистики. Как и матожидание, дисперсия является важной характеристикой случайной величины. Если матожидание отражает центр случайной величины, то дисперсия дает характеристику разброса данных вокруг центра.
Формула дисперсии в теории вероятностей имеет вид:
То есть дисперсия — это математическое ожидание отклонений от математического ожидания.
На практике при анализе выборок математическое ожидание, как правило, не известно. Поэтому вместо него используют оценку – среднее арифметическое. Расчет дисперсии производят по формуле:
где
s2 – выборочная дисперсия, рассчитанная по данным наблюдений,
X – отдельные значения,
X̅– среднее арифметическое по выборке.
Стоит отметить, что у такого расчета дисперсии есть недостаток – она получается смещенной, т.е. ее математическое ожидание не равно истинному значению дисперсии. Подробней об этом здесь. Однако при увеличении объема выборки она все-таки приближается к своему теоретическому аналогу, т.е. является асимптотически не смещенной.
Простыми словами дисперсия – это средний квадрат отклонений. То есть вначале рассчитывается среднее значение, затем берется разница между каждым исходным и средним значением, возводится в квадрат, складывается и затем делится на количество значений в данной совокупности. Разница между отдельным значением и средней отражает меру отклонения. В квадрат возводится для того, чтобы все отклонения стали исключительно положительными числами и чтобы избежать взаимоуничтожения положительных и отрицательных отклонений при их суммировании. Затем, имея квадраты отклонений, просто рассчитываем среднюю арифметическую. Средний – квадрат – отклонений. Отклонения возводятся в квадрат, и считается средняя. Теперь вы знаете, как найти дисперсию.
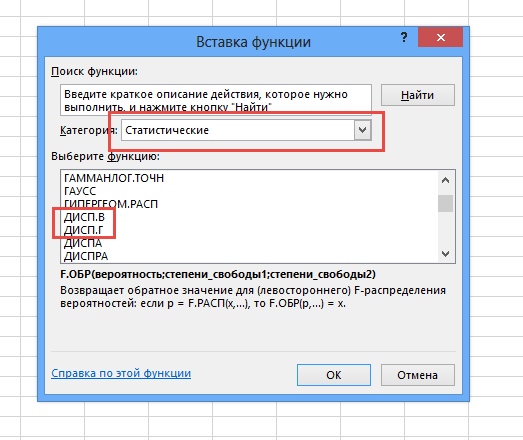
Генеральную и выборочную дисперсии легко рассчитать в Excel. Есть специальные функции: ДИСП.Г и ДИСП.В соответственно.
В чистом виде дисперсия не используется. Это вспомогательный показатель, который нужен в других расчетах. Например, в проверке статистических гипотез или расчете коэффициентов корреляции. Отсюда неплохо бы знать математические свойства дисперсии.
Свойства дисперсии
Свойство 1. Дисперсия постоянной величины A равна 0 (нулю).
D(A) = 0
Свойство 2. Если случайную величину умножить на постоянную А, то дисперсия этой случайной величины увеличится в А2 раз. Другими словами, постоянный множитель можно вынести за знак дисперсии, возведя его в квадрат.
D(AX) = А2 D(X)
Свойство 3. Если к случайной величине добавить (или отнять) постоянную А, то дисперсия останется неизменной.
D(A + X) = D(X)
Свойство 4. Если случайные величины X и Y независимы, то дисперсия их суммы равна сумме их дисперсий.
D(X+Y) = D(X) + D(Y)
Свойство 5. Если случайные величины X и Y независимы, то дисперсия их разницы также равна сумме дисперсий.
D(X-Y) = D(X) + D(Y)
Среднеквадратичное (стандартное) отклонение
Если из дисперсии извлечь квадратный корень, получится среднеквадратичное (стандартное) отклонение (сокращенно СКО). Встречается название среднее квадратичное отклонение и сигма (от названия греческой буквы). Общая формула стандартного отклонения в математике следующая:
На практике формула стандартного отклонения следующая:
Как и с дисперсией, есть и немного другой вариант расчета. Но с ростом выборки разница исчезает.
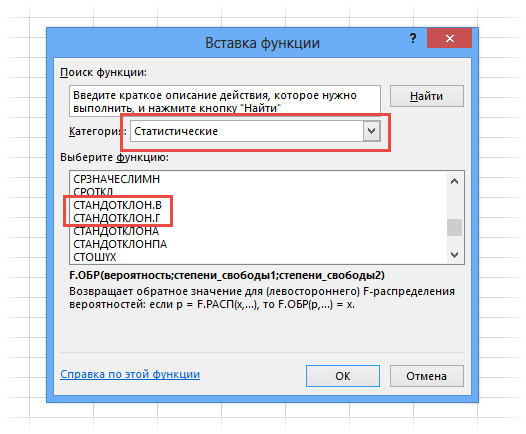
Расчет cреднеквадратичного (стандартного) отклонения в Excel
Для расчета стандартного отклонения достаточно из дисперсии извлечь квадратный корень. Но в Excel есть и готовые функции: СТАНДОТКЛОН.Г и СТАНДОТКЛОН.В (по генеральной и выборочной совокупности соответственно).
Среднеквадратичное отклонение имеет те же единицы измерения, что и анализируемый показатель, поэтому является сопоставимым с исходными данными.
Коэффициент вариации
Значение стандартного отклонения зависит от масштаба самих данных, что не позволяет сравнивать вариабельность разных выборках. Чтобы устранить влияние масштаба, необходимо рассчитать коэффициент вариации по формуле:
По нему можно сравнивать однородность явлений даже с разным масштабом данных. В статистике принято, что, если значение коэффициента вариации менее 33%, то совокупность считается однородной, если больше 33%, то – неоднородной. В реальности, если коэффициент вариации превышает 33%, то специально ничего делать по этому поводу не нужно. Это информация для общего представления. В общем коэффициент вариации используют для оценки относительного разброса данных в выборке.
Расчет коэффициента вариации в Excel
Расчет коэффициента вариации в Excel также производится делением стандартного отклонения на среднее арифметическое:
=СТАНДОТКЛОН.В()/СРЗНАЧ()
Коэффициент вариации обычно выражается в процентах, поэтому ячейке с формулой можно присвоить процентный формат:
Коэффициент осцилляции
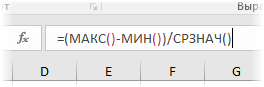
Еще один показатель разброса данных на сегодня – коэффициент осцилляции. Это соотношение размаха вариации (разницы между максимальным и минимальным значением) к средней. Готовой формулы Excel нет, поэтому придется скомпоновать три функции: МАКС, МИН, СРЗНАЧ.
Коэффициент осцилляции показывает степень размаха вариации относительно средней, что также можно использовать для сравнения различных наборов данных.
Таким образом, в статистическом анализе существует система показателей, отражающих разброс или однородность данных.
Ниже видео о том, как посчитать коэффициент вариации, дисперсию, стандартное (среднеквадратичное) отклонение и другие показатели вариации в Excel.
Поделиться в социальных сетях:
Стандартное отклонение (англ. Standard Deviation) — простыми словами это мера того, насколько разбросан набор данных.
Вычисляя его, можно узнать, являются ли числа близкими к среднему значению или далеки от него. Если точки данных находятся далеко от среднего значения, то в наборе данных имеется большое отклонение; таким образом, чем больше разброс данных, тем выше стандартное отклонение.
Стандартное отклонение обозначается буквой σ (греческая буква сигма).
Стандартное отклонение также называется:
- среднеквадратическое отклонение,
- среднее квадратическое отклонение,
- среднеквадратичное отклонение,
- квадратичное отклонение,
- стандартный разброс.
Использование и интерпретация величины среднеквадратического отклонения
Стандартное отклонение используется:
- в финансах в качестве меры волатильности,
- в социологии в опросах общественного мнения — оно помогает в расчёте погрешности.
Пример:
Рассмотрим два малых предприятия, у нас есть данные о запасе какого-то товара на их складах.
| День 1 | День 2 | День 3 | День 4 | |
|---|---|---|---|---|
| Пред.А | 19 | 21 | 19 | 21 |
| Пред.Б | 15 | 26 | 15 | 24 |
В обеих компаниях среднее количество товара составляет 20 единиц:
- А -> (19 + 21 + 19+ 21) / 4 = 20
- Б -> (15 + 26 + 15+ 24) / 4 = 20
Однако, глядя на цифры, можно заметить:
- в компании A количество товара всех четырёх дней очень близко находится к этому среднему значению 20 (колеблется лишь между 19 ед. и 21 ед.),
- в компании Б существует большая разница со средним количеством товара (колеблется между 15 ед. и 26 ед.).
Если рассчитать стандартное отклонение каждой компании, оно покажет, что
- стандартное отклонение компании A = 1,
- стандартное отклонение компании Б ≈ 5.
Стандартное отклонение показывает эту волатильность данных — то, с каким размахом они меняются; т.е. как сильно этот запас товара на складах компаний колеблется (поднимается и опускается).
Расчет среднеквадратичного (стандартного) отклонения
Формулы вычисления стандартного отклонения

σ — стандартное отклонение,
xi — величина отдельного значения выборки,
μ — среднее арифметическое выборки,
n — размер выборки.
Эта формула применяется, когда анализируются все значения выборки.

S — стандартное отклонение,
n — размер выборки,
xi — величина отдельного значения выборки,
xср — среднее арифметическое выборки.
Эта формула применяется, когда присутствует очень большой размер выборки, поэтому на анализ обычно берётся только её часть.
Единственная разница с предыдущей формулой: “n — 1” вместо “n”, и обозначение «xср» вместо «μ».
Разница между формулами S и σ («n» и «n–1»)
Состоит в том, что мы анализируем — всю выборку или только её часть:
- только её часть – используется формула S (с «n–1»),
- полностью все данные – используется формула σ (с «n»).
Как рассчитать стандартное отклонение?
Пример 1 (с σ)
Рассмотрим данные о запасе какого-то товара на складах Предприятия Б.
| День 1 | День 2 | День 3 | День 4 | |
| Пред.Б | 15 | 26 | 15 | 24 |
Если значений выборки немного (небольшое n, здесь он равен 4) и анализируются все значения, то применяется эта формула:
Применяем эти шаги:
1. Найти среднее арифметическое выборки:
μ = (15 + 26 + 15+ 24) / 4 = 20
2. От каждого значения выборки отнять среднее арифметическое:
x1 — μ = 15 — 20 = -5
x2 — μ = 26 — 20 = 6
x3 — μ = 15 — 20 = -5
x4 — μ = 24 — 20 = 4
3. Каждую полученную разницу возвести в квадрат:
(x1 — μ)² = (-5)² = 25
(x2 — μ)² = 6² = 36
(x3 — μ)² = (-5)² = 25
(x4 — μ)² = 4² = 16
4. Сделать сумму полученных значений:
Σ (xi — μ)² = 25 + 36+ 25+ 16 = 102
5. Поделить на размер выборки (т.е. на n):
(Σ (xi — μ)²)/n = 102 / 4 = 25,5
6. Найти квадратный корень:
√((Σ (xi — μ)²)/n) = √ 25,5 ≈ 5,0498
Пример 2 (с S)
Задача усложняется, когда существуют сотни, тысячи или даже миллионы данных. В этом случае берётся только часть этих данных и анализируется методом выборки.
У Андрея 20 яблонь, но он посчитал яблоки только на 6 из них.
Популяция — это все 20 яблонь, а выборка — 6 яблонь, это деревья, которые Андрей посчитал.
| Яблоня 1 | Яблоня 2 | Яблоня 3 | Яблоня 4 | Яблоня 5 | Яблоня 6 |
| 9 | 2 | 5 | 4 | 12 | 7 |
Так как мы используем только выборку в качестве оценки всей популяции, то нужно применить эту формулу:
Математически она отличается от предыдущей формулы только тем, что от n нужно будет вычесть 1. Формально нужно будет также вместо μ (среднее арифметическое) написать X ср.
Применяем практически те же шаги:
1. Найти среднее арифметическое выборки:
Xср = (9 + 2 + 5 + 4 + 12 + 7) / 6 = 39 / 6 = 6,5
2. От каждого значения выборки отнять среднее арифметическое:
X1 – Xср = 9 – 6,5 = 2,5
X2 – Xср = 2 – 6,5 = –4,5
X3 – Xср = 5 – 6,5 = –1,5
X4 – Xср = 4 – 6,5 = –2,5
X5 – Xср = 12 – 6,5 = 5,5
X6 – Xср = 7 – 6,5 = 0,5
3. Каждую полученную разницу возвести в квадрат:
(X1 – Xср)² = (2,5)² = 6,25
(X2 – Xср)² = (–4,5)² = 20,25
(X3 – Xср)² = (–1,5)² = 2,25
(X4 – Xср)² = (–2,5)² = 6,25
(X5 – Xср)² = 5,5² = 30,25
(X6 – Xср)² = 0,5² = 0,25
4. Сделать сумму полученных значений:
Σ (Xi – Xср)² = 6,25 + 20,25+ 2,25+ 6,25 + 30,25 + 0,25 = 65,5
5. Поделить на размер выборки, вычитав перед этим 1 (т.е. на n–1):
(Σ (Xi – Xср)²)/(n-1) = 65,5 / (6 – 1) = 13,1
6. Найти квадратный корень:
S = √((Σ (Xi – Xср)²)/(n–1)) = √ 13,1 ≈ 3,6193
Дисперсия и стандартное отклонение
Стандартное отклонение равно квадратному корню из дисперсии (S = √D). То есть, если у вас уже есть стандартное отклонение и нужно рассчитать дисперсию, нужно лишь возвести стандартное отклонение в квадрат (S² = D).
Дисперсия — в статистике это «среднее квадратов отклонений от среднего». Чтобы её вычислить нужно:
- Вычесть среднее значение из каждого числа
- Возвести каждый результат в квадрат (так получатся квадраты разностей)
- Найти среднее значение квадратов разностей.
Ещё расчёт дисперсии можно сделать по этой формуле:

S² — выборочная дисперсия,
Xi — величина отдельного значения выборки,
Xср (может появляться как X̅) — среднее арифметическое выборки,
n — размер выборки.
Правило трёх сигм
Это правило гласит: вероятность того, что случайная величина отклонится от своего математического ожидания более чем на три стандартных отклонения (на три сигмы), почти равна нулю.
Глядя на рисунок нормального распределения случайной величины, можно понять, что в пределах:
- одного среднеквадратического отклонения заключаются 68,26% значений (Xср ± 1σ или μ ± 1σ),
- двух стандартных отклонений — 95,44% (Xср ± 2σ или μ ± 2σ),
- трёх стандартных отклонений — 99,72% (Xср ± 3σ или μ ± 3σ).
Это означает, что за пределами остаются лишь 0,28% — это вероятность того, что случайная величина примет значение, которое отклоняется от среднего более чем на 3 сигмы.
Стандартное отклонение в excel
Вычисление стандартного отклонения с «n – 1» в знаменателе (случай выборки из генеральной совокупности):
1. Занесите все данные в документ Excel.
2. Выберите поле, в котором вы хотите отобразить результат.
3. Введите в этом поле «=СТАНДОТКЛОНА(«
4. Выделите поля, где находятся данные, потом закройте скобки.
5. Нажмите Ввод (Enter).
В случае если данные представляют всю генеральную совокупность (n в знаменателе), то нужно использовать функцию СТАНДОТКЛОНПА.
Коэффициент вариации
Коэффициент вариации — отношение стандартного отклонения к среднему значению, т.е. Cv = (S/μ) × 100% или V = (σ/X̅) × 100%.
Стандартное отклонение делится на среднее и умножается на 100%.
Можно классифицировать вариабельность выборки по коэффициенту вариации:
- при <10% выборка слабо вариабельна,
- при 10% – 20 % — средне вариабельна,
- при >20 % — выборка сильно вариабельна.
Узнайте также про:
- Корреляции,
- Метод Крамера,
- Метод наименьших квадратов,
- Теорию вероятностей
- Интегралы.
Загрузить PDF
Загрузить PDF
Вычислив среднеквадратическое отклонение, вы найдете разброс значений в выборке данных.[1]
Но сначала вам придется вычислить некоторые величины: среднее значение и дисперсию выборки. Дисперсия – мера разброса данных вокруг среднего значения.[2]
Среднеквадратическое отклонение равно квадратному корню из дисперсии выборки. Эта статья расскажет вам, как найти среднее значение, дисперсию и среднеквадратическое отклонение.
-
1
Возьмите наборе данных. Среднее значение – это важная величина в статистических расчетах.[3]
- Определите количество чисел в наборе данных.
- Числа в наборе сильно отличаются друг от друга или они очень близки (отличаются на дробные доли)?
- Что представляют числа в наборе данных? Тестовые оценки, показания пульса, роста, веса и так далее.
- Например, набор тестовых оценок: 10, 8, 10, 8, 8, 4.
-
2
Для вычисления среднего значения понадобятся все числа данного набора данных.[4]
- Среднее значение – это усредненное значение всех чисел в наборе данных.
- Для вычисления среднего значения сложите все числа вашего набора данных и разделите полученное значение на общее количество чисел в наборе (n).
- В нашем примере (10, 8, 10, 8, 8, 4) n = 6.
-
3
Сложите все числа вашего набора данных.[5]
- В нашем примере даны числа: 10, 8, 10, 8, 8 и 4.
- 10 + 8 + 10 + 8 + 8 + 4 = 48. Это сумма всех чисел в наборе данных.
- Сложите числа еще раз, чтобы проверить ответ.
-
4
Разделите сумму чисел на количество чисел (n) в выборке. Вы найдете среднее значение.[6]
- В нашем примере (10, 8, 10, 8, 8 и 4) n = 6.
- В нашем примере сумма чисел равна 48. Таким образом, разделите 48 на n.
- 48/6 = 8
- Среднее значение данной выборки равно 8.
Реклама
-
1
Вычислите дисперсию. Это мера разброса данных вокруг среднего значения.[7]
- Эта величина даст вам представление о том, как разбросаны данные выборки.
- Выборка с малой дисперсией включает данные, которые ненамного отличаются от среднего значения.
- Выборка с высокой дисперсией включает данные, которые сильно отличаются от среднего значения.
- Дисперсию часто используют для того, чтобы сравнить распределение двух наборов данных.
-
2
Вычтите среднее значение из каждого числа в наборе данных. Вы узнаете, насколько каждая величина в наборе данных отличается от среднего значения.[8]
- В нашем примере (10, 8, 10, 8, 8, 4) среднее значение равно 8.
- 10 — 8 = 2; 8 — 8 = 0, 10 — 2 = 8, 8 — 8 = 0, 8 — 8 = 0, и 4 — 8 = -4.
- Проделайте вычитания еще раз, чтобы проверить каждый ответ. Это очень важно, так как полученные значения понадобятся при вычислениях других величин.
-
3
Возведите в квадрат каждое значение, полученное вами в предыдущем шаге.[9]
- При вычитании среднего значения (8) из каждого числа данной выборки (10, 8, 10, 8, 8 и 4) вы получили следующие значения: 2, 0, 2, 0, 0 и -4.
- Возведите эти значения в квадрат: 22, 02, 22, 02, 02, и (-4)2 = 4, 0, 4, 0, 0, и 16.
- Проверьте ответы, прежде чем приступить к следующему шагу.
-
4
Сложите квадраты значений, то есть найдите сумму квадратов.[10]
- В нашем примере квадраты значений: 4, 0, 4, 0, 0 и 16.
- Напомним, что значения получены путем вычитания среднего значения из каждого числа выборки: (10-8)^2 + (8-8)^2 + (10-2)^2 + (8-8)^2 + (8-8)^2 + (4-8)^2
- 4 + 0 + 4 + 0 + 0 + 16 = 24.
- Сумма квадратов равна 24.
-
5
Разделите сумму квадратов на (n-1). Помните, что n – это количество данных (чисел) в вашей выборке. Таким образом, вы получите дисперсию.[11]
- В нашем примере (10, 8, 10, 8, 8, 4) n = 6.
- n-1 = 5.
- В нашем примере сумма квадратов равна 24.
- 24/5 = 4,8
- Дисперсия данной выборки равна 4,8.
Реклама
-
1
Найдите дисперсию, чтобы вычислить среднеквадратическое отклонение.[12]
- Помните, что дисперсия – это мера разброса данных вокруг среднего значения.
- Среднеквадратическое отклонение – это аналогичная величина, описывающая характер распределения данных в выборке.
- В нашем примере дисперсия равна 4,8.
-
2
Извлеките квадратный корень из дисперсии, чтобы найти среднеквадратическое отклонение.[13]
- Как правило, 68% всех данных расположены в пределах одного среднеквадратического отклонения от среднего значения.
- В нашем примере дисперсия равна 4,8.
- √4,8 = 2,19. Среднеквадратическое отклонение данной выборки равно 2,19.
- 5 из 6 чисел (83%) данной выборки (10, 8, 10, 8, 8, 4) находится в пределах одного среднеквадратического отклонения (2,19) от среднего значения (8).
-
3
Проверьте правильность вычисления среднего значения, дисперсии и среднеквадратического отклонения. Это позволит вам проверить ваш ответ.[14]
- Обязательно записывайте вычисления.
- Если в процессе проверки вычислений вы получили другое значение, проверьте все вычисления с самого начала.
- Если вы не можете найти, где сделали ошибку, проделайте вычисления с самого начала.
Реклама
Об этой статье
Эту страницу просматривали 64 925 раз.
Была ли эта статья полезной?
Разброс (иногда
эту величину называют размахом)
выборки
обозначается буквой R.
Это самый
простой показатель, который можно
получить для выборки — разность между
максимальной и минимальной величинами
данного конкретного вариационного
ряда, т.е.
R
= X
— X
тaх
тiт
Понятно, что чем
сильнее варьирует измеряемый признак,
тем больше величина R,
и наоборот.
Однако может
случиться так, что у двух выборочных
рядов и средние, и размах совпадают,
однако характер варьирования этих рядов
будет различный. Например, даны две
выборки:
X
= 10 15 20 25
30 35 40 45 50
= 30 R
= 40
Y
= 10 28 28 30
30 30 32 32 50
= 30 R
= 40
При равенстве
средних и разбросов для этих двух
выборочных рядов характер их варьирования
различен. Для того чтобы более четко
представлять характер варьирования
выборок, следует обратиться к их
распределениям.
4.5. Дисперсия
Рассмотрим еще
одну очень важную числовую характеристику
выборки, называемую дисперсией.
Дисперсия
представляет собой наиболее часто
использующуюся меру рассеяния случайной
величины (переменной). Дисперсия
это среднее
арифметическое квадратов отклонений
значений переменной от её среднего
значения.
49
(4.4)
где
п — объем
выборки
i—
индекс суммирования
— среднее,
вычисляемое по формуле (4.1).
Вычислим дисперсию
следующего ряда
2 4 6 8 10
(4.5)
Прежде всего найдем
среднее ряда (4.5). Оно равно X
= 6.
Рассмотрим величины:
(Xj
— X)
для каждого
элемента ряда. Иными словами, из каждого
элемента ряда 4.5 вычтем величину среднего
этого ряда. Полученные величины
характеризуют то, насколько каждый
элемент отклоняется от средней величины
в данном ряду. Обозначим полученную
совокупность разностей как множество
Т. Тогда
Г есть:
T
= (2 — 6 = -4; 4 — 6 = -2; 6 — 6 = 0; 8 — 6 = 2; 10 — 6 = 4).
Так образуется
новый ряд чисел. Его особенность в том,
что при сложении этих чисел обязательно
получится ноль. Проверим: (-4) + (-2) + 0 +
2 + 4 = 0.
Отметим, что сумма
такого ряда ∑(Xi
—
)
всегда будет
равна нулю.
Для того чтобы
избавиться от нуля, каждое значение
разности (Xi
—
)
возводят в
квадрат, все их суммируют и затем делят
на число элементов, т.е. применяют формулу
4.4. В нашем примере получится следующее:
=
(-4)
(-4)+(-2)-(-2)+ = 16 + 4 + 0 + 4 + 16 = 40
Это и есть искомая
дисперсия.
Общий алгоритм
вычисления дисперсии для одной выборки
следующий:
50
1. Вычисляется
среднее по выборке.
2. Для каждого
элемента выборки вычисляется его
отклонение от
средней, т.е.
получается множество Т.
3. Каждый элемент
множества T
возводят в квадрат.
4. Находится сумма
этих квадратов.
5. Эта сумма, как
и в случае вычисления среднего, делится
на общее количество членов ряда — я. В
ряде случаев, особенно когда величина
выбоки мала, деление осуществляется не
на величину п,
а на величину
п — 1.
Величина, получающаяся
после пятого шага, и есть искомая
дисперсия.
Расчет дисперсии
для таблицы чисел осуществляется по
формуле 4.6:
(4.6)
где ху
— значения
всех переменых, полученных в эксперименте,
или все элементы таблицы;
индексу меняется
от 1 до p,
где р число
столбцов в таблице, а индекс i
меняется
от 1 до п, где
п — число
испытуемых или число строк в таблице.
—общая средняя
всех элементов таблицы, вычисленная по
формуле 4.3;
N — общее
число всех элементов в таблице
(анализируемой совокупности
экспериментальных данных) и в общем
случае N = р
-п.
Дисперсию для
генеральной совокупности принято
обозначать как σ2,
а дисперсию выборки как
,
причем индекс
х обозначает,
что дисперсия характеризует варьирование
числовых значений признака вокруг их
средней арифметической.
Преимущество
дисперсии перед размахом в том, что
дисперсию можно представить как
сумму ряда чисел (согласно ее оп-
51
ределению), т.е.
разложить на составные компоненты,
позволяя тем самым более подробно
охарактеризовать исходную выборку.
Важная характеристика дисперсии
заключается также и в том, что с её
помощью можно сравнивать выборки,
различные по объему.
Однако сама
дисперсия, как характеристика отклонения
от среднего, часто неудобна для
интерпретации. Так, например, предположим,
что в эксперименте измерялся рост в
сантиметрах, тогда размерность
дисперсии будет являться характеристикой
площади, а не линейного размера (поскольку
при подсчете дисперсии сантиметр
возводится в квадрат).
Для того чтобы
приблизить размерность дисперсии к
размерности измеряемого признака
применяют операцию извлечения квадратного
корня из дисперсии. Полученную величину
называют стандартным
отклонением.
Из суммы квадратов,
деленных на число членов ряда извлекается
квадратный корень.
(4.7)
Другими словами,
стандартное отклонение выборки Sx
представляет
собой корень квадратный, извлеченный
из дисперсии
выборки
. Стандартное отклонение для генеральной
совокупности обозначают также
символом а. Подчеркнем еще раз, что
размерность стандартного отклонения
и размерность исходного ряда совпадают.
В нашем примере
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Дисперсия Значение
В статистике дисперсия (или разброс) — это средство описания степени распределения данных вокруг центрального значения или точки. Это помогает понять распределение данных. Более низкая дисперсия указывает на более высокую точность производственного процесса или измерения данных, тогда как более высокая дисперсия означает более низкую точность.
Можно использовать дисперсию, чтобы понять изменение значений набора данных. Это помогает количественно оценить качество данных. В финансах он позволяет инвесторам определять статистическое распределение вероятной отдачи от своих инвестиций. Диапазон, дисперсия, среднее отклонение и стандартное отклонение являются одними из распространенных показателей дисперсии.
Оглавление
- Дисперсия Значение
- Объяснение дисперсии в статистике
- Меры дисперсии в статистике
- #1 – Абсолютная мера
- #2 – Относительная мера
- Примеры
- Пример №1
- Пример #2
- Часто задаваемые вопросы
- Рекомендуемые статьи
- Дисперсия означает расстояние разбросанных данных от центрального значения данных.
- Он дает информацию о волатильности или энергонезависимости набора данных. Большее расстояние от центральной точки означает более изменчивый характер, и наоборот.
- В финансах дисперсия обратно пропорциональна эффективности, доходности или производительности ценных бумаг.
- Мера дисперсии может быть абсолютной или относительной. Абсолютные показатели имеют ту же единицу измерения, что и данный набор данных, а относительные показатели выражаются в виде отношений и процентов.
Объяснение дисперсии в статистике
Дисперсия (разброс или вариация) может иметь несколько значений в зависимости от контекста, в котором она используется. Например, в статистике это фактор, который помогает определить степень вариации значений в конкретном наборе данных.
В то же время он позволяет инвесторам оценить статистическое распределение потенциальной доходности портфеля. Доходность портфеля. Формула доходности портфеля рассчитывает доходность всего портфеля, состоящего из различных отдельных активов. Формула рассчитывается путем вычисления рентабельности инвестиций в отдельный актив, умноженной на соответствующую весовую категорию в общем портфеле, и сложения всех результатов вместе. Rp = ∑ni=1 Читать далее в финансах. Таким образом, разброс — это измерение изменчивости элемента по сравнению с другими элементами в наборе данных и его центрального значения.
Обычно с помощью меры центральной тенденцииcCentral TendencCentral Tendency — это статистическая мера, которая отображает центральную точку всего распределения данных, и вы можете найти ее, используя 3 различных меры, т. е. среднее значение, медиану и моду. подробнее, чтобы описать определенный набор данных недостаточно. Мера центральной тенденции может помочь узнать среднее значение, медиану или моду наборов данных, но меру вариации можно узнать только через дисперсию. Следовательно, анализ данных с использованием статистики осуществляется:
- Мера центральной тенденции
- Мера рассеивания (MOD)
Измерение спреда дает нам точную информацию о статистике вертикального распределения данных в соответствии с гистограммой. Однако информация, полученная из него, больше связана с разделением точек данных, разницей в значениях набора данных и расстоянием каждой отдельной точки данных от среднего значения всего набора данных.
Другими словами, он показывает, как данные распределены и насколько они отличаются друг от друга, т. е. однородность или неоднородность данных в распределении. Если расстояние между точкой данных и ее средним значением равно:
- Более того, говорят, что набор данных изменчив.
- Меньше, то данные считаются менее изменчивыми, более безопасными или высокодоходными.
Меры дисперсии в статистике
Существует два метода измерения степени изменчивости набора данных:
- Абсолютная мера
- Относительная мера
#1 – Абсолютная мера
Это относится к среднему значению отклонений данных, таких как стандартное отклонение или среднее отклонение. Он имеет ту же единицу измерения, что и исходный набор данных, например, сантиметры, метры, килограммы и т. д. Вот некоторые абсолютные меры разброса.
- Диапазон (клавиша R)
Диапазон относится к разнице между наибольшим и наименьшим значениями в заданном наборе данных. Чем выше значение диапазона, тем выше разброс данных.
Р = Л — Д
где,
L = наибольшее значение
S = наименьшее значение
- Квартильное отклонение (QD)
Квартиль распределяет набор данных по четырем наборам с одинаковыми значениями. Каждый набор данных имеет наименьшее число, наибольшее число и медиану. Q2 или второй квартиль — это медиана данных. Первый квартиль (Q1) соединяет наименьшее число с Q2, а третий квартиль (Q3) соединяет наибольшее число с Q2.
Межквартильный размах – это разница между третьим квартилем и первым квартилем. Половина межквартильного диапазона представляет собой квартильное отклонение.
Следовательно, межквартильный размах (IR) = Q3 – Q1.
- Коэффициент диапазона (COR)
Это отношение разницы между наибольшим и наименьшим значениями в распределении к сумме наибольшего и наименьшего значений в распределении.
КОР = LS/L+S
где,
L= наибольшее значение
S = наименьшее значение
- Коэффициент вариации (COV)
Он используется для сопоставления двух наборов данных на основе их согласованности.
где,
Х = среднее
σ = стандартное отклонение
- Коэффициент стандартного отклонения (COS)
Это стандартное отклонение, деленное на среднее значение набора данных.
COS = SD/среднее
где,
SD — стандартное отклонение
- Коэффициент квартильного отклонения (COQ)
Это отношение разницы между третьим и первым квартилем к сумме третьего и первого квартиля набора данных.
COQ = Q3 – Q1/ Q3 + Q1
- Коэффициент среднего отклонения (COM):
Он рассчитывается с использованием среднего значения, медианы или режима данных.
COM = MD/среднее
Или
COM = MD/медиана
Или
COM = MD/режим
где,
MD = среднее отклонение
Примеры
Давайте рассмотрим следующие примеры дисперсии для лучшего понимания концепции.
Пример №1
Возьмем пример с фондового рынка. Рынок акций. Рынок акций работает по основному принципу согласования спроса и предложения посредством аукционного процесса, когда инвесторы готовы заплатить определенную сумму за актив и готовы продать то, что у них есть, по более низкой цене. конкретная цена.читать дальше домен. На бирже торгуется некая ценная бумага А. Трейдеры, которые хотят инвестировать в ценную бумагу А, будут смотреть на ее исторические данные о доходности за последний год. Они оценят степень рассеяния прибыли безопасности за последний год.
Чем меньше степень рассеяния доходностей, тем меньше колебания цен. Таким образом, ценная бумага будет считаться более безопасной инвестицией с низким уровнем риска. Инвестиции с низким уровнем риска. Инвестиции с низким уровнем риска — это финансовые инструменты с минимальной неопределенностью или вероятностью потерь для инвесторов. Хотя такие инвестиции безопасны, они не могут предложить инвесторам высокую прибыль. читать далее. Более того, если степень распространения ценной бумаги А выше, это означает, что цена сильно волатильна. Поэтому ценная бумага будет восприниматься как ненадежная инвестиция в таком случае.
Другими словами, более высокая дисперсия означает более рискованные инвестиции и наоборот.
Пример #2
Рассмотрим два сорта кофе — X и Y с разным выходом.
Кофе X и Y имеют следующие урожаи за шесть месяцев:
Сорт кофеЯнварьФевральМартАпрельМайИюньX363132343033Y584233295020
Чтобы узнать распространение каждого сорта кофе, рассчитаем его ассортимент.
Диапазон (R) = наибольшее значение (L) – наименьшее значение (S)
Сорт кофеНаибольшее значение (L) Наименьшее значение (S) Диапазон (R = L – S)X36306Y582038
Как упоминалось ранее, чем выше диапазон, тем больше разброс данных. Таким образом,
- X имеет более низкий диапазон. Это означает, что у него меньше разбросанных данных или более однородный набор данных.
- Y имеет более высокий диапазон. Он представляет собой сильно разбросанный набор данных или более разнородный набор данных.
Следовательно, X имеет более низкий спред, чем Y. Более низкий спред означает более высокую доходность, а более высокий спред означает более низкую доходность. Следовательно, более высокая дисперсия в данных означает меньшую отдачу, а более низкая дисперсия в наборе данных означает более высокую отдачу.
Часто задаваемые вопросы
Что означает дисперсия в статистике?
Дисперсия означает масштаб распределения данных вокруг центральной точки или значения. Он показывает расстояние значений в распределении от центрального значения. Он играет важную роль в оценке изменчивости, качества и выхода наборов данных при статистическом наблюдении.
Что вызывает дисперсию?
Разброс данных происходит в статистике из-за природных явлений, неравномерного поведения данных наблюдений, а также из-за технических погрешностей приборов измерения данных. Все эти факторы способствуют разбросу данных в статистике.
Каковы три меры дисперсии?
Дисперсия измеряется в абсолютном или относительном выражении. Наиболее часто используемыми показателями разброса являются диапазон, дисперсия и стандартное отклонение. Диапазон — это разница между самым высоким и самым низким значением в распределении. Дисперсия получается путем сложения квадрата разницы между каждым значением в распределении и средним значением, а затем делением его на количество значений в наборе данных. Стандартное отклонение — это квадратный корень из дисперсии.
Рекомендуемые статьи
Это было руководство по дисперсии в статистике и ее значению. Здесь мы обсуждаем меры дисперсии данных в распределении вместе с примерами. Вы можете узнать больше о бухгалтерском учете из следующих статей –
- Нормальное распределение
- Центральная предельная теорема
- Усеченное среднее