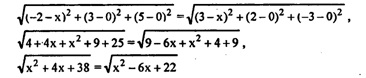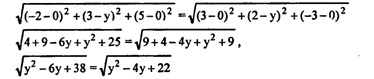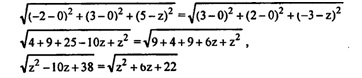Как найти равноудаленную точку от четырех точек - AvtoShod.ru

Точка, равноудалённая от четырёх точек, — это точка, образованная пересечением трёх равноудалённых плоскостей, для пар одной точки с другими точками (при однозначном определении равноудалённой плоскости для двух точек).

Обозначения

Введём обозначения:

— радиус-вектор равноудалённой точки;

— радиус-вектор первой точки;

— радиус-вектор второй точки;

— радиус-вектор третьей точки;

— радиус-вектор четвёртой точки;

— нормаль к первой плоскости;

— нормаль ко второй плоскости;

— нормаль к третьей плоскости;

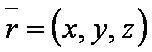
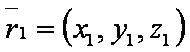
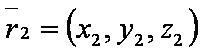
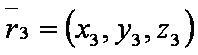
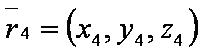
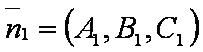
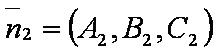
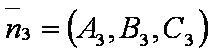
— уравнение первой плоскости;

— уравнение второй плоскости;

— уравнение третьей плоскости.

Формулы:

Векторная форма:

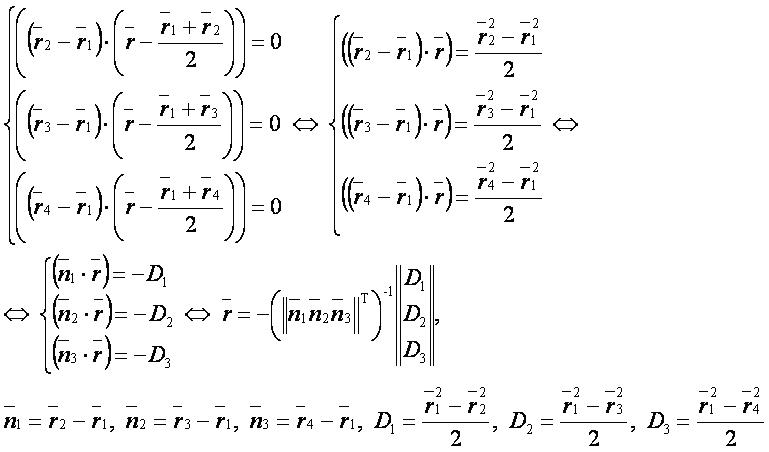
Координатная форма:

Заметим, что равноудалённая точка является центром сферы, проходящей через заданные четыре точки.

Другие формулы:

Основание перпендикуляра из точки к прямой;
Основание перпендикуляра из точки к плоскости;
Точка пересечения перпендикуляра к двум прямым с первой прямой;
Точка пересечения перпендикуляра к двум прямым со второй прямой;
Точка пересечения прямой и плоскости;
Точка пересечения трёх плоскостей;
Точка, равноудалённая от двух прямых;
Точка, равноудалённая от четырёх точек;
Точка деления отрезка в данном отношении;
Точка прямой, находящаяся от первой точки прямой до второй в данном отношении;
Точка прямой, находящаяся перед первой точкой прямой до второй в данном отношении;
Точка прямой, находящаяся от первой точки прямой за второй в данном отношении.

Ссылки

Участник:Logic-samara

Источник

Точка, равноудалённая от четырёх точек — точка, образованная пересечением трёх равноудалённых плоскостей, для пар одной точки с другими точками (при однозначном определении равноудалённой плоскости для двух точек).

Обозначения[править]

Введём обозначения:

— радиус-вектор равноудалённой точки;

${displaystyle {bar {r}}_{1}=(x_{1},y_{1},z_{1})}$ — радиус-вектор первой точки;

${displaystyle {bar {r}}_{2}=(x_{2},y_{2},z_{2})}$ — радиус-вектор второй точки;

${displaystyle {bar {r}}_{3}=(x_{3},y_{3},z_{3})}$ — радиус-вектор третьей точки;

${displaystyle {bar {r}}_{4}=(x_{4},y_{4},z_{4})}$ — радиус-вектор четвёртой точки;

${displaystyle {bar {n}}_{1}=(A_{1},B_{1},C_{1})}$ — нормаль к первой плоскости;

${displaystyle {bar {n}}_{2}=(A_{2},B_{2},C_{2})}$ — нормаль ко второй плоскости;

${displaystyle {bar {n}}_{3}=(A_{3},B_{3},C_{3})}$ — нормаль к третьей плоскости;

${displaystyle A_{1}x+B_{1}y+C_{1}z+D_{1}=0}$ — уравнение первой плоскости;

${displaystyle A_{2}x+B_{2}y+C_{2}z+D_{2}=0}$ — уравнение второй плоскости;

${displaystyle A_{3}x+B_{3}y+C_{3}z+D_{3}=0}$ — уравнение третьей плоскости.

Формулы[править]

Векторная форма:

Координатная форма:

Заметим, что равноудалённая точка является центром сферы, проходящей через заданные четыре точки.

Другие формулы[править]

Основание перпендикуляра из точки к прямой;
Основание перпендикуляра из точки к плоскости;
Точка пересечения перпендикуляра к двум прямым с первой прямой;
Точка пересечения перпендикуляра к двум прямым со второй прямой;
Точка пересечения прямой и плоскости;
Точка пересечения трёх плоскостей;
Точка, равноудалённая от четырёх точек;
Точка деления отрезка в данном отношении;
Точка прямой, находящаяся от первой точки прямой до второй в данном отношении;
Точка прямой, находящаяся перед первой точкой прямой до второй в данном отношении;
Точка прямой, находящаяся от первой точки прямой за второй в данном отношении.
уравнения.

Источник

Tutorials
Alpha	Angle of 60° • Perpendicular Bisector • Midpoint • Circle in Square • Rhombus in Rectangle • Circle Center • Inscribed Square
Beta	Angle Bisector • Intersection of Angle Bisectors • Angle of 30° • Double Angle • Cut Rectangle • Drop a Perpendicular • Erect a Perpendicular • Tangent to Circle at Point • Circle Tangent to Line • Circle in Rhombus
Gamma	Chord Midpoint • Triangle by Angle and Orthocenter • Intersection of Perpendicular Bisectors • Three equal segments — 1 • Circle through Point Tangent to Line • Midpoints of Trapezoid Bases • Angle of 45° • Lozenge • Center of Quadrilateral
Delta	Double Segment • Angle of 60° — 2 • Circumscribed Equilateral Triangle • Equilateral Triangle in Circle • Cut Two Rectangles • Square Root of 2 • Square Root of 3 • Angle of 15° • Square by Opposite Midpoints • Square by Adjacent Midpoints • Square by Two Vertices
Epsilon	Parallel Line • Parallelogram by Three Vertices • Line Equidistant from Two Points — 1 • Line Equidistant from Two Points — 2 • Hash • Shift Angle • Line Equidistant from Two Lines • Circumscribed Square • Square in Square • Circle Tangent to Square Side • Regular Hexagon
Zeta	Point Reflection • Reflection • Copy Segment • Given Angle Bisector • Non-collapsing Compass • Translate Segment • Triangle by Three Sides • Parallelogram • Nine Point Circle • Symmetry of Four Lines • Parallelogram by Three Midpoints
Eta	Sum of Areas of Squares • Annulus • Angle of 75° • Line Equidistant from Three Points • Heron’s Problem • Circumscribed Circle • Inscribed Circle • Circle Tangent to Three Lines • Segment by Midpoint • Angle Isosceles • Excircle
Theta	Perimeter Bisector • Angle 54° Trisection • Interior Angles • Regular Octagon • Triangle Cleaver • Torricelli Point • Circle Equidistant from Four Points • Octagon from Square • Egyptian Triangle by Side of Length 4 • Chord Parallel to Segment
Iota	Minimum Perimeter — 1 • Third Proportional • Harmonic Mean of Trapezoid Bases • Drop a Perpendicular* • Midpoint* • Trisection by Trapezoid Diagonals • Minimum Perimeter — 2 • Harmonic Mean of Segments • Triangle by Angle and Centroid • Triangle Mid-Segment
Kappa	Tangent of Circle • Outer Tangent • Inner Tangent • Rotation 90° • Rotation 60° • Segment Trisection • Segment Trisection* • Chord Trisection • Three Circles — 1 • Secant Bisection • Three Circles — 2 • Center of Rotation
Lambda	Fourth Proportional • Geometric Mean of Segments • Golden Section • Angle of 54° • Third Parallel Line • Circle in Angle • Geometric Mean of Trapezoid Bases • Regular Pentagon • Point Farthest from Angle Sides • Ratio 1 to 5
Mu	Triangle by Midpoints • Triangle by Side and Centroid • Triangle by Altitude Base Points • Triangle by Tangent Points • Triangle by Excenters • Equilateral Triangle by Centroid and Two Points • Right Triangle by Two Points on Legs • Hypotenuse and Altitude • Hypotenuse and Leg • Isosceles Triangle by Tangent Points
Nu	Circle Tangent to Line and Circle • Equilateral Triangle — 2 • Equilateral Triangle on Concentric Circles • Square in Triangle • Point Equidistant from Side of Angle and Point • Circle Through Two Points and Tangent to Line • Inscribed Square — 2 • Line Reflection • Square by Four Points
Xi	Rhombus in Triangle • Circle Tangent to Two Circles • Triangle by Tangent Point on Hypotenuse • Parallelogram on Four Lines • Arbelos
Omicron	Midpoint* • Copy Circle • Line-Circle Intersection • Three Equal Segments • Tangent to Circle* • Napoleon’s Problem • Drop a Perpendicular** • Line-Circle Intersection* • Circle with Center on Line • Angle of 3° • Mickey Mouse
Equilateral Triangle • Intersect Tool • Perpendicular Bisector • Move Tool • Angle Bisector • Perpendicular • Parallel Line • Compass

Источник

��

�� , ��̣�� ң� �� . ��
�� ?

��

��: 7 �� (� �� ).

�� A, B, C, D — �� , S — �� . ��
�� S �� k �� , �� 4 — k ��
��. �� , ��
(�� S �� ; ��
�� ). �� ,
1k3. ��
�� S: 2 + 2 � 1 + 3.

�� A � B �� S, �
�� C � D — �� . �� S �� O
�� AB � CD. ��
�� S �� OA � OC.
�� , �� 3
��.

�� A, B � C �� S,
� �� D — �� . ��ģ� �� A, B � C ��.
�� O � R — ţ �� . �� O ��
��, � �� R �
OD. �� ң� �� , ��
�� 4 ��.

��

Источник

Расстояние между двумя точками
а) Пусть С (х; 0; 0) — точка на оси Ох, равноудаленная от точек А и В. Следовательно, СА=СВ, или в координатах:

х²+4х+3 8=х² — 6х+22, 10х= -16, х= — 1,6; С (- 1,6; 0; 0).
Равноудаленной от точек А и В будет точка С (-1,6; 0; 0).
б) Пусть D (0; у, 0) — точка на оси Оу, равноудаленная от А и В. AD=DB.

у² -бу+38=y² -4у+22 2у=16, у=8; D (0; 8; 0).
в) Пусть Е (0; 0; z) —точка на оси Oz, равноудаленная от А и В.

z²-10z+3 8=z²+6z+22, 16z = 16, z= 1 ; E (0; 0; 1 ).