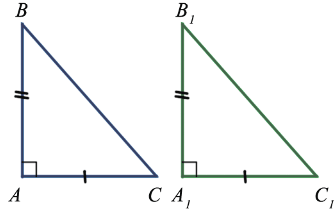
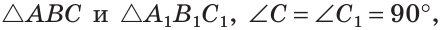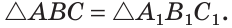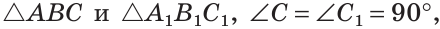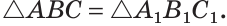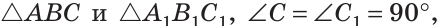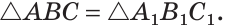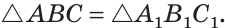Теорема 1
(Признак равенства прямоугольных треугольников по катету и прилежащему острому углу)
Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого прямоугольного треугольника, то такие треугольники равны.
Дано:
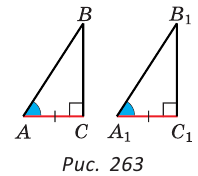
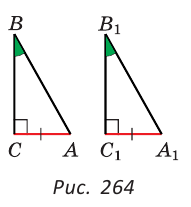
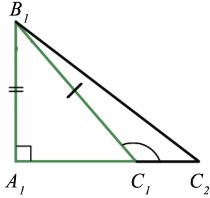
ΔABC, ΔA1B1C1,
∠C=90°, ∠C1=90°,
BC=B1C1, ∠B=∠B1
Доказать: ΔABC= ΔA1B1C1
Доказательство:
По условию, в треугольниках ABC и ΔA1B1C1:
1) BC=B1C1;
2)∠C=∠C1;
3) ∠B=∠B1.
Следовательно, ΔABC= ΔA1B1C1(по стороне и двум прилежащим к ней углам).
Что и требовалось доказать.
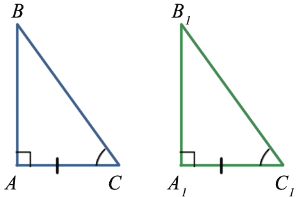
Теорема 2
(Признак равенства прямоугольных треугольников по катету и противолежащему углу)
Если катет и противолежащий ему угол одного прямоугольного треугольника соответственно равны катету и противолежащему ему углу другого прямоугольного треугольника, то такие треугольники равны.
Дано:
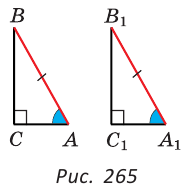
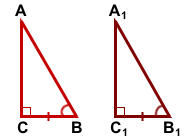
ΔABC, ΔA1B1C1,
∠C=90°, ∠C1=90°, BC=B1C1,
∠A=∠A1
Доказать: ΔABC= ΔA1B1C1
Доказательство:
По условию, в треугольниках ABC и ΔA1B1C1:
1) BC=B1C1;
2)∠C=∠C1;
3)Так как сумма острых углов прямоугольного треугольника равна 90°,
то есть ∠ B=∠ B1.
Следовательно, ΔABC= ΔA1B1C1(по стороне и двум прилежащим к ней углам).
Что и требовалось доказать.
Преподаватель который помогает студентам и школьникам в учёбе.
Признаки равенства прямоугольных треугольников с примерами решения
Содержание:
Признаки равенства прямоугольных треугольников:
Вы уже знаете три признака равенства треугольников. Поскольку часто приходится иметь дело с прямоугольными треугольниками, то выделяют пять признаков равенства прямоугольных треугольников. Сформулируем и докажем их.
Второй признак (по катету и прилежащему острому углу)
Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого прямоугольного треугольника, то такие треугольники равны.
Дано: 
Доказать: 
Доказательство:
по стороне и двум прилежащим к ней углам.
Третий признак (по катету и противолежащему острому углу)
Если катет и противолежащий острый угол одного прямоугольного треугольника соответственно равны катету и противолежащему острому углу другого прямоугольного треугольника, то такие треугольники равны.
Дано: 
(рис. 264).
Доказать: 
Доказательство:
Сумма острых углов прямоугольного треугольника равна 90°. Из того, что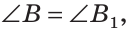 
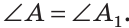
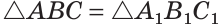
следует, что 
Тогда 
по стороне и двум прилежащим к ней углам.
Четвертый признак (по гипотенузе и острому углу)
Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны.
Дано: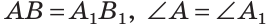 
(рис. 265).
Доказать: 
Доказательство:
Сумма острых углов прямоугольного треугольника равна 90°. Из того, что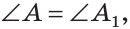 
следует, что 
Тогда 
по стороне и двум прилежащим к ней углам.
Пятый признак (по катету и гипотенузе).
Если катет и гипотенуза одного прямоугольного треугольника соответственно равны катету и гипотенузе другого прямоугольного треугольника, то такие треугольники равны.
Дано: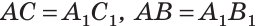 
(рис. 266).
Доказать: 
Доказательство:
Приложим треугольников А1В1С1 к треугольнику АВС так, чтобы совместились равные катеты А1С1 и АС, а вершины В1 и В лежали по разные стороны от прямой АС. Треугольник А1В1С1 займет положение треугольника АВ2С. Так как 
B2CB — развернутый и АВ2 = АВ, то треугольник В2АВ — равнобедренный, катет АС — его высота. По свойству равнобедренного треугольника высота, проведенная к основанию, будет и медианой. Тогда В2С=СВ и треугольники ABC и АВ2С равны по двум катетам.
Отсюда
Пример:
На рисунке 267 
Доказать равенство треугольников: а) 
АВС и 
ADC б) 
АОВ и 
COD.
Доказательство:
а) Рассмотрим прямоугольные треугольники ABC и ADC. У них гипотенуза АС — общая, катеты AD и ВС равны по условию. Тогда АВС =ADC по катету и гипотенузе.
б) Из равенства треугольников ABC и ADC следует равенство сторон АВ и CD (доказано в пункте а). Тогда АОВ =COD. по катету (АВ = CD) и противолежащему острому углу (
AOB =
COD как вертикальные).
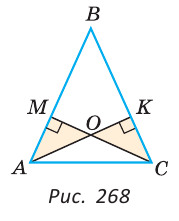
Пример:
Дан треугольник ABC, АК и СМ — его высоты, проведенные к боковым сторонам, О — точка их пересечения (рис. 268). Доказать, что если треугольники АОМ и СОК равны, то треугольник ABC — равнобедренный.
Доказательство:
Так как 
AOM =
COK как вертикальные, то 
MAO =
KCO (сумма острых углов прямоугольного треугольника 90°). Из равенства треугольников АОМ и СОК следует равенство гипотенуз АО и СО. Треугольник АОС — равнобедренный,
OAC =
OCA как углы при основании равнобедренного треугольника. Тогда 
BAC =
BCA как составленные из равных углов. Треугольник ABC равнобедренный по признаку равнобедренного треугольника. Что и требовалось доказать.
- Соотношения в прямоугольном треугольнике
- Сумма углов треугольника
- Внешний угол треугольника
- Свойство точек биссектрисы угла
- Задачи на построение по геометрии
- Угол — определение, виды, как обозначают с примерами
- Перпендикулярные прямые в геометрии
- Признаки равенства треугольников
- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Соотношения между сторонами и углами треугольника
- Признаки равенства прямоугольных треугольников
Признаки равенства прямоугольных треугольников позволяют сравнивать прямоугольные треугольники лишь по двум элементам, так как любые два прямых угла равны.
1. Признак равенства по двум катетам
Если катеты одного прямоугольного треугольника соответственно равны катетам другого, то такие треугольники равны
Данный признак следует из первого признака равенства треугольников.
Пример:
ABC = A1B1C1, т.к. AB = A1B1 и AC = A1C1.
2. Признак равенства по катету и острому углу
Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого, то такие треугольники равны
Данный признак следует из второго признака равенства треугольников.
Пример:
ABC = A1B1C1, т.к. AC = A1C1, 
C = C1
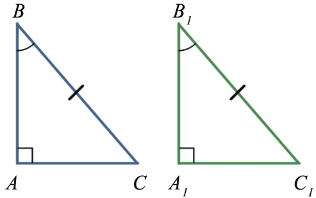
3. Признак равенства по гипотенузе и острому углу
Теорема
Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого,то такие треугольники равны
Пример:
ABC = A1B1C1, т.к. BC = B1C1, B = B1
Доказательство
Так как сумма двух острых углов прямоугольного треугольника равна 900, то в таких треугольниках два других острых угла также равны, поэтому данные треугольники равны по второму признаку треугольников, т.е. по стороне(по гипотенузе) и двум прилежащим к ней углам, что и требовалось доказать.
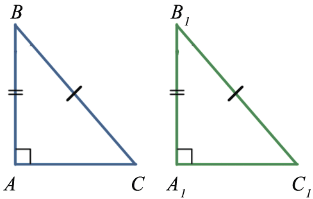
4. Признак равенства по катету и гипотенузе
Теорема
Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого, то такие треугольники равны
Пример:
ABC = A1B1C1, т.к. BC = B1C1, AB = A1B1
Доказательство
Дано: ABC, A1B1C1, BC = B1C1, AB = A1B1
Доказать: ABC = A1B1C1
Доказательство:
Рассмотрим данные треугольники:
Так как A = A1, то ABC можно наложить на A1B1C1 так, что вершина A совместится с вершиной A1, а стороны AC и AB наложатся соответственно на лучи A1C1 и A1B1. При этом вершина B совместится с вершиной B1, потому что AB = A1B1. Но тогда вершина C также совместится с вершиной C1. Действительно, если предположить, что точка C совместится с некоторой другой точкой C2 луча A1C1, то получим равнобедренный треугольник C1B1C2.
В C1B1C2 углы при основании не равны (C2 — острый, а C1 — тупой, так как он смежный с углом B1C1A1, который является острым). А это невозможно, так как у равнобедренного треугольника углы у основания равны, следовательно, вершина C совместится с вершиной C1. А это значит, что полностью совместятся треугольники ABC, A1B1C1, т.е. они равны, что и требовалось доказать.
Советуем посмотреть:
Теорема о сумме углов треугольника
Остроугольный, прямоугольный и тупоугольный треугольники
Теорема о соотношениях между сторонами и углами треугольника
Неравенство треугольника
Некоторые свойства прямоугольных треугольников
Уголковый отражатель
Расстояние от точки до прямой
Расстояние между параллельными прямыми
Построение треугольника по двум сторонам и углу между ними
Построение треугольника по стороне и двум прилежащим к ней углам
Построение треугольника по трем его сторонам
Соотношения между сторонами и углами треугольника
Правило встречается в следующих упражнениях:
7 класс
Задание 261,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 269,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 270,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 275,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 408,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 434,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 437,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 443,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 824,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 886,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
В данной публикации мы рассмотрим признаки равенства прямоугольных треугольников, изучаемые по геометрии 7 класса. Также разберем пример решения задачи для закрепления изложенного материала.
-
Равенство прямоугольных треугольников
- 1 признак
- 2 признак
-
3 признак
- 4 признак
- Пример задачи
Равенство прямоугольных треугольников
Два прямоугольных треугольника равны, если они соответствуют одному из следующих условий.
1 признак
Катет и гипотенуза первого прямоугольного треугольника равны катету и гипотенузе второго треугольника.
2 признак
Два катета первого прямоугольного треугольника равны двум катетам второго треугольника.
3 признак
Катет и острый угол первого прямоугольного треугольника равны катету и острому углу второго треугольника.
4 признак
Гипотенуза и острый угол первого прямоугольного треугольника равны гипотенузе и острому углу второго треугольника.
Пример задачи
Дана трапеция ABCD, в которой на основание AD опущены две высоты – BE и CF. При этом отрезки AE и FD равны. Докажите, что трапеция ABCD – равнобокая.
Решение
Трапеция ABCD является равнобокой, если равны AB и CD.
Опущенные на основание AD высоты образуют два прямоугольных треугольника – △ABE и △FCD.
По условиям задачи AE и FD, которые являются катетами рассматриваемых треугольников, равны.
BE и CF – это высоты трапеции, одновременно являющиеся катетами наших треугольников. Как расстояния между двумя параллельными линиями (основаниями трапеции), они также имеют одинаковую длину.
Таким образом, мы имеем два прямоугольных треугольника c равными катетами (AE=FD и BE=CF). Это является одним из признаков равенства фигур.
Это значит, что AB=CD (гипотенузы треугольников). Отсюда следует, что трапеция ABCD – равнобокая.
Признаки равенства треугольников
- Первый признак равенства треугольников
- Второй признак равенства треугольников
- Третий признак равенства треугольников
- Признаки равенства прямоугольных треугольников
Два треугольника считаются равными, если их можно совместить наложением. Но, чтобы не выполнять каждый раз наложение, для доказательства равенства треугольников, установили три признака, по которым можно определить, совместятся треугольники или нет. Эти признаки называются признаками равенства треугольников.
Первый признак равенства треугольников
Теорема:
Два треугольника равны, если у них равны две стороны и угол, лежащий между этими сторонами.
Доказательство:
Рассмотрим два треугольника 
ABC и A1B1C1, у которых:
AB = A1B1, AC = A1C1, ∠A = ∠A1.
Требуется доказать, что
ABC = A1B1C1.
Если наложить A1B1C1 на ABC так, чтобы точка A1 совместилась с точкой A и сторона A1B1 совместилась со стороной AB, то точка B совместится с точкой B1, так как A1B1 = AB. Сторона A1C1 совместится со стороной AC, так как ∠A = ∠A1. Точка C1 совпадёт с точкой C, так как A1C1 = AC. Стороны B1C1 и BC совместятся, так как совместились их концы. Таким образом, треугольники совместятся. Теорема доказана.
Второй признак равенства треугольников
Теорема:
Два треугольника равны, если у них равна одна из сторон и два прилежащих к ней угла.
Доказательство:
Рассмотрим два треугольника ABC и A1B1C1, у которых:
AC = A1C1, ∠A = ∠A1 и ∠C = ∠C1.
Требуется доказать, что
ABC = A1B1C1.
Если наложить A1B1C1 на ABC так, чтобы точка A1 совместилась с точкой A и сторона A1C1 совместилась со стороной AC, то точка C1 совпадёт с точкой C, так как A1C1 = AC. Сторона A1B1 совпадёт со стороной AB, так как ∠A = ∠A1. Сторона C1B1 совпадёт со стороной CB, так как ∠C = ∠C1. Вершина B1 совпадёт с вершиной B, так как B и B1 будут служить точками пересечения одних и тех же отрезков. Таким образом, треугольники совместятся. Теорема доказана.
Третий признак равенства треугольников
Теорема:
Два треугольника равны, если три стороны одного треугольника равны трём сторонам другого.
Доказательство:
Рассмотрим два треугольника ABC и A1B1C1, у которых:
AB = A1B1, BC = B1C1, AC = A1C1.
Требуется доказать, что
ABC = A1B1C1.
Приложим треугольники ABC и A1B1C1 один к другому так, чтобы вершина A совместилась с A1, вершина C — с C1, а вершины B и B1 оказались по разные стороны от прямой AC.
Соединив точки B и B1, получим два равнобедренных треугольника BAB1 и BСB1.
В треугольнике BAB1 ∠1 = ∠4, в BСB1 ∠2 = ∠3 (как углы при основании). Следовательно,
∠1 + ∠2 = ∠4 + ∠3, поэтому ∠ABC = ∠AB1C.
Итак, AB = A1B1, BC = B1C1, ∠ABC = ∠A1B1C1.
Из этого следует, что треугольники ABC и A1B1C1 равны по первому признаку равенства треугольников. Теорема доказана.
Признаки равенства прямоугольных треугольников
Для прямоугольных треугольников, кроме перечисленных трёх признаков равенства, имеются ещё дополнительные признаки, так как у них у всех есть прямой угол, а все прямые углы равны между собой.
Два прямоугольных треугольника будут равны в следующих четырёх случаях:
- Если катеты одного треугольника равны катетам другого.
- Если катет и прилежащий к нему острый угол одного треугольника равны катету и прилежащему к нему острому углу другого.
- Если гипотенуза и острый угол одного треугольника равны гипотенузе и острому углу другого.
- Если гипотенуза и катет одного треугольника равны гипотенузе и катету другого.
