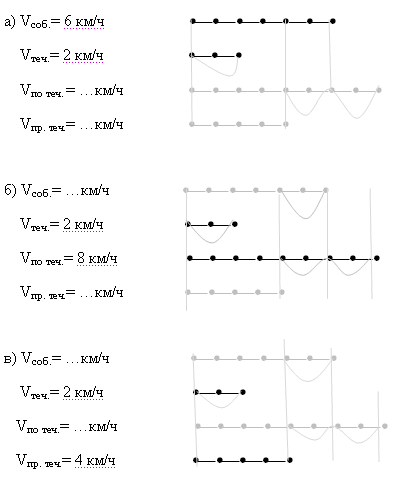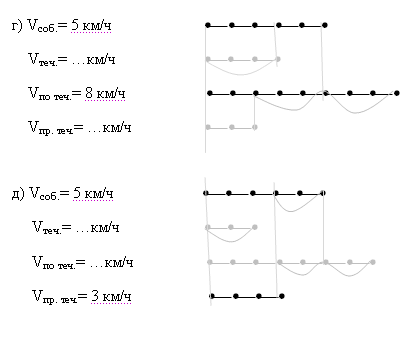В состав ЕГЭ по математике включёна целая группа задач, относящаяся к задачам на движение — это задачи на движение по воде. Задачи несложные, решаются по той же формуле. Мы уже рассматривали с вами задачи на движение «Задачи на прямолинейное движение. Часть 1» и другие. Принципы те же. Используется основная формула:
Но в задачах на движение по воде (по реке), добавляется лишь небольшое условие. Необходимо учитывать скорость течения реки. Скорость судна определяется следующим образом:
Если плыть по течению реки, то к скорости судна в неподвижной воде необходимо прибавить скорость течения.
Если плыть против течения, то из скорости судна в неподвижной воде необходимо вычесть скорость течения.
Так же необходим навык быстрого решения квадратного уравнения. На самом ЕГЭ это сэкономит ваше время. Иногда требуется извлечь корень из большого числа, по этому поводу изучите статью «Извлекаем корень из большого числа».
Рассмотрим задачи:
От пристани А к пристани В отправился с постоянной скоростью первый теплоход, а через 2 часа после этого следом за ним со скоростью, на 2 км/ч большей, отправился второй. Расстояние между пристанями равно 168 км. Найдите скорость первого теплохода, если в пункт В оба теплохода прибыли одновременно. Ответ дайте в км/ч.
Примем скорость первого теплохода за х км/ч. Тогда скорость второго теплохода равна х + 2 (км/ч).
Расстояние оба проехали одинаковое — 168 километров.
Осталось записать время.
Поскольку t = S/v, то первый затратит 168/х часов, а второй 168/(х + 2) часов.
Сказано, что через два часа после отправления первого, в путь отправился второй, то есть он затратил время на движение на два часа меньше:
Умножаем левую и правую части на х(х + 2)
Решаем квадратное уравнение:
Скорость есть величина положительная, значит, она равна 12 (км/ч).
Ответ: 12
*В этой задаче понятия «скорость течения» отсутствует и она от задач на движение по суше практически ничем не отличается.
Решите самостоятельно:
Посмотреть решение
Моторная лодка прошла против течения реки 120 км и вернулась в пункт отправления, затратив на обратный путь на 2 часа меньше. Найдите скорость лодки в неподвижной воде, если скорость течения равна 1 км/ч. Ответ дайте в км/ч.
Пусть скорость лодки в неподвижной воде равна х.
Тогда скорость движения моторки по течению равна х + 1, а скорость, с которой она движется против течения х – 1.
Расстояние и в ту, и в другую сторону одинаково и равно 120 км.
Занесем скорость и расстояние в таблицу.
Заполняем графу «время».
При движении по течению затраченное на путь время равно 120/(х + 1), при движении против течения 120/(х – 1).
Причем 120/(х + 1) на 2 часа меньше, чем 120/(х – 1).
Да это и логично, что время на движение по течению реки затрачивается меньше.
Таким образом:
Это уравнение имеет два корня: х1 = 11 х2 = –11 (оба этих числа при возведении в квадрат дают 121). Но, конечно же, отрицательный ответ не подходит — скорость лодки должна быть положительной: 11 км/ч
Ответ: 11
Решите самостоятельно:
Посмотреть решение
Теплоход проходит по течению реки до пункта назначения 560 км и после стоянки возвращается в пункт отправления. Найдите скорость теплохода в неподвижной воде, если скорость течения равна 4 км/ч, стоянка длится 8 часа, а в пункт отправления теплоход возвращается через 56 часа после отплытия из него. Ответ дайте в км/ч.
Пусть скорость теплохода в неподвижной воде равна x (км/ч). Всего теплоход затрачивает 56 часа (на весь путь: туда, два часа стоянки, обратно). То есть:
56 = (ПО ТЕЧЕНИЮ)+(СТОЯНКА)+(ПРОТИВ ТЕЧЕНИЯ)
Скорость движения теплохода по течению равна х+4 (км/ч), а скорость против течения х – 4 (км/ч).
Расстояние и в ту, и в другую сторону одинаково и равно 560 км.
Занесем скорость и расстояние в таблицу. Заполняем графу «время».
Время, затраченное на путь до пункта назначения 560/(х + 4),
Время, затраченное на путь обратно (против течения) 560/(х – 4).
Таким образом, скорость теплохода в неподвижной воде равна 24 км/ч.
Ответ: 24
Как извлекать корень из большого числа без калькулятора можно посмотреть здесь.
Решите самостоятельно:
Посмотреть решение
Теплоход проходит по течению реки до пункта назначения 459 км и после стоянки возвращается в пункт отправления. Найдите скорость течения, если скорость теплохода в неподвижной воде равна 22 км/ч, стоянка длится 10 часов, а в пункт отправления теплоход возвращается через 54 часов после отплытия из него. Ответ дайте в км/ч.
Скорость течения реки как искомую величину принимаем за x (км/ч).
Тогда скорость движения теплохода по течению равна 22 + х (км/ч), а его скорость против течения 22 – х.
Расстояние в ту, и в другую сторону одинаковое и равно 459 км.
Всего теплоход затрачивает 54 часов (на весь путь: туда, 10 часов стоянки, обратно). То есть:
54 = (ПО ТЕЧЕНИЮ)+(СТОЯНКА)+( ПРОТИВ ТЕЧЕНИЯ)
Расстояние и в ту, и в другую сторону одинаково и равно 459 км.
Занесем скорость и расстояние в таблицу. Заполняем графу «время».
Время, затраченное на путь до пункта назначения 459/(22+х),
Время, затраченное на путь обратно (против течения) 459/(22–х).
Подставляем данные и получаем уравнение:
Мы не будем подробно останавливаться на технике решения уравнения. Всё понятно — раскрываем скобки, складываем подобные члены.
Получаем квадратное уравнение: х2 = 25.
Его решением являются корни –5 и 5.
Поскольку скорость течения положительна, значит она равна 5 (км/ч).
Ответ: 5
Решить самостоятельно:
Посмотреть решение
Моторная лодка в 9:00 вышла из пункта А в пункт В, расположенный в 15 км от А. Пробыв в пункте «В» 2 часа, лодка отправилась назад и вернулась в пункт А в 19:00 того же дня. Определите (в км/ч) собственную скорость лодки, если известно, что скорость течения реки 1 км/ч.
В данной задаче несказанно, сколько лодка затратила время на путь (дан временной отрезок пути), и время стоянки.
Определим время нахождения лодки в пути 19 – 9 = 10 (часов).
Время стоянки 2 часа.
Пусть скорость лодки в неподвижной воде равна x (км/ч).
Тогда скорость движения по течению равна х+1 (км/ч), а скорость против течения х–1 (км/ч).
Расстояние и в ту, и в другую сторону одинаково и равно 15 км.
Всего время нахождения лодки в пути 10 часов (на весь путь: туда, 2 часа стоянка, обратно). То есть:
10 = (ПО ТЕЧЕНИЮ)+(СТОЯНКА)+(ПРОТИВ ТЕЧЕНИЯ)
Занесем скорость и расстояние в таблицу. Заполняем графу «время».
Время, затраченное на путь до пункта назначения 15/(х+1),
Время, затраченное на путь обратно (против течения) 15/(х–1).
Составляем уравнение:
Не забываем, что скорость величина положительная.
Таким образом, собственная скорость лодки в неподвижной воде будет 4 (км/ч).
Конечно, для моторной лодки такая скорость маловата в реальной жизни, но будем считать, что это старая лодка с изношенным еле работающем двигателем (шучу).
Ответ: 4
Решите самостоятельно:
Посмотрите решение
Что ещё хотелось бы добавить. Если в задачах, когда речь идёт о времени и сказано, что один участник движения затратил на столько-то часов больше (меньше), вы всё-таки, не можете понять, как записать выражение. Например, в первой рассмотренной задаче:
то есть, не можете определить — как и к чему прибавить (вычесть) двойку, то поступайте просто: ставьте любой знак и решайте.
В случае, если знак поставлен верно, задача решится. Если неверно, то вы получите отрицательный дискриминант при решении квадратного уравнения, то есть задача будет неразрешима. В этом случае просто меняйте знак на противоположный и всё, задача решится.
Я не призываю бездумно использовать данный подход всегда в подобных задачах. Это совет на случай, если вы в тупике при решении или на самом ЕГЭ запутались, всё-таки психологическая нагрузка.
На этом всё. На десерт позитивное видео.
Успехов Вам!
С уважением, Александр Крутицких.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
Тема: Задачи на движение по реке.
Цели:
- обобщить и систематизировать знания по теме
«Задачи на движение по реке»; - проверить знание теоретического материала,
умение решать задачи арифметическим способом; - развивать кругозор, мышление, внимание,
культуру математической речи; - прививать интерес к математике.
Методы обучения: частично-поисковый
(эвристический), системные обобщения,
самопроверка, взаимопроверка.
Формы организации урока: фронтальная,
индивидуальная.
Оборудование: презентация к уроку,
листы учета знаний.
ХОД УРОКА
I. Организационный момент
Сообщить учащимся цели урока. Настроить ребят
на активную работу.
II. Проверка домашнего задания
№ 391(а).
Собственная скорость теплохода 27км/ч, скорость
течения реки 3 км/ч. Сколько времени затратит
теплоход на путь по течению реки между двумя
причалами, если расстояние между ними 120 км?
Решение:
1) Vпо теч.= Vсоб.+ Vтеч. = 27 + 3 = 30 (км/ч).
2) tпо теч.= S : Vпо теч.= 120 : 30 = 4 (ч.)
Ответ: 4 часа.
№ 392.
Катер, имеющий собственную скорость 15 км/ч,
проплыл 2 часа по течению реки и 3часа против
течения. Какое расстояние проплыл катер за все
время, если скорость течения реки 2 км/ч?
Решение:
1) Vпо теч.= Vсоб. + Vтеч.= 15 + 2 = 17 (км/ч.)
2) Vпр. теч.= Vсоб. – Vтеч.= 15 – 2 = 13 (км/ч.)
3) Sпо теч.= Vпо теч. · tпо теч. = 17 · 2 = 34 (км)
4) Sпр теч.= Vпр. теч.· t пр. теч.=13 · 3 = 39 (км)
5) S=Sпо теч.+ Sпр. теч. = 34 + 39 = 73 (км)
Ответ: 73 км
III. Актуализация знаний
(Фронтальная работа)
Вопросы: (устно или с использованием
проектора.)
1. Что такое собственная скорость катера? Ответ:
скорость катера в стоячей воде (озере, пруду).
2. Что такое скорость течения? Ответ: на какое
расстояние относит река предмет за единицу
времени.
3. Как определяется скорость катера по течению
реки? Ответ: как сумма скорости собственной и
течения.
4. Как определяется скорость катера против
течения? Ответ: как разность скорости
собственной и течения.
5. Как определяется скорость движения плота по
реке? Ответ: как скорость течения реки.
Подведем итог:
Vпо течению – сумма V течения и V
собственной.
V против течения – разность Vсобственной и
Vтечения.
Значит, зная Vпо течению и Vпротив течения, можно
найти Vтечения и Vсобственной.
Вспомним задачу на нахождение двух чисел по их
сумме и разности.
1) (V по теч. – V пр. теч.) : 2 = Vтеч.
2) Vпо теч. – Vтеч. = Vсоб.
IV. Решение задач
№ 1.
Из четырех скоростей (Vсоб.,Vпо теч.,Vпр. теч.,Vтеч.
) две заданы и изображены отрезком. Вычислите две
другие скорости и изобразите их отрезками:
№ 2. Заполним таблицу.
|
Vсоб, км/ч |
V теч, км/ч |
Vпо теч, км/ч |
Vпр. теч, км/ч |
|
15 |
3 |
? |
? |
|
16 |
? |
18 |
? |
|
13 |
? |
? |
10 |
|
? |
2 |
11 |
? |
|
? |
3 |
? |
15 |
|
? |
? |
28 |
24 |
№ 3
Решим задачу № 393 (а).
Расстояние между двумя причалами 24 км. Сколько
времени потратит моторная лодка на путь от
одного причала до другого и обратно, если
собственная скорость моторной лодки 10 км/ч, а
скорость течения 2 км/ч?
Решение:
1) Vпо теч.= Vтеч.+ Vсоб.= 2 + 10 = 12 (км/ч)
2) Vпр. теч. = Vсоб. – Vтеч.= 10 – 2 = 8 (км/ч)
3) tпо теч.= S : Vпо теч.= 24 : 12 = 2 (ч)
4) tпр. теч.= S : Vпр. теч.= 24 : 8 = 3 (ч)
5) t = tпо теч. + tпр. теч.= 2 + 3 = 5 (ч)
Ответ: 5 часов.
V. Самостоятельная работа
|
I вариант |
II вариант |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1) Скорость моторной лодки в стоячей воде 15км/ч, а скорость течения реки 3 км/ч. Сколько времени потратит моторная лодка на путь от одной пристани до другой и обратно, если расстояние между пристанями 36 км? 2)
|
1) Скорость моторной лодки в стоячей воде 10 км/ч, а скорость течения реки 2 км/ч. Сколько времени потратит моторная лодка на движение от одной пристани до другой и обратно, если расстояние между пристанями 24 км? 2)
|
VI. Подведение итогов урока
Заполнить карточку самоанализа.
Объявление оценок за урок.
VII. Определение домашнего задания
№ 393 (б), 394 С.М.Никольский, М.К.Потапов,
Н.Н.Решетников, А.В.Шевкин. Математика:
учебник для 6 кл. общеобразовательных
учреждений.– М.: Просвещение, 2008 г.
Презентация
Список литературы:
1. С.М.Никольский, М.К.Потапов, Н.Н.Решетников,
А.В.Шевкин. Математика: учебник для 6 кл.
общеобразовательных учреждений. – М.:
Просвещение, 2008 г.
2. А.В.Шевкин. Обучение решению текстовых
задач в 5-6 классах. – М.: «Русское слово», 2001г.
Теплоход проходит от пристани А до пристани Б против течения реки за 10 часов, а по течению – за 6 часов. Найдите расстояние между пристанями А и Б, если скорость течения реки 2 км/ч. Ответ выразите в километрах.
Решение
Пусть (x) км/ч – скорость теплохода. Тогда, скорость теплохода по течению будет равна (x+2) км/ч, а против течения – (x-2) км/ч.
Расстояние находится по формуле (S=Vcdot t), где (V) – скорость, (t) – время.
Можно написать, что теплоход прошел из точки А в Б (против течения) ((x-2)cdot 10) км. А в обратном направлении из точки Б в А (по течение) теплоход прошел ((x+2)cdot 6) км.
Приравняем расстояния и найдем скорость теплохода:
((x-2)cdot10=(x+2)cdot 6;)
(10x-20=6x+12;)
(4x=32;)
(x=8).
Получилось, что скорость теплохода равна (8) км/ч. Найдем расстояние между пристанями А и Б:
((8-2)cdot 10=60) км.
Ответ: (60).
Источник: ЕГЭ 2023 Математика. Базовый уровень. Типовые экзаменационные варианты. 30 вариантов (вариант 7) (Купить книгу)
|
забыли пароль? Помощь сайту |
Решение задач по алгебре на движение по реке. Движение по течению и против течения. создана: 29.09.2019 в 19:36
liliana : В задачах на движение по реке учитывается скорость течения реки. Лодки, катера, баржи имеют собственную скорость. При движении по течению реки Иногда в задачах движение против течения реки называют «вверх по течению», При плавании по озеру лодки, катера и баржи движутся только с собственной скоростью
Хочу написать ответ |
Задачи на движение по реке
Рассмотрим задачи, в которых речь идёт о движении объекта по реке. Скорость любого объекта в стоячей воде называют собственной скоростью этого объекта.
Чтобы узнать скорость объекта, который движется против течения реки, надо из собственной скорости объекта вычесть скорость течения реки.
Задача 1. Катер движется против течения реки. За сколько часов он преодолеет расстояние 112 км, если его собственная скорость 30 км/ч, а скорость течения реки 2 км/ч?
Решение: Сначала узнаем скорость движения катера против течения реки, для этого от его собственной скорости отнимем скорость течения:
30 — 2 = 28 (км/ч) — скорость движения катера против течения.
Теперь можно узнать за сколько часов катер преодолеет 112 км, разделив расстояние на скорость:
112 : 28 = 4 (ч).
Решение задачи по действиям можно записать так:
1) 30 — 2 = 28 (км/ч) — скорость движения катера против течения,
2) 112 : 28 = 4 (ч).
Ответ: За 4 часа катер преодолеет расстояние 112 км.
Чтобы узнать скорость объекта, который движется по течению реки, надо к собственной скорости объекта прибавить скорость течения реки.
Задача 2. Расстояние от пункта A до пункта B по реке равно 120 км. Сколько времени потратит моторная лодка на путь от пункта A до B, если её собственная скорость 27 км/ч, а скорость течения реки 3 км/ч?
Рассмотрите два варианта:
1) лодка движется по течению реки;
2) лодка движется против течения реки.
Решение: Если моторная лодка будет двигаться по течению реки, то её скорость будет равна сумме собственной скорости со скоростью течения реки:
27 + 3 = 30 (км/ч).
Значит расстояние между пунктами лодка преодолеет за:
120 : 30 = 4 (ч).
Если лодка будет двигаться против течения реки, то её скорость будет равна разности собственной скорости и скорости течения реки:
27 — 3 = 24 (км/ч).
Значит, чтобы узнать сколько времени потратит лодка на путь от пункта A до пункта B, надо расстояние разделить на скорость:
120 : 24 = 5 (ч).
Решение задачи по действиям для движения по течению реки можно записать так:
1) 27 + 3 = 30 (км/ч) — скорость лодки,
2) 120 : 30 = 4 (ч).
Для движения против течения реки решение задачи по действиям можно записать так:
1) 27 — 3 = 24 (км/ч) — скорость лодки,
2) 120 : 24 = 5 (ч).
Ответ:
1) При движении по течению реки моторная лодка потратит 4 часа на путь от пункта A до пункта B.
2) При движении против течения реки моторная лодка потратит 5 часов на путь от пункта A до пункта B.