- Подробности
- Обновлено 03.07.2018 18:27
- Просмотров: 689
Задачи по физике — это просто!
Не забываем, что решать задачи надо всегда в системе СИ!
А теперь к задачам!
Элементарные задачи из курса школьной физики по кинематике.
Задача на определение расстояния между двумя телами при прямолинейном равномерном движении
Смысл задачи:
Два тела движутся навстречу друг другу. Даны их начальные координаты и перемещения за одинаковый отрезок времени после начала движения. Определить расстояние между телами через какое-то время после начала движения.
Условия задачи:
Два автобуса движутся вдоль прямого шоссе навстречу друг другу. Они одновременно отошли от остановок, находящихся на расстоянии 200 м и 600 м от моста. Определить расстояние между ними, если за одинаковое время один прошел 50 м, а другой — 100 м.
Выбираем мост за точку отсчета. Т.к. движение по прямой, выбираем одномерную систему координат — ось ОХ.
На координатной оси от точки отсчета откладываем начальные координаты хo1 и хо2.
Из начальных координат показываем вектора перемещения, направленные навстречу друг другу (желательно, чтобы на чертеже соотношение длин векторов перемещения для наглядности соответствовала условиям задачи).
Ставим точки, соответствующие конечным координатам тел — х1 и х2. Расстояние между этими точками (х1 и х2) и требуется определить.
Для каждого тела записываем расчетную формулу для определения координаты при прямолинейном равномерном движении и делаем расчет.
Не забываем, что проекция перемещения для вектора Sx2, направленного противоположно координатной оси, отрицательна, поэтому (-100 м) в расчете.
Формула для расчета расстояния l очень удобна. Она дает абсолютное значение разности, поэтому безразлично, где эти координаты находятся на оси, и из какой координаты какую вычитать
.
Любознательным
Сбивание и нагревание яичных белков
Почему при сбивании яичные белки из жидкости превращаются в густую пену?
Почему взбивание делает белок таким плотным?
Почему яичный белок, сначала — прозрачная бесцветная жидкость, превращается в почти твердое вещество, когда вы жарите яичницу?
Оказывается…
Молекулы в яичном белке запутаны, как макароны. Когда белок сбивают или нагревают, молекулы расправляются
и начинают сильнее притягивать друг друга, поэтому белок становится жестче.
Источник: «Физический фейерверк» Дж. Уокер
Кинематика
Динамика
- Силы трения
- Трение покоя
Максимальная сила трения покоя (Fтр)max пропорциональна силе нормального давления (N) и зависит от характера взаимодействия соприкасающихся поверхностей тел, определяемого коэффициентом трения (μ)
(Fтр)max=μ×N
СИ: Н - Трение скольжения
Сила трения скольжения (Fтр) пропорциональна силе давления (N), коэффициенту трения (μ) и направлена противоположно направлению движения тела.
Fтр=μ×N
СИ: Н - Коэффициент трения
Коэффициент трения (μ) вычисляют как отношение модулей силы трения (Fтр) и силы давления (N).
μ=Fтр/N - Движение тела под действием силы трения
1) Путь (l), пройденный движущимся телом под действием силы трения до полной остановки (тормозной путь), прямо пропорционален квадрату начальной скорости (v0) и обратно пропорционален коэффициенту трения (μ):
, (g — ускорение свободного падения).
2) Время (t) движения тела под действием силы трения до момента полной остановки (время торможения) прямо пропорционально начальной скорости (v0) и обратно пропорционально коэффициенту трения (μ):
СИ: м, с
, (g — ускорение свободного падения).
- Движение тела под действием нескольких сил
- Условие равновесия тела (как материальной точки).
Тело находится в равновесии (в покое или движется равномерно и прямолинейно), если сумма проекций всех сил (), действующих на тело, на любую ось (ОХ, ОY, O, …) равна нулю.
;
;
СИ: Н - Движение тела по наклонной плоскости
Ускорение тела, скользящего вниз по наклонной плоскости с углом наклона (α) и коэффициентом трения тела о плоскость (μ), не зависит от массы тела и равно:, (g — ускорение свободного падения)
СИ: м/с2 - Движение связанных тел через неподвижный блок
Ускорение двух тел, массами m1 и m2, связанных нитью, перекинутой через неподвижный блок, равно:
, (g — ускорение свободного падения)
СИ: м/с2
), действующих на тело, на любую ось (ОХ, ОY, O, …) равна нулю.
;
;
, (g — ускорение свободного падения)
, (g — ускорение свободного падения)- Законы сохранения в механике
- Импульс тела
Импульс тела () — векторная величина, равная произведению массы (m) тела на его скорость ().
СИ: (кг×м)/с - Импульс силы
Импульс силы ( — произведение силы на время t её действия) равен изменению импульса тела.
СИ: Н×с - Закон сохранения импульса
Геометрическая сумма импульсов тел (), составляющих замкнутую систему, остается постоянной при любых движениях и взаимодействиях тел системы.
СИ: Н×с - Механическая работа силы
Работа (А) постоянной силы равна произведению модулей векторов силы () и перемещения () на косинус угла между этими векторами.
СИ: Дж - Теорема о кинетической энергии
Работа (А) силы (или равнодействующей сил) равна изменению кинетической энергии (Ek1 и Ek2) движущегося тела.
,
где m — масса тела, v1, v2 — начальная и конечная скорости тела
СИ: Дж - Потенциальная энергия поднятого тела
Потенциальная энергия (ЕП) тела, поднятого на некоторую высоту (h) над нулевым уровнем, равна работе (А) силы тяжести (m×g) при падении тела с этой высоты до нулевого уровня.
A=ЕП=m×g×h
СИ: Дж - Работа силы тяжести
Работа (А) силы тяжести (mg) не зависит от пути, пройденного телом, а определяется разностью высот (Δh=h2-h1) положения тела в конце и в начале пути и равна разности его потенциальных энергий (EП2 и EП1).
A=-(EП2-EП1)=-m×g×Δh
СИ: Дж - Потенциальная энергия деформированного тела
Потенциальная энергия (ЕП) деформированного тела (пружины) равна работе силы упругости при переходе тела (пружины) в состояние, в котором его деформация равна нулю.
ЕП =,
где k — жесткость; х — деформация пружины.
СИ: Дж - Закон сохранения полной механической энергии
Полная механическая энергия замкнутой системы тел, взаимодействующих силами тяготения или силами упругости, остается неизменной при любых движениях тел системы.
ЕК2+ЕП2=ЕК1+ЕП1=const
СИ: Дж
) — векторная величина, равная произведению массы (m) тела на его скорость (
).
— произведение силы 
на время t её действия) равен изменению импульса тела.
), составляющих замкнутую систему, остается постоянной при любых движениях и взаимодействиях тел системы.
) на косинус угла между этими векторами.
,
,- Движение жидкостей и газов по трубам
- Закон Бернулли
Давление жидкости, текущей в трубе, больше в тех частях трубы, где скорость её движения меньше, и наоборот, в тех частях, где скорость больше, давление меньше.
,
где p1, v1, h1 — давление, скорость и вертикальная координата жидкости в одном сечении трубы; p2, v2, h2 — давление, скорость и вертикальная координата жидкости в другом сечении трубы;
ρ — плотность жидкости; g — ускорение свободного падения.
СИ: Па
,
Скорость равномерного прямолинейного движения прямо пропорциональна перемещению тела и обратно пропорциональна значению времени этого перемещения.
v→=s→t.
Можно выразить перемещение из этой формулы, умножив обе части на значение времени: s→=v→⋅t.
О направлении векторов этих величин относительно друг друга можно судить, в частности, по уравнениям, записанным в векторной форме.
Проекция перемещения на ось (OX) рассчитывается по формуле
sx=vxt
, где (upsilon_x) — проекция скорости на ось (OX) принимает положительное значение, если направление перемещения совпадает с направлением оси (OX); принимает отрицательное значение, если перемещение противоположно направлено относительно оси (OX).
Если при решении задач направление движения не влияет на смысл условия и ход решения задачи, то направление векторных величин можно не учитывать. Тогда говорят о модулях величин, то есть их размере без учёта направления: (|vec{s}|=|vec{upsilon}|cdot t) можно заменить на s=vt.
При прямолинейном равномерном движении модуль перемещения равен пройденному пути: (|vec{s}|=s), если направление скорости совпадает с направлением вектора перемещения.
На рисунке представлена зависимость (v(t)) для равномерного движения.
Формула для расчета модуля перемещения: s=v1⋅t1.
Однако произведение v1⋅t1, т.е. скорости на промежуток времени, численно равно площади (S) закрашенной фигуры (в данном случае прямоугольника).
Это наблюдение позволяет сделать вывод; что при прямолинейном равномерном движении модуль перемещения численно равен площади прямоугольника, которые образуется между графиком скорости и осью времени. При этом необходимо учитывать моменты времени: начало наблюдения за объектом и конец наблюдения. В данном случае начало наблюдения соответствует точке (O,) а конец наблюдения — точке t1.
Можно говорить о равенстве пройденного пути и площади под графиком скорости.
Понятие о времени
Существует характеристика, с которой приходится сталкиваться каждый день вне зависимости от возраста, социального статуса, различных способностей и умений. С её помощью определяют будущее, прошедшее и настоящее. По сути, это маркер, определяющий событие. Называют его временем. Рассматривая движение, всегда учитывают эту характеристику, как и её прогрессию.
Время является частью пространственной координаты. Но если относительно других осей можно перемещаться в различных направлениях, относительно него движение определяется только вперёд или назад. Неотъемлемой частью, связанной со временем, является пространство, благодаря которому и возможно понять суть параметра.
Исследованием характеристики занимались философы и учёные в различные периоды существования человечества. Видеть и слышать время невозможно, в отличие от осязаемого пространства, которое возможно наблюдать сразу и везде. Причём в нём можно перемещаться.
Дискуссии, как правильно воспринимать время, не утихают до сих пор. Платон считал, что оно есть не что иное, как движение. Аристотель предполагал, что время — количественное измерение перемещения. Оно было добавлено к классической геометрии Евклида, действующей на ограниченное число измерений. В итоге стало рассматриваться четырёхмерное пространство.
Сегодня так и нет ответов на следующие вопросы о времени:
- из-за чего происходит его течение;
- почему оно определяется только в одном направлении;
- является ли параметр одномерным, как многие учёные считают;
- можно ли обнаружить кванты характеристики.
В классической физике для определения временного изменения используется специальная координата пространство-время. Принято будущие события обозначать знаком плюс, а прошедшие минусом. Единица измерения времени связана с вращением планеты вокруг своей оси и Солнца. Этот выбор был сделан условно и привязан к удобству жизнедеятельности человечества.
В Международной системе единиц принято за секунду принимать интервал, равный 9 192 631 770 периодам излучения атома цезия-133 в покое при нуле градусов по Кельвину. Обозначают параметр латинской буквой t. Таким образом, время — физическая величина, связанная с перемещением какого-либо тела относительно выбранной системы координат.
Расстояние и скорость
Положение каждой физической точки можно описать с помощью координатных осей. Другими словами, системой, которая по отношению к исследуемому телу остаётся неизменной. Изменение положения относительно другого объекта можно представить пройденным расстоянием. Фактически это путь, для которого известно начало и конец. С физической точки зрения, расстояние — величина, являющаяся размерностью длины, и выражающаяся в её единицах.
В математике мера пройденного пути тесно связана с метрическим пространством, то есть положением, где существует пара (x, d), определённая в декартовом произведении. Соответственно, если координату принять за x, y, можно сказать следующее:
- начало пути и его конец обозначают точками с координатами d (x, y) и p (x, y);
- пройденное расстояние можно определить, отняв из конечных координат начальные;
- изменение положения будет нулевым, когда d = p.
В физике расстояние измеряют единицами длины. В соответствии с СИ за размерность берут метр. Расстояние — мера пройденного пути, то есть длина. Если необходимо просто определить изменение положения без учёта, когда и как оно произошло, используют координатные оси. Но при нахождении пройденного пути за время в формуле для расстояния должна учитываться ещё одна величина — скорость.
Обозначают эту характеристику символом V. Характеризует она быстроту перемещения в выбранной системе отсчёта. По определению скорость равняется производной радиус-вектора точки по времени. Иными словами, это значение, задающееся положением в пространстве относительно неизменной координаты, за которую чаще всего принимается начало.
Одно и то же расстояние можно преодолеть за разное время. Например, чтобы пройти 7 километров человеку понадобится затратить порядка одного часа, на автомобиле же этот путь можно преодолеть за 10 минут, а то и меньше. Вот как раз эти отличия и зависят от скорости движения.
Но на самом деле не всё так однозначно. Скорость необязательно должна быть одинаковой на всём пути. На определённых промежутках она может увеличиваться или уменьшаться, поэтому в математике под её значением понимают среднюю величину. Считается, что тело движется равномерно при прохождении установленного расстояния.
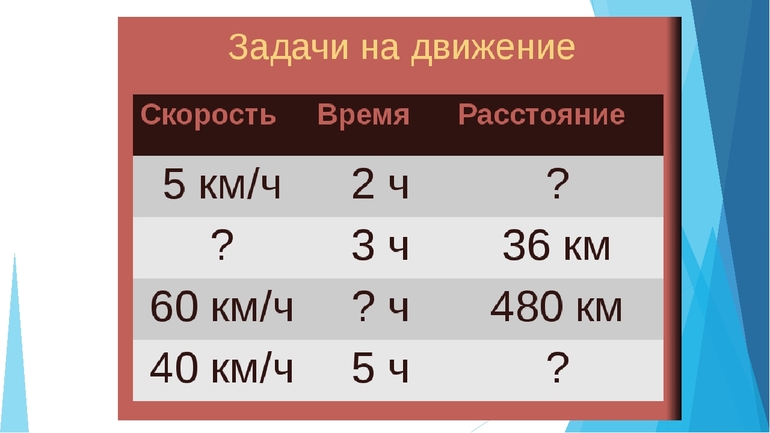
Общая формула
Скорость, время, расстояние — это 3 фундаментальных величины, связанные друг с другом. Исследуя одну характеристику, обязательно нужно учитывать две других. Фактически скорость — это физическая величина, определяющая, какую длину преодолеет физическое тело за единицу времени. Например, значение 120 км/ч показывает, что объект сможет преодолеть 120 километров за один час. В математическом виде связь между тремя характеристиками может быть записана в виде следующей формулы:
S = V * t, где:
- S — пройденное объектом расстояние;
- V — средняя скорость тела;
- t — время, затраченное на преодоление пути.
Зная это равенство и любых 2 параметра, можно выполнить расчёт третьего, так для времени она будет иметь вид t = S / V, а скорости V = S / t. Проверить правильность формулы для скорости времени и расстояния можно путём анализа размерности. Если в выражение подставить единицы измерения, то после сокращения должна получиться величина, соответствующая определяемой. S = V * t = (м / с) * с = м (метр). Что и требовалось получить. Аналогично можно проверить и 2 оставшиеся формулы: t = s / v = м / (м/с) = м * с / м = с (секунда) и V = S / t = м / с (метр на секунду).
Действительно, пусть имеется физическое тело, находящееся в каком-то месте. Через некоторое время, неважно по каким причинам, оно переместилось в другую точку, при этом не выходя за пределы установленного пространства. Если тело представить в декартовой плоскости, причём за начало принять координату (0, 0), через время объект изменит своё положение, определяющееся значением (x1, y2). В двухмерном же пространстве это изменение можно описать как переход из точки A в Б.
Значит, чтобы тело достигло второй координаты, ему необходимо затратить время. При этом пройденный путь будет находиться в прямой зависимости от него. Расстояние и время должны связываться третьей величиной, которой как раз и является скорость. То есть параметр, определяющий, за сколько тело сможет преодолеть определённую длину.
Как видно, выражение, связывающее 3 величины, довольно простое. Но оно не учитывает, что скорость может быть непостоянной, поэтому если объект проходит свой путь неравномерно, в выражение подставляют среднее значение. Находится оно как сумма всех отдельных скоростей на неравномерных участках: Vср = ΔS / Δt.
Решение задач
Чтобы уметь решать простые задания в средних классах по математике, связанных с движением, нужно знать всего одну формулу. При этом необходимо пристальное внимание уделять размерности. Все вычисления осуществляются в СИ. Вот некоторые из типовых заданий, используемые при обучении школьников в четвёртом классе средней школы:
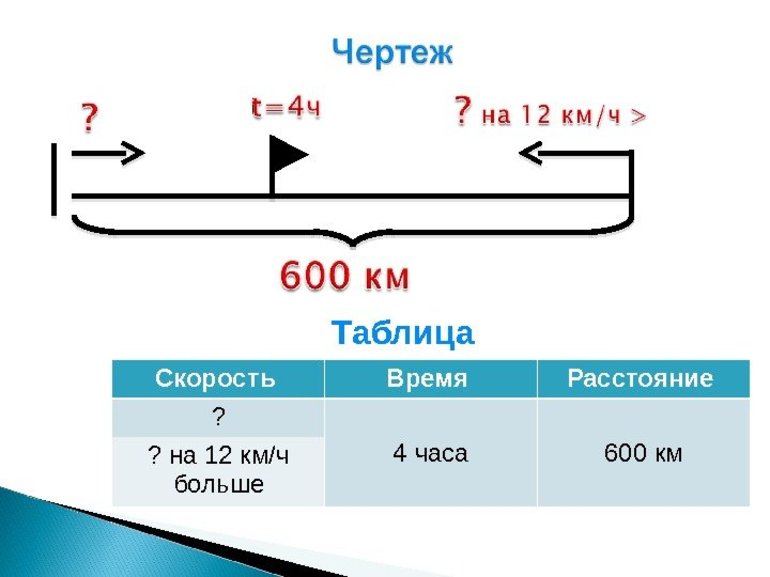
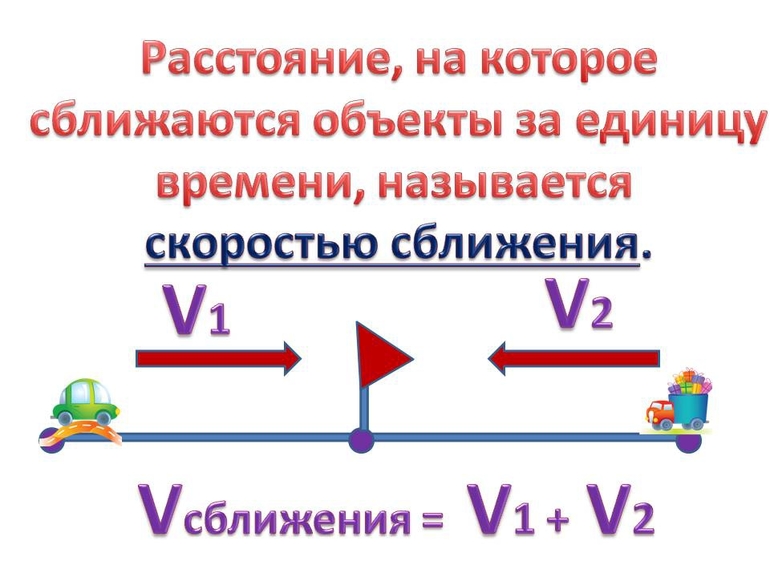
- Из населённого пункта А в точку Б выехала колонна грузовиков. Навстречу им отправился легковой автомобиль. Скорость грузоперевозчиков составляет 80 км/ч, а пассажирской машины 60 км/ч. Встретились они в точке C через полтора часа. Определить расстояние между А и Б. Решение этой задачи будет состоять из нескольких шагов. На первом можно найти путь, который проехала колона: 80 * 1,2 = 96 км. На втором вычислить пройденное расстояние второй: 60 * 1,2 = 72 км. Отсюда общий путь будет равен сумме: АС + СБ = 72 + 96 = 168 км.
- Корабль, скорость которого в стоячих водах равна 30 км/ч, идёт по течению, а после возвращается. Скорость реки равняется трём километрам в час, промежуточная остановка занимает 5 часов. Путь от начала до возврата корабль проходит за 30 часов. Найти, сколько километров составляет весь рейс. Чтобы решить задачу, удобно составить таблицу. В столбцах нужно записать расстояние, скорость и время, а в строках расчётные данные для таких событий, как стоянка, ход по и против течения. Учитывая условие, рабочая формула примет вид: (S / 28) + (S / 22) + 5 = 30. Выражение можно упростить. В итоге должно получиться: 25 * S / 308 = 25 → S = 308. Так как путь корабля состоял из двух одинаковых расстояний, искомое расстояние будет: P = 2 * S = 308 * 2 = 616 км.
- Железнодорожный состав проезжает мост за 45 секунд. Длина переправы составляет 450 метров. При этом стрелочник, смотря прямо, видит проходящий поезд всего 15 секунд. Найти длину состава и скорость его движения. Если принять, что поезд движется со скоростью V, то его длина будет равняться D = 15 * V. Так как состав за 45 секунд проходит расстояние 45 * V = 450 + 15 * V, из равенства легко определить скорость: V = 45 * V – 15 * V = 450 → V = 450 / 3 0 = 15 м / с. Следовательно, длина состава: D = 15 * 15 = 225 м.
Все задачи на движение можно разделить на несколько типов: перемещение навстречу, движение вдогонку, нахождение параметров относительно неподвижного объекта. Но, несмотря на их виды, все они решаются по одинаковому алгоритму, поэтому для удобства можно сделать памятку, указав в ней формулы и размерность величин.