Пересечение двух окружностей
Этот онлайн калькулятор находит точки пересечения двух окружностей, если они существуют
Чтобы использовать калькулятор, введите координаты x и y центра и радиус каждой окружности.
Формулы для расчета приведены под калькулятором.
Точки пересечения двух окружностей
Первая окружность
Вторая окружность
Пересечение окружностей
Сама по себе задача нахождения точек пересечения двух окружностей достаточно проста, однако предварительно надо проанализировать если ли вообще точки пересения у данных двух окружностей. Поэтому начать надо с вычисления расстояния d в декартовых координатах между центрами окружностей и сравнения его с радиусами окружностей r1 и r2.
При этом возможно следующие случаи (расстояние между центрами показано красным отрезком):
| Случай | Описание | Условие |
|---|---|---|
| Тривиальный случай — окружности совпадают (это одна и та же окружность) | ||
| Окружности не касаются друг друга | r1 + r2″ /> | |
| Одна окружность содержится внутри другой и не касается ее | ||
| Окружности пересекаются в двух точках | Не выполнено ни одно из условий выше | |
| Окружности соприкасаются в одной точке | Частный случай предыдущего |
Если окружности действительно пересекаются, калькулятор использует следующие формулы (в-основном выведенные из теоремы Пифагора), проиллюстрированные рисунком ниже:
Сначала калькулятор находит отрезок a
Чтобы найти точку P3, калькулятор использует следующую формулу (в векторном виде):
И наконец, чтобы найти точки пересечения, калькулятор использует следующие уравнения:
Первая точка:
Обратите внимание на разные знаки перед вторым слагаемым
По теме также можно посмотреть следующие ссылки (на английском языке): Circle-Circle Intersection и Circles and spheres
Вычислительная геометрия, или как я стал заниматься олимпиадным программированием. Часть 2
Вступление
Это вторая часть моей статьи посвящена вычислительной геометрии. Думаю, эта статья будет интереснее предыдущей, поскольку задачки будут чуть сложнее.
Начнем с взаимного расположения точки относительно прямой, луча и отрезка.
Задача №1
Определить взаимное расположении точки и прямой: лежит выше прямой, на прямой, под прямой.
Решение
Понятно, что если прямая задана своим уравнением ax + by + c = 0, то тут и решать нечего. Достаточно подставить координаты точки в уравнение прямой и проверить чему оно равно. Если больше нуля, то точка находится в верхней полуплоскости, если равна нулю, то точка находится на прямой и если меньше нуля, то точка находится в нижней полуплоскости. Интереснее случай, когда прямая задана, задана координатами двух точек назовем их P1(x1, y1), P2(x2, y2). В этом случае можно спокойно найти коэффициенты a, b и c и применить предыдущее рассуждение. Но надо сначала подумать, оно нам надо? Конечно, нет! Как я говорил косое произведения — это просто жемчужина вычислительной геометрии. Давайте применим его. Известно, что косое произведение двух векторов положительно, если поворот от первого вектора ко второму идет против часовой стрелки, равно нулю, если векторы коллинеарны и отрицательно, если поворот идет по часовой стрелки. Поэтому нам достаточно посчитать косое произведение векторов P1P2 и P1M и по его знаку сделать вывод.
Задача №2
Определить принадлежит ли точка лучу.
Решение
Давайте вспомним, что такое луч: луч — это прямая, ограниченная точкой с одной стороны, а с другой стороны бесконечная. То есть луч задается некоторой начальной точкой и любой точкой лежащей на нем. Пусть точка P1(x1, y1) — начало луча, а P2(x2, y2) — любая точка принадлежащая лучу. Понятно, что если точка принадлежит лучу, то она принадлежит и прямой проходящей через эти точки, но не наоборот. Поэтому принадлежность прямой является необходимым, но не достаточным условием для принадлежности лучу. Поэтому от проверки косового произведения нам никуда не деться. Для достаточного условия нужно вычислить еще и скалярное произведение тех же векторов. Если оно меньше нуля, то точка не принадлежит лучу, если же оно не отрицательно, то точка лежит на луче. Почему так? Давайте посмотрим на рисунок.
Итак, для того чтобы точка M(x, y) лежала на луче с начальной точкой P1(x1, y1), где P2(x2, y2) лежит на луче необходимо и достаточно выполнения двух условий:
1. [P1P2, P1M] = 0 – косое произведение (точка лежит на прямой)
2. (P1P2, P1M) ≥ 0 – скалярное произведение (точка лежит на луче)
Задача №3
Определить принадлежит ли точка отрезку.
Решение
Пусть точки P1(x1, y1), P2(x2, y2) концы заданного отрезка. Опять-таки необходимым условием принадлежности точки отрезку является ее принадлежность прямой проходящей через P1, P2. Далее нам нужно определить лежит ли точка между точками P1 и P2, для этого нам на помощь приходит скалярное произведение векторов только на этот раз других: (MP1, MP2). Если оно меньше либо равно нуля, то точка лежит на отрезке, иначе вне отрезка. Почему так? Посмотрим на рисунок.
Итак, для того чтобы точка M(x, y) лежала на отрезке с концами P1(x1, y1), P2(x2, y2) необходимо и достаточно выполнения условий:
1. [P1P2, P1M] = 0 – косое произведение (точка лежит на прямой)
2. (MP1,MP2) ≤ 0 – скалярное произведение (точка лежит между P1 и P2)
Задача №4
Взаимное расположение двух точек относительно прямой.
Решение
В этой задаче необходимо определить по одну или по разные стороны относительно прямой находятся две точки.
Если точки находятся по разные стороны относительно прямой, то косые произведения имеют разные знаки, а значит их произведение отрицательно. Если же точки лежат по одну сторону относительно прямой, то знаки косых произведений совпадают, значит, их произведение положительно.
Итак:
1. [P1P2, P1M1] * [P1P2, P1M2] 0 – точки лежат по одну сторону.
3. [P1P2, P1M1] * [P1P2, P1M2] = 0 – одна (или две) из точек лежит на прямой.
Кстати, задача об определении наличия точки пересечения у прямой и отрезка решается точно также. Точнее, это и есть эта же задача: отрезок и прямая пересекаются, когда концы отрезка находятся по разные стороны относительно прямой или когда концы отрезка лежат на прямой, то есть необходимо потребовать [P1P2, P1M1] * [P1P2, P1M2] ≤ 0.
Задача №5
Определить пересекаются ли две прямые.
Решение
Будем считать, что прямые не совпадают. Понятно, что прямые не пересекаются, только если они параллельны. Поэтому, найдя условие параллельности, мы можем, определить пересекаются ли прямые.
Допустим прямые заданы своими уравнениями a1x + b1y + c1 = 0 и a2x + b2y + c2 = 0. Тогда условие параллельности прямых заключается в том, что a1b2 — a2b1 = 0.
Если же прямые заданы точками P1(x1, y1), P2(x2, y2), M1(x3, y3), M2(x4, y4), то условие их параллельности заключается в проверки косого произведения векторов P1P2 и M1M2: если оно равно нулю, то прямые параллельны.
В общем, то когда прямые заданы своими уравнениями мы тоже проверяем косое произведение векторов (-b1, a1), (-b2, a2) которые называются направляющими векторами.
Задача №6
Определить пересекаются ли два отрезка.
Решение
Вот эта задача мне, действительно, нравится. Отрезки пересекаются тогда, когда, концы каждого отрезка лежат по разные стороны от другого отрезка. Посмотрим на рисунок:
Итак, нам нужно проверить, чтобы концы каждого из отрезков лежали по разные стороны относительного концов другого отрезка. Пользуемся косым произведением векторов. Посмотрите на первый рисунок: [P1P2, P1M2] > 0, [P1P2, P1M1] [P1P2, P1M2] * [P1P2, P1M1] 2 + b 2 ).
Задача №8
Расстояние от точки до луча.
Решение
Эта задача отличается от предыдущей тем, что в этом случае может получиться, так что перпендикуляр из точки не падает на луч, а падает на его продолжение.
В случае, когда перпендикуляр не падает на луч необходимо найти расстояние от точки до начала луча – это и будет ответом на задачу.
Как же определить падает ли перпендикуляр на луч или нет? Если перпендикуляр не падает на луч, то угол MP1P2 – тупой иначе острый (прямой). Поэтому по знаку скалярного произведения векторов мы можем определить попадает ли перпендикуляр на луч или нет:
1. (P1M, P1P2) 2 .
Теперь рассмотрим случай, когда центр второго круга O2 находится между точками O1 и C. В этом случае получим отрицательное значение величины d2. Использование отрицательного значения d2 приводит к отрицательному значению α. В этом случае необходимо для правильного ответа прибавить к α 2π.
Заключение
Ну вот и все. Мы рассмотрели не все, но наиболее часто встречаемые задачи вычислительной геометрии касающиеся взаимного расположения объектов.
Расстояние между двумя точками онлайн
С помощю этого онлайн калькулятора можно найти расстояние между точками по известным координатам этих точек. Дается решение с пояснениями. Для нахождения расстояния между точками задайте размерность (2-если задача рассматривается в двухмерном пространстве, 3- если задача рассматривается в трехмерном пространстве), введите координаты точек в ячейки и нажмите на кнопку «Решить». Теоретическую часть смотрите ниже.
Предупреждение
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Расстояние между двумя точками на прямой
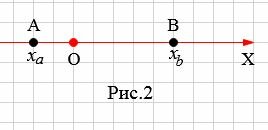
Пусть заданы на оси OX точки A с координатой xa и B с координатой xb (Рис.1). Найдем расстояние между точками A и B.
Расстояние между точками A и В равно:
| ( small AB=OB-OA. ) | (1) |
Поскольку расстояние от O до В равна xb, а расстояние от O до A равна xa, получим:
| ( small AB=x_b-x_a . ) | (2) |
На рисунке 2 точки A и В находятся по разные стороны начала координат O. B этом случае рассояние между точками A и B равно:
| ( small AB=OB+OA. ) | (3) |
Поскольку координата точки A отрицательна а координата точки B положительна, то (2) можно записать так:
| ( small AB=x_b+|x_a|=x_b-x_a . ) | (4) |
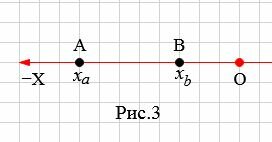
На рисунке 3 точки A и В находятся c левой стороны начала координат O.
B этом случае рассояние между точками A и B равно:
| ( small AB=OA-OB. ) | (5) |
Координаты точек A и B отрицательны. Тогда , то (5) можно записать так:
| ( small AB=|x_a|-|x_b|=x_b-x_a . ) | (6) |
Из формул (2),(4),(6) следует, что независимо от расположения точек отностительно начала координат рассояние этих точек равна разности координат этих точек, причем от большего значения вычитается меньшее (так как расстояние не может быть отрицательным числом).
Формулы (2),(4),(6) можно записать и так:
| ( small AB=|x_b-x_a|= |x_a-x_b| . ) | (7) |
Пример 1. на оси Ox заданы точки ( small A(x_a)=A(-4) ) и ( small B(x_b)=B(7) ) . Найти рассояние между этими точками.
Решение. Для нахождения расстояния между точками A и B воспользуемся формулой (7):
| ( small AB=|x_b-x_a|= |7-(-4)|=11 . ) | (7) |
Расстояние между двумя точками на плоскости
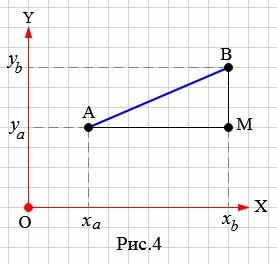
Пусть на плоскости задана декартова прямоугольная система координат XOY и пусть на плоскости заданы точки A и B, где A имеет координаты (xa,ya), а B имеет координаты (xb,yb) (Рис.4).
Учитывая результаты предыдующего параграфа, можем найти расстояние между точками A и M, а также расстояние между точками B и M:
| ( small AM=x_b-x_a,;; BM=y_b-y_a. ) | (8) |
ABM является прямоугольным треугольником, где AB гипотенуза, а AM и BM катеты. Тогда, исходя из теоремы Пифагора, имеем:
( small AB^2=AM^2+BM^2. )
Тогда, учитывая (8), получим:
( small AB^2=AM^2+BM^2=(x_b-x_a)^2+(y_b-y_a)^2. )
| ( small AB=sqrt <(x_b-x_a)^2+(y_b-y_a)^2>. ) | (9) |
Пример 2. На плоскости, в декартовой прямоугольной системе координат XOY заданы точки ( small A(x_a; y_a)=A(-6;3) ) и ( small B(x_b, y_b)=B(11,-4). ) . Найти рассояние между этими точками.
Решение. Для нахождения расстояния между точками A и B воспользуемся формулой (9). Подставляя координаты точек A и B в формулу (9), получим:

Ответ: 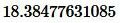
Расстояние между двумя точками в пространстве
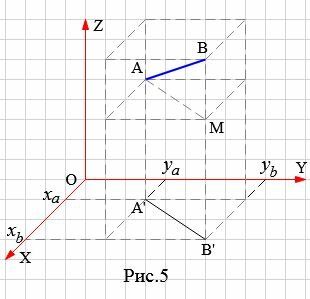
Рассмотрим в пространстве, в декартовой прямоугольной системе координат точки A и B, где A имеет координаты (xa,ya,za), а B имеет координаты (xb,yb,zb) (Рис.5).
AB является диагональю параллелепипеда, грани которго параллельны координатным плоскостьям и проходят через точки A и B. Но AB является гипотенузой прямоугольного треугольника AMB, а AM и BM являются катетами этого прямоугольного треугольника. Тогда, по теореме Пифагора, имеем:
| ( small AB^2=AM^2+BM^2. ) | (10) |
Учитывая, что BM равно разности третьих координат точек B и A, получим:
Из предыдующего параграфа следует, что:
| ( small A’B’^2=(x_b-x_a)^2+(y_b-y_a)^2. ) | (11) |
Но AM=A’B’. Тогда из (10) и (11) следует:
( small AB^2=AM^2+BM^2=A’B’^2+BM^2 ) ( small =(x_b-x_a)^2+(y_b-y_a)^2+(z_b-z_a)^2. )
| ( small AB= sqrt<(x_b-x_a)^2+(y_b-y_a)^2+(z_b-z_a)^2>. ) | (12) |
Пример 3. В пространстве задана декартова прямоугольная система координат XOY и точки ( small A(x_a; y_a ; z_a)=A(5;1;0) ) и ( small B(x_b, y_b, z_b)=B(-8,-4;21). ) Найти рассояние между этими точками.
Решение. Для нахождения расстояния между точками A и B воспользуемся формулой (12). Подставляя координаты точек A и B в формулу (12), получим:

Ответ: 
http://habr.com/ru/post/148325/
http://matworld.ru/analytic-geometry/rasstoyanie-mezhdu-dvumya-tochkami.php
Чтобы использовать калькулятор, введите координаты x и y центра и радиус каждой окружности.
Формулы для расчета приведены под калькулятором.
Точки пересечения двух окружностей
Первая окружность
Вторая окружность
Точность вычисления
Знаков после запятой: 2
Проверка расстояния между окружностями
Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.
Пересечение окружностей
Сама по себе задача нахождения точек пересечения двух окружностей достаточно проста, однако предварительно надо проанализировать если ли вообще точки пересения у данных двух окружностей. Поэтому начать надо с вычисления расстояния d в декартовых координатах между центрами окружностей и сравнения его с радиусами окружностей r1 и r2.
При этом возможно следующие случаи (расстояние между центрами показано красным отрезком):
| Случай | Описание | Условие |
|---|---|---|
| Тривиальный случай — окружности совпадают (это одна и та же окружность) | ||
 |
Окружности не касаются друг друга | |
 |
Одна окружность содержится внутри другой и не касается ее | |
  |
Окружности пересекаются в двух точках | Не выполнено ни одно из условий выше |
  |
Окружности соприкасаются в одной точке | Частный случай предыдущего |
Если окружности действительно пересекаются, калькулятор использует следующие формулы (в-основном выведенные из теоремы Пифагора), проиллюстрированные рисунком ниже:
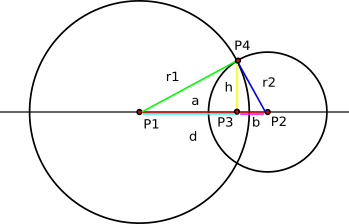
Сначала калькулятор находит отрезок a
и затем отрезок h
Чтобы найти точку P3, калькулятор использует следующую формулу (в векторном виде):
И наконец, чтобы найти точки пересечения, калькулятор использует следующие уравнения:
Первая точка:
Вторая точка:
Обратите внимание на разные знаки перед вторым слагаемым
По теме также можно посмотреть следующие ссылки (на английском языке): Circle-Circle Intersection и Circles and spheres
в каждом из следующих случаев: 385.1 центр окружности
совпадает с началом координат и ее радиус R=3; 385.2 центр окружности
совпадает с точкой С(2; -3) и ее радиус R=7; 385.3 окружность
проходит через начало координат и ее центр
совпадает с точкой С(6; -8); 385.4 окружность
проходит через точку А(2; 6) и ее центр совпадает с
точкой С(-1; 2); 385.5 точки А(3; 2) и В(-1; 6)
являются концами одного из диаметров окружности; 385.6 центр окружности
совпадает с началом координат и прямая
совпадает с точкой С(1; -1) и прямая
касательной к окружности; 385.8 окружность
проходит через точки А(3; 1) и В(-1; 3), а ее центр
лежит на прямой
проходит через три точки А(1; 1), В(1; -1), С(2; 0); 385.10 окружность
проходит через три точки: М1(-1;
5), М2(-2; -2). М3(5; 5). 386 Точка С(3; -1)
является центром окружности, отсекающей на
прямой
6. Составить уравнение этой окружности. 387 Написать уравнения
окружностей радиуса
прямой
уравнение окружности, касающейся прямых
одна из них – в точке А(2; 1). 389 Составить
уравнения окружностей, которые проходят через
точку А(1; 0) и касаются прямых
уравнение окружности, которая, имея центр на
прямой
касается прямых
уравнения окружностей, касающихся прямых
одной из них – в точке М1(1; 2). 392 Составить
уравнения окружностей, проходящих через начало
координат и касающихся прямых
уравнение окружностей, которые, имея центры на
прямой
касаются прямых
окружностей, проходящих через точку А(-1; 5) и
касающихся прямых
окружностей, касающихся прямых
окружностей, касающихся прямых
нижеприводимых уравнений определяют окружности?
Найти центр С и радиус R каждой из них: 397.1
линии определяются следующими уравнениями.
Изобразить эти линии на чертеже. 398.1
расположена точка А(1; -2) относительно каждой из
следующих окружностей – внутри, вне или на
контуре: 399.1
уравнение линии центров двух окружностей,
заданных уравнениями: 400.1
уравнение диаметра окружности
к прямой
кратчайшее расстояние от точки до окружности в
каждом из следующих случаев: 402.1 А(6; -8),
координаты точек пересечения прямой
окружности
расположена прямая относительно окружности
(пересекает ли, касаетлся или проходит вне ее),
если прямая и окружность заданы следующими
уравнениями: 404.1
каких значениях углового коэффициента k прямая
окружность
окружности; 405.3 проходит вне этой
окружности. 406 Вывести условие,
при котором прямая
диаметра окружности
через середину хорды, отсекаемой на прямой
уравнение хорды окружности
в точке М(8,5; 3,5) пополам. 409 Определить длину
хорды окружности
А(1; 2) пополам. 410 Дано уравнение
пучка прямых
на которых окружность
длиною
в точках М1(x1, y1), М2(x2, y2). Доказать, что любая окружность,
проходящая через точки М1, М2, а также
прямая М1М2 могут быть определены уравнением
вида
уравнение окружности, проходящей через точку А(1;
-1) и точки пересечения окружностей
уравнение окружности, проходящей через начало
координат и точки пересечения окружностей
уравнение прямой, проходящей через точки
пересечения окружностей
расстояние от центра окружности
прямой, проходящей через точки пересечения
окружностей
общей хорды окружностей
лежит на прямой
уравнение этой окружности, если известно, что она
проходит через точки пересечения окружностей
уравнение касательной к окружности
точке А(-1; 2). 419 Составить
уравнение касательной к окружности
точке А(-5; 7). 420 На окружности
вычислить расстояние d от точки М1 до этой прямой. 421 Точка М1(x1,
y1) лежит на окружности
уравнение касательной к этой окружности в точке
М1. 422 Точка М1(x1,
y1) лежит на окружности
уравнение касательной к этой окружности в точке
М1. 423 Определить острый
угол, образованный при пересечении прямой
и окружности называется угол между прямой и
касательной к окружности, проведенной к точке их
пересечения). 424 Определить, при
каким углом пересекаются окружности
окружностями называется угол между их
касательными в точке пересечения). 425 Вывести условие,
при котором окружности
прямым углом. 426 Доказать, что
окружности
проведены касательной к окружности
их уравнения. 428 Из точки А(1; 6)
проведены касательные к окружности
их уравнения. 429 Дано уравнение
пучка прямых
которые касаются окружности
проведены касательные к окружности
угол, образованный этими касательными. 431 Из точки Р(2; -3)
проведены касательные к окружности
уравнение хорды, соединяющий точки касания. 432 Из точки С(6; -8)
проведены касательные к окружности
расстояние d от точки С до хорды, соединяющей
точки касания. 433 Из точки Р(-9; 3)
проведены касательные к окружности
расстояние d от центра окружности до хорды,
соединяющей точки касания. 434 Из точки Р(4; -4)
проведены касательные к окружности
длину d хорды, соединяющей точки касания. 435 Вычислить длину
касательной, проведенной из точки А(1; -2) к
окружности
уравнение касательных к окружности
прямой
уравнения касательных к окружности
к прямой
уравнение окружности в полярных координатах в
полярных координатах по данному радиусу R и
полярным координатам центра C(R,
уравнение окружности в полярных координатах по
данному радиусу R и полярным координатам центра
окружности: 439.1 C(R, 0); 439.2 C(R,
полярные координаты центра и радиус каждой из
следующих окружностей: 440.1
уравнениями в полярных координатах. Составить их
уравнения в декартовых прямоугольных
координатах при условии, что полярная ось
совпадает с положительной полуосью Ох, а полюс –
с началом координат. 441.1
Окружности
заданы уравнениями в декартовых прямоугольных
координатах. Составить уравнения этих
окружностей в полярных координатах при условии,
что полярная ось совпадает с положительной
полуосью Ох, а полюс – с началом координат.
уравнение касательной к окружности
точке М1(R,
Как найти точку пересечения окружностей
Геометрические задачи, решаемые аналитически при помощи приемов алгебры, являются неотъемлемой частью программы школьного обучения. Кроме логического и пространственного мышления они развивают понимание ключевых взаимосвязей между сущностями окружающего мира и абстракциями, применяемыми людьми для формализации отношений между ними. Нахождение точек пересечения простейших геометрических фигур — один из типов подобных задач.
Инструкция
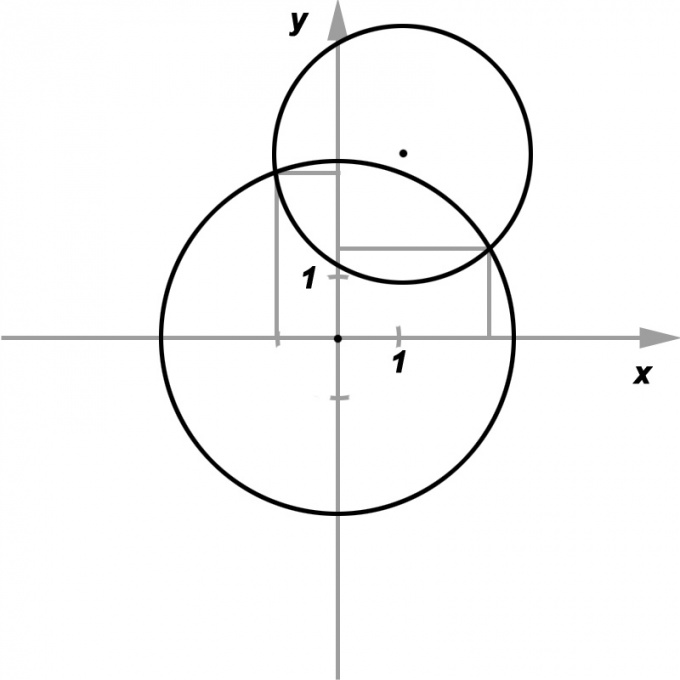
Предположим, что даны две окружности, заданные своими радиусами R и r, а также координатами их центров — соответственно (x1, y1) и (x2, y2). Требуется вычислить, пересекаются ли эти окружности, и если да, то найти координаты точек пересечения.Для простоты можно предположить, что центр одной из заданных окружностей совпадает с началом координат. Тогда (x1, y1) = (0, 0), а (x2, y2) = (a, b). Также имеет смысл предполагать, что a ≠ 0 и b ≠ 0.
Таким образом, координаты точки (или точек) пересечения окружностей, если они есть, должны удовлетворять системе из двух уравнений:x^2 + y^2 = R^2,
(x — a)^2 + (y — b)^2 = r^2.
После раскрытия скобок уравнения приобретают вид:x^2 + y^2 = R^2,
x^2 + y^2 — 2ax — 2by + a^2 + b^2 = r^2.
Теперь первое уравнение можно вычесть из второго. Таким образом, квадраты переменных исчезают, и возникает линейное уравнение: -2ax — 2by = r^2 — R^2 — a^2 — b^2. С его помощью можно выразить y через x:y = (r^2 — R^2 — a^2 — b^2 — 2ax)/2b.
Если подставить найденное выражение для y в уравнение окружности, задача сводится к решению квадратного уравнения: x^2 + px + q = 0, гдеp = -2a/2b,
q = (r^2 — R^2 — a^2 — b^2)/2b — R^2.
Корни этого уравнения позволят найти координаты точек пересечения окружностей. Если уравнение неразрешимо в действительных числах, то окружности не пересекаются. Если корни совпадают между собой, то окружности касаются друг друга. Если корни различны, то окружности пересекаются.
Если a = 0 или b = 0, то исходные уравнения упрощаются. Например, при b = 0 система уравнений примет вид:x^2 + y2 = R^2,
(x — a)^2 + y^2 = r^2.
После вычитания первого уравнения из второго получается:- 2ax + a^2 = r^2 — R^2.Его решение: x = — (r^2 — R^2 — a2)/2a. Очевидно, что в случае b = 0 центры обеих окружностей лежат на оси абсцисс, и у точек их пересечения будет одинаковая абсцисса.
Это выражение для x можно подставить в первое уравнение окружности и получить квадратное уравнение относительно y. Его корни — ординаты точек пересечения, если таковые существуют. Аналогичным образом находится выражение для y, если a = 0.
Если a = 0 и b = 0, но при этом R ≠ r, то одна из окружностей заведомо находится внутри другой, и точки пересечения отсутствуют. Если же R = r, то окружности совпадают, и точек их пересечения бесконечно много.
Если ни у одной из двух окружностей центр не совпадает с началом координат, то их уравнения будут иметь вид:(x — x1)^2 + (y — y1)^2 = R^2,
(x — x2)^2 + (y — y2)^2 = r^2.Если перейти к новым координатам, получающимся из старых методом параллельного переноса: x′ = x + x1, y′ = y + y1, то эти уравнения приобретают вид:x′^2 + y′^2 = R^2,
(x′ — (x1 + x2))^2 + (y′ — (y1 + y2))^2 = r^2.Задача, таким образом, сводится к предыдущей. Найдя решения для x′ и y′, можно легко вернуться к изначальным координатам, обратив уравнения для параллельного переноса.
Источники:
- как найти точки пересечения окружности с прямой
|
90 / 58 / 7 Регистрация: 07.02.2010 Сообщений: 728 |
|
|
1 |
|
Точка пересечения двух окружностей01.04.2011, 12:37. Показов 21297. Ответов 25
Здрям! Даны две окружности радиусами R1 и Rp. Они пересекаются в двух точках. Если подставить числовые данные, то вычисляется точка пересечения c координатами (61,91;99,66), но если решать аналитически без подстановки значений (а мне именно так и надо), то ничего не получается. P.S. «Выражаешь первое через второе, а дальше сам догадаешься» — а вот нет, не догадываюсь. Ничего дальше-то и не считается и не сходится у меня
0 |
|
4652 / 3404 / 361 Регистрация: 11.11.2010 Сообщений: 6,205 Записей в блоге: 2 |
|
|
01.04.2011, 13:05 |
2 |
|
2 уравнение раскрыть, и получится что-то x^2+…+y^2, где x^2+y^2=3600
0 |
|
1 / 1 / 0 Регистрация: 12.01.2011 Сообщений: 7 |
|
|
01.04.2011, 13:07 |
3 |
|
X^2 + Y^2 = R1^2 раскрываем скобки во втором уравнении, получим: выделенная часть свернется в R1^2 уравнение придет к такому виду: C1*x+C2*y=C3 где С1 С2 и С3 — коэффициенты, выражаемые через начальные условия Кстати попробуйте найти их сами дальее из полученного выражения выразим например Y (но можно и Х) Y= C3/C2 — C1*X/C2 И подставим в первое уравнение. далее просто находим Y из полученного квадратного уравнения А как найти Х при известном Y, мне кажется, вам понятно
0 |
|
90 / 58 / 7 Регистрация: 07.02.2010 Сообщений: 728 |
|
|
01.04.2011, 17:17 [ТС] |
4 |
|
Z.I.V, Camelius, спасибо за ответы, но будьте добры без «стандартная схема» и «попробуйте найти сами».
0 |
|
1 / 1 / 0 Регистрация: 12.01.2011 Сообщений: 7 |
|
|
01.04.2011, 21:28 |
5 |
|
X^2 -2*X*Xp + Xp^2 + Y^2 — 2*Y*Yp + Yp^2 = Rp^2 R1^2 -2*X*Xp + Xp^2 — 2*Y*Yp + Yp^2 = Rp^2 2*X*Xp=R1^2 + Xp^2 — 2*Y*Yp + Yp^2 — Rp^2 В строке ниже X выражен через Y R1^2 + Xp^2 + Yp^2 — Rp^2 )/(2*Xp) — (Yp/Xp )*Y вместо X Проще расписать невозможно. Получившееся квадратное уравнение все таки решите сами -не бином ньютона. единственно — писать много, тк не числа а общий вид PS мы не решаем ваше домашнеесеместровое за вас, а помогаем с решением в сложных моментах Добавлено через 11 минут
Если подставить числовые данные, то вычисляется точка пересечения c координатами (61,91;99,66), но если решать аналитически без подстановки значений (а мне именно так и надо), то ничего не получается. И кстати у вас получается не одна точка с 4 координатами а две с двумя
1 |
|
90 / 58 / 7 Регистрация: 07.02.2010 Сообщений: 728 |
|
|
02.04.2011, 04:12 [ТС] |
6 |
|
PS мы не решаем ваше домашнеесеместровое за вас, а помогаем с решением в сложных моментах Это не домашнее задание, это б****, кусок научного труда, с которым я бьюсь уже третью неделю
И кстати у вас получается не одна точка с 4 координатами а две с двумя Да, я знаю, что квадратное уравнение имеет два корня, но построение дуги производится в первой четверти, так что точку принимать буду одну. Спасибо за помощь!
0 |
|
90 / 58 / 7 Регистрация: 07.02.2010 Сообщений: 728 |
|
|
05.04.2011, 10:22 [ТС] |
7 |
|
Не смог я таки решить. Прилагаю свое решение, подскажите, где ошибка.
0 |
|
1 / 1 / 0 Регистрация: 12.01.2011 Сообщений: 7 |
|
|
10.04.2011, 18:22 |
8 |
|
Сведите эту систему к более простой перенесите центр координат в центр одной из окружностей то бишь сделайте замену U=х-хс V=y-yc Это резко упростит вид уравнения и сведет к тому что было показано выше а после получения результата просто перейдите к исходной сетке координат
0 |
|
90 / 58 / 7 Регистрация: 07.02.2010 Сообщений: 728 |
|
|
11.04.2011, 17:38 [ТС] |
9 |
|
Вот именно таким образом я еще и не решал за последний месяц. Спасибо!!!
0 |
|
4865 / 3287 / 468 Регистрация: 10.12.2008 Сообщений: 10,570 |
|
|
12.04.2011, 10:18 |
10 |
|
Дано: Rp = 90 Даны две окружности радиусами R1 и Rp. Они пересекаются в двух точках. там много окружностей с радиусами R1
0 |
|
90 / 58 / 7 Регистрация: 07.02.2010 Сообщений: 728 |
|
|
12.04.2011, 17:42 [ТС] |
11 |
|
accept, там две окружности: ротора и статор. Мне символьное решение поиска точек пересечения надо. Не получается оно.
0 |
|
4865 / 3287 / 468 Регистрация: 10.12.2008 Сообщений: 10,570 |
|
|
13.04.2011, 02:29 |
12 |
|
Код общее (x - x0) ^ 2 + (y - y0) ^ 2 = R ^ 2 частные (x - x1) ^ 2 + (y - y1) ^ 2 = R1 ^ 2 (x - x2) ^ 2 + (y - y2) ^ 2 = R2 ^ 2 частные со значениями (x - x1) ^ 2 + (y - y1) ^ 2 = 90 ^ 2 (x - x2) ^ 2 + (y - y2) ^ 2 = 80 ^ 2 частные со всеми первоначальными значениями (x - x1) ^ 2 + (y - y1) ^ 2 = 60 ^ 2 (x - 63) ^ 2 + (y - 9,67) ^ 2 = 90 ^ 2 какие две точки пересечения ты пытаешься найти, если их там огромное множество, (притом, по обновлённым данным центр второй окружности тоже может быть любым, как и первой, какие две точки ? )
0 |
|
90 / 58 / 7 Регистрация: 07.02.2010 Сообщений: 728 |
|
|
13.04.2011, 06:33 [ТС] |
13 |
|
Радиусы окружностей известны, координаты центров зависят друг от друга. У меня есть входные координаты.
0 |
|
4865 / 3287 / 468 Регистрация: 10.12.2008 Сообщений: 10,570 |
|
|
13.04.2011, 07:15 |
14 |
|
координаты центров зависят друг от друга. какие там радиусы и центры ?
У меня есть входные координаты. координаты центров ?
0 |
|
5 / 3 / 2 Регистрация: 09.06.2010 Сообщений: 89 |
|
|
13.04.2011, 14:01 |
15 |
|
дайте конкретнее значения
0 |
|
90 / 58 / 7 Регистрация: 07.02.2010 Сообщений: 728 |
|
|
21.04.2011, 07:01 [ТС] |
16 |
|
для статора: Для ротора:
0 |
|
4865 / 3287 / 468 Регистрация: 10.12.2008 Сообщений: 10,570 |
|
|
26.04.2011, 08:50 |
17 |
|
0 |
|
90 / 58 / 7 Регистрация: 07.02.2010 Сообщений: 728 |
|
|
26.04.2011, 11:23 [ТС] |
18 |
|
accept, у меня есть и математическое и геометрчиеское решения (с точностью до 25 знаков после запятой). у1,2 = хс*Рс/ус + ус*РС
0 |
|
57 / 57 / 1 Регистрация: 19.04.2011 Сообщений: 136 |
|
|
26.04.2011, 15:42 |
19 |
|
В новом базисе, где xc=yc=0, sqrt — корень квадратный, значение которого и будет определять количество решений.
0 |
|
4865 / 3287 / 468 Регистрация: 10.12.2008 Сообщений: 10,570 |
|
|
27.04.2011, 04:11 |
20 |
|
у меня есть и математическое и геометрчиеское решения надо вычислить расстояние межу центрами и сравнить его с суммой радиусов
Мне надо символьное решение, т.е, к примеру
А цифры для проверки символьного решения. нет, вот как раз эти цифры задают две определённые окружности, которые при пересечении дают две определённые точки после доказательства, что они пересекаются, найди эти две точки, решив систему
0 |
|
IT_Exp Эксперт 87844 / 49110 / 22898 Регистрация: 17.06.2006 Сообщений: 92,604 |
27.04.2011, 04:11 |
|
Помогаю со студенческими работами здесь
Найти геометрическое место центров окружностей, касающихся двух данных окружностей
Искать еще темы с ответами Или воспользуйтесь поиском по форуму: 20 |








 Даны координаты двух вершин треугольника и точка пересечения его высот
Даны координаты двух вершин треугольника и точка пересечения его высот