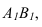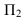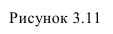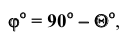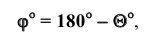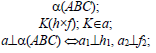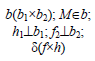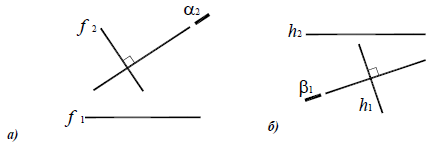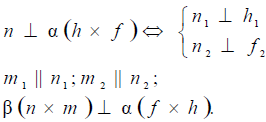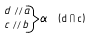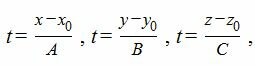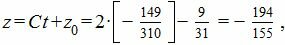Расстояние от точки до плоскости онлайн
С помощю этого онлайн калькулятора можно найти расстояние от точки до заданной плоскости. Дается подробное решение с пояснениями. Для вычисления расстояния от точки до плоскости введите координаты точки и коэффициенты уравнения плоскости в ячейки и нажимайте на кнопку «Решить».
Предупреждение
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Расстояние от точки до плоскости − теория, примеры и решения
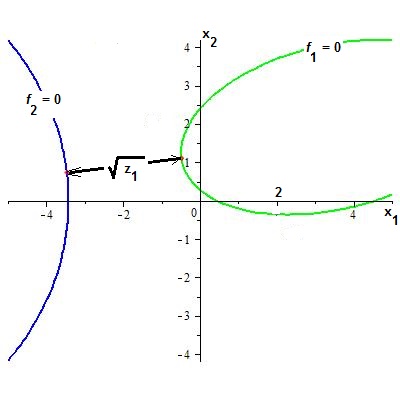
Для нахождения расстояния от точки M0 до плоскости α, необходимо найти расстояние от точки M0 до проекции точки M0 на плоскость α:
Нахождение расстояния от точки до плоскости содержит следующие шаги:
- построение прямой L, проходящей через точку M0 и перпендикулярной плоскости α.
- нахождение точки M1 пересечения плоскости α с прямой L(Рис.1).
- вычисление расстояния между точками M0 и M1.
1. Общее уравнение плоскости имеет вид:
где n(A,B,C)− называется нормальным вектором плоскости.
Уравнение прямой, проходящей через точку M0(x0, y0, z0) и имеющий направляющий вектор q(l, m, n) имеет следующий вид:
Для того, чтобы прямая (2) была ортогональна плоскости (1), направляющий вектор q(l, m, n) прямой (2) должен быть коллинеарным нормальному вектору n(A,B,C) плоскости (1)(Рис. 1). Следовательно, в качестве направляющего вектора прямой (2) можно взять нормальный вектор плоскости (1) .
Таким образом, уравнение прямой, проходящей через точку M0(x0, y0, z0) и ортогональной плоскости (1) имеет следующий вид:
Для нахождения точку пересечения прямой L с плоскостью α, проще всего рассматривать параметрическое уравнение прямой. Составим ее
Выразим переменные x, y, z через рараметр t.
2. Найдем точку пересечения прямой (4) с плоскостью (1). Для этого нужно найти такой параметр t, при котором точка M(x, y, z) принадлежит плоскости (1). Поэтому подставим значения x,y,z из выражения (4) в (1) и решим относительно t.
A(At+x0)+B(Bt+y0)+C(At+z0)+D=0,
A 2 t+Ax0+B 2 t+By0+C 2 t+Cz0+D=0,
3. Найдем, наконец, расстояние от точки M0 до плоскости (1). Очевидно, что расстояние от точки M0 до плоскости (1) − это расстояние от точки M0 до точки M1. А это расстояние вычисляется так:
Учитывая значение параметра t, имеем:
Пример 1. Найти расстояние от точки M0(2, -1, -9/31) до плоскости
Нормальный вектор плоскости имеет вид:
Подставляя координаты точки M0 и нормального вектора плоскости в (5), получим:
Из выражений (4) находим:
Проекцией точки M0(2, -1, -9/31) на плоскость (7) является точка:
Вычислим расстояние между точками M0 и M1:
Расстояние от точки M0(2, -1, -9/31) до плоскости (7):
Онлайн калькулятор. Расстояние от точки до плоскости
Предлагаю вам воспользоваться онлайн калькулятором для вычисления расстояния от точки до плоскости.
Воспользовавшись онлайн калькулятором, вы получите детальное пошаговое решение вашей задачи, которое позволит понять алгоритм решения задач на вычисление расстояния от точки до плоскости и закрепить пройденный материал.
Найти расстояние от точки до плоскости
Ввод данных в калькулятор для вычисления расстояния от точки до плоскости
В онлайн калькулятор вводить можно числа или дроби. Более подробно читайте в правилах ввода чисел.
Дополнительные возможности калькулятора для вычисления расстояния от точки до плоскости
- Используйте кнопки и на клавиатуре, для перемещения между полями калькулятора.
Теория: Расстояние от точки до плоскости
Расстояние от точки до плоскости — равно длине перпендикуляра, опущенного из точки на плоскость.
Если задано уравнение плоскости A x + B y + C z + D = 0, то расстояние от точки M(M x , M y , M z ) до плоскости можно найти используя следующую формулу
| d = | |A·M x + B·M y + C·M z + D| |
| √ A 2 + B 2 + C 2 |
Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел.
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Решение задач по математике онлайн
//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘
Калькулятор онлайн.
Вычисление расстояния от точки до плоскости
Этот калькулятор онлайн вычисляет расстояния от точки до плоскости заданной в виде общего уравнения плоскости:
$$ Ax+By+Cz+D=0 $$
Онлайн калькулятор для вычисления расстояния от точки до плоскости не просто даёт ответ задачи, он приводит подробное решение с пояснениями, т.е. отображает процесс решения для того чтобы проконтролировать знания по математике и/или алгебре.
Этот калькулятор онлайн может быть полезен учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.
Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.
Наш онлайн калькулятор дает не только ответ задачи, но и отображает процесс решения по шагам. В результате вы сможете понять процесс решения задач на нахождение расстояния от точки до плоскости.
Если вы не знакомы с правилами ввода чисел, рекомендуем с ними ознакомиться.
Числа можно вводить целые или дробные.
Причём, дробные числа можно вводить не только в виде десятичной, но и в виде обыкновенной дроби.
Правила ввода десятичных дробей.
В десятичных дробях дробная часть от целой может отделяться как точкой так и запятой.
Например, можно вводить десятичные дроби так: 2.5 или так 1,3
Правила ввода обыкновенных дробей.
В качестве числителя, знаменателя и целой части дроби может выступать только целое число.
Знаменатель не может быть отрицательным.
При вводе числовой дроби числитель отделяется от знаменателя знаком деления: /
Ввод: -2/3
Результат: ( -frac<2> <3>)
Целая часть отделяется от дроби знаком амперсанд: &
Ввод: -1&5/7
Результат: ( -1frac<5> <7>)
http://ru.onlinemschool.com/math/assistance/cartesian_coordinate/p_plane/
http://www.math-solution.ru/math-task/lp-dist-point-plain
Расстояние
от точки до плоскости можно определить
одним из следующих способов:
1)
прямым путем: опустить перпендикуляр
из точки на плоскость, найти основание
перпендикуляра и определить расстояние
между точками – заданной и найденной;
2)
вращением привести заданную систему в
положение, когда плоскость перпендикулярна
какой-либо плоскости проекций;
3)
совмещением: провести через точку
горизонтально или вертикальнопроецирующую
плоскость, перпендикулярную к заданной
плоскости, и совмещением вспомогательной
плоскости с какой-либо плоскостью
проекций найти положение заданной точки
и линии пересечения плоскостей;
4)
заменой плоскостей проекций: заменить
одну из плоскостей проекций новой,
которая перпендикулярна заданной
плоскости.
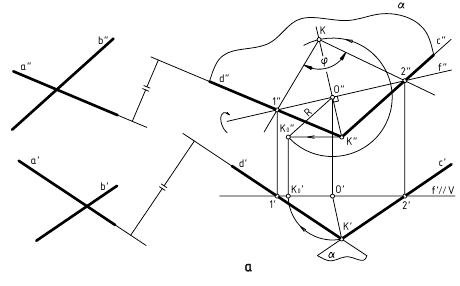
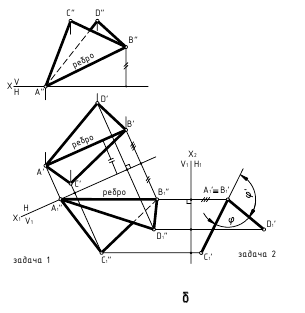
Задача
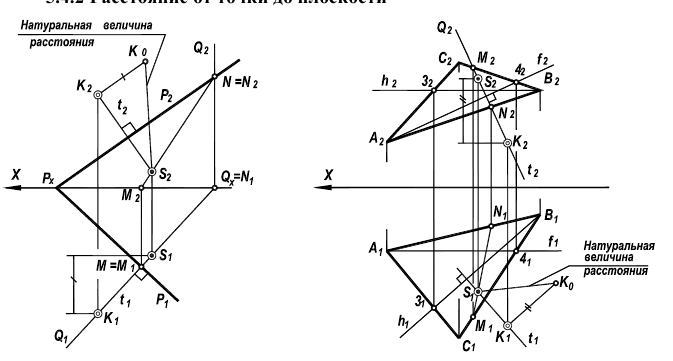
11. Определить
расстояние от точки К до плоскости
треугольника ABC (рис. 14) методом замены
плоскостей проекций.
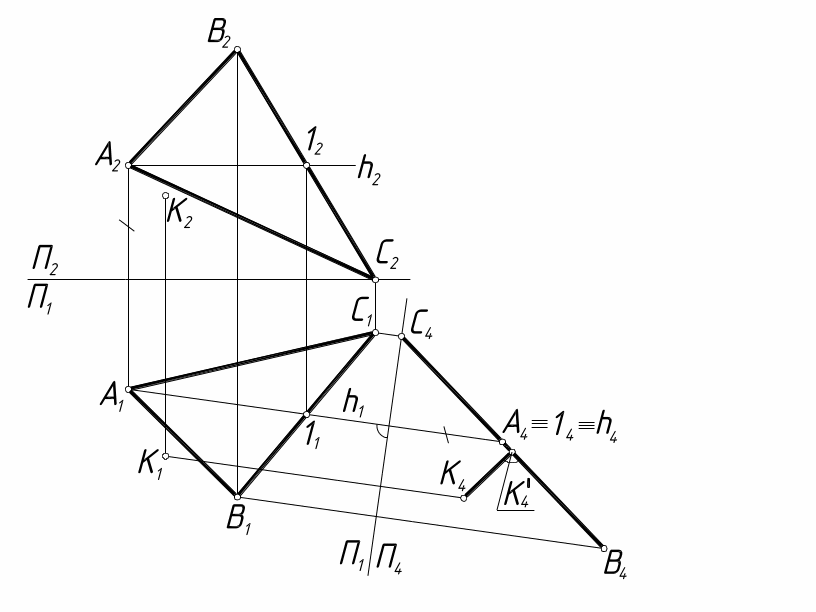
Рис.
14. Определение расстояния от точки до
плоскости
Решение.
Заменяем плоскость проекций П2
П4.
Проводим горизонталь в плоскости
треугольника. Новая ось проекций X1
h1.
Находим проекции
точки К4
и треугольника А4В4С4.
Опускаем из точки К4
перпендикуляр на проекцию треугольника
А4В4С4.
Отрезок К4
К4‘
является искомым расстоянием.
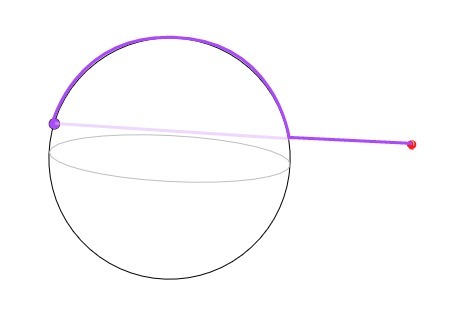
2.4. Определение расстояния от точки до поверхности вращения
Расстояние
от точки до
поверхности вращения
измеряется величиной отрезка нормали,
проведенной из заданной точки. Основание
нормали лежит на ближайшей точке
меридиана, расположенного в одной
плоскости с заданной точкой и осью
вращения.
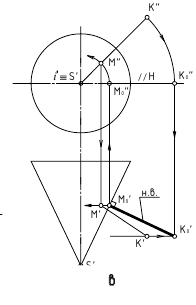
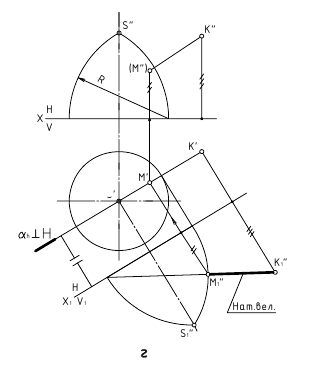
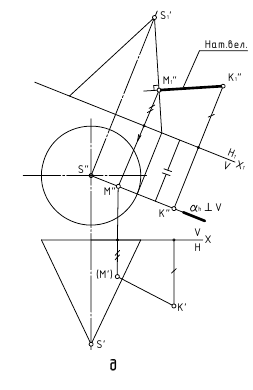
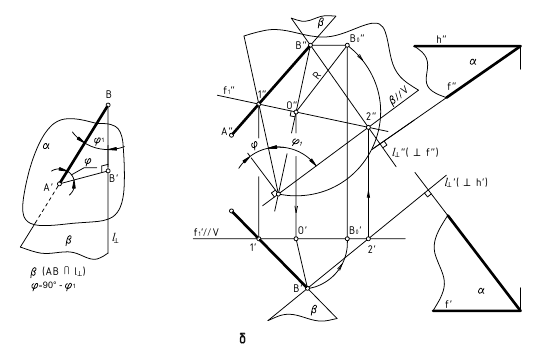
Задача
12. Найти
расстояние от точки до
поверхности вращения
(рис.
15).

а
б в
Рис.
15. Определение расстояния от точки до
сферы
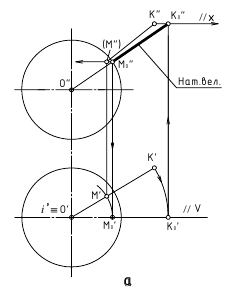
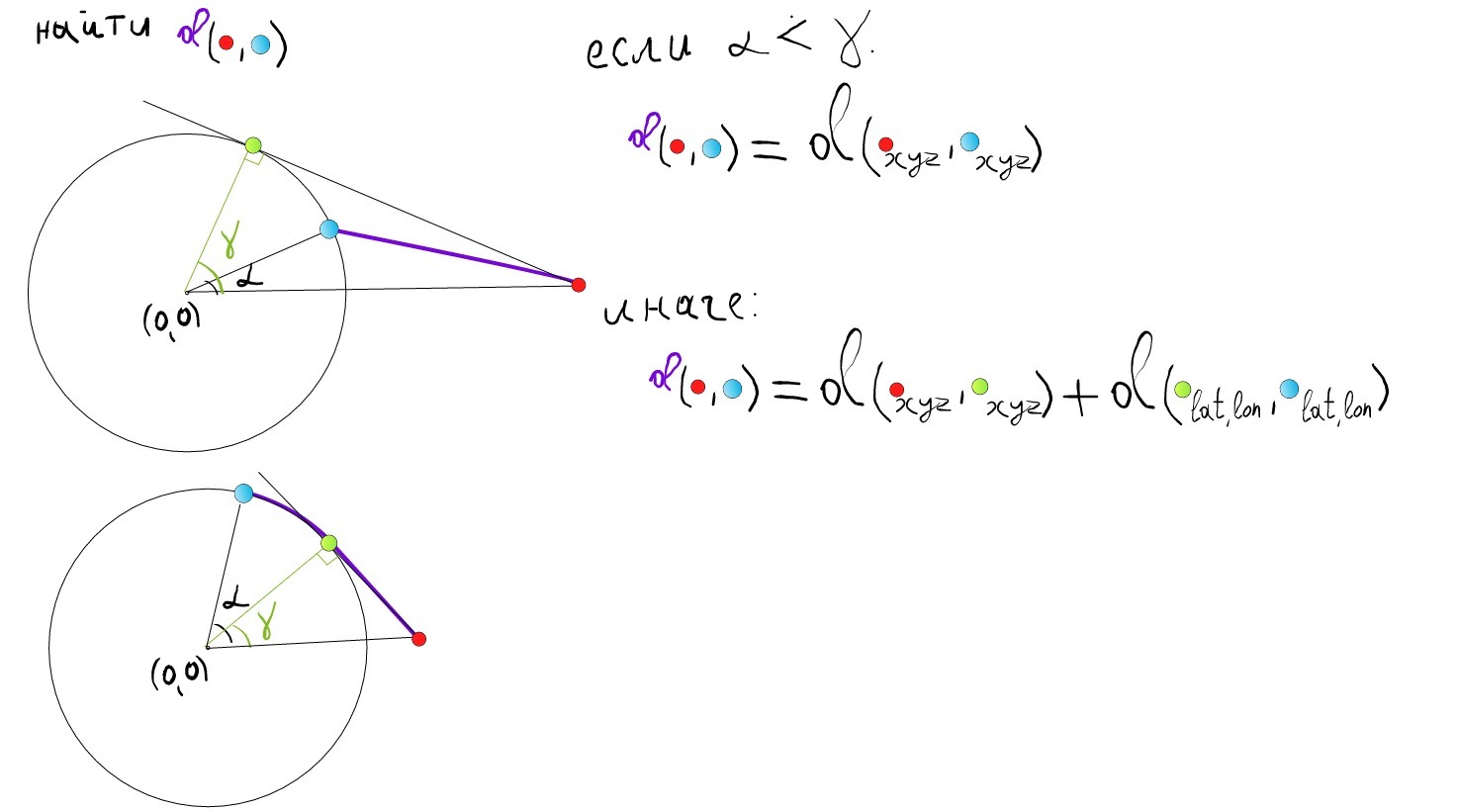
Решение.
Если бы точка А находилась в одной
плоскости с меридианом или экватором,
тогда достаточно было бы соединить
соответствующую проекцию с центром,
чтобы определить искомое.
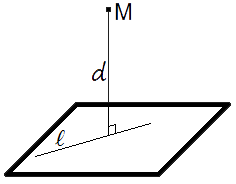
Решим
эту задачу вращением вокруг фронтально
проецирующей пря-
мой – оси i, проходящей
через центр сферы. Введем плоскость-посредник
– фронтально Σ2
проецирующую плоскость через заданную
точку А2
и ось i2.
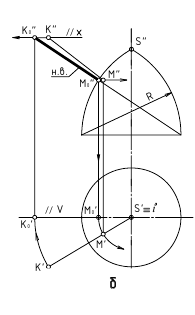
Плоскость Σ пересекает сферу по
полуокружности, которая на плоскость
П1
проецируется в полуэллипс. Повернем
плоскость Σ2
вместе с точкой А2
вокруг оси до горизонта. Теперь сечение
плоскостью Σ’2
спроецируется на П1
без искажения и совпадет с проекцией
экватора, значит, новая проекция точки
А’2
лежит в одной плоскости с экватором.
Соединим А’1
с О1
и там, где этот отрезок пересечет экватор,
обозначим точку М1.
Отрезок
А’1М’1
измеряет расстояние от точки А’ до
преобразованного
сечения сферы.
Этот отрезок определяет расстояние от
точки А до сферы, а точка М – ближайшая
точка сферы к точке А.
2.5. Определение расстояния между параллельными прямыми
Расстояние
между параллельными прямыми
измеряется
отрезком перпендикуляра между ними.
Задача
13. Найти
расстояние между параллельными прямыми
общего положения методом замены
плоскостей проекций.
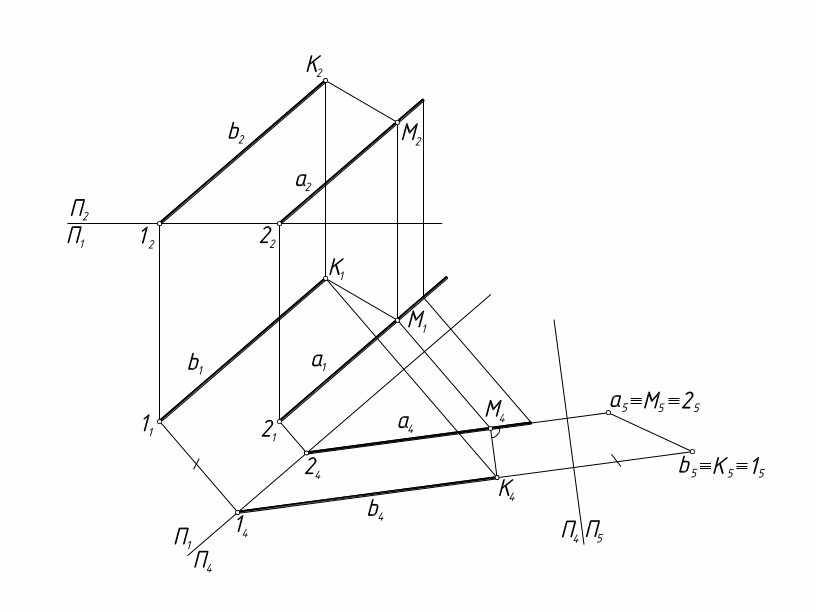
Рис.
16. Определение расстояния между
параллельными прямыми
Решение.
Сначала построено изображение прямых
на плоскости П1
П4.
В этой системе плоскостей прямые занимают
положение линии уровня:
а1(b1)||
П4
(рис. 16).
В
системе плоскостей П4
П5
прямые занимают проецирующее по отношению
к плоскости П5
положение: П5
а4(b4).
Отрезок M5K5
между проекциями прямых определяет
истинную величину расстояния между
прямыми а и b.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание:
К метрическим задачам относятся задачи на определение натуральной величины отрезков, расстояний углов, площадей плоских фигур.
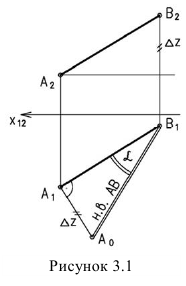
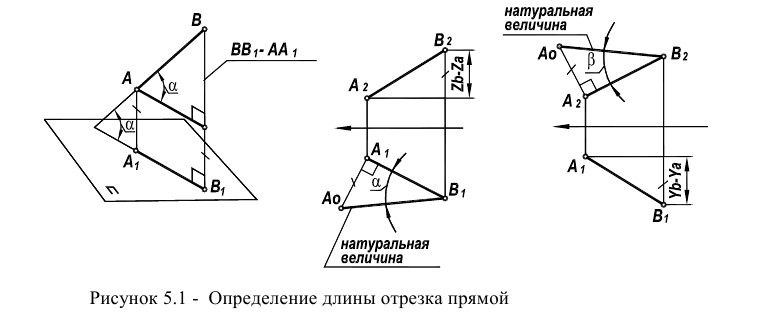
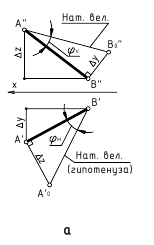
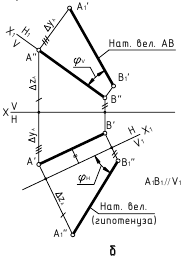
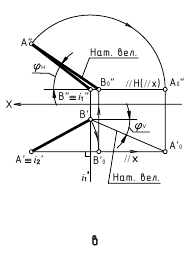
Определение натуральной величины отрезка и углов наклона к плоскостям проекций методом прямоугольною треугольника Натуральная величина отрезка равна гипотенузе прямоугольного треугольника, одним катетом которого является проекция отрезка, а вторым — разность расстояний концов отрезка от той плоскости, на которой ведется построение. При этом угол между гипотенузой и катетом проекций является углом наклона отрезка к той плоскости, ряльной величины выполнено на горизонтальной проекции. Поэтому одним катетом прямоугольного треугольника, является горизонтальная проекция
Если необходимо определить угол наклона отрезка АВ к плоскости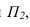
Решение метрических задач методами преобразовании проекций
Положении геометрических образов, при которых расстоянии и углы не искажаются на плоскостях проекций
Метрические характеристики объектов на чертежах не искажаются, если геометрические образы занимают частное положение относительно плоскостей проекций.
Приведем некоторые из них.
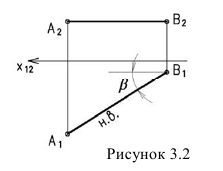
1. Прямая проецируется в натуральную величину, если она параллельна плоскости проекций (рисунок 3.2).
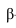
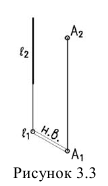
2. Расстояние от точки до прямой проецируется в натуральную величину, если прямая проецирующая (рисунок 3.3).
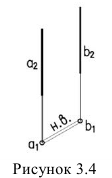
3. Расстояние между параллельными прямыми проецируется в натуральную величину, если прямые проецирующие (рисунок 3.4).
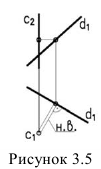
4. Расстояние между скрещивающимися прямыми проецируется в натуральную величину, если одна из прямых проецирующая (рисунок 3.5).
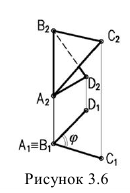
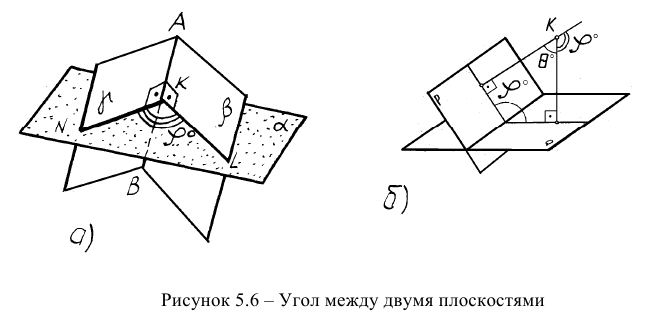
5. Угол между плоскостями (двугранный угол) проецируется в натуральную величину, если ребро угла проецирующее (рисунок 3.6).
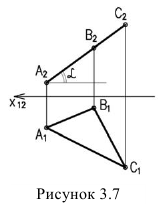
6. Угол наклона плоскости к плоскости проекций проецируется в натуральную величину, если плоскость проецирующая (рисунок 3.7)
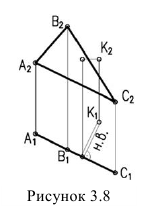
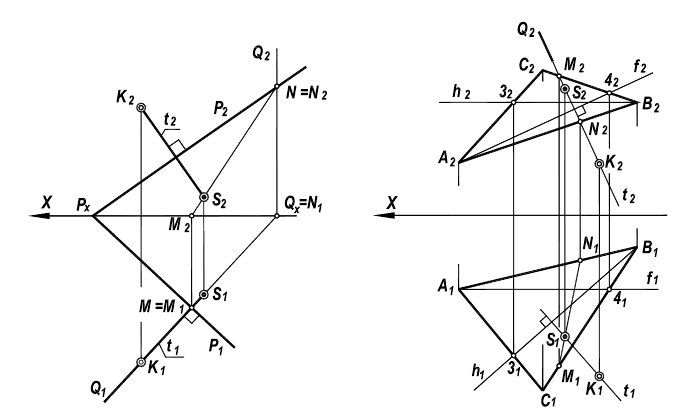
7. Расстояние от точки до плоскости проецируется в натуральную величину, если плоскость проецирующая (рисунок 3.8)
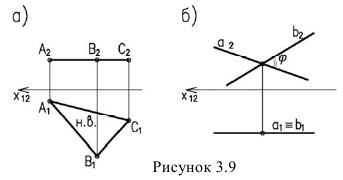
8. Любая плоская фигура проецируется в натуральную величину, если она параллельна плоскости проекций (рисунок 3.9а,б)
Таким образом, для решения метрических задач целесообразно данный объект привести в частное положение с тем, чтобы на одной из новых проекций получить более простое решение задачи.
Для такого перехода и служат способы преобразования проекций.
Существует несколько способов преобразовании проекций: способ вращения вокруг осей перпендикулярных плоскостям проекций, способ плоскопараллельного перемещения, способ замены плоскостей проекций и др.
Четыре основных задачи преобразовании проекций
Этими способами решаются четыре основные задачи:
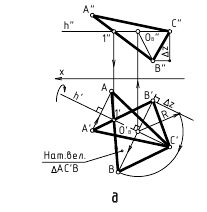
- Задача 1. Прямую общего положения преобразуем в линию уровня (одно преобразование).
- Задача 2. Прямую общего положения преобразуем в проецирующую (два преобразования)
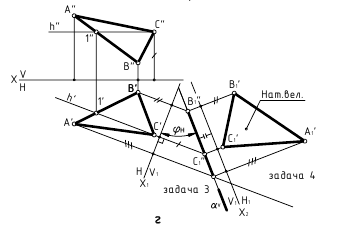
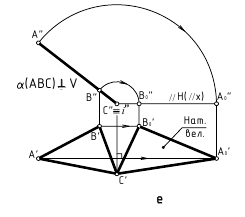
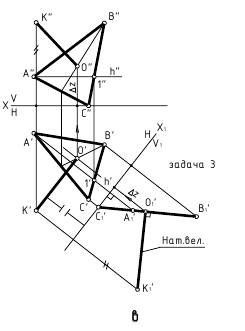
- Задача 3. Плоскость общего положения преобразуем в проецирующую (одно преобразование)
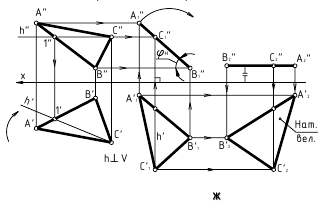
- Задача 4. Плоскость общего положения преобразуем в плоскость уровня (два преобразования)
Решение 1-ой и 2-ой задачи преобразовании проекций методом вращении, плоскопараллельного перемещении и замены плоскостей проекций
Способ вращения
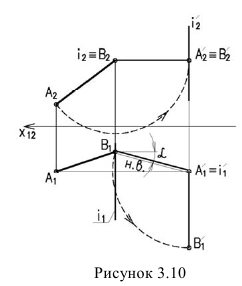
Способ вращения заключается в том, что геометрические образы вращаются вокруг осей перпендикулярных плоскостям проекций до занятия ими какого-либо частного положения относительно плоскостей проекций. При этом одна проекция точки перемещается по окружности, вторая — но прямой параллельной оси проекций.
На рисунке 3.10 вокруг оси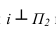
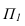
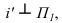
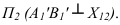
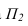
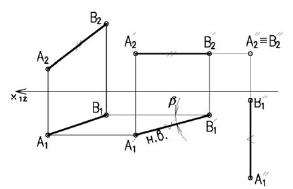
Способ плоскопараллельного перемещения
Способ плоскопараллельного перемещения является разновидностью способа вращения (вращение без закрепленных осей), т.е. положение объекта можно преобразовывать путем перемещения его параллельно одной плоскости проекций, одновременно изменяя его положение относительно другой плоскости проекций до занятия им какого-либо частного положения.
На рисунке 3.11 сначала АВ переводим из общего положения в положение горизонтальное. При этом 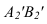
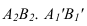
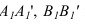
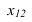
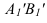
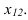
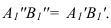
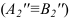
Способ замены плоскостей проекций
Сущность способа замены плоскостей проекций заключается в том, что старая система плоскостей проекций заменяется на новую, с таким расчетом, чтобы относительно новой системы плоскостей, геометрический образ занял какое-то частное положение. При этом нужно помнить, что линии связи будут перпендикулярны относительно новой оси проекций и расстояния от новой оси проекций до новой проекции точки равно расстоянию от старой проекции точки до старой оси.
На рисунке 3.12 произведена первая замена плоскость 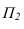
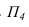
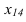
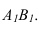
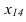
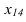
Далее прямую АВ преобразуем в проецирующую. Для этого проводим новую ось 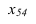
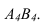
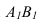
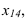
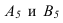
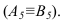
Решение 3-ой и 4-ой задачи преобразовании проекций методом плоскопараллельного перемещения и замены плоскостей проекций
Так как метод вращения является более громоздким, рассмотрим решение 3-ей и 4-ой задачи преобразования методом плоскопараллельного перемещения и методом замены плоскостей проекций.
Способ плоскопараллельного перемещения
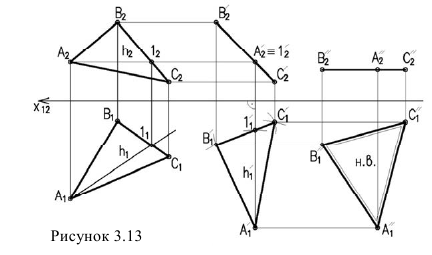
Для того чтобы плоскость из общего положения перевести в проецирующее, нужно иметь ввиду, что при этом ее горизонталь или фронталь должна быть перпендикулярна плоскости проекций. Поэтому на рисунке 3.13 проведена горизонталь 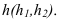
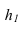
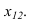
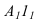
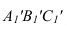
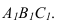
Чтобы плоскость треугольника перевести в положение плоскости уровня, достаточно полученную фронтальную проекцию 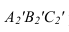
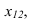
Способ замены плоскостей проекций
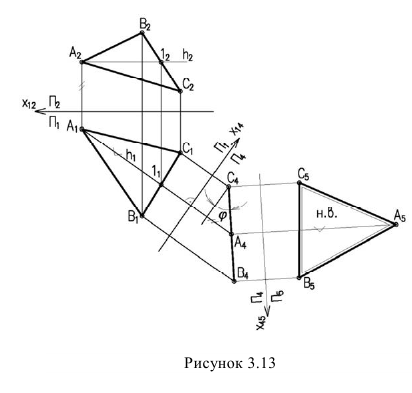
При решении задачи методом замены (рисунок 3.14) новую ось 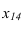
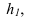
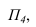
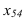
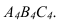
Для того, чтобы методами преобразования решить любую метрическую задачу, необходимо определить какую из четырех основных задач преобразования необходимо решать в каждом конкретном случае.
Метрические задачи
Метрические задачи — это задачи на определение линейных или угловых размеров геометрических объектов, а также расстояний и углов между ними.
Главным вопросом метрических задач является вопрос о построении перпендикуляра к прямой или плоскости. Построение взаимно перпендикулярных прямых было рассмотрено ранее.
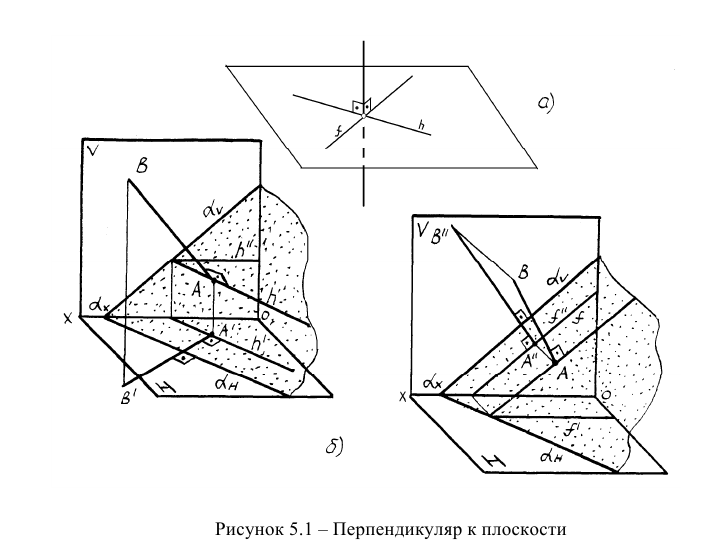
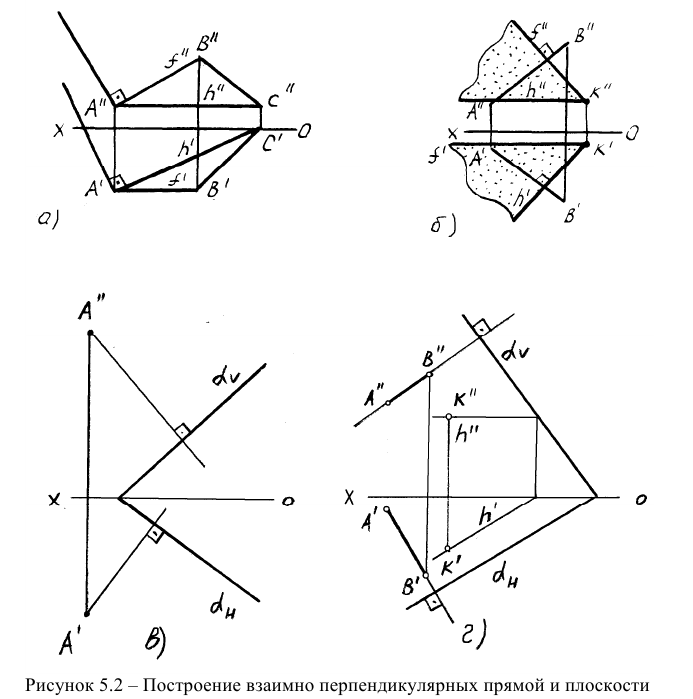
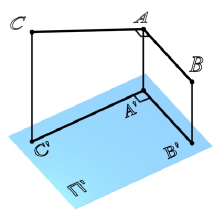
Из элементарной геометрии известно, что прямая перпендикулярна к плоскости, если она перпендикулярна двум пересекающимся прямым, принадлежащим этой плоскости. В качестве этих пересекающихся прямых наиболее целесообразно использовать горизонталь и фронталь плоскости. Это объясняется тем, что только в этом случае прямой угол будет проецироваться в натуральную величину на соответствующие плоскости проекций. На рисунке 5.1 приведен пространственный чертеж, на котором из плоскости а (из точки А) восстановлен перпендикуляр АВ. Из приведенного изображения можно выяснить методику построения проекций перпендикуляра к плоскости: горизонтальная проекция перпендикуляра к плоскости проводится перпендикулярно горизонтальной проекции горизонтали или горизонтальному следу плоскости, а фронтальная проекция перпендикуляра проводится перпендикулярно фронтальной проекции фронтали или фронтальному следу плоскости. Таким образом, необходимо выполнить следующий алгоритм проведения проекций перпендикуляра к плоскости:
Построение перпендикуляра к плоскость и восстановление перпендикуляра из плоскости называется прямой задачей, а построение плоскости, перпендикулярной к прямой — обратной задачей. Обе задачи решаются по одному и тому же вышеописанному алгоритму. При этом плоскость, перпендикулярную заданной прямой, можно задать следами или пересекающимися горизонталью и фронталью.
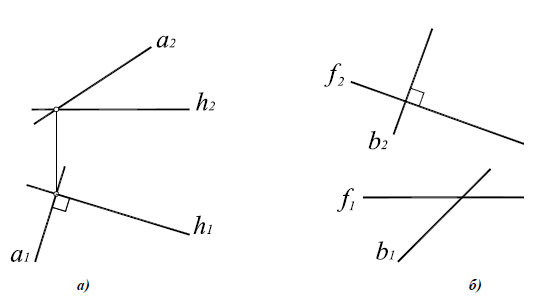
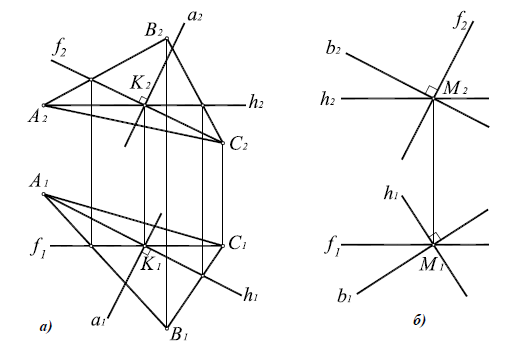
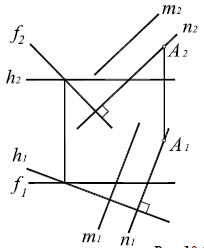
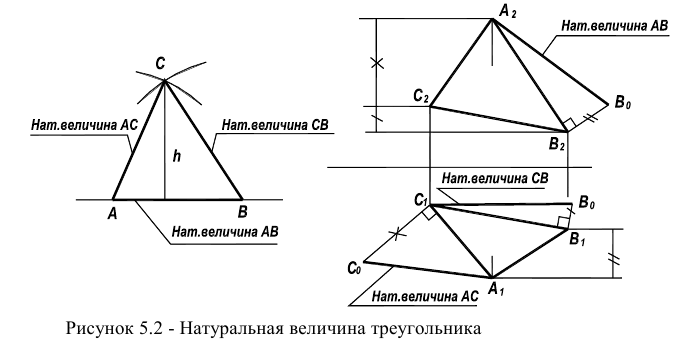
На рисунке 5.2 показано решение прямой (а) и обратной (б) задач. В прямой задаче из точки A треугольника AВС восстановлен перпендикуляр, в обратной задаче через точку К проведена плоскость, перпендикулярная прямой АВ. Плоскость задана пересекающимися горизонталью и фронталью.
Здесь же приведены примеры прямой и обратной задач, если плоскость задана следами. В прямой задаче (в) из точки Л построен перпендикуляр на плоскость, в обратной (г) — через точку К проведена плоскость перпендикулярно прямой АВ.
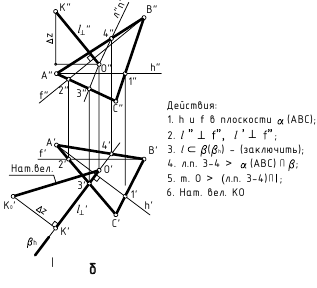
Определение расстояний между геометрическими объектами
Среди этих задач можно выделить следующие задачи: расстояние от точки до плоскости, расстояние от точки до прямой, расстояние между двумя параллельными прямыми, расстояние между двумя скрещивающимися прямыми, расстояние между двумя параллельными плоскостями и другие. В общем случае все задачи сводятся к определению расстояний между двумя точками.
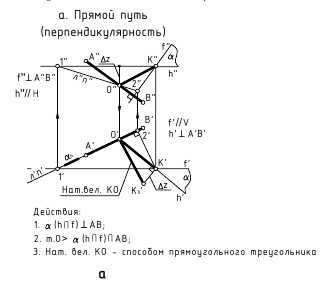
Чтобы определить расстояние от точки до плоскости, необходимо выполнить ряд логических действий:
- Из точки опустить перпендикуляр на заданную плоскость;
- Найти точку встречи перпендикуляра с плоскостью;
- Определить НВ расстояния между заданной и найденной точками.
Задача на определение расстояния от точки до прямой решается по следующему плану:
- Через точку к провести плоскость, перпендикулярную заданной прямой;
- Найти точку встречи М заданной прямой с проведенной плоскостью;
- Соединить полученные точки (это будет перпендикуляр из точки на прямую);
- Определить НВ перпендикуляра.
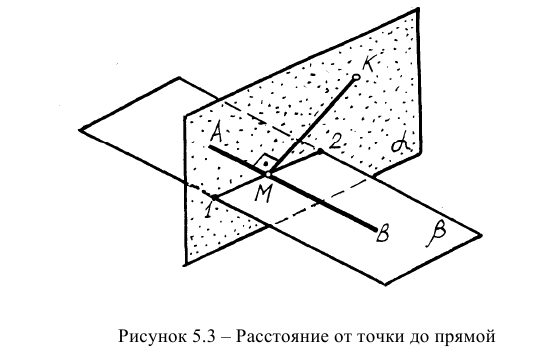
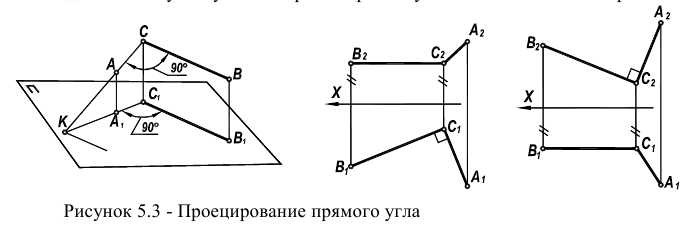
Пространственная модель решения второй задачи представлена на рисунке 5.3. Рассмотренная задача относится также к задачам на перпендикулярность двух прямых.
Другие упомянутые задачи на определение расстояний легче решаются методами преобразования эпюра, которые будут рассмотрены в последующих разделах.
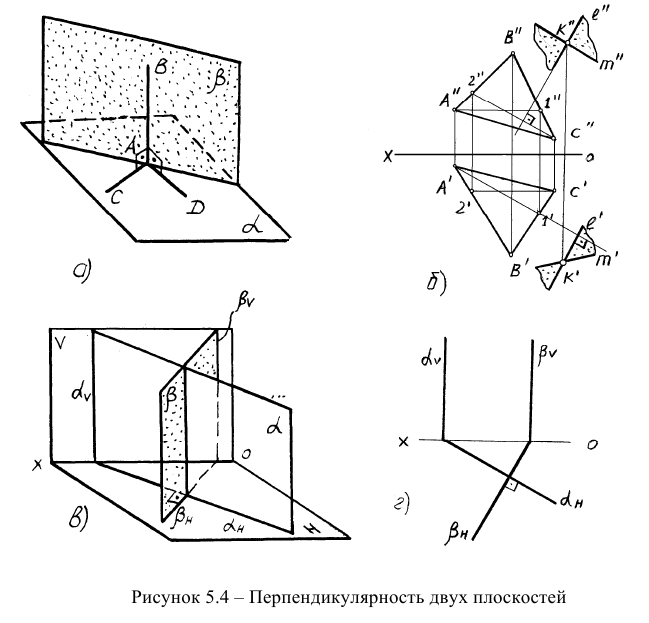
Перпендикулярность плоскостей
Плоскость перпендикулярна другой плоскости, если она содержит прямую, перпендикулярную другой плоскости (рисунок 5.4а). Таким образом, для того, чтобы провести плоскость, перпендикулярную другой, необходимо сначала провести перпендикуляр к заданной плоскости, а затем через него провести искомую плоскость. На рисунке 5.46 представлена задача: через точку К провести плоскость, перпендикулярную плоскости треугольника AВС. Искомая плоскость задана двумя пересекающимися прямыми, одна из которых перпендикулярна заданной плоскости.
Если две плоскости являются одноименными плоскостями частного положения (например, горизонтально- или фронтально-проецирующими), то при перпендикулярности плоскостей их собирательные следы будут перпендикулярны друг другу (рисунок 5.4в,г).
Если плоскости являются плоскостями общего положения, то при их перпендикулярности одноименные следы не будут взаимно перпендикулярны. Другими словами, перпендикулярность одноименных следов плоскостей общего положения не является достаточным условием для перпендикулярности самих плоскостей.
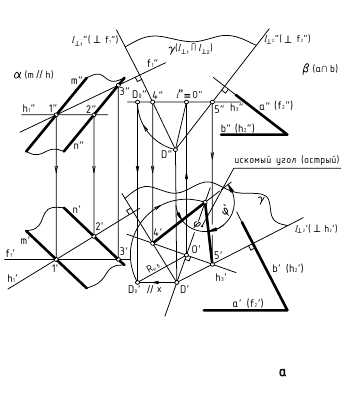
Определение углов между прямой и плоскостью и между двумя плоскостями
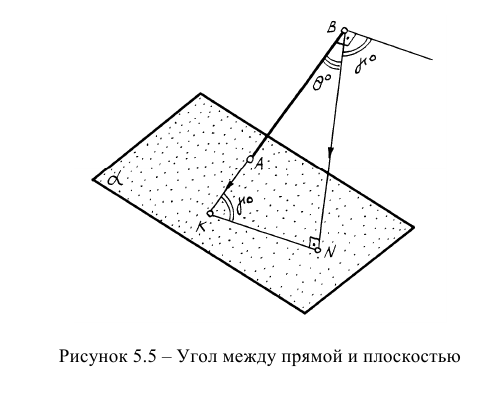
Определение углов между геометрическими объектами является трудоемкой задачей, если её решать традиционными геометрическими способами. Так, например, задачу на определение угла между прямой и плоскостью (рисунок 5.5) можно решить способом, алгоритм которого содержит следующие операции:
- Определить точку встречи прямой АВ с плоскостью а;
- Из точки В построить перпендикуляр на плоскость;
- Найти точку встречи перпендикуляра с плоскостью;
- Точки К и N соединить и определить НВ угла BKN.
Однако задача может быть значительно упрощена, если использовать способ решения задачи с помощью дополнительного угла. Дополнительным углом назовем угол между заданной прямой АВ и перпендикуляром BN, обозначенный через 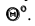
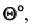
которую можно решить графически, достроив угол 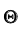
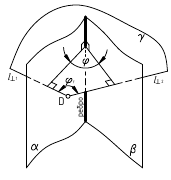
То же самое можно сказать о задаче на определение двугранного угла, то есть угла между двумя плоскостями (рисунок 5.66). Первый способ (геометрический) достаточно трудоемок. Он заключается в пересечении угла вспомогательной плоскостью а, перпендикулярной ребру АВ, построении линий пересечения KN и KL и определении натуральной величины угла NKL.
С помощью дополнительного угла задача решается следующим образом. В растворе двугранного угла (рисунок 5.6в) берут любую точку К и строят из неё перпендикуляры на обе плоскости двугранного угла, которые образуют дополнительный угол 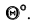
Дополненный угол будет искомым.
Натуральную величину дополнительного угла
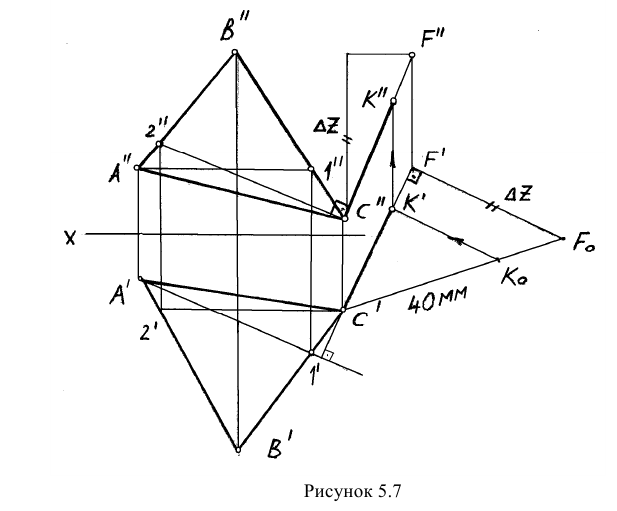
Пример: Из любой вершины треугольника АВС восстановить перпендикуляр длиной 40 мм.
Решение: Сначала необходимо в плоскости треугольника АВС провести горизонталь и фронталь для того, чтобы построить проекции восстановленного перпендикуляра. Далее из точки С проводим проекции перпендикуляра согласно рассмотренному выше алгоритму о перпендикуляре к плоскости. Для того, чтобы отложить 40 мм, необходимо определить НВ ограниченного отрезка перпендикуляра CF (точку F берем произвольно). НВ отрезка CF определяем методом прямоугольного треугольника на горизонтальной проекции CF. Полученную точку К возвращаем на проекции по теореме Фалеса. Получаем проекции перпендикуляра длиной 40 мм (рисунок. 5.7).
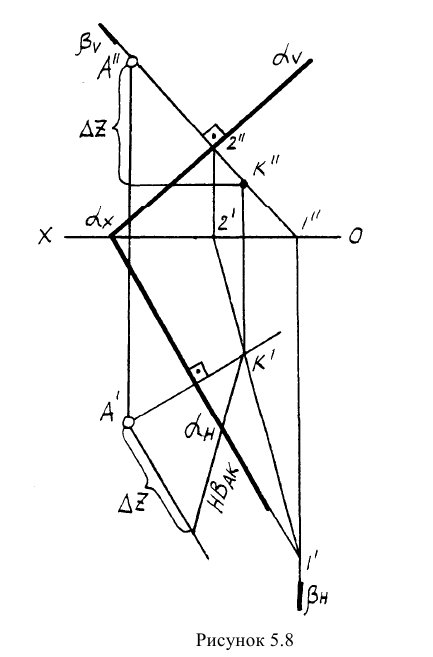
Пример: Найти расстояние от точки А до плоскости, заданной следами
Решение: Из точки А строим перпендикуляр на заданную плоскость. Проекции перпендикуляра проводим перпендикулярно следам. Далее находим точку встречи перпендикуляра с заданной плоскостью с помощью вспомогательной фронтально-проецирующей плоскости 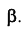
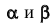
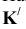
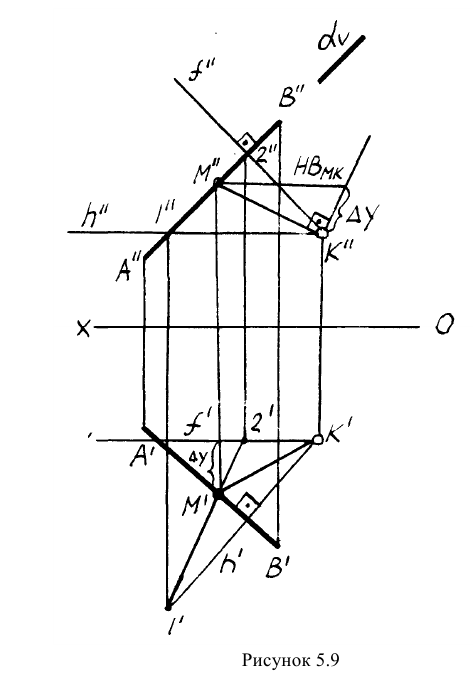
Пример: Определить расстояние от точки К до прямой AВ.
Решение: Через точку К проводим плоскость, перпендикулярную заданной прямой. Плоскость задаем пересекающимися горизонталью и фронталью. Их проекции проводим согласно алгоритму о перпендикуляре к плоскости (обратная задача). Далее находим точку встречи прямой AВ с проведенной плоскостью (точка М). Определяем натуральную величину КМ методом прямоугольного треугольника (рисунок 5.9).
Примеры метрических задач
Задачи, в которых определяются различные геометрические величины -расстояния между объектами, длины отрезков, углы, площади и т.д. называются метрическими. Решение многих метрических задач, например задач на определение кратчайших расстояний, требует построения перпендикулярных прямых и плоскостей.
Перпендикулярность является частным случаем пересечения прямых, прямой и плоскости или двух плоскостей. Необходимо установить соотношения, по которым строятся проекции перпендикулярных прямых и плоскостей.
Теорема о проекциях прямого угла
Прямой угол проецируется на плоскость без искажения, если одна из его сторон параллельна этой плоскости (рис. 10.1).
Рис. 10.1. Теорема о проекциях прямого угла
Дано :
Доказать, что C’A’
Доказательство: если AB||П’, то A’B’||AB, но AA’





На основании этой теоремы две взаимно перпендикулярные прямые (пересекающиеся или скрещивающиеся) проецируются на П1 в виде взаимно перпендикулярных прямых, если одна из них горизонталь, на П2 — если одна из них фронталь (рис. 10.2,а).
Условие перпендикулярности скрещивающихся прямых (рис. 10.2,б) сводятся к условиям перпендикулярности пересекающихся прямых, поведенных через произвольную точку и соответственно параллельных скрещивающимся прямым. Таким образом, понятие перпендикулярности можно отнести как к пересекающимся, так и к скрещивающимся прямым.
Рис. 10.2. Перпендикулярные прямые:
а -пересекающиеся a1 
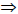

б -скрещивающиеся b2 
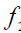

Линии наибольшего наклона плоскости
Прямые, лежащие в плоскости и перпендикулярные линиям уровня этой плоскости, называются линиями наибольшего наклона к соответствующей плоскости проекций (рис. 10.3). Так, прямая, лежащая в плоскости и перпендикулярная горизонтали плоскости, называется линией наибольшего наклона к горизонтальной плоскости проекций, а прямая, перпендикулярная фронтали — линией наибольшего наклона к фронтальной плоскости проекций.
Угол между линией наибольшего наклона и ее проекцией на соответствующую плоскость равен углу наклона плоскости к плоскости проекций (см. рис. 9.15).
Рис. 10.3. Линия наибольшего наклона плоскости а к П1:
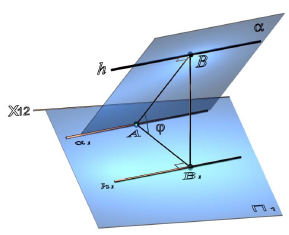
а — плоскость общего положения; h ∈α — горизонталь плоскости а; AB 
φ = 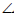
Перпендикулярность прямой и плоскости
Прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым этой плоскости. На основании теоремы о проекциях прямого угла можно получить условие перпендикулярности прямой общего положения и плоскости общего положения:
Если прямая а перпендикулярна плоскости α(ABC), то ее горизонтальная проекция перпендикулярна горизонтальной проекции горизонтали плоскости, а фронтальная проекция — фронтальной проекции фронтали плоскости.
Например, при построении прямой а, перпендикулярной плоскости α(ABC) (рис. 10.4,а), в плоскости строятся линии уровня — горизонталь и фронталь, затем через произвольную точку в плоскости, в данном случае точку K(h×
Рис. 10.4. Перпендикулярность прямой и плоскости:
а -построение прямой, перпендикулярной плоскости:
б -построение плоскости, перпендикулярной прямой:
Аналогично решается задача о построении плоскости, перпендикулярной прямой общего положения (рис. 10.4,б)
Если плоскость проецирующая, проекции линий уровня совпадают со следом плоскости, перпендикулярность устанавливается по отношению к следу плоскости. Горизонтальная проекция перпендикуляра к горизонтально-проецирующей плоскости строится перпендикулярно горизонтальному следу плоскости (рис. 10.5,а). Прямая, перпендикулярная горизонтально-проецирующей плоскости, занимает положение горизонтальной линии уровня.
Аналогично, фронтальная проекция перпендикуляра к фронтально-проецирующей плоскости строится перпендикулярно фронтальному следу плоскости (рис. 10.5,б). Прямая, перпендикулярная фронтально-проецирующей плоскости, занимает положение фронтали.
Рис. 10.5. Перпендикулярность прямой и проецирующей плоскости:
а -построение прямой, перпендикулярной плоскости;
б -построение плоскости, перпендикулярной прямой
Взаимная перпендикулярность плоскостей
Две плоскости взаимно перпендикулярны, если одна из них проходит через перпендикуляр к другой. Таким образом, построение взаимно перпендикулярных плоскостей сводится к построению перпендикулярных прямой и плоскости. Например, чтобы через произвольную точку А провести плоскость, перпендикулярную плоскости a(



Рис. 10.6. Перпендикулярность двух плоскостей
Дано: α(h × 
Построить: A ∈ β 
Решение:
A ∈ n;
Определение метрических задач
Традиционно задачи, связанные с измерением длин, углов, площадей и объемов относят к метрическим. В основе решения этих задач лежит определение длины отрезка и, как производной от этого, площади плоской фигуры.
Определение длины отрезка
Одним из наиболее распространенных методов (рисунок 5.1) является метод прямоугольного треугольника (так его называют в начертательной геометрии) или метод ортогональных дополнений (название, принятое в линейной алгебре).
Идея метода базируется на следующем. Истинная величина отрезка AВ является гипотенузой прямоугольного треугольника, один из катетов которого, является проекцией отрезка AВ на плоскость проекции 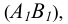
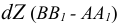
На комплексном чертеже возможно решение как на плоскости 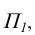
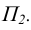
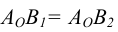
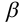
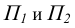
Определение площади треугольника
Определение площади треугольника и величины плоского угла можно свести к известной задаче построения треугольника по трем сторонам.
Для этого достаточно, используя рассмотренный выше способ прямоугольного треугольника, найти по порядку истинные величины сторон 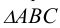
Величина плоского угла между двумя любыми сторонами этой фигуры может быть измерена на истинной величине треугольника.
Проецирование прямого угла
Решение многих задач Начертательной геометрии связано с необходимостью построения на чертеже взаимно перпендикулярных прямых и плоскостей. Базой для этого служит умение строить прямые углы на комплексном чертеже.
Известная в теории чертежа теорема (приведем ее без доказательства) утверждает, что прямой угол (в соответствии с рисунком 5.3) проецируется на
соответствующую плоскость проекций вез искажения, если одна из его сторон параллельна этой плоскости проекций, а вторая — ей не перпендикулярна.
- Заказать чертежи
Перпендикулярность прямых и плоскостей
Выше уже отмечалось, что в трехмерном Евклидовом пространстве отсутствует полная параллельность, то же самое можно сказать и о перпендикулярности. Понятие перпендикулярности так же, как и параллельности, вводится через определение.
Перпендикулярность прямой и плоскости
Считают, что прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся (любым) прямым этой плоскости.
При решении задачи возможны два варианта: проведение перпендикулярной прямой к плоскости из внешней точки и из точки, лежащей в плоскости.
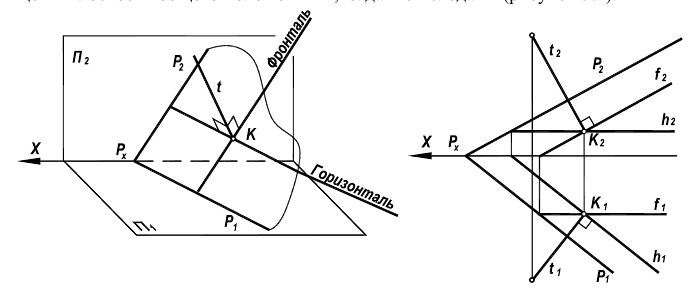
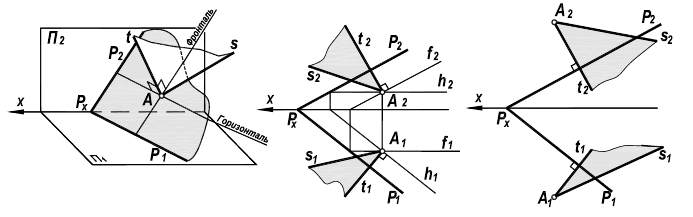
Рассмотрим возможность проведения перпендикуляра из точки К, лежащей в плоскости общего положения Р, заданной следами (рисунок 5.4).
Рисунок 5.4 — Перпендикулярность прямой и плоскости
В плоскости Р (через точку К) проводятся горизонталь h и фронталь f. Прямые, перпендикулярные соответствующим проекциям линий уровня 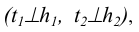
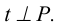
В том случае, когда точка К не лежит в плоскости Р, решение задачи аналогично (рисунок 5.5).
Поскольку положение точки пересечения искомого перпендикуляра не определено, решение соответствует следующей схеме:
а) в плоскости проводятся горизонталь h (через точку В) и фронталь f (через точку A), в случае задания плоскости следами за фронталь и горизонталь принимаются соответствующие следы плоскости
Рисунок 5.5 — Перпендикуляр к плоскости
б) из внешней точки К к соответствующим проекциям линий уровня (следам) проводятся перпендикулярные прямые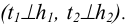
в) определяется точка S пересечения этого перпендикуляра t и плоскости.
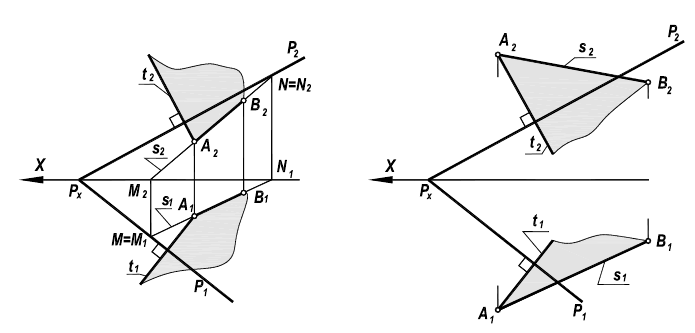
Расстояние от точки до плоскости
Рисунок 5.6 — Расстояние от точки до плоскости
Задачу на определение расстояние от точки до плоскости (рисунок 5.6) можно свести к решению уже известных задач на построение перпендикуляра к плоскости (рисунок 5.5) и определения натуральной величины отрезка прямой (рисунок 5.1)
Перпендикулярность плоскостей
Считают, что две плоскости взаимно перпендикулярны, если одна из них проходит через прямую, перпендикулярную другой плоскости.
Задача может ставиться, как проведение плоскости, перпендикулярной заданной, проходящей через точку или прямую.
При проведении искомой плоскости через точку, как и в предыдущем случае, возможны два варианта проведения плоскости перпендикулярной заданной: через точку, лежащую в плоскости и через точку вне ее (рисунок 5.7).
Точно такой же вариант возникает и при проведении перпендикулярной плоскости через прямую (лежащую в исходной плоскости или не лежащую).
Рассмотрим вариант построения плоскости, проходящей через точку. Пусть точка А лежит в плоскости Р. Линии 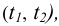
Рисунок 5.7 — Перпендикулярность плоскостей
Проведение через точку А произвольной прямой s позволяет определить плоскость Q, которая будет перпендикулярна плоскости Р.
Если точка А лежит вне плоскости Р, то решение аналогично. Проведение через точку А перпендикуляра t и произвольной прямой s определит плоскость Q, которая также, по определению, будет перпендикулярна плоскости Р.
Решение задачи на проведение плоскости через прямую аналогично решению задачи по проведению плоскости через точку. Достаточно вместо произвольной прямой s использовать заданную прямую АВ. И тогда, в соответствии с рисунком 5.8, задача сведется к проведению перпендикуляра t к плоскости Р (из точки, лежащей в плоскости или лежащей вне ее).
Рисунок 5.8 — Перпендикулярность плоскостей
Определение натуральных величин геометрических элементов
1. Определить натуральную величину отрезка общего положения:
- способом прямоугольного треугольника;
- способом замены плоскостей проекций преобразовать в прямую уровня;
- способом вращения вокруг проецирующей оси преобразовать в прямую уровня.
2. Определить натуральную величину плоскости общего положения (замкнутого отсека):
- способом замены плоскостей проекций преобразовать в плоскость уровня;
- способом вращения вокруг линии уровня преобразовать в плоскость уровня;
- способом плоскопараллельного перемещения преобразовать в плоскость уровня.
Определение расстояния между геометрическими элементами (образами)
1. Определить расстояние от точки до прямой общего положения:
- способом замены плоскостей проекций преобразовать плоскость, заданную прямой и точкой, в плоскость уровня (задачи 3 и 4 преобразования; прямую и точку рассматривать как плоскость);
- способом замены плоскостей проекций преобразовать прямую общего положения в проецирующую прямую (задачи 1 и 2 преобразования);
- способом вращения вокруг линии уровня преобразовать плоскость, заданную прямой и точкой, в плоскость уровня;
- способом плоскопараллельного перемещения преобразовать плоскость, заданную прямой и точкой, в плоскость уровня;
- способом задания плоскости, перпендикулярной к прямой (3-й тип задач), построить через заданную точку плоскость, перпендикулярную к прямой, и определить точку пересечения последней с плоскостью.
2. Определить расстояние между параллельными прямыми:
- способом замены плоскостей проекций преобразовать плоскость, заданную параллельными прямыми, в плоскость уровня (задачи 3 и 4 преобразования);
- способом замены плоскостей проекций преобразовать две параллельные общего положения в проецирующие прямые (задачи 1 и 2 преобразования);
- способом вращения вокруг линии уровня преобразовать плоскость, заданную параллельными прямыми, в плоскость уровня, ограничив ее замкнутым отсеком;
- способом плоскопараллельного перемещения преобразовать плоскость, заданную параллельными прямыми, в плоскость уровня;
- способом задания плоскости, перпендикулярной к прямой (3-й тип задач), построить плоскость через любую точку, принадлежащую одной из прямых, перпендикулярную ко второй прямой, и определить точку пересечения этой плоскости со второй прямой.
3. Определить расстояние между скрещивающимися прямыми, преобразовав одну из прямых в проецирующую (задачи 1 и 2 преобразования).
4. Определить расстояние от точки до плоскости:
- по теме «Перпендикулярность» – провести перпендикуляр к плоскости, построить точку пересечения этого перпендикуляра с заданной плоскостью и найти любым способом натуральную величину построенного отрезка (см. пункт 1);
- способом замены плоскостей проекций преобразовать плоскость общего положения в плоскость проецирующую.
5. Определить расстояние от точки до поверхности вращения:
- способом замены плоскостей проекций преобразовать плоскость, проведенную через точку и ось вращения поверхности, в плоскость уровня (задача 4 преобразования);
- способом вращения вокруг проецирующей оси повернуть плоскость, проведенную через точку и ось вращения поверхности, в плоскость уровня.
Определение углов наклона геометрических элементов к плоскостям проекций H и V
1. Определить углы наклона прямой общего положения к плоскостям проекций H и V:
- способом прямоугольного треугольника построить на двух проекциях натуральные величины отрезка и определить углы наклона прямой;
- способом замены плоскостей проекций преобразовать прямую общего положения в горизонтальную, а затем во фронтальную прямую (задача 1 преобразования);
- способом вращения вокруг соответствующей проецирующей оси преобразовать прямую общего положения в горизонтальную и во фронтальную прямые.
2. Определить угол наклона прямой к заданной плоскости общего положения:
- из любой точки прямой опустить перпендикуляр к плоскости;
- способом вращения вокруг линии уровня преобразовать построенную плоскость, заданную прямой и перпендикуляром, в плоскость уровня;
- искомый угол будет дополнять построенный угол до 90°.
3. Определить величину двухгранного угла, если на чертеже есть линии пересечения плоскостей, образующих двухгранный угол (ребро):
- способом замены плоскостей проекций преобразовать ребро двухгранного угла в проецирующую прямую (задачи 1 и 2 преобразования).
4. Определить угол между двумя плоскостями общего положения, если на чертеже нет линии пересечения заданных плоскостей (ребра):
- задача решается косвенным путем, для чего из любой точки пространства следует опустить перпендикуляры к заданным плоскостям, которые, в свою очередь, задают вспомогательную плоскость, перпендикулярную к этим плоскостям;
- эту вспомогательную плоскость способом вращения вокруг линии уровня следует преобразовать в плоскость уровня, определив угол между перпендикулярами (преобразование вспомогательной плоскости в плоскость уровня возможно и другими способами – ее плоскопараллельным перемещением или заменой плоскостей проекций);
- искомый угол будет дополнять построенный угол до 180° (углом между плоскостями считают угол острый).
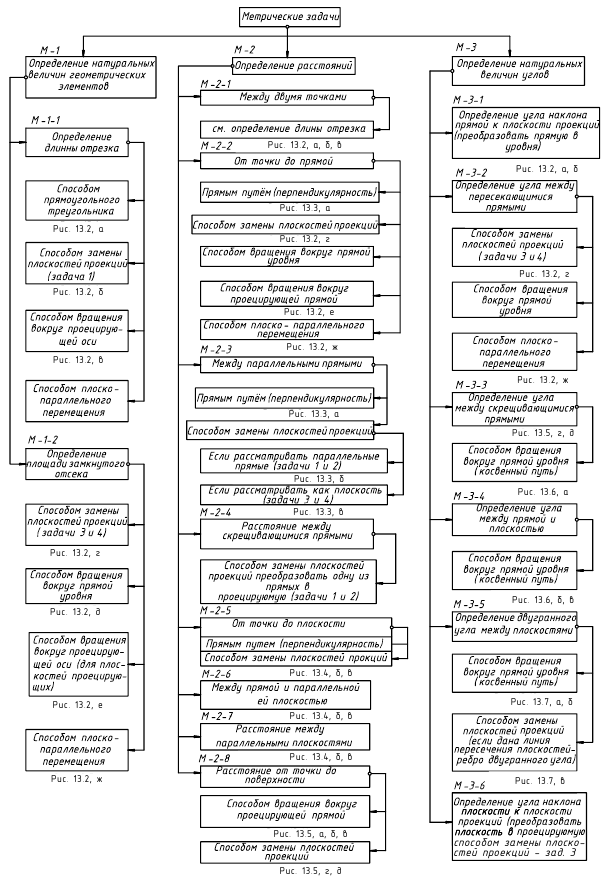
Структуризация материала тринадцатой лекции в рассмотренном объеме схематически представлена на рис. 13.1 (лист 1). На последующих листах 2–7 компактно приведены иллюстрации к этой схеме для визуального повторения изученного материала при его повторении (рис. 13.2–13.7).
Метрические задачи:
Определение натуральной величины геометрических элементов:
1. Определение длины отрезка
Способ прямоугольного треугольника
Способ замены плоскостей проекций (задача 1)
Способ вращения вокруг проецирующей оси
2. Определение площади замкнутого отсека
Способ замены плоскостей проекций (задачи 3 и 4)
Способ вращения вокруг прямой уровня (горизонтали)
Способ вращения вокруг проецирующей оси i(i 
Способ плоско-параллельного перемещения (переноса)
Определение расстояний:
1. Расстояние между точками — определяется величиной отрезка, соединяющего эти точки
См. рис. 13.2, а, б, в
2. Расстояние от точки до прямой — определяется величиной перпендикуляра, опущенного из точки к прямой
а. Прямой путь (перпендикулярность)
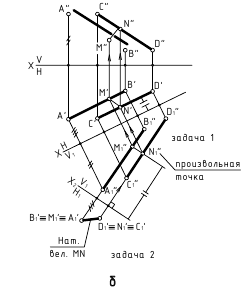
б. Способ замены плоскостей проекций: определить натуральную величину плоскости, которую определяют точка и прямая (см.рис. 13.2, г)
в. Способ вращения вокруг прямой уровня: определить натуральную величину плоскости, которую определяют точка и прямая (см.рис.13.2, д)
г. Способ плоскопараллельного переноса: определить натуральную величину плоскости, которую определяют точка и прямая (см.рис.13.2, ж)
3. Расстояние между параллельными прямыми — определяется величиной перпендикуляра, проведённого из произвольной точки одной прямой к другой прямой
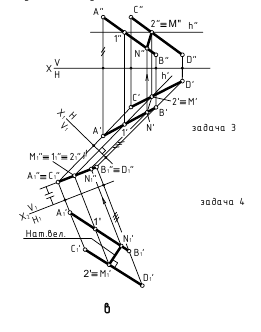
а. Способ замены плоскостей проекции (рассматриваем две прямые) — задачи 1 и 2 (преобразовать прямые общего положения AB и CD в проецирующие)
б. Способ замены плоскостей проекции (рассматриваем плоскость, которую определяют параллельные прямые) — задачи 3 и 4 (определить натуральную величину плоскости ? (AB//СВ))
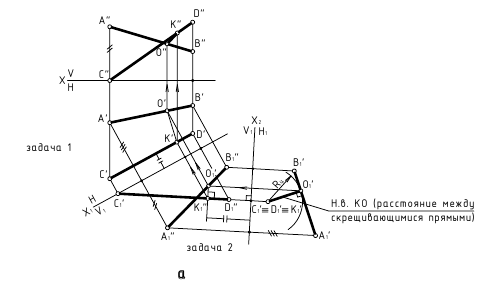
4. Расстояние между скрещивающимися прямыми — определяется величиной перпендикуляра, проведённого от одной из прямых, преобразованной в точку, к другой прямой (задачи 1 и 2 замены плоскостей проекции).
Способ замены плоскостей проекций — задачи 1 и 2
5. Расстояние от точки до плоскости — определяется величиной перпендикуляра, проведённого из точки на плоскость до точки его пересечения с этой плоскостью.
а. Прямой путь (перпендикулярность)
б. Способ замены плоскостей проекций (плоскость преобразовать в проецирующую — задача 3)
6. Расстояние между прямой и параллельной ей плоскостью — определяется величиной перпендикуляра, проведённого из произвольной точки на прямой к плоскости.
См. рис. 13.4, б, в
7. Расстояние между параллельными плоскостями — определяется величиной отрезка перпендикуляра, опущенного из точки одной плоскости на другую плоскость (до точки пересечения с другой плоскостью).
См. рис. 13.4, б, в
8. Расстояние от точки до поверхности
a. Cпособ вращения вокруг проецирующей оси
б. Способ замены плоскостей проекции
Определение величин углов:
1. Угол φ между скрещивающимися прямыми — определяется плоским углом, образованным двумя пересекающимися прямыми, проведёнными из произвольной точки пространства параллельно скрещивающимся прямым (рис. 13.6, а)
Способ вращения вокруг линии уровня
Дано:
а и b — скрещивающиеся прямые
Требуется:
∠φ — ?
Решение:
1.
2. ∠φ — вращением вокруг фронтали, проведённой в построенной плоскости α(d ∩с)
2. Угол φ между прямой и плоскостью — определяется углом между прямой и её проекцией на эту плоскость.
Дано:
α(h ∩ f);
AB — прямая общего положения
Требуется:
∠φ — ?
Решение:
1. l 
l

l

2. ∠φ — вращением вокруг фронтали, проведённой в построенной плоскости β(AB∩l)
3. Угол φ между плоскостями α и β — определяется линейным углом, образованным двумя прямыми, по которым некоторая плоскость γ, перпендикулярная плоскостям (или их ребру), пересекает эти плоскости (углом между плоскостями считают острый угол).
а. Если на чертеже нет ребра (линии пересечения заданных плоскостей) — угол φ определяется способом вращения вокруг линии уровня (рис. а)
Дано:
(m // h); (а ∩ b).
Требуется:
∠φ — ?
Решение:
1. провести в заданной плоскости фронтали и горизонтали;
2. из произвольной точки пространства D (D’, D») провести перпендикуляры l1 и l2 к заданными плоскостям, которые определяют плоскость γ(l1 ∩ l2);
3. ∠φ — вращением вокруг горизонтали h3, проведённой в построенной плоскости γ(l1 ∩ l2).
б. Если на чертеже есть ребро (линия пересечения заданных плоскостей) — угол φ определяется способом замены плоскостей проекций (задачи 1 и 2, рис. б)
Решение:
ребро АВ двугранного угла преобразовать двумя заменами в проецирующую прямую.
- Тени в ортогональных проекциях
- Кривые поверхности
- Пересечения криволинейных поверхностей
- Пересечения поверхностей с прямой и плоскостью
- Пересечение поверхности плоскостью и прямой
- Развертки поверхностей
- Способы преобразования проекций
- Взаимное положение прямой и плоскости
Расстояние от точки до плоскости онлайн
С помощю этого онлайн калькулятора можно найти расстояние от точки до заданной плоскости. Дается подробное решение с пояснениями. Для вычисления расстояния от точки до плоскости введите координаты точки и коэффициенты уравнения плоскости в ячейки и нажимайте на кнопку «Решить».
Предупреждение
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Расстояние от точки до плоскости − теория, примеры и решения
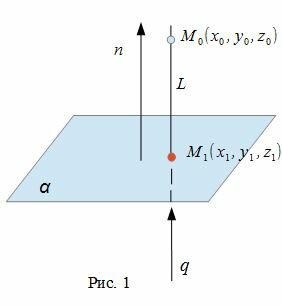
Для нахождения расстояния от точки M0 до плоскости α, необходимо найти расстояние от точки M0 до проекции точки M0 на плоскость α:
Нахождение расстояния от точки до плоскости содержит следующие шаги:
- построение прямой L, проходящей через точку M0 и перпендикулярной плоскости α.
- нахождение точки M1 пересечения плоскости α с прямой L(Рис.1).
- вычисление расстояния между точками M0 и M1.
1. Общее уравнение плоскости имеет вид:
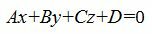 |
(1) |
где n(A,B,C)− называется нормальным вектором плоскости.
Уравнение прямой, проходящей через точку M0(x0, y0, z0) и имеющий направляющий вектор q(l, m, n) имеет следующий вид:
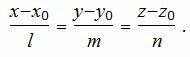 |
(2) |
Для того, чтобы прямая (2) была ортогональна плоскости (1), направляющий вектор q(l, m, n) прямой (2) должен быть коллинеарным нормальному вектору n(A,B,C) плоскости (1)(Рис. 1). Следовательно, в качестве направляющего вектора прямой (2) можно взять нормальный вектор плоскости (1) .
Таким образом, уравнение прямой, проходящей через точку M0(x0, y0, z0) и ортогональной плоскости (1) имеет следующий вид:
 |
(3) |
Для нахождения точку пересечения прямой L с плоскостью α, проще всего рассматривать параметрическое уравнение прямой. Составим ее
Выразим переменные x, y, z через рараметр t.
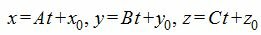 |
(4) |
2. Найдем точку пересечения прямой (4) с плоскостью (1). Для этого нужно найти такой параметр t, при котором точка M(x, y, z) принадлежит плоскости (1). Поэтому подставим значения x,y,z из выражения (4) в (1) и решим относительно t.
A(At+x0)+B(Bt+y0)+C(At+z0)+D=0,
A 2 t+Ax0+B 2 t+By0+C 2 t+Cz0+D=0,
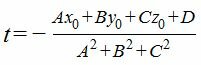 |
(5) |
3. Найдем, наконец, расстояние от точки M0 до плоскости (1). Очевидно, что расстояние от точки M0 до плоскости (1) − это расстояние от точки M0 до точки M1. А это расстояние вычисляется так:
Учитывая значение параметра t, имеем:
Пример 1. Найти расстояние от точки M0(2, -1, -9/31) до плоскости
 |
(7) |
Нормальный вектор плоскости имеет вид:
Подставляя координаты точки M0 и нормального вектора плоскости в (5), получим:
Из выражений (4) находим:
Проекцией точки M0(2, -1, -9/31) на плоскость (7) является точка:
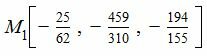
Вычислим расстояние между точками M0 и M1:
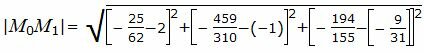
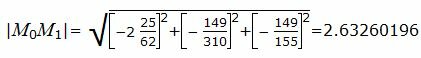
Расстояние от точки M0(2, -1, -9/31) до плоскости (7):
VMath
Инструменты сайта
Основное
Навигация
Информация
Действия
Содержание
Вычисление расстояний между геометрическими объектами
Линейные многообразия
Расстояние от точки до линейного многообразия (плоскости)
Задача. Найти расстояние от точки $ X_ <0>in <mathbb R>^ $ до линейного многообразия (плоскости) $ mathbb M $ в $ <mathbb R>^ $, заданного системой уравнений $$ left< begin c_<11>x_1+c_<12>x_2+dots+c_<1n>x_n &=& h_1 \ dots & & dots \ c_x_1+c_x_2+dots+c_x_n &=& h_m end right. $$ или, в матричном виде $$ CX= <mathcal H>quad npu quad C=left( begin c_<11>& c_ <12>& dots & c_ <1n>\ dots & & & dots \ c_& c_ & dots & c_ end right)_ , <mathcal H>=left( begin h_1 \ vdots \ h_m end right), X=left( begin x_1 \ x_2 \ vdots \ x_n end right) $$ При этом предполагается, что $ mle n_<> $ и что ранг матрицы $ C_<> $ равен $ m_<> $, то есть система уравнений совместна и определяемое ею многообразие в $ <mathbb R>^ $ является $ (n-m)_<> $-мерным.
Теорема 1. [1]. Составим квадратную матрицу порядка $ m+1_<> $:
$$ M=left( begin Ccdot C^ <top>& CX_0- <mathcal H>\ (CX_0- <mathcal H>)^ <top>& 0 end right) $$ Расстояние от точки $ X_ <0>$ до линейного многообразия $ mathbb M $ вычисляется по формуле $$ d= sqrt<-frac<det M><det(Ccdot C^<top>)>> . $$
Доказательство ☞ ЗДЕСЬ.
Расстояние от точки $ X_<0>=(x_<10>,dots,x_)^ <top>$ до гиперплоскости (или, в случае $ n=2 $, прямой)
$$ c_1x_1+dots+c_nx_n= h $$ равно $$ d= frac<|c_1x_<10>+dots+c_nx_-h|><sqrt> . $$ Ближайшая к $ X_0 $ точка гиперплоскости: $$ X_<ast>=X_0- frac+dots+c_nx_-h> left(begin c_1 \ vdots \ c_n end right) , . $$
Пусть теперь линейное многообразие (плоскость) задано параметрически $$ mathbb M= < Y_0+lambda_1 Y_1+dots+lambda_k Y_k quad mid quad <lambda_1,dots,lambda_k>subset <mathbb R>> $$ при фиксированных столбцах $$ \subset <mathbb R>^n . $$ Предположим, что эти столбцы линейно независимы. Составим из них матрицы $$ L=left[ Y_1|dots|Y_k right]_ quad u quad tilde L = left[ Y_1|dots|Y_k| X_0-Y_0 right]_ $$ (здесь $ |_<> $ означает конкатенацию).
Теорема 2. Расстояние $ d_<> $ от точки $ X_ <0>$ до линейного многообразия $ mathbb M $ вычисляется по формуле
Доказательство. Утверждение теоремы 2 является частным случаем общего результата о вычислении расстояния от точки до линейного многообразия в евклидовом пространстве. ♦
Теорема 3. Ближайшая к точке $ X_0 $ точка многообразия $ mathbb M_<> $ (проекция точки на многообразие) определяется по формуле
Доказательство ☞ ЗДЕСЬ.
Пример. Найти расстояние от точки $ X_<0>=(1,1,1,1)^ <top>$ до плоскости
Решение. 1-й способ: применение теоремы 1. Имеем: $$ C=left( begin 3 & 1 & -1 & 1 \ 1 & -2 & 1 & 2 end right), <mathcal H>= left( begin 1 \ 2 end right), $$ $$ Ccdot C^ <top>= left( begin 12 & 2 \ 2 & 10 end right), CX_0=left( begin 4 \ 2 end right), CX_0-<mathcal H>=left( begin 3 \ 0 end right) , $$ $$ frac<left| begin 12 & 2 & 3 \ 2 & 10 & 0 \ 3 & 0 & 0 end right|><left| begin 12 & 2 \ 2 & 10 end right|>=frac<-90><116>=-frac<45> <58> . $$
2-й способ: применение теоремы 2. Общее решение системы уравнений, задающей плоскость: $$ x_3=frac<5><3>x_1+frac<4><3>x_2, x_4=1-frac<4><3>x_1+frac<1><3>x_2 . $$ Таким образом, плоскость может быть представлена в параметрическом виде $$ Y_0+lambda_1 Y_1 + lambda_2 Y_2 quad npu quad Y_0 = left( begin 0 \ 0 \ 0 \ 1 end right), Y_1=left( begin 0 \ 3 \ 4 \ 1 end right), Y_2=left( begin 3 \ 0 \ 5 \ -4 end right) . $$ Имеем: $$ L= left( begin 0 & 3 \ 3 & 0 \ 4 & 5 \ 1 & -4 end right), tilde L =left( begin 0 & 3 & 1 \ 3 & 0 & 1 \ 4 & 5 & 1 \ 1 & -4 & 0 end right), frac<left| begin 26 & 16 & 7 \ 16 & 50 & 8 \ 7 & 8 & 3 end right|><left| begin 26 & 16 \ 16 & 50 end right|>=frac<810><1044>=frac<45> <58> . $$ Координаты ближайшей точки к $ X_ <0>$: $$ X_<ast>= left(begin 1 \ 1 \ 1 \ 1 endright)+left( begin 0 & 3 \ 3 & 0 \ 4 & 5 \ 1 & -4 end right)left( begin 26 & 16 \ 16 & 50 \ end right)^ <-1>left(begin 0 & 3 & 4 & 1 \ 3 & 0 & 5 & -4 end right)left(begin 1 \ 1 \ 1 \ 0 endright)=frac<1> <58>left(begin 16 \ 37 \ 76 \ 49 endright) , . $$
Ответ. $ d=sqrt <45/58>approx 0.8808303295 $.
Расстояние между линейными многообразиями (плоскостями)
Пусть линейные многообразия в $ <mathbb R>^ $ заданы параметрически $$ mathbb M_1= < X_0+ lambda_1 X_1+dots + lambda_k X_k mid <lambda_1,dots,lambda_k >subset mathbb R > ; $$ $$ mathbb M_2=< Y_0+mu_1Y_1+dots+mu_<ell>Y_ <ell> mid <mu_1,dots,mu_<ell>> subset mathbb R > $$ при фиксированных столбцах $$ \>subset <mathbb R>^n . $$ Составим из этих столбцов матрицы $$ P=left[ X_1|dots|X_k| Y_1|dots | Y_ <ell>right]_ quad u quad tilde P = left[ X_1|dots|X_k| Y_1|dots | Y_<ell>| X_0-Y_0 right]_ $$ (здесь $ |_<> $ означает конкатенацию).
Теорема. Расстояние между линейными многообразиями $ mathbb M_1 $ и $ mathbb M_2 $ вычисляется по формуле
Пример. [2]. Найти расстояние между плоскостями
$$ left( begin 89 \ 37 \ 111 \ 13 \54 end right) + lambda_1 left( begin 1 \ 1 \ 0 \ -1 \ -1 end right) + lambda_2 left( begin 1 \ -1 \ 0 \ -1 \ 1 end right) quad mbox < и >quad left( begin 42 \ -16 \ -39 \ 71 \3 end right) + mu_1 left( begin 1 \ 1 \ 0 \ 1 \ 1 end right) + mu_2 left( begin 1 \ -1 \ 0 \ 1 \ -1 end right) . $$
Решение. $$ P^<top>cdot P=4cdot E_<4 times 4>, quad tilde P^<top>cdot tilde P= left(begin 4 & 0 & 0 & 0 & 107 \ 0 & 4 & 0 & 0 & 103 \ 0 & 0 & 4 & 0 & 93\ 0 & 0 & 0 & 4 & -115 \ 107 & 103 & 93 & -115 & 33483 end right) . $$
Ответ. $ d=150_<> $.
Квадратичные многообразия (квадрики)
В последующих пунктах, касающихся вычисления расстояний между геометрическими объектами, хотя бы один из которых представлен квадратным уравнением, используется следующая идеология решения. Первоначальной целью ставится построение уравнения расстояний, т.е. алгебраического уравнения от одной переменной, среди корней которого находится квадрат искомого расстояния. После нахождения этого корня, координаты ближайшей точки (или пары ближайших точек) находятся в виде рациональных функций от величины квадрата расстояния. Таким образом, мы «переворачиваем» традиционную схему решения оптимизационных задач:
стационарные точки $ rightarrow $ критические значения
Такая реверсия традиционного подхода оправдана, с одной стороны, тем, что задача сводится к одномерной — поиску корней полинома от одной переменной. Причем нас будет интересовать, как правило, единственный корень этого полинома — минимальный положительный. С другой стороны, уравнение расстояний удается построить в результате чисто алгебраической процедуры: конечного числа элементарных алгебраических операций над коэффициентами уравнений, задающих многообразия. Алгоритм основан на аппарате исключения переменных в системах нелинейных алгебраических уравнений, и ключевым объектом в нем оказывается вычисление дискриминанта полинома (от одной или двух переменных).
Расстояние от точки до квадрики
Теорема 1. Пусть квадрика в $ <mathbb R>^ $, задана уравнением
$$ X^<top>AX+2B^<top>X-1=0 , (A=A^<top>) . $$ Квадрат расстояния до нее от не лежащей на ней точки $$ X_ <0>in <mathbb R>^, quad ( X_0^<top>AX_0+2 B^<top>X_<0>-1ne 0 ) $$ равен минимальному положительному корню уравнения расстояний $$ <mathcal F>(z)=0 quad npu quad <mathcal F>(z)=<mathcal D>_ <mu>left( Phi(mu,z) right) . $$ Здесь $$ Phi(mu,z)=det left( left[ begin A & B \ B^ <top>& -1 end right] + mu left[ begin -E & X_0 \ X_0^ <top>& z-X_0^<top>X_0 end right] right), $$ $ <mathcal D>_<> $ означает дискриминант полинома $ Phi(mu,z) $, рассматриваемого относительно переменной $ mu_<> $, а $ E_<> $ — единичная матрица порядка $ n_<> $. Дополнительно предполагается, что указанный корень не является кратным.
[3]. Квадрат расстояния от начала координат $ <mathbb O>in <mathbb R>^ $ до квадрики в $ <mathbb R>^ $, заданной уравнением
$$ X^<top>AX+2,B^<top>X-1=0 , $$ равен минимальному положительному корню уравнения расстояний $$ <mathcal F>(z)=0, quad npu quad <mathcal F>(z)=<mathcal D>_ <mu>left( f(mu)(mu z-1)-B^<top>q(A,mu)B right) , $$ и при условии, что указанный корень не является кратным. Здесь $ f(mu_<>)=det (A-mu E) $ — характеристический полином матрицы $ A_<> $, а $ q(A,mu)_<> $ — матрица взаимная матрице $ A-mu E_<> $.
В частном случае $ B=<mathbb O>_<> $ (квадрика центрирована к началу координат), имеем:
$$ <mathcal F>(z)=left[z^nf(1/z) right]^2<mathcal D>_<mu>(f(mu)) , $$ и расстояние от начала координат до квадрики оказывается равным $ 1/sqrt<lambda_<max>^<>> $, где $ lambda_<max>^<> $ — максимальное собственное число матрицы $ A_<> $.
Пример. Найти расстояние от начала координат до эллипсоида
Решение. Здесь $$A = left( <begin frac<7> <18>& -frac<1> <9>& 0 \ && \ -frac<1> <9>& frac<1> <3>& -frac<1> <9>\ && \ 0 & -frac<1> <9>& frac<5> <18>end> right),quad B = left( begin -frac<1> <12>\ \ -frac<1> <9>\ \ frac<5> <36>end right) ,$$ $$ f(mu)=det (A-mu E)=-mu ^ <3>+ mu ^ <2>— frac<11> <36>mu + frac <1> <36>$$ Матрица взаимная матрице $ A-mu E_<> $: $$ q(A, mu)= left( begin mu ^ <2>— frac<11> <18>mu + frac<13> <162>& — frac<1> <9>mu + frac<5> <162>& frac<1> <81>\ && \ — frac<1> <9>mu + frac<5> <162>& mu^2 -frac<2><3>mu+frac<35> <324>& — frac<1> <9>mu +frac<7> <162>\ && \ frac<1> <81>& — frac<1> <9>mu + frac<7> <162>& mu ^ <2>— frac<13><18>mu+frac<19> <162>end right) . $$ $$ Phi(mu,z)=f(mu)(mu z-1)-B^<top>q(A,mu)B= $$ $$ =-z mu ^ <4>+ (z+1) mu ^ <3>+ left(-frac <11> <36>z — frac<673><648>right) mu ^ <2>+left( frac <1> <36>z + frac <241> <729>right) mu — frac <1621> <52488> . $$ Воспользуемся детерминантным представлением дискриминанта: $$ <mathcal F>(z) = <mathcal D>_ <mu>(Phi(mu,z)) = frac<1> <16>times $$ $$ times left| begin 4z & — 3z-3 & frac<11><18>z + frac<673> <324>& — frac<1> <36>z — frac<241> <729>& 0 & 0 \ &&&&& \ 0 & 4z & — 3z-3 & frac<11> <18>z + frac<673> <324>& — frac<1> <36>z — frac<241> <729>& 0 \ &&&&& \ 0 & 0 & 4z & — 3z-3 & frac<11><18>z + frac<673> <324>& — frac<1> <36>z — frac<241> <729>\ &&&&& \ 0 & 0 & — z — 1 & frac<11><18>z + frac<673> <324>& — frac<1> <12>z — frac<241> <243>& frac<1621> <13122>\ &&&&& \ 0 & — z — 1 & frac<11><18>z + frac<673> <324>& — frac<1><12>z — frac<241> <243>& frac<1621> <13122>& 0 \ &&&&& \ — z — 1 & frac<11> <18>z + frac<673> <324>& — frac<1> <12>z — frac<241> <243>& frac<1621> <13122>& 0 & 0 end right| = $$ $$ =2^<-11>3^ <-24>( 38263752,z^6-966487788,z^5+9376985736,z^4-43882396481,z^3+$$ $$ +102982092872,z^2-116747905827,z+50898162294) quad . $$ Вещественные корни уравнения расстояний: $$ z_1approx 1.394685, z_2 approx 5.701814, z_3 approx 7.043941, z_4 approx 7.590060 . $$
Ответ. $ d= sqrt approx 1.180968 $.
Нахождение точки на квадрике, ближайшей к заданной точке $ X_ <0>$, возможно с помощью следующего результата.
Теорема 2. При выполнении условий теоремы 1, координаты точки $ X_ <ast>$ квадрики, ближайшей к точке $ X_ <0>$ находятся по формуле
$$ X_<ast>=-A^ <-1>B — mu_ <ast>(A -mu_<ast>E)^ <-1>(A^ <-1>B+X_0)=(mu_<ast>E- A)^ <-1>(B+mu_ <ast>X_0) . $$ Здесь $ mu_ <ast>$ означает кратный корень полинома $ Phi(mu,z_<ast>) $, где полином $ Phi(mu,z) $ берется из формулировки теоремы 1, а $ z_<ast>^<> $ означает минимальный положительный корень уравнения расстояний.
Этот результат требует пояснений. Итак, поскольку дискриминант полинома $ Phi(mu,z_<ast>) $ обращается в нуль, то у этого полинома — как полинома по $ mu_<> $ — имеется кратный корень $ mu =mu_ <ast>$. Можно доказать [4], что при условии простоты корня $ z=z_ <ast>$ уравнения расстояний $ mathcal F(z)=0 $ кратность корня $ mu =mu_ <ast>$ для полинома $ Phi(mu,z_<ast>) $ будет равна ровно $ 2_<> $, и других кратных корней этот полином не имеет. Но тогда, выражение для $ mu_<ast>^<> $ может быть найдено в виде рациональной функции коэффициентов полинома $ Phi(mu,z_<ast>) $. Последнее утверждение может быть доказано разными способами, и в качестве самого наглядного выберем тот, что основан на свойствах дискриминанта, например, на том, что изложено ☞ ЗДЕСЬ.
При выполнении условия предыдущей теоремы, координаты точки $ X_<ast>^<> $, ближайшей на квадрике к точке $ X_ <0>$, являются рациональными функциями от квадрата расстояния.
Точка $ X_ <ast>$ квадрики $ X^<top>AX+2,B^<top>X-1=0 $, ближайшая к началу координат $ X_0= mathbb O $, находится по формуле:
$$ X_ <ast>= — frac<1>)> q(A,mu_<ast>) B . $$ Здесь $ f(mu_<>)=det (A-mu E) $ — характеристический полином матрицы $ A_<> $, $ q(A,mu)_<> $ — матрица взаимная матрице $ A-mu E_<> $, а $ mu_ <ast>$ означает кратный корень уравнения $$f(mu)(mu z_<ast>-1)-B^<top>q(A,mu)B=0 , $$ где $ z_<ast>^<> $ — величина квадрата расстояния от $ mathbb O_<> $ до квадрики.
Пример. Найти ближайшую к началу координат точку эллипсоида из предыдущего примера.
Решение. Подставляем $ z_<>=z_ <ast>approx 1.394685 $ в формулу для определения кратного корня, т.е. в отношение двух конкретных миноров детерминантного представления дискриминанта: $$ mu=-frac<left| begin 4z & — 3z-3 & frac<11> <18>z + frac<673> <324>& 0 \ &&& \ 0 & 4z & — 3z-3 & — frac<1> <36>z — frac<241> <729>\ &&& \ 0 & — z — 1 & frac<11><18>z + frac<673> <324>& frac<1621> <13122>\ &&& \ — z — 1 & frac<11><18>z + frac<673> <324>& — frac<1><12>z — frac<241> <243>& 0 end right|> <left| begin 4z & — 3z-3 & frac<11> <18>z + frac<673> <324>& — frac<1> <36>z — frac<241> <729>\ &&& \ 0 & 4z & — 3z-3 & frac<11><18>z + frac<673> <324>\ &&& \ 0 & — z — 1 & frac<11><18>z + frac<673> <324>& — frac<1><12>z — frac<241> <243>\ &&& \ — z — 1 & frac<11><18>z + frac<673> <324>& — frac<1><12>z — frac<241> <243>& frac<1621> <13122>end right|> $$ получаем $ mu_<ast>^<> approx 0.572670 $. Подставляем это значение в формулу для определения $ X_<ast>^<> $ из последнего следствия: $$ X_<ast>approx left(begin 0.071171 \ -0.867719 \ 0.797924 end right) . $$
Проверка. Если подставить вместо $ X_ <ast>$ его приближенное значение, то получим: $$ X_<ast>^ <top>X_ <ast>approx mathbf<1.39468>4, X_<ast>^<top>AX_<ast>+2,B^<top>X_<ast>-1 approx 2.9cdot 10^<-5> , $$ и вектор $ <mathbb O>X_ <ast>$ перпендикулярен эллипсоиду в точке $ X_<>=X_ <ast>$: $$ AX_<ast>+B approx left(begin 0.040757\ -0.496917 \ 0.456948 end right)approx mu_ <ast>X_ <ast> . $$
Расстояние от линейного многообразия (плоскости) до квадрики
Задача. Найти расстояние от эллипсоида в $ <mathbb R>^ $, заданного уравнением $$ X^<top>AX+2B^<top>X-1=0 , (A=A^<top>) $$ до линейного многообразия (плоскости) в $ <mathbb R>^ $, заданной системой уравнений $$ left< begin c_<11>x_1+c_<12>x_2+dots+c_<1n>x_n &=& 0 \ dots & & dots \ c_x_1+c_x_2+dots+c_x_n &=& 0 end right. iff CX= <mathbb O>quad npu quad C=left( begin c_<11>& c_ <12>& dots & c_ <1n>\ dots & & & dots \ c_& c_ & dots & c_ end right)_ $$ При этом предполагается, что $ mle n_<> $ и что ранг матрицы $ C_<> $ равен $ m_<> $, т.е. определяемая системой плоскость в $ <mathbb R>^ $ является $ (n-m)_<> $-мерной.
Теорема. [3]. Необходимое и достаточное условие того, что линейное многообразие (плоскость) пересекает эллипсоид зависит от знакоопределенности матрицы $ A_<> $:
Условие равенства нулю определителя из теоремы является необходимым и достаточным для существования точки касания эллипсоида и плоскости.
Теорема. [3]. Если условие предыдущей теоремы не выполняется, то квадрат расстояния от эллипсоида до плоскости совпадает с минимальным положительным корнем полинома
$$ <mathcal F>(z) =<mathcal D>_mu left( mu^m left| begin A & B & C^<top>\ B^ <top>& -1 + mu z & mathbb\ C & mathbb & frac<1> <mu>C cdot C^ <top>end right| right), $$ в предположении, что этот корень не является кратным. Здесь $ <mathcal D>_<> $ — дискриминант полинома, рассматриваемого относительно переменной $ mu_<> $.
Если строки матрицы $ C_<> $ ортонормированны, то преобразованием определителя в теореме можно понизить его порядок: выражение под знаком дискриминанта можно преобразовать в
Пример. Найти расстояние от оси $ <mathbb O>x_ <1>$ до эллипсоида
$$ 7, x_1^2+6, x_2^2 +5, x_3^2 -4,x_1x_2-4,x_2x_3-37,x_1-12,x_2+3,x_3+54=0 . $$
Решение. Здесь $$ A= left( begin -frac<7> <54>& frac<1> <27>& 0 \ &&\ frac<1> <27>& -frac<1> <9>& frac<1> <27>\ &&\ 0 & frac<1> <27>& -frac<5> <54>end right), B=left( begin frac<37> <108>\ \ frac<1> <9>\ \ -frac<1> <36>end right) $$ и можно взять $$ C= left( begin 0 & 1 & 0 \ 0 & 0 & 1 end right) . $$ Матрица $ A_<> $ отрицательно определена, условие пересечения прямой и эллипсоида не выполняется: $$ left| begin A & B & C^<top>\ B^ <top>& -1 & <mathbb O>\ C & <mathbb O>& mathbb end right| times (-1)^3 = — frac <143>
Расстояния в $ <mathbb R>^ $ от плоскости
$$ c_1x_1+dots+c_nx_n = h iff CX=h $$ до ближайшей и до самой дальней точек эллипсоида $$ X^<top>AX+2B^<top>X-1=0 , (A=A^<top>) $$ совпадают с модулями корней полинома: $$ <mathcal F>(Z)=left| begin A & B & C^<top>/|C|\ B^ <top>& -1 & Z-h/|C|\ C/|C| & Z-h/|C| & 0 end right| . $$ Здесь $ |C|=sqrt> $ и предполагается, что поверхности не пересекаются.
Пример. Найти расстояние от прямой $ 2, x_1- x_<2>=0 $ до эллипса
$$ 7,x_1^2-4,x_1x_2 + 6, x_2^2-47, x_1 -24, x_ <2>+124 = 0 .$$
Решение. Здесь $$ <mathcal F>(Z)=left| begin A & B & C^<top>/|C| \ B^ <top>& -1 & Z-h/|C| \ C/|C| & Z-h/|C| & 0 end right| = left| begin -frac<7> <124>& frac<1> <62>& frac<47> <248>& frac<2><sqrt<5>> \ &&& \ frac<1> <62>& — frac<3> <62>& frac<3> <31>&- frac<1><sqrt<5>> \ &&& \ frac<47> <248>& frac<3> <31>& -1 & Z \ &&& \ frac<2><sqrt<5>> & — frac<1><sqrt<5>> & Z & 0 end right| = $$ $$ =-frac<1><307520>left(760,Z^2+1592sqrt<5>, Z+2383 right) $$ и корни этого полинома: $$ -frac<199><190>sqrt<5>pm frac<1> <76>sqrt <13570> . $$
Ответ. $$ d = left| -frac<199><190>sqrt<5>+ frac<1> <76>sqrt <13570>right| approx 0.809219_<> . $$
Расстояние между квадриками
Теорема. Пусть $ X^ <top>A_ <1>X =1 $ и $ X^ <top>A_ <2>X =1 $ – квадрики в $ <mathbb R>^ $, причем первая является эллипсоидом. Квадрики не пересекаются тогда и только тогда, когда матрица $ A_<1>-A_2 $ является знакоопределенной.
Доказательство ☞ ЗДЕСЬ.
Теорема. [3,4]. Если выполняется условие предыдущей теоремы, то квадрат расстояния между
$$ mbox <эллипсоидом> X^ <top>A_ <1>X =1 mbox<и квадрикой> X^ <top>A_ <2>X =1 $$ совпадает с минимальным положительным корнем уравнения расстояний $$ <mathcal F>(z)=0 quad npu quad <mathcal F>(z)=<mathcal D>_ <lambda>left( Phi(lambda,z) right) . $$ Здесь $$ Phi(lambda,z)=det (lambda A_1 + (z- lambda) A_2 — lambda (z-lambda) A_1 A_2), $$ $ <mathcal D>_<> $ — дискриминант полинома рассматриваемого относительно переменной $ lambda_<> $. Дополнительно предполагается, что указанный корень не является кратным.
Пример. Найти расстояние между эллипсами
$$10,x_1^2-12,x_1x_2+8,x_2^2=1 qquad u qquad x_1^2+x_1x_2+x_2^2=1 . $$
Решение. Здесь $$ A_1= left( begin 10 & — 6 \ -6 & 8 end right), quad A_2= left( begin 1 & frac<1> <2>\ frac<1> <2>& 1 end right) $$ и матрица $ A_<1>-A_2 $ положительно определена. Следовательно эллипсы не пересекаются. $$ Phi(lambda,z)=det (lambda A_1 + (z- lambda) A_2 — lambda (z-lambda) A_1 A_2)= $$ $$ =33,lambda^4+left(-66z+frac<149><2>right)lambda^3+left(33,z^2-61,z+frac<83><4>right)lambda^2+left(-frac<27><2>z^2+frac<45><2>zright)lambda+frac<3><4>,z^2 $$ и дискриминант этого полинома по переменной $ lambda_<> $ равен $$ <mathcal F>(z)=frac<3><16>z^2 (<scriptstyle 936086976>, z^6-<scriptstyle 10969697376>,z^5+ <scriptstyle 50706209664>, z^4 —<scriptstyle 115515184664>, z^3+<scriptstyle 130176444432>, z^2 —<scriptstyle 59826725574>,z+<scriptstyle 2866271785>) . $$ Положительные корни уравнения расстояний $ <mathcal F>(z)=0 $: $$ z_1 approx 0.053945666, z_2 approx 1.3340583883, z_3 approx 1.95921364, z_4 approx 2.8785867381 . $$
Ответ. $ d_<>= sqrt approx 0.23226206 $.
Нахождение координат ближайших точек на квадриках (обеспечивающих найденное расстояние) возможно по алгоритму:
1. Если $ z=z_ <ast>$ — корень полинома $ <mathcal F>(z) $, то это значит, что полином $$ Phi(lambda, z_<ast>) = det ( lambda A_1 +(z_<ast>-lambda)A_2 — lambda (z_<ast>-lambda) A_2A_1) $$ имеет кратный корень $ lambda_<> = lambda_ <ast>$. При выполнении условий теоремы, этот корень будет единственным второй кратности и его можно выразить в виде рациональной функции от $ z_ <ast>$ с помощью субдискриминантов.
2. Столбец координат $ X_<ast>^<> $ точки первой квадрики, удовлетворяет тогда однородной системе уравнений $$ ( lambda_ <ast>A_1 +(z_<ast>-lambda_<ast>)A_2 — lambda_ <ast>(z_<ast>-lambda_<ast>) A_2A_1) X = mathbb O , $$ которая имеет бесконечное множество решений, поскольку определитель ее матрицы равен нулю. Из этого бесконечного множества мы выделяем те решения, что удовлетворяют условию $ X^<top>A_<1>X=1 $.
При выполнении условий теоремы таких решений будет два (что соответствует симметрии задачи, см. рисунок).
Аналогично, столбец координат $ Y_<ast>^<> $ точки на второй квадрике $ Y^<top>A_<2>Y=1_<> $ будет решением системы уравнений $$ ( lambda_ <ast>A_1 +(z_<ast>-lambda_<ast>)A_2 — lambda_ <ast>(z_<ast>-lambda_<ast>) A_1A_2) Y = mathbb O . $$
Для нахождения решений воспользуемся одним из результатов теории систем линейных уравнений. Составим столбец из алгебраических дополнений к элементам какой-либо строки матрицы $$ M= lambda_ <ast>A_1 +(z_<ast>-lambda_<ast>)A_2 — lambda_ <ast>(z_<ast>-lambda_<ast>) A_2A_1 . $$ Тогда вектор $ X_<ast>^<> $ отличается от этого столбца лишь множителем, который определится из условия $ X^<top>A_<1>X=1_<> $. Аналогично, для получения столбца координат $ Y_<ast>^<> $ возьмем столбец из алгебраических дополнений к элементам какого-либо столбца той же матрицы $ M_<> $ и домножим его на константу, чтобы обеспечить выполнение условия $ Y^<top>A_<2>Y=1_<> $.
3. Получившиеся пары $ X_<ast>,Y_<ast>^<> $ надо согласовать: они должны подчиняться условию $$ (X_<ast>-Y_<ast>)^<top>(X_<ast>-Y_<ast>)=z_ <ast> . $$
Пример. Найти ближайшие точки эллипсов из предыдущего примера.
Решение. Для найденного значения $ z_<ast>=z_1 approx 0.053945666_<> $ определитель матрицы $$ M=left( begin 7,lambda^2+(-7z+9)lambda+z & -2lambda^2+(2,z-frac<13><2>)lambda+frac<1><2>z \ & \ -lambda^2+(z-frac<13><2>)lambda+frac<1><2>z & 5lambda^2+(-5z+7)lambda+z end right) $$ как полином по $ lambda_<> $ будет иметь кратный корень. Этот корень определяем 1) с помощью субдискриминантов в виде: $$ lambda=-frac<-725274,z^5+1455894,z^4+frac<11286981><2>z^3-frac<26486523><2>z^2+frac<42000075><8>z> <17591706,z^4-109992894,z^3+frac<450450691><2>z^2-frac<315606253><2>z+frac<77466805><8>> . $$ Подстановка сюда $ z=z_<ast>^<> $ даст $ lambda_ <ast>approx -0.13576051_<> $.
Далее, при найденных значениях $ z_<> $ и $ lambda_<> $ система линейных уравнений $$ MX=mathbb O_ <2times 1>$$ должна иметь бесконечное множество решений относительно вектора $ X_<2times 1>^<> $. Одно из этих решений может быть построено (см. упражнение ☞ ЗДЕСЬ ) с помощью алгебраических дополнений к элементам, например, второй строки матрицы $ M_<> $: $$ left( begin 2lambda^2-(2,z-frac<13><2>)lambda-frac<1><2>z \ \ 7,lambda^2+(-7z+9)lambda+z end right) quad begin longrightarrow \ z=z_<ast>, lambda= lambda_ <ast>end quad X=left( begin -0.8579069 \ \ -0.9876166 end right) . $$ Любое другое решение получается домножением полученного на произвольную константу («растяжением» вектора). Воспользуемся этим, чтобы добиться выполнения условия $ X^<top>A_ <1>X =1_<> $. $$ X_<ast>=frac<1><sqrtA_1 X>> X approx left( begin -0.3838312 \ -0.4418639 end right) . $$ Аналогично, для нахождения точки на другом эллипсе, мы решаем систему $$ M^<top>Y=mathbb O_ <2times 1> , $$ представив ее решение опять-таки с помощью алгебраических дополнений к элементам второго столбца матрицы $ M_<> $: $$ left( begin lambda^2-(z-frac<13><2>)lambda-frac<1><2>z \ \ 7,lambda^2+(-7z+9)lambda+z end right) quad begin longrightarrow \ z=z_<ast>, lambda= lambda_ <ast>end quad left( begin -0.8836615 \ \ -0.9876166 end right) quad Rightarrow quad Y_ <ast>approx left( begin -0.5449964 \ \ -0.6091105 end right) . $$
Ответ. $ pm (0.3838312,, 0.4418639)_<> $ и $ pm (0.5449964,, 0.6091105)_<> $ соответственно (знаки должны быть согласованы).
Проверка. Если в ответе взять знак $ +_<> $: $$ X_<ast>-Y_ <ast>= left( begin -0.1611652 \ -0.1672466 end right)= lambda_ <ast>A_1X_<ast>=(lambda_<ast>-z_<ast>)A_2Y_<ast>,quad (X_<ast>-Y_<ast>)^<top>(X_<ast>-Y_<ast>)approx mathbf<0.0539456>4 . $$
Теорема. [3,4].Пусть
$$ X^ <top>A_<1>X+2,B^<top>_1X-1=0 mbox <и> X^ <top>A_<2>X+2,B^<top>_2X-1=0 $$ — квадрики в $ <mathbb R>^_<> $, причем первая является эллипсоидом. Квадрики пересекаются тогда и только тогда, когда среди вещественных корней полинома
$$ Theta (z) = <mathcal D>_lambda left( det left( left[ begin A_2 & B_2\ B_2^ <top>& -1-z end right] — lambda left[ begin A_1 & B_1\ B_1^ <top>& -1 end right] right) right) $$ имеются числа разных знаков или нуль. Здесь $ <mathcal D>_<> $ — дискриминант полинома рассматриваемого относительно переменной $ lambda_<> $.
Для того, чтобы существовала точка касания квадрик
$$ X^ <top>A_<1>X+2,B^<top>_1X-1=0 mbox <и> X^ <top>A_<2>X+2,B^<top>_2X-1=0 $$ необходимо и достаточно, чтобы было выполнено условие $$ <mathcal D>_lambda left( det left( left[ begin A_2 & B_2\ B_2^ <top>& -1 end right] — lambda left[ begin A_1 & B_1\ B_1^ <top>& -1 end right] right) right) =0 . $$
Теорема. [3,4]. Если не выполняется условие предыдущей теоремы, то квадрат расстояния между
$$ mbox <эллипсоидом>quad X^ <top>A_<1>X+2,B^<top>_1X-1=0 quad mbox < и квадрикой >quad X^ <top>A_<2>X+2,B^<top>_2X-1=0 $$ совпадает с минимальным положительным корнем полинома $$ <mathcal F>(z) = $$ $$ =<mathcal D>_ <mu_1, mu_2>left( det left( mu_1 left[ begin A_1 & B_1\ B_1^ <top>& -1 end right] + mu_2 left[ begin A_2 & B_2\ B_2^ <top>& -1 end right] — left[ begin A_2 A_1 & A_2 B_1\ B_2^ <top>A_1 & B_2^<top>B_1 — mu_1 mu_2 z end right] right) right), $$ в предположении, что этот корень не является кратным. Здесь $ <mathcal D>_<> $ — дискриминант полинома рассматриваемого относительно переменных $ mu_<1>, mu_ <2>$.
Пример. Найти расстояние между эллипсами
Ответ. $ d approx sqrt <9.0183982802>approx 3.00306481 $.
Нахождение ближайших точек на квадриках (обеспечивающих найденное расстояние) возможно по следующему алгоритму.
2. Составим матрицу $$ M= mu_ <1ast>A_1+mu_<2ast>A_2-A_2A_1 . $$ Тогда координатные столбцы ближайших точек на квадриках вычисляются по формулам: $$ X_<ast>=M^ <-1>(A_2B_1-mu_ <1ast>B_1-mu_<2ast>B_2), Y_<ast>=(M^<-1>)^<^<top>> (A_1B_2 — mu_ <1ast>B_1-mu_<2ast>B_2). $$
Пример. Найти ближайшие точки эллипсов из предыдущего примера.
Ответ. $$ X_<ast>approx left(begin -0.4824707833 \ 1.1065143947 end right), Y_<ast>approx left( begin -3.46262940675\ 0.73630788509 end right) . $$
Проверка. $$ (X_<ast>-Y_<ast>)^<top>(X_<ast>-Y_<ast>)approx mathbf<9.018398280>3 , $$ $$ X_<ast>^<top>A_1X_<ast>+2B_1^<top>X_<ast>-1 approx 1cdot 10^<-9> , Y_<ast>^<top>A_2Y_<ast>+2B_2^<top>Y_<ast>-1approx -3cdot 10^<-10> , $$ и вектор $ X_<ast>-Y_<ast>^<> $ перпендикулярен обоим эллипсам в соответствующих ближайших точках: $$ A_1X_<ast>+B_1= left(begin 1.767863990 \ 0.219610712 end right)=mu_ <2ast>(X_<ast>-Y_<ast>), A_2Y_<ast>+B_2= left(begin -0.1254448880 \ -0.0155832356 end right)=-mu_ <1ast>(X_<ast>-Y_<ast>) . $$
Пример. Найти расстояние между эллипсоидами
$$ 7,x_1^2+6,x_2^2+5,x_3^2-4,x_1x_2-4,x_2x_3-37,x_1-12,x_2+3,x_3+54=0$$ и $$ 189,x_1^2+x_2^2+189,x_3^2+2,x_1x_3-x_2x_3-27=0 .$$
Ответ. $ d approx sqrt <1.3537785005>approx 1.1635198754_<> $
Алгебраические кривые и многообразия
Расстояние от точки до плоской алгебраической кривой
Задача. Пусть алгебраическая кривая задана уравнением $$ Phi(x,y)=0 . $$ Здесь $ Phi_<>(x,y) $ — отличный от константы полином от $ x_<> $ и $ y_<> $ с вещественными коэффициентами. Требуется найти расстояние до этой кривой от начала координат.
Здесь возникает проблема, которую для рассмотренных выше случаев удавалось либо обойти, либо же сравнительно дешево решить: это проблема существования решения. Дело в том, что уравнение может не иметь вещественных решений, то есть не определять никакой кривой на плоскости $ mathbb R^ <2>$.
Будем решать задачу сначала для частного случая — пусть полином $ Phi_<>(x,y) $ является четным по переменной $ y_<> $. Геометрически это означает, что кривая (если она существует) будет зеркально симметричной относительно оси $ mathbb Ox $. А с аналитической точки зрения такой полином можно представить в виде полинома $$ F(x,Y) equiv Phi_<>(x,y) quad npu quad Y=y^2 . $$
Теорема 1 [6]. Пусть $ Phi_<>(x,y) equiv Phi_<>(x,-y) $. Уравнение $ Phi_<>(x,y)=0 $ не имеет вещественных решений если одновременно выполняются два условия:
a) уравнение $ Phi(x,0)=0 $ не имеет вещественных решений;
б) уравнение $$ mathcal F(z)=mathcal D_x( F(x,z-x^2))=0 $$ не имеет положительных решений.
Если хотя бы одно из этих условий не выполняется, то квадрат расстояния от начала координат до кривой $ Phi(x_<>,y)=0 $ равен либо квадрату минимального по модулю вещественного корня уравнения $ Phi(x,0)=0 $, либо же минимальному положительному корню уравнения $ mathcal F(z)= 0 $, при условии, что последний не является кратным. Здесь $ <mathcal D>_<> $ — дискриминант полинома, рассматриваемого относительно переменной $ x_<> $.
Пример. Найти расстояние от начала координат до кривой
Решение. Уравнение $$ Phi(x,0)=x^6-6,x^5+25,x-45=0 $$ имеет вещественные корни $ mu_1approx -1.621919 $ и $ mu_2 approx 5.986387 $. 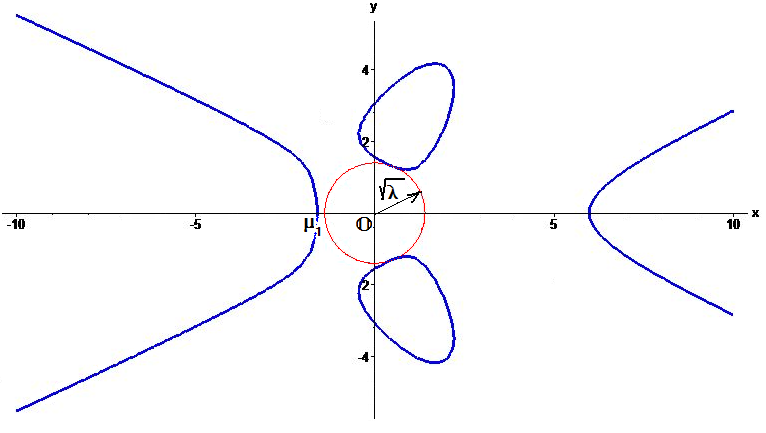
Пример. В точках $ P_<1>,P_2,P_3 $ расположены источники полезных ископаемых: железной руды, угля и воды соответственно. Известно, что для производства одной тонны стали необходимо иметь $ m_ <1>$ тонн руды, $ m_2 $ тонн угля и $ m_3 $ тонн воды. В предположении, что стоимость перевозки одной тонны груза не зависит от его природы, где следует расположить сталелитейное производство так, чтобы минимизировать транспортные издержки?
Подробное обсуждение этой задачи (и к ней примыкающих) ☞ ЗДЕСЬ.
Задача о точке Лемуана-Греба
Задача. Найти точку плоскости, cумма квадратов расстояний от которой до сторон треугольника, лежащего в этой же плоскости, минимальна.
Решение. Пусть $ d_1, d_2,d_3 $ — расстояния от точки $ P_<> $ плоскости до сторон треугольника с длинами $ D_1, D_2, D_3 $ соответственно. Воспользуемся тождеством Лагранжа: $$ (d_1^2+ d_2^2+d_3^2)(D_1^2+ D_2^2+D_3^2)equiv $$ $$ equiv (d_1D_1+ d_2D_2+d_3D_3)^2+(d_1D_2-d_2D_1)^2+(d_2D_3-d_3D_2)^2+ (d_1D_3-d_3D_1)^2 . $$ Величина $ d_1D_1+ d_2D_2+d_3D_3 $ является постоянной, не зависящей от координат точки $ P_<> $: $$ d_1D_1+ d_2D_2+d_3D_3 =2S , $$ где $ S_<> $ — площадь данного треугольника. Следовательно $ min (d_1^2+d_2^2+d_3^2) $ достигается при условиях $$ d_1D_2-d_2D_1=0, d_2D_3-d_3D_2=0, d_1D_3-d_3D_1=0 , $$ то есть когда $$ frac=frac=frac . $$ Определяемая этими соотношениями точка называется точкой Лемуана 6) или точкой Греба 7) ; в ней пересекаются симедианы треугольника.
Еще некоторые задачи
Построение прямой на плоскости, сумма квадратов расстояний до которой от заданных точек минимальна ☞ ЗДЕСЬ
Расстояние от точки до плоскости
Формула для вычисления расстояния от точки до плоскости
Если задано уравнение плоскости A x + B y + C z + D = 0 , то расстояние от точки M(M x , M y , M z ) до плоскости можно найти, используя следующую формулу:
| d = | |A·M x + B·M y + C·M z + D| |
| √ A 2 + B 2 + C 2 |
Примеры задач на вычисление расстояния от точки до плоскости
Решение. Подставим в формулу коэффициенты плоскости и координаты точки
d = |2·0 + 4·3 + (-4)·6 — 6| √ 4 + 16 + 16 = |0 + 12 — 24 — 6| √ 36 = |-18| 6 = 3
Ответ: расстояние от точки до плоскости равно 3.
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
источники:
http://vmath.ru/vf5/algebra2/optimiz/distance
http://ru.onlinemschool.com/math/library/analytic_geometry/p_plane/
Нужно добиться следующего результат, как показано на рисунке
Известны координаты красной точки и координаты (широта/долгота) на сфере (из можно конвертировать в мировые (3D)
Если провести прямую до нужной точки, то в случае ее нахождения по ту сторону сферы прямая будет пересекать сферу. Конечно, можно было бы перевести первую точку пересечения в координаты сферы и уже по широте/долготе найти расстояние и прибавить его к расстоянию к первой точке, но так расстояние будет преувеличеным, если точка находится ровно с обратной стороны.
UPD:
осталось разобраться как найти точку касательной к сфере