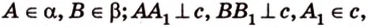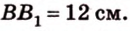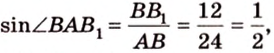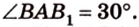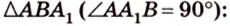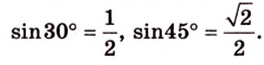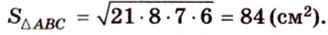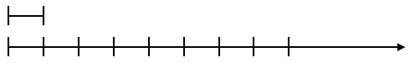Время на прочтение
6 мин
Количество просмотров 137K
Вступление
Это вторая часть моей статьи посвящена вычислительной геометрии. Думаю, эта статья будет интереснее предыдущей, поскольку задачки будут чуть сложнее.
Начнем с взаимного расположения точки относительно прямой, луча и отрезка.
Задача №1
Определить взаимное расположении точки и прямой: лежит выше прямой, на прямой, под прямой.
Решение
Понятно, что если прямая задана своим уравнением ax + by + c = 0, то тут и решать нечего. Достаточно подставить координаты точки в уравнение прямой и проверить чему оно равно. Если больше нуля, то точка находится в верхней полуплоскости, если равна нулю, то точка находится на прямой и если меньше нуля, то точка находится в нижней полуплоскости. Интереснее случай, когда прямая задана, задана координатами двух точек назовем их P1(x1, y1), P2(x2, y2). В этом случае можно спокойно найти коэффициенты a, b и c и применить предыдущее рассуждение. Но надо сначала подумать, оно нам надо? Конечно, нет! Как я говорил косое произведения — это просто жемчужина вычислительной геометрии. Давайте применим его. Известно, что косое произведение двух векторов положительно, если поворот от первого вектора ко второму идет против часовой стрелки, равно нулю, если векторы коллинеарны и отрицательно, если поворот идет по часовой стрелки. Поэтому нам достаточно посчитать косое произведение векторов P1P2 и P1M и по его знаку сделать вывод.
Задача №2
Определить принадлежит ли точка лучу.
Решение
Давайте вспомним, что такое луч: луч — это прямая, ограниченная точкой с одной стороны, а с другой стороны бесконечная. То есть луч задается некоторой начальной точкой и любой точкой лежащей на нем. Пусть точка P1(x1, y1) — начало луча, а P2(x2, y2) — любая точка принадлежащая лучу. Понятно, что если точка принадлежит лучу, то она принадлежит и прямой проходящей через эти точки, но не наоборот. Поэтому принадлежность прямой является необходимым, но не достаточным условием для принадлежности лучу. Поэтому от проверки косового произведения нам никуда не деться. Для достаточного условия нужно вычислить еще и скалярное произведение тех же векторов. Если оно меньше нуля, то точка не принадлежит лучу, если же оно не отрицательно, то точка лежит на луче. Почему так? Давайте посмотрим на рисунок.
Итак, для того чтобы точка M(x, y) лежала на луче с начальной точкой P1(x1, y1), где P2(x2, y2) лежит на луче необходимо и достаточно выполнения двух условий:
1. [P1P2, P1M] = 0 – косое произведение (точка лежит на прямой)
2. (P1P2, P1M) ≥ 0 – скалярное произведение (точка лежит на луче)
Задача №3
Определить принадлежит ли точка отрезку.
Решение
Пусть точки P1(x1, y1), P2(x2, y2) концы заданного отрезка. Опять-таки необходимым условием принадлежности точки отрезку является ее принадлежность прямой проходящей через P1, P2. Далее нам нужно определить лежит ли точка между точками P1 и P2, для этого нам на помощь приходит скалярное произведение векторов только на этот раз других: (MP1, MP2). Если оно меньше либо равно нуля, то точка лежит на отрезке, иначе вне отрезка. Почему так? Посмотрим на рисунок.
Итак, для того чтобы точка M(x, y) лежала на отрезке с концами P1(x1, y1), P2(x2, y2) необходимо и достаточно выполнения условий:
1. [P1P2, P1M] = 0 – косое произведение (точка лежит на прямой)
2. (MP1,MP2) ≤ 0 – скалярное произведение (точка лежит между P1 и P2)
Задача №4
Взаимное расположение двух точек относительно прямой.
Решение
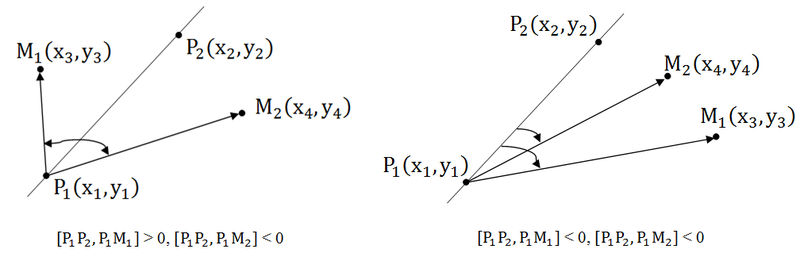
В этой задаче необходимо определить по одну или по разные стороны относительно прямой находятся две точки.
Если точки находятся по разные стороны относительно прямой, то косые произведения имеют разные знаки, а значит их произведение отрицательно. Если же точки лежат по одну сторону относительно прямой, то знаки косых произведений совпадают, значит, их произведение положительно.
Итак:
1. [P1P2, P1M1] * [P1P2, P1M2] < 0 – точки лежат по разные стороны.
2. [P1P2, P1M1] * [P1P2, P1M2] > 0 – точки лежат по одну сторону.
3. [P1P2, P1M1] * [P1P2, P1M2] = 0 – одна (или две) из точек лежит на прямой.
Кстати, задача об определении наличия точки пересечения у прямой и отрезка решается точно также. Точнее, это и есть эта же задача: отрезок и прямая пересекаются, когда концы отрезка находятся по разные стороны относительно прямой или когда концы отрезка лежат на прямой, то есть необходимо потребовать [P1P2, P1M1] * [P1P2, P1M2] ≤ 0.
Задача №5
Определить пересекаются ли две прямые.
Решение
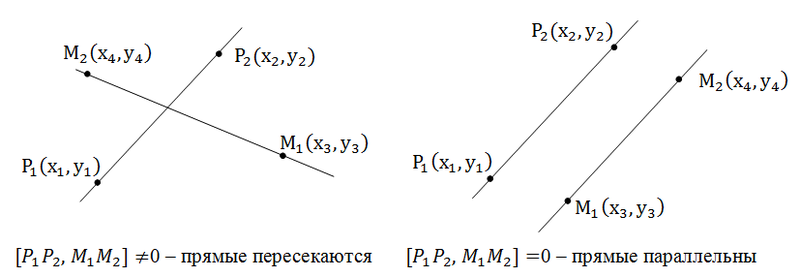
Будем считать, что прямые не совпадают. Понятно, что прямые не пересекаются, только если они параллельны. Поэтому, найдя условие параллельности, мы можем, определить пересекаются ли прямые.
Допустим прямые заданы своими уравнениями a1x + b1y + c1 = 0 и a2x + b2y + c2 = 0. Тогда условие параллельности прямых заключается в том, что a1b2 — a2b1 = 0.
Если же прямые заданы точками P1(x1, y1), P2(x2, y2), M1(x3, y3), M2(x4, y4), то условие их параллельности заключается в проверки косого произведения векторов P1P2 и M1M2: если оно равно нулю, то прямые параллельны.
В общем, то когда прямые заданы своими уравнениями мы тоже проверяем косое произведение векторов (-b1, a1), (-b2, a2) которые называются направляющими векторами.
Задача №6
Определить пересекаются ли два отрезка.
Решение
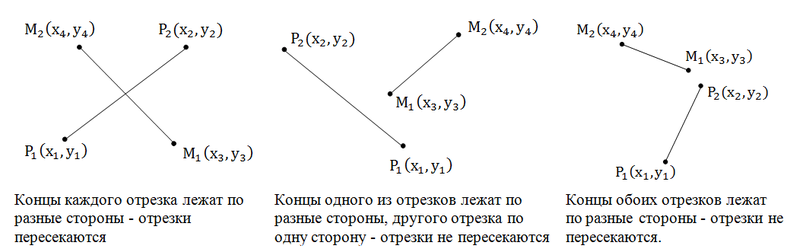
Вот эта задача мне, действительно, нравится. Отрезки пересекаются тогда, когда, концы каждого отрезка лежат по разные стороны от другого отрезка. Посмотрим на рисунок:
Итак, нам нужно проверить, чтобы концы каждого из отрезков лежали по разные стороны относительного концов другого отрезка. Пользуемся косым произведением векторов. Посмотрите на первый рисунок: [P1P2, P1M2] > 0, [P1P2, P1M1] < 0 => [P1P2, P1M2] * [P1P2, P1M1] < 0. Аналогично
[M1M2, M1P1] * [M1M2, M1P2] < 0. Вы наверно думаете, почему не меньше либо равно. А потому, что возможен следующий случай, при котором векторное произведение как раз и равно нулю, но отрезки не пересекаются:
Поэтому нам необходимо сделать еще одну проверку, а именно: принадлежит ли хотя бы один конец каждого отрезка другому (принадлежность точки отрезку). Эту задачу мы уже решали.
Итак, для того чтобы отрезки имели общие точки необходимо и достаточно:
1. Концы отрезков лежат по разные стороны относительно другого отрезка.
2. Хотя бы один из концов одного отрезка принадлежит другому отрезку.
Задача №7
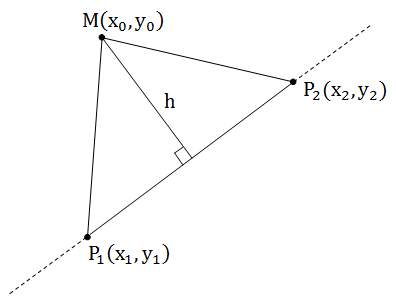
Расстояние от точки до прямой.
Решение
Пусть прямая задана двумя точками P1(x1, y1) и P2(x2, y2).
В предыдущей статье мы говорили о том, что геометрически косое произведение — это ориентированная площадь параллелограмма, поэтому SP1P2M = 0,5*[P1P2, P1M]. С другой стороны каждому школьнику известна формула для нахождения площади треугольника: половина основание на высоту.
SP1P2M = 0,5*h*P1P2.
Приравнивая эти площади, находим
По модулю взяли потому, что первая площадь ориентированная.
Если же прямая задана уравнением ax + by + c = 0, то уравнение прямой проходящей через точку M перпендикулярной заданной прямой есть: a(y — y0) – b(x — x0) = 0. Теперь спокойно можно решить систему из полученных уравнений, найти их точку пересечения и вычислить расстояние от исходной точки до найденной: оно будет ровно ρ = (ax0 + by0 + c)/√(a2 + b2).
Задача №8
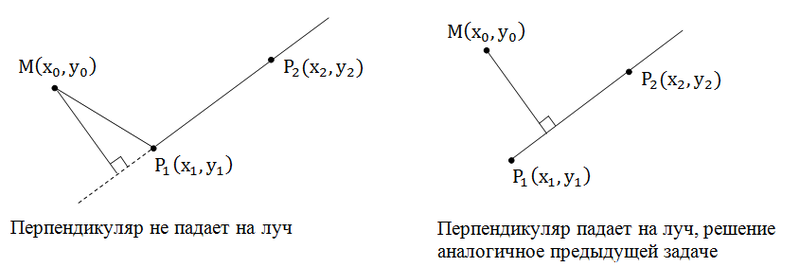
Расстояние от точки до луча.
Решение
Эта задача отличается от предыдущей тем, что в этом случае может получиться, так что перпендикуляр из точки не падает на луч, а падает на его продолжение.
В случае, когда перпендикуляр не падает на луч необходимо найти расстояние от точки до начала луча – это и будет ответом на задачу.
Как же определить падает ли перпендикуляр на луч или нет? Если перпендикуляр не падает на луч, то угол MP1P2 – тупой иначе острый (прямой). Поэтому по знаку скалярного произведения векторов мы можем определить попадает ли перпендикуляр на луч или нет:
1. (P1M, P1P2) < 0 перпендикуляр не попадает на луч
2. (P1M, P1P2) ≥ 0 перпендикуляр попадает на луч
Задача №9
Расстояние от точки до отрезка.
Решение
Рассуждаем аналогично предыдущей задаче. Если перпендикуляр не падает на отрезок, то ответом будет минимальное из расстояний от данной точки до концов отрезка.
Чтобы определить попадает ли перпендикуляр на отрезок нужно по аналогии с предыдущей задачей использовать скалярное произведение векторов. Если перпендикуляр не падает на отрезок, то либо угол MP1P2 либо угол MP2P1 будут тупыми. Поэтому по знаку скалярных произведений мы можем определить попадает ли перпендикуляр на отрезок или нет:
Если (P1M, P1P2) < 0 или (P2M, P2P1) < 0 то перпендикуляр не падает на отрезок.
Задача №10
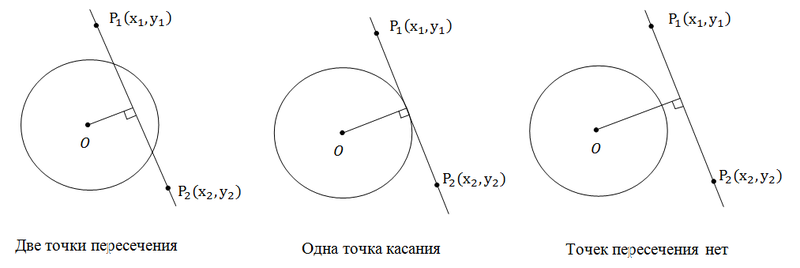
Определить количество точек прямой и окружности.
Решение
Прямая и окружность может иметь нуль, одну или две точки пересечения. Давайте посмотрим на рисунки:
Здесь из рисунков и так все понятно. Мы имеем две точки пересечения, если расстояние от центра окружности до прямой меньше радиуса окружности. Одну точку касания, если расстояние от центра до прямой равно радиусу. И наконец, ни одной точки пересечения, если расстояние от центра окружности до прямой больше радиуса окружности. Поскольку задача нахождения расстояние от точки до прямой была уже нами решена, то и эта задача тоже решена.
Задача №11
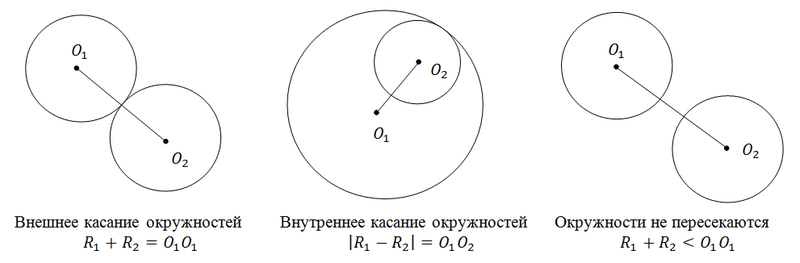
Взаимное расположение двух окружностей.
Решение
Возможные случаи расположения окружностей: пересекаются, касаются, не пересекаются.
Рассмотрим случай, когда окружности пересекаются, и найдем площадь их пересечения. Эту задачу я очень люблю, так как потратил на ее решение изрядное количество времени (было это давно — на первом курсе).
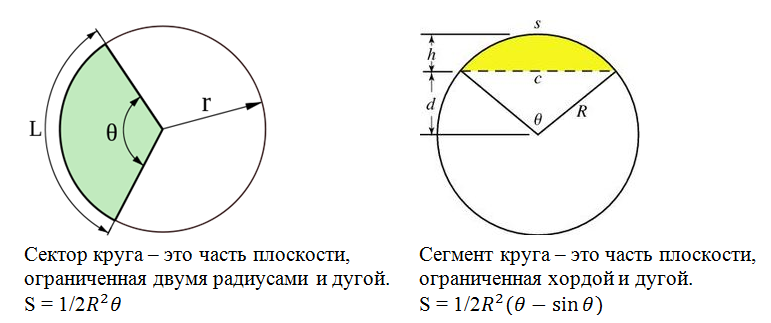
Вспомним теперь, что такое сектор и сегмент.
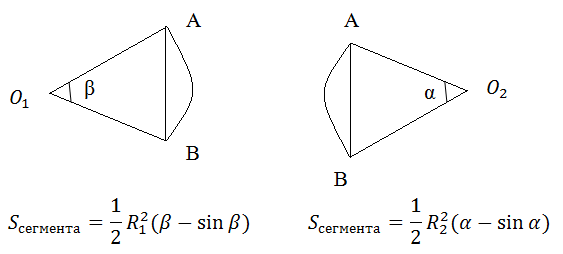
Пересечение кругов состоит из двух сегментов O1AB и O2AB.
Казалось бы необходимо сложить площади этих сегментов и все. Однако, все не так просто. Необходимо еще определить всегда ли эти формулы верны. Оказывается, нет!
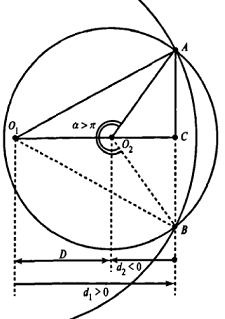
Рассмотрим случай, когда центр второго круга O2 совпадает с точкой C. В этом случае d2 = 0 и за значение α примем α = π. В этом случае имеем полукруг с площадью 1/2 πR22.
Теперь рассмотрим случай, когда центр второго круга O2 находится между точками O1 и C. В этом случае получим отрицательное значение величины d2. Использование отрицательного значения d2 приводит к отрицательному значению α. В этом случае необходимо для правильного ответа прибавить к α 2π.
Заключение
Ну вот и все. Мы рассмотрели не все, но наиболее часто встречаемые задачи вычислительной геометрии касающиеся взаимного расположения объектов.
Надеюсь, Вам понравилось.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 |
#include <iostream> #include <vector> #include <limits> #include <string> #include <algorithm> using namespace std; double dist_point_point(double x1, double y1, double x2, double y2) { return sqrt((x1-x2)*(x1-x2)+(y1-y2)*(y1-y2)); } double dist_point_line(double x, double y, double x1, double y1, double x2, double y2) { double det = abs((y1 - y2) * (x1 - x) - (x1 - x2) * (y1 - y)); x1 -= x2; y1 -= y2; det /= sqrt(x1 * x1 + y1 * y1); return det; } bool comp(double x, double y) { return (abs(x - y) <= 1e-9); } bool inRay(double x, double y, double x1, double y1, double x2, double y2) { // x, y must be in line with ray double kx1 = x2 - x1; double ky1 = y2 - y1; double d = dist_point_point(x1, y1, x2, y2); kx1 /= d; ky1 /= d; double kx2 = x - x1; double ky2 = y - y1; double d2 = dist_point_point(x1, y1, x, y); kx2 /= d2; ky2 /= d2; return (comp(kx1, kx2) && comp(ky1, ky2)); } double dist_point_ray(double x, double y, double x1, double y1, double x2, double y2) { double dpl = dist_point_line(x, y, x1, y1, x2, y2); double A = y2 - y1; double B = x1 - x2; double cf = sqrt(A*A + B*B); A /= cf; // Normalize B /= cf; // Normalize double xp1 = x + A * dpl; double yp1 = y + B * dpl; double xp2 = x - A * dpl; double yp2 = y - B * dpl; double dpl1 = dist_point_line(xp1, yp1, x1, y1, x2, y2); double dpl2 = dist_point_line(xp2, yp2, x1, y1, x2, y2); if (dpl2 < dpl1) { swap(xp1, xp2); swap(yp1, yp2); } if (inRay(xp1, yp1, x1, y1, x2, y2)) return dpl; else return min(dist_point_point(x, y, x1, y1), dist_point_point(x, y, x2, y2)); } int main(){ freopen("input.txt", "rt", stdin); freopen("output.txt", "wt", stdout); double x, y, x1, y1, x2, y2; scanf("%lf%lf%lf%lf%lf%lf", &x, &y, &x1, &y1, &x2, &y2); printf("%.15lf", dist_point_ray(x, y, x1, y1, x2, y2)); return 0; } |
Данный круг с данным радиусом имеет свой центр в определенной позиции в координатной плоскости. В координатной плоскости задается другая точка. Задача — найти кратчайшее расстояние между точкой и окружностью.
Ниже приведена реализация вышеуказанного подхода:
// C ++ программа для поиска
// Наименьшее расстояние
// между точкой и
// круг
#include
using namespace std;
// Функция для поиска кратчайшего расстояния
void dist( double x1, double y1, double x2, double y2, double r)
cout «The shortest distance «
«between a point and a circle is «
sqrt (( pow ((x2 — x1), 2))
double x1 = 4, y1 = 6,
x2 = 35, y2 = 42, r = 5;
dist(x1, y1, x2, y2, r);
// Java-программа для поиска
// Наименьшее расстояние
// между точкой и
// круг
// Функция для поиска кратчайшего расстояния
static void dist( double x1, double y1, double x2,
double y2, double r)
System.out.println( «The shortest distance «
+ «between a point and a circle is «
+ (Math.sqrt((Math.pow((x2 — x1), 2 ))
+ (Math.pow((y2 — y1), 2 )))
public static void main(String[] args)
double x1 = 4 , y1 = 6 ,
x2 = 35 , y2 = 42 , r = 5 ;
dist(x1, y1, x2, y2, r);
/ * Этот код предоставлен PrinciRaj1992 * /
# Python программа для поиска
# Наименьшее расстояние
# между точкой и
# круг
# Функция поиска кратчайшего расстояния
def dist(x1, y1, x2, y2, r):
print ( «The shortest distance between a point and a circle is «
,((((x2 — x1) * * 2 ) + ((y2 — y1) * * 2 )) * * ( 1 / 2 )) — r);
dist(x1, y1, x2, y2, r);
# Этот код предоставлен 29AjayKumar
// C # программа для поиска кратчайшего расстояния
// между точкой и окружностью
// Функция для поиска кратчайшего расстояния
static void dist( double x1, double y1, double x2,
double y2, double r)
Console.WriteLine( «The shortest distance «
+ «between a point and a circle is «
+ (Math.Sqrt((Math.Pow((x2 — x1), 2))
+ (Math.Pow((y2 — y1), 2)))
public static void Main(String[] args)
double x1 = 4, y1 = 6,
x2 = 35, y2 = 42, r = 5;
dist(x1, y1, x2, y2, r);
/ * Этот код предоставлен PrinciRaj1992 * /
// PHP программа для поиска
// Наименьшее расстояние
// между точкой и
// круг
// Функция для поиска кратчайшего расстояния
function dist( $x1 , $y1 , $x2 , $y2 , $r )
echo «The shortest distance between a point and a circle is «
Всё про окружность и круг
Окружность — это геометрическое место точек плоскости, равноудаленных от некоторой заданной точки (центра окружности). Расстояние между любой точкой окружности и ее центром называется радиусом окружности (радиус обозначают буквой R).
Значит, окружность — это линия на плоскости, каждая точка которой расположена на одинаковом расстоянии от центра окружности.
Кругом называется часть плоскости, ограниченная окружностью и включающая ее центр.
Отрезок, соединяющий две точки окружности, называется хордой. Хорда, проходящая через центр окружности, представляет собой диаметр. Диаметр окружности равен ее удвоенному радиусу: D = 2R.
Точка пересечения двух хорд делит каждую хорду на отрезки, произведение которых одинаково: a1a2 = b1b2
Касательная к окружности всегда перпендикулярна радиусу, проведенному в точку касания.
Отрезки касательных к окружности, проведенные из одной точки, равны: AB = AC, центр окружности лежит на биссектрисе угла BAC.
Квадрат касательной равен произведению секущей на ее внешнюю часть
Центральный угол — это угол, вершина которого совпадает с центром окружности.
Дугой называется часть окружности, заключенная между двумя точками.
Мерой дуги (в градусах или радианах) является центральный угол, опирающийся на данную дугу.
Вписанный угол это угол, вершина которого лежит на окружности, а cтороны угла пересекают ее.
Вписанный угол равен половине центрального, если оба угла опираются на одну и ту же дугу окружности.
Внутренние углы, опирающиеся на одну и ту же дугу, равны.
Сектором круга называется геометрическая фигура, ограниченная двумя радиусами и дугой, на которую опираются данные радиусы.
Периметр сектора: P = s + 2R.
Площадь сектора: S = Rs/2 = ПR 2 а/360°.
Сегментом круга называется геометрическая фигура, ограниченная хордой и стягиваемой ею дугой.
Вычислительная геометрия, или как я стал заниматься олимпиадным программированием. Часть 2
Вступление
Это вторая часть моей статьи посвящена вычислительной геометрии. Думаю, эта статья будет интереснее предыдущей, поскольку задачки будут чуть сложнее.
Начнем с взаимного расположения точки относительно прямой, луча и отрезка.
Задача №1
Определить взаимное расположении точки и прямой: лежит выше прямой, на прямой, под прямой.
Решение
Понятно, что если прямая задана своим уравнением ax + by + c = 0, то тут и решать нечего. Достаточно подставить координаты точки в уравнение прямой и проверить чему оно равно. Если больше нуля, то точка находится в верхней полуплоскости, если равна нулю, то точка находится на прямой и если меньше нуля, то точка находится в нижней полуплоскости. Интереснее случай, когда прямая задана, задана координатами двух точек назовем их P1(x1, y1), P2(x2, y2). В этом случае можно спокойно найти коэффициенты a, b и c и применить предыдущее рассуждение. Но надо сначала подумать, оно нам надо? Конечно, нет! Как я говорил косое произведения — это просто жемчужина вычислительной геометрии. Давайте применим его. Известно, что косое произведение двух векторов положительно, если поворот от первого вектора ко второму идет против часовой стрелки, равно нулю, если векторы коллинеарны и отрицательно, если поворот идет по часовой стрелки. Поэтому нам достаточно посчитать косое произведение векторов P1P2 и P1M и по его знаку сделать вывод.
Задача №2
Определить принадлежит ли точка лучу.
Решение
Давайте вспомним, что такое луч: луч — это прямая, ограниченная точкой с одной стороны, а с другой стороны бесконечная. То есть луч задается некоторой начальной точкой и любой точкой лежащей на нем. Пусть точка P1(x1, y1) — начало луча, а P2(x2, y2) — любая точка принадлежащая лучу. Понятно, что если точка принадлежит лучу, то она принадлежит и прямой проходящей через эти точки, но не наоборот. Поэтому принадлежность прямой является необходимым, но не достаточным условием для принадлежности лучу. Поэтому от проверки косового произведения нам никуда не деться. Для достаточного условия нужно вычислить еще и скалярное произведение тех же векторов. Если оно меньше нуля, то точка не принадлежит лучу, если же оно не отрицательно, то точка лежит на луче. Почему так? Давайте посмотрим на рисунок.
Итак, для того чтобы точка M(x, y) лежала на луче с начальной точкой P1(x1, y1), где P2(x2, y2) лежит на луче необходимо и достаточно выполнения двух условий:
1. [P1P2, P1M] = 0 – косое произведение (точка лежит на прямой)
2. (P1P2, P1M) ≥ 0 – скалярное произведение (точка лежит на луче)
Задача №3
Определить принадлежит ли точка отрезку.
Решение
Пусть точки P1(x1, y1), P2(x2, y2) концы заданного отрезка. Опять-таки необходимым условием принадлежности точки отрезку является ее принадлежность прямой проходящей через P1, P2. Далее нам нужно определить лежит ли точка между точками P1 и P2, для этого нам на помощь приходит скалярное произведение векторов только на этот раз других: (MP1, MP2). Если оно меньше либо равно нуля, то точка лежит на отрезке, иначе вне отрезка. Почему так? Посмотрим на рисунок.
Итак, для того чтобы точка M(x, y) лежала на отрезке с концами P1(x1, y1), P2(x2, y2) необходимо и достаточно выполнения условий:
1. [P1P2, P1M] = 0 – косое произведение (точка лежит на прямой)
2. (MP1,MP2) ≤ 0 – скалярное произведение (точка лежит между P1 и P2)
Задача №4
Взаимное расположение двух точек относительно прямой.
Решение
В этой задаче необходимо определить по одну или по разные стороны относительно прямой находятся две точки.
Если точки находятся по разные стороны относительно прямой, то косые произведения имеют разные знаки, а значит их произведение отрицательно. Если же точки лежат по одну сторону относительно прямой, то знаки косых произведений совпадают, значит, их произведение положительно.
Итак:
1. [P1P2, P1M1] * [P1P2, P1M2] 0 – точки лежат по одну сторону.
3. [P1P2, P1M1] * [P1P2, P1M2] = 0 – одна (или две) из точек лежит на прямой.
Кстати, задача об определении наличия точки пересечения у прямой и отрезка решается точно также. Точнее, это и есть эта же задача: отрезок и прямая пересекаются, когда концы отрезка находятся по разные стороны относительно прямой или когда концы отрезка лежат на прямой, то есть необходимо потребовать [P1P2, P1M1] * [P1P2, P1M2] ≤ 0.
Задача №5
Определить пересекаются ли две прямые.
Решение
Будем считать, что прямые не совпадают. Понятно, что прямые не пересекаются, только если они параллельны. Поэтому, найдя условие параллельности, мы можем, определить пересекаются ли прямые.
Допустим прямые заданы своими уравнениями a1x + b1y + c1 = 0 и a2x + b2y + c2 = 0. Тогда условие параллельности прямых заключается в том, что a1b2 — a2b1 = 0.
Если же прямые заданы точками P1(x1, y1), P2(x2, y2), M1(x3, y3), M2(x4, y4), то условие их параллельности заключается в проверки косого произведения векторов P1P2 и M1M2: если оно равно нулю, то прямые параллельны.
В общем, то когда прямые заданы своими уравнениями мы тоже проверяем косое произведение векторов (-b1, a1), (-b2, a2) которые называются направляющими векторами.
Задача №6
Определить пересекаются ли два отрезка.
Решение
Вот эта задача мне, действительно, нравится. Отрезки пересекаются тогда, когда, концы каждого отрезка лежат по разные стороны от другого отрезка. Посмотрим на рисунок:
Итак, нам нужно проверить, чтобы концы каждого из отрезков лежали по разные стороны относительного концов другого отрезка. Пользуемся косым произведением векторов. Посмотрите на первый рисунок: [P1P2, P1M2] > 0, [P1P2, P1M1] [P1P2, P1M2] * [P1P2, P1M1] 2 + b 2 ).
Задача №8
Расстояние от точки до луча.
Решение
Эта задача отличается от предыдущей тем, что в этом случае может получиться, так что перпендикуляр из точки не падает на луч, а падает на его продолжение.
В случае, когда перпендикуляр не падает на луч необходимо найти расстояние от точки до начала луча – это и будет ответом на задачу.
Как же определить падает ли перпендикуляр на луч или нет? Если перпендикуляр не падает на луч, то угол MP1P2 – тупой иначе острый (прямой). Поэтому по знаку скалярного произведения векторов мы можем определить попадает ли перпендикуляр на луч или нет:
1. (P1M, P1P2) 2 .
Теперь рассмотрим случай, когда центр второго круга O2 находится между точками O1 и C. В этом случае получим отрицательное значение величины d2. Использование отрицательного значения d2 приводит к отрицательному значению α. В этом случае необходимо для правильного ответа прибавить к α 2π.
Заключение
Ну вот и все. Мы рассмотрели не все, но наиболее часто встречаемые задачи вычислительной геометрии касающиеся взаимного расположения объектов.
http://www.stranamam.ru/post/8974384/
http://habr.com/ru/post/148325/
Содержание:
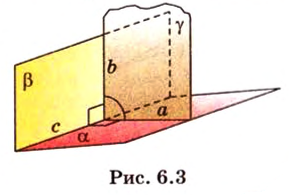
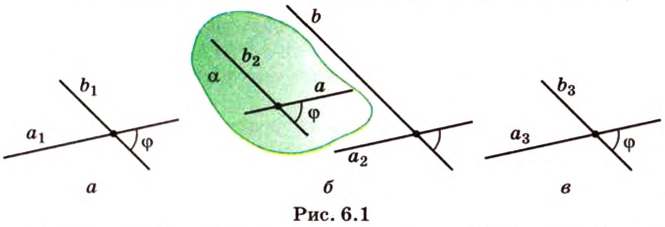
В планиметрии угол — это геометрическая фигура, образованная двумя лучами, которые выходят из одной точки — вершины угла (лучи — стороны угла). Такое определение понятия угла переносится и в стереометрию. Углы в пространстве рассматриваются между двумя прямыми, прямой и плоскостью, двумя плоскостями. Опишем и определим каждый из этих случаев.
Угол между двумя прямыми в пространстве
Две прямые, лежащие в одной плоскости, при пересечении образуют смежные и вертикальные углы. В модуле 1 мы повторили все свойства таких углов (вертикальные углы равны, а смежные — дополняют друг друга до 180°). В пространстве (аналогично планиметрии) также сохраняются все названия и понятия об углах и их величинах. Меньший из углов, образованных двумя пересекающимися прямыми, называют углом между прямыми. Угол между перпендикулярными прямыми равен 90°. Считают, что параллельные прямые также образуют угол, равный 0°. В стереометрии рассматривают угол между скрещивающимися прямыми. Пусть даны скрещивающиеся прямые
Углом между скрещивающимися прямыми называется угол между прямыми, которые пересекаются и соответственно параллельны скрещивающимся. 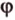
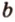
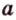
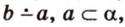
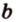
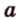
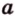
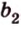
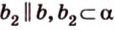
Итак,
Если 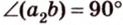
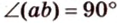
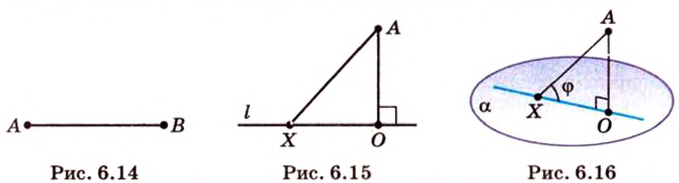
Угол между прямой и плоскостью в пространстве
Об угле наклона прямой к плоскости говорят в том случае, когда прямая пересекает эту плоскость. Чтобы построить, например, угол между прямой 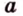
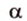
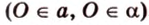
- выбирают точку
прямой
;
- проводят из точки
перпендикуляр к плоскости
;
- проводят через точки плоскости
и
прямую
.
Прямую 
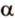
Углом между прямой и плоскостью называется угол между этой прямой и ее проекцией на плоскость. Если прямая 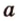
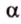
Угол между прямой 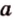
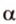
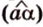
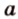
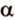
Угол между двумя плоскостями, пространства
Прямая на плоскости разбивает ее на две полуплоскости. Две полуплоскости могут иметь общую прямую и не образовывать одну плоскость. В этом случае они образуют фигуру, которую называют двугранным углом.
Двугранным углом называется фигура, образованная двумя полуплоскостями вместе с общей прямой, их ограничивающей. Эту прямую называют ребром двугранного угла.
Если двугранный угол пересечь плоскостью, перпендикулярной его ребру, то лучи, по которым она пересекает заданные
полуплоскости, образуют линейный угол, например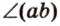
Пересекающиеся плоскости образуют четыре угла. Чтобы определить угол между двумя плоскостями, проводят плоскость, перпендикулярную прямой их пересечения. Она пересекает данные плоскости по двум прямым. Угол между этими прямыми называется углом между данными плоскостями. Т.е. угол между двумя пересекающимися плоскостями — это угол между двумя прямыми, которые принадлежат этим плоскостям и перпендикулярны прямой их пересечения.
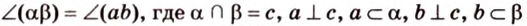
Если линейный угол — 90°, то плоскости перпендикулярны. Если плоскости параллельны, то угол между ними равен 0°.
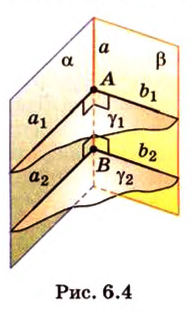
Теорема 1
Угол между плоскостями не зависит от места построения линейного угла.
Доказательство:
Выберем точки 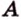
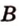
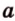
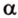
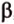
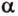
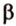
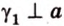
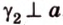
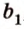
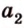
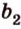
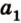
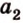
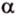
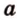
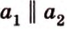
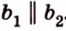
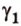
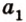
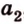
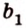
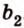
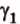
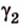
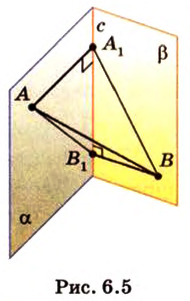
Пример №1
Концы отрезка длиной 24 см принадлежат двум перпендикулярным плоскостям. Расстояния от концов отрезка до линии пересечения данных плоскостей равны 12 см и 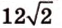
Дано: 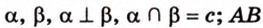

Найти: углы, образованные отрезком 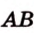
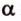
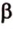
Решение:
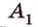
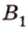
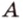
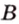
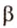
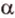
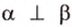
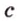
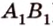
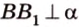
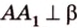
Итак, 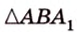
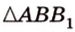
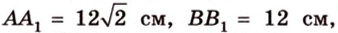
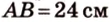
Из 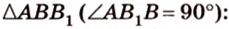
Из 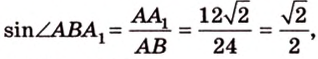
Ответ. 30°; 45°.
Почему именно так?
В этой задаче важно построить проекции концов отрезка на другую, перпендикулярную ей, плоскость. При этом следует помнить, что они должны лежать на прямой пересечения данных перпендикулярных плоскостей, согласно свойствам перпендикулярных плоскостей. Далее, рассматривая прямоугольные треугольники, нужно правильно использовать определение синуса угла как отношения противолежащего катета к гипотенузе и таблицу значений:
Расстояния в пространстве
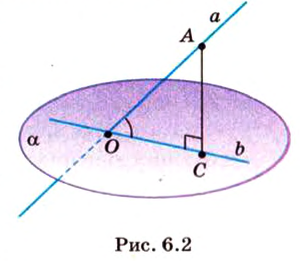
Одним из ключевых понятий геометрии является длина отрезка. Через него вводится много других понятий, связанных с понятием расстояния. Как известно, расстоянием между двумя точками 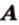
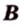
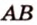
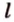
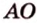
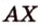
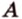
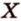
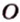
Рассмотрим плоскость 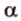
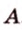
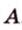
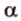
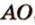
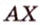
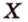
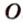
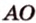
Итак, расстояние от точки до плоскости равно длине перпендикуляра, проведенного из этой точки к плоскости.
Если точка принадлежит плоскости, то в этом случае расстояние от нее до плоскости равно нулю.
Расстояние от точки 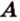
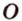
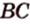
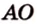
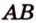

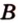
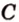
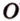
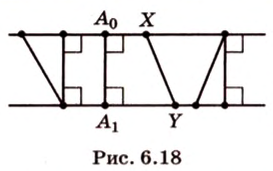
Расстояние между двумя параллельными прямыми равно длине общего перпендикуляра этих прямых (рис. 6.18). Это вытекает из того, что все такие перпендикуляры 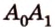
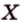
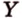
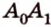
Теорема 2 (о расстоянии между параллельными прямой и плоскостью)
Расстояние между параллельными прямой и плоскостью равно длине общего перпендикуляра, проведенного из произвольной точки прямой к плоскости.
Данная теорема доказывается рассуждениями, аналогичными приведенным выше, о расстоянии между параллельными прямыми.
Теорема 3 (о расстоянии между параллельными плоскостями)
Расстояние между параллельными плоскостями равно длине общего перпендикуляра, проведенного из произвольной точки одной плоскости ко второй.
Доказательство:
Пусть имеем две параллельные плоскости 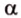
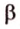
и второй, то перпендикуляр 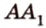
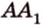
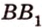
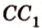
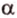
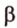
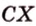
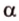
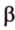
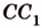
А это вытекает из того, что перпендикуляр 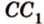
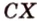
Понятие расстояния между точками широко применяется в разнообразных сферах жизни человека — от науки до быта и досуга. Используется оно в тех случаях, когда размерами реальных объектов, расстояние между которыми вычисляется, в данных условиях можно пренебречь. Так мы говорим о расстоянии между звездами, планетами, передатчиками и принима-телями информации, населенными пунктами, ядрами атома и электронами на его орбите и т.п.
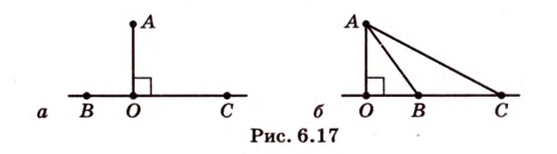
Расстояние между скрещивающимися прямыми
Сначала рассмотрим определение перпендикуляра, проведенного к двум скрещивающимся прямым, и докажем его существование и единственность.
Общим перпендикуляром к двум скрещивающимся прямым называется отрезок с концами на этих прямых, перпендикулярный каждой из них.
Теорема 4
Две скрещивающиеся прямые имеют общий перпендикуляр, и притом только один. Он является общим перпендикуляром к параллельным плоскостям, проходящим через эти прямые.
Доказательство:
Действительно, пусть 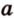
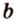
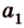
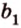
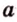
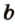
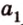
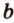
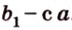
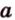
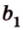
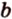
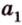
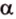
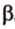
Плоскости 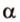
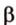
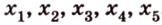
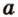
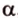
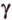
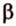
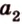
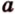
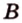
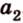
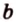
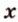
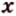
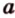
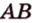
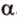
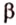
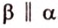
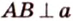
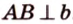
Отрезок 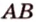
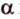
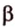
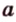
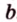
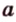
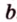
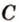
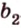
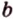

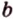
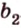
Поскольку она перпендикулярна прямым 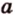
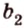

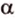




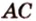
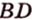
Расстоянием между скрещивающимися прямыми называется длина их общего перпендикуляра.
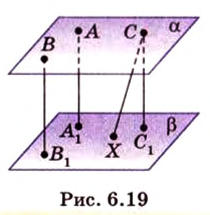
Пример №2
Отрезок 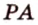
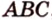
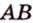
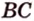
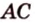
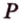
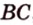
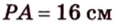
Решение:
Пусть 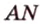
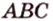
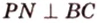
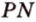
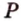
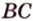
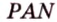
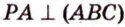
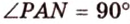
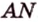
Из формулы для площади треугольника 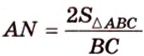
Необходимую площадь определим по формуле Герона:
Тогда 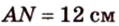
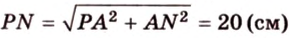
Ответ. 20 см.
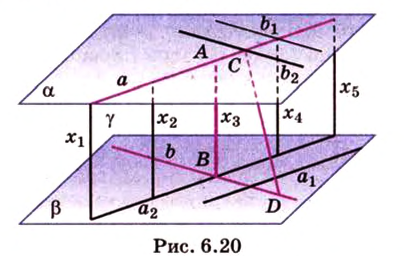
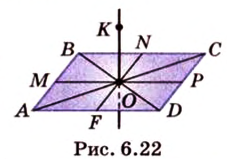
Пример №3
Прямая 
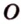
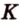
Доказательство:
Пусть 
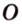
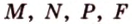
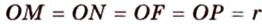
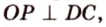
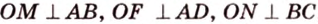
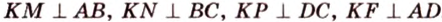
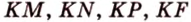
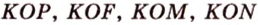
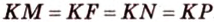
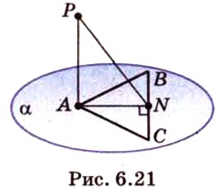
Пример №4
Точка 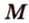
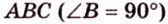
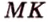
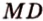
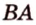
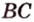
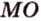
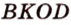
Доказательство:
Поскольку отрезки 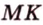
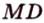
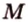
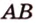
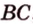
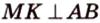
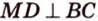
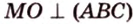
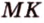
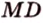
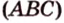
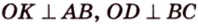
- Подобие треугольников
- Решение прямоугольных треугольников
- Параллелограмм
- Теорема синусов и теорема косинусов
- Квадрат и его свойства
- Трапеция и ее свойства
- Площадь трапеции
- Центральные и вписанные углы
Содержание:
- § 1 Числовой луч
- § 2 Сложение и вычитание с помощью числового луча
- § 3 Координаты на луче
- § 4 Краткие итоги урока
§ 1 Числовой луч
В этом уроке познакомимся с числовым лучом, научимся определять координаты на числовом луче и находить расстояние между точками числового луча.
Для начала вспомним, что такое луч?
Лучом называют часть прямой, у которой есть начало, но нет конца.
Начертим луч, который располагается слева направо.
Выберем единичный отрезок е и отложим его последовательно от начала луча несколько раз.
Отметим начало луча числом 0, а последующие отмеченные точки луча соответствующими числами 1, 2, 3, 4, 5 и т.д.
Таким образом, мы нанесли на луч шкалу.
Шкала – это деления и числа, сопоставленные им по некоторому закону. Каждое деление полученной шкалы равно единичному отрезку е.
Получившийся луч, который направлен слева направо и имеет шкалу разметки, а начало луча совпадает с числом 0, называют числовым лучом.
На числовом луче можно отметить любое число: как натуральное, так и дробное.
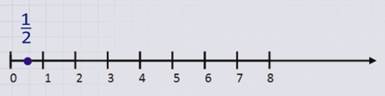
Отметим на нашем числовом луче числа ½, 2 ¼ .
Число ½ больше 0, но меньше 1 и эта дробь показывает, что отрезок на числовом луче от 0 до 1, разделили на две части и взяли одну.
Отметим число ½.
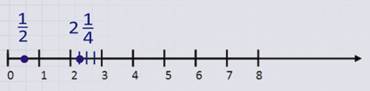
Число 2 ¼ состоит из целой части – числа 2 и дробной части ¼.
Целая часть числа 2 ¼ показывает, что 2 ¼ больше 2, но меньше 3.
Дробная часть ¼ показывает, что отрезок на числовом луче от 2 до 3 разделили на 4 части и взяли одну.
Отметим число 2 ¼ на числовом луче.
При помощи числового луча сравним данные числа ½ и 2 ¼.
Из рисунка видно, что меньшее число ½ располагается ближе к началу числового луча – числу 0, чем большее число 2 ¼.
Значит, можем сделать вывод: из двух чисел меньше то, которое расположено на числовом луче левее, а больше то, которое расположено правее.
Число ½ расположено левее числа 2 ¼.
Значит, ½ < 2 ¼ .
§ 2 Сложение и вычитание с помощью числового луча
На числовом луче можно также прибавлять и вычитать числа.
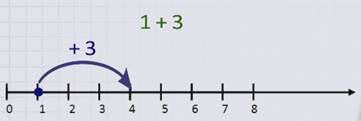
Например: при помощи числового луча выполним сложение чисел 1 и 3.
Для этого поставим точку на числовом луче на деление с числом 1.
Отсчитаем вправо от 1 количество делений, равное второму слагаемому 3.
Покажем это стрелкой.
Число, соответствующее полученному делению, и будет суммой чисел 1 и 3, а именно 4.
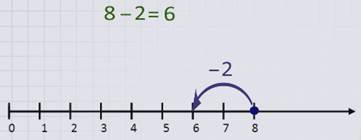
Выполним вычитание чисел 8 и 2 при помощи числового луча.
Для этого на делении с числом 8 поставим точку.
Отсчитаем от точки влево два деления, так как вычитаемое равно 2.
Покажем это дугой. Число, соответствующее полученному делению, и будет разницей чисел 8 и 2, а именно 6.
§ 3 Координаты на луче
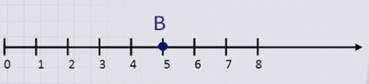
Начертим еще один числовой луч.
Отметим на нем точку В, которая удалена от начала числового луча на 5 единиц или 5 единичных отрезка.
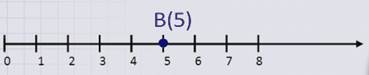
Число, показывающее расстояние от точки В на луче до начала луча, выраженное в выбранных единицах, называется координатой точки В.
Из рисунка видно, что точка В имеет координату 5.
Пишут так: В(5).
При движении точки по лучу направо ее координата увеличивается, а при движении налево – уменьшается.
Поскольку точки на числовом луче имеют координаты, то числовой луч также называют координатным лучом.
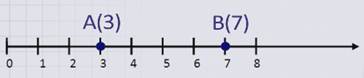
Начертим координатный луч и отметим на нем две точки: точку А с координатой 3 и точку В с координатой 7.
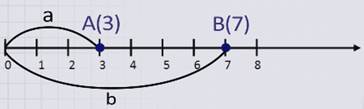
Найдем расстояние между точками А и В.
Расстояние а от начала координатного луча до точки А равно 3.
Расстояние b от начала координатного луча до точки В равно 7.
Расстояние АВ между точками А и В неизвестно.
Помним, что на числовом или координатном луче можно складывать и вычитать числа, а также чем правее точка на координатном луче от начала луча, тем ее координата больше.
Можем сделать вывод: чтобы найти расстояние между двумя точками координатного луча, можно из большей координаты вычесть меньшую.
АВ = b – a.
Координата точки А равна 3, а координата точки В равна 7. Значит, расстояние между точками АВ = b – a = 7 – 3 = 4.
§ 4 Краткие итоги урока
Подведем итоги урока:
1. Числовой луч – это луч, который направлен слева направо и имеет шкалу разметки, а начало луча совпадает с числом 0.
2. Из двух чисел меньше то, которое расположено на числовом луче левее, а больше то, которое расположено правее.
3. Координата – это число, показывающее расстояние от точки на луче до начала луча, выраженное в выбранных единицах.
4. Чтобы найти расстояние между двумя точками координатного луча, можно из большей координаты вычесть меньшую. АВ = b – a.
Список использованной литературы:
- Петерсон Л.Г. Математика. 4 класс. Часть 2 / Л.Г. Петерсон. – М.: Ювента, 2014. – 96 с.: ил.
- Математика. 4 класс. Методические рекомендации к учебнику математики «Учусь учиться» для 4 класса / Л.Г. Петерсон. – М.: Ювента, 2014. – 280 с.: ил.
- Зак С.М. Все задания к учебнику математики для 4 класса Л.Г. Петерсон и комплекту самостоятельных и контрольных работ. ФГОС. – М.: ЮНВЕС, 2014.
- CD-ROM. Математика. 4 класс. Сценарии уроков к учебнику к 2 части Петерсон Л.Г. – М.: Ювента, 2013.









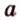
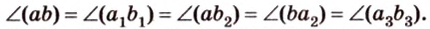
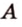 прямой
прямой 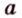
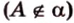 ;
;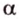
 ;
; и
и  прямую
прямую 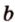 .
.