Как найти расстояние от хорды до дуги

Круговой сегмент — часть круга ограниченная дугой и секущей (хордой).

На рисунке:
L — длина дуги сегмента
c — хорда
R — радиус
a — угол сегмента
h — высота

Первый калькулятор рассчитывает параметры сегмента, если известен радиус и угол по следующим формулам:

Формулы вычисления параметров сегмента

Площадь сегмента:
[1]
Длина дуги:

Длина хорды:

Высота сегмента:

Однако, как справедливо заметил наш пользователь:«на практике часто случается, что как радиус дуги, так и угол неизвестны» (см. длина дуги ). Для этого случая для расчета площади сегмента и длины дуги можно использовать следующий калькулятор:

Калькулятор вычисляет радиус круга по длине хорды и высоте сегмента по следующей формуле:

Далее, зная радиус и длину хорды, легко найти угол сегмента по формуле:

Остальные параметры сегмента вычисляются аналогично первому калькулятору, по формулам, приведенным в начале статьи.

Следующий калькулятор вычисляет площадь сегмента по высоте и радиусу:

Этот калькулятор вычисляет угол из высоты и радиуса по следующей формуле:

далее используется формула [1] для получения площади.

15 вычислений по сегменту круга в одной программе

Последний калькулятор включает в себя все оставшиеся вычисления параметров кругового сегмента:

• длина дуги
• угол
• хорда
• высота
• радиус
• площадь

Выберите два известных аргумента и калькулятор выдаст вам все оставшиеся.

Расстояние от центра окружности до хорды

Рассмотрим, как найти расстояние от центра окружности до хорды.

Расстояние от точки до прямой измеряется длиной перпендикуляра, опущенного из этой точки на данную прямую. Значит, расстояние от центра окружности до хорды равно длине перпендикуляра, проведённого из центра окружности к этой хорде.

Например, расстояние от точки O — центра окружности — до хорды AB равно длине перпендикуляра OF:

Отрезки AB и CD являются хордами окружности. Найти расстояние от центра окружности до хорды CD, если AB=24, CD=10, а расстояние от центра окружности до хорды AB равно 5.

Дано: окружность (O; R), AB и CD — хорды,

1) Соединим центр окружности с концами хорд.

2) Треугольники AOB и COD — равнобедренные с основаниями AB и CD (AO=BO=CO=DO как радиусы).

Значит, их высоты OF и OK являются также медианами. Следовательно,

3) Рассмотрим треугольник AOF, где ∠AFO=90 º.

4) Рассмотрим треугольник COK, где ∠CKO=90 º.

Сегмент круга

Вычисляет площадь, длину дуги, длину хорды, высоту и периметр сегмента круга. Описывается несколько вариантов расчета по параметрам сегмента — по углу, по хорде, по радиусу, по высоте и длине дуги.

Сегмент круга

Круговой сегмент — часть круга ограниченная дугой и секущей (хордой).

На рисунке:
L — длина дуги сегмента
c — хорда
R — радиус
a — угол сегмента
h — высота

Первый калькулятор рассчитывает параметры сегмента, если известен радиус и угол по следующим формулам:

Формулы вычисления параметров сегмента

Площадь сегмента:
[1]
Длина дуги:

Найти расстояние от хорды до окружности

Сегмент круга

Вычисляет площадь, длину дуги, длину хорды, высоту и периметр сегмента круга. Описывается несколько вариантов расчета по параметрам сегмента — по углу, по хорде, по радиусу, по высоте и длине дуги.

Сегмент круга

Круговой сегмент — часть круга ограниченная дугой и секущей (хордой).

На рисунке:
L — длина дуги сегмента
c — хорда
R — радиус
a — угол сегмента
h — высота

Первый калькулятор рассчитывает параметры сегмента, если известен радиус и угол по следующим формулам:

Формулы вычисления параметров сегмента

Площадь сегмента:
[1]
Длина дуги:

Расстояние от центра окружности до хорды

Рассмотрим, как найти расстояние от центра окружности до хорды.

Расстояние от точки до прямой измеряется длиной перпендикуляра, опущенного из этой точки на данную прямую. Значит, расстояние от центра окружности до хорды равно длине перпендикуляра, проведённого из центра окружности к этой хорде.

Например, расстояние от точки O — центра окружности — до хорды AB равно длине перпендикуляра OF:

Отрезки AB и CD являются хордами окружности. Найти расстояние от центра окружности до хорды CD, если AB=24, CD=10, а расстояние от центра окружности до хорды AB равно 5.

Дано: окружность (O; R), AB и CD — хорды,

1) Соединим центр окружности с концами хорд.

2) Треугольники AOB и COD — равнобедренные с основаниями AB и CD (AO=BO=CO=DO как радиусы).

Значит, их высоты OF и OK являются также медианами. Следовательно,

3) Рассмотрим треугольник AOF, где ∠AFO=90 º.

4) Рассмотрим треугольник COK, где ∠CKO=90 º.

Найти расстояние от хорды до окружности

Определение хорды

Хорда — это отрезок, который соединяет две точки заданной кривой. Хорда может быть у дуги, окружности, эллипса и т.д.
На рисунке хорда обозначена как отрезок AB красного цвета . Оба его конца находятся на окружности

Часть кривой, заключенной между двумя точками хорды, называется дугой.
На рисунке дуга хорды AB обозначена зеленым цветом .

Плоская фигура, заключенная между дугой и ее хордой называется сегментом.
Сегмент на рисунке ограничен красным отрезком AB с одной стороны, и зеленой дугой — с другой стороны.

Хорда, проходящая через центр окружности, называется диаметром окружности. Диаметр окружности — самая длинная хорда окружности.

Свойства хорды к окружности

• Если расстояния от центра окружности до хорд равны, то эти хорды равны. Верно и обратное — если хорды равны, то расстояния от центра окружности до этих хорд равны
• Если хорда больше, то расстояние от центра окружности до этой хорды меньше. Если хорда меньше, то расстояние от центра окружности до этой хорды больше. Верно и обратное
• Наибольшая возможная хорда является диаметром
• Серединный перпендикуляр к хорде проходит через центр окружности

• Если диаметр делит хорду, не являющуюся диаметром, пополам, то этот диаметр перпендикулярен этой хорде. Верно и обратное — если диаметр перпендикулярен хорде, то этот диаметр делит эту хорду пополам
• Если диаметр делит хорду, не являющуюся диаметром, пополам, то этот диаметр делит дуги, стягиваемые этой хордой, пополам. Верно и обратное — если диаметр делит дугу пополам, то этот диаметр делит пополам хорду, стягивающую эту дугу

• Если радиус делит хорду, не являющуюся диаметром, пополам, то этот радиус перпендикулярен этой хорде. Верно и обратное — если радиус перпендикулярен хорде, то этот радиус делит эту хорду пополам
• Если радиус делит хорду, не являющуюся диаметром, пополам, то этот радиус делит дугу, стягиваемую этой хордой, пополам. Верно и обратное — если радиус делит дугу пополам, то этот радиус делит пополам хорду, стягивающую эту дугу.
• Если радиус перпендикулярен хорде, то этот радиус делит дугу, стягиваемую этой хордой, пополам. Верно и обратное — если радиус делит дугу пополам, то этот радиус перпендикулярен хорде, стягивающей эту дугу.

Свойства хорды и вписанного угла

Свойства хорды и центрального угла

Формулы нахождения хорды

Обозначения в формулах:
l — длина хорды
α — величина центрального угла
R — радиус окружности
d — длина перпендикуляра, проведенного от центра окружности к хорде

Длина хорды окружности равна удвоенному радиусу данной окружности, умноженному на синус половины центрального угла.
Сумма квадрата половины длины хорды и квадрата перпендикуляра, проведенного к этой хорде, равна квадрату радиуса окружности. Данная формула следует из теоремы Пифагора.

Решение задач

Примечание. Если Вы не нашли решение подходящей задачи, пишите об этом в форуме. Наверняка, курс геометрии будет дополнен.

Задача.

Хорды АВ и СD пересекаются в точке S, при чем AS:SB = 2:3, DS = 12см, SC = 5см, найти АВ.

Решение.

Поскольку соотношение AS:SB = 2:3 , то пусть длина AS = 2x, SB = 3x

Согласно свойству хорд AS x SB = CS x SD, тогда

2х * 3х = 5 * 12
6х 2 = 60
х 2 = 10
x = √10

Откуда
AB = AS + SB
AB = 2√10 + 3√10= 5√10

Окружность разделена на части, которые относятся как 3,5:5,5:3 и точки деления соединены между собой. Определить величину углов образовавшегося треугольника.

Решение.
Обозначим коэффициент пропорциональности дуг окружности, как х. Соединим центры окружности с концами дуг. Поскольку центральный угол равен градусной мере дуги, на которую опирается, то соотношение центральных углов окружности будет равно соотношению ее частей (дуг).
Поскольку градусная мера окружности равна 360 градусам, то

3,5х + 5,5х + 3х = 360
12х = 360
х = 30

Откуда градусные величины центральных углов равны:
3 * 30 = 90
3,5 *30 = 105
5,5 *30 = 165

Углы образовавшегося треугольника являются углами, вписанными в окружность. Вписанный угол равен половине градусной меры дуги, на которую опирается.
Откуда углы треугольника равны:

90 / 2 = 45
105 / 2 = 52,5
165 / 2 = 82,5

Ответ: Величина углов треугольника равна 45 ; 52,5 ; 82,5 ;

Этот онлайн калькулятор вычисляет длину дуги кругового сегмента, где известны либо радиус и центральный угол сегмента, либо длина хорды и высота сегмента, либо радиус и высота сегмента. Самая полезная вещь, по моему мнению, это возможность находить длину дуги по длине хорды и высоте — эти переменные могут измеряться напрямую ( посмотрите на картинку — голубая часть — это круговой сегмент, его длину дуги мы ищем )

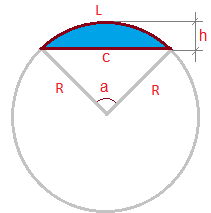
В калькуляторе ниже, выберите известные данные для нахождения длины дуги, введите их и получите результат. Все формулы, использованные для вычисления, перечислены под калькулятором.

Нахождение длины дуги по радиусу и центральному углу кругового сегмента

Формула очень проста

Нахождение длины дуги по длине хорды и высоте кругового сегмента

Здесь нужно вычислить радиус и центральный угол, а затем использовать формулу выше.

Радиус находится по формуле:

Центральный угол находится по формуле:

Нахождение длины дуги по радиусу и высоте кругового сегмента

Здесь нужно вычислить центральный угол, а затем снова использовать формулу:

Центральный угол находится по формуле:

Для других универсальных калькуляторов относительно кругового сегмента в общем, посмотрите калькулятор Сегмент круга . Этот калькулятор находит длину хорды, высоту сегмента, периметр сегмента, область сегмента и длину дуги; зависит от того, какие данные известны.

Перенесем начало координат в центр окружности. Пусть (x2,y2) — радиус вектор одного края хорды. (x0,y0) — радиус вектор точки на хорде откуда идет перпендикуляр до окружности. (x,y) — радиус вектор точки пересечения перпендикуляра с окружностью (их две), h — искомая высота, R — радиус окружности. Тогда используя теорему Пифагора для треугольника (x0,y0)-(x,y)-(x2,y2) получаем систему из трех уравнений.

(1) (x-x2)^2+(y-y2)^2=(x0-x2)^2+(y0-y2)^2+h^2;
(2) x^2+y^2=R^2;
(3) (x-x0)^2+(y-y0)^2=h^2;

…
3 уравнения, три неизвестные — h,x,y. Решаем и получаем достаточно громоздкие формулы. Приведу их, надеюсь не накосячил..

h^2=(p-y*t-x0)^2+(y-y0)^2;
где 
t=(y0-y2)/(x0-x2);
p=(x0^2+y0^2-x0*x2-y0*y2)/(x0-x2);
y=(p*t+-sqrt{R^2(t^2+1)-p^2})/(t^2+1);

находим два значения y, до ближайшей дуги и до дальней. До ближайшей будет меньшее значение.
Далее пусть хорда задается своим начальным (x2,y2) и конечным(x1,y1) значениями. Надо перебрать все возможные (x0,y0). Если поделить хорду на n частей то формула для (x0,y0) следующая

(x2+(k/n)*(x1-x2),y2+(k/n)*(y1-y2))

где k-целое пробегает значение от 1 до n-1. И в каждом таком (x0,y0) вычисляем h по вышеописанным формулам.