Ответ:
5
Объяснение:
1) Высота правильного треугольника рассчитывается по формуле:
h = (a√3) /2, где а — сторона правильного треугольника.
2) Высоты правильного треугольника являются его медианами, которые (во всех треугольниках) в точке пересечения делятся в отношении 2 : 1, считая от вершины.
Соответственно искомое расстояние равно:
2/3 · (5√3 · √3) / 2 = 5
Ответ: 5
Свойства равностороннего треугольника
Основные свойства равностороннего треугольника непосредственно следуют из свойств равнобедренного треугольника, частным случаем которого он является.
Свойства равностороннего треугольника
2) Высота, медиана и биссектриса, проведённые к каждой из сторон равностороннего треугольника, совпадают:
AK — высота, медиана и биссектриса, проведённые к стороне BC;
BF — высота, медиана и биссектриса, проведённые к стороне AC;
CD — высота, медиана и биссектриса, проведённые к стороне AB.
Длины всех трёх высот (медиан, биссектрис) равны между собой:
Если a — сторона треугольника, то
3) Точка пересечения высот, биссектрис и медиан называется центром правильного треугольника и является центром вписанной и описанной окружностей (то есть в равностороннем треугольнике центры вписанной и описанной окружностей совпадают).
4) Точка пересечения высот, биссектрис и медиан правильного треугольника делит каждую из них в отношении 2:1, считая от вершин:
5) Расстояние от точки пересечения высот, биссектрис и медиан
до любой вершины треугольника равно радиусу описанной окружности:
6) Расстояние от точки пересечения высот, биссектрис и медиан до любой стороны треугольника равно радиусу вписанной окружности:
7) Сумма радиусов вписанной и описанной окружностей правильного треугольника равна его высоте, медиане и биссектрисе: R+r=BF.

Центр треугольника
Треугольник — наиболее распространенная форма деталей в сферах машиностроения и строительства. Точка пересечения 3-х медиан считается центром треугольника. На эту точку приходится также центр тяжести и центр симметрии предметов треугольной формы. При разработке дизайнерских, инженерных проектов очень важно точно рассчитать центр тяжести элементов металлической или бетонной конструкции.
Существует несколько понятий центра для треугольника.
Инцентр — точка пересечения его биссектрис. Это — центр описанной около треугольника окружности.
Ортоцентр — точка пересечения его высот.
Центр тяжести,центр масс или центроид (обозн. М) — точка пересечения медиан треугольника.
Рассмотрим треугольник. Определим середины его сторон и соединим их с противолежащими углами. Точка пересечения медиан и будет центром тяжести тр-ка. Медиана делится этой точкой в пропорции 2:1 , (считая от вершины тр-ка).
Как найти центр треугольника
Если известны координаты его вершин, найдем сумму трех значений координат «х» и трех значений координат «у». Поделим каждую сумму на 3, получим среднее значение сумм координат «х» и «у», что и будет координатами центра тяжести.
Центром равностороннего треугольника является точка пересечения высот, биссектрис и медиан.
Центр равностороннего треугольника является также центром вписанной и описанной окружности.
Центроид расположен на отрезке, соединяющем ортоцентр и центр описанной окружности. Центроид делит отрезок 2:1.
Быстро найти центр треугольника G можно с помощью онлайн калькулятора. Для этого:
- ввести в поле калькулятора координаты вершин треугольника;
- нажать кнопку Вычислить. Калькулятор вычислит значение центра треугольника G.
Свойства равностороннего треугольника: теория и пример задачи
В данной статье мы рассмотрим определение и свойства равностороннего (правильного) треугольника. Также разберем пример решения задачи для закрепления теоретического материала.
Определение равностороннего треугольника
Равносторонним (или правильным) называется треугольник, в котором все стороны имеют одинаковую длину. Т.е. AB = BC = AC.
Примечание: правильный многоугольник – это выпуклый многоугольник, имеющий равные стороны и углы между ними.
Свойства равностороннего треугольника
Свойство 1
В равностороннем треугольнике все углы равны 60°. Т.е. α = β = γ = 60°.
Свойство 2
В равностороннем треугольнике высота, проведенная к любой из сторон, одновременно является биссектрисой угла, из которого она проведена, а также медианой и серединным перпендикуляром.
CD – медиана, высота и серединный перпендикуляр к стороне AB, а также биссектриса угла ACB.
Свойство 3
В равностороннем треугольнике биссектрисы, медианы, высоты и серединные перпендикуляры, проведенные ко всем сторонам, пересекаются в одной точке.
Свойство 4
Центры вписанной и описанной вокруг равностороннего треугольника окружностей совпадают и находятся на пересечении медиан, высот, биссектрис и серединных перпендикуляров.
Свойство 5
Радиус описанной вокруг равностороннего треугольника окружности в 2 раза больше радиуса вписанной окружности.
- R – радиус описанной окружности;
- r – радиус вписанной окружности;
- R = 2r.
Свойство 6
В равностороннем треугольнике, зная длину стороны (условно примем ее за “a”), можно вычислить:
1. Высоту/медиану/биссектрису:
2. Радиус вписанной окружности:
3. Радиус описанной окружности:
4. Периметр:
5. Площадь:
Пример задачи
Дан равносторонний треугольник, сторона которого равна 7 см. Найдите радиус описанной вокруг и вписанной окружности, а также, высоту фигуры.
Решение
Применим формулы, приведеные выше, для нахождения неизвестных величин:
Ответ:
5
Объяснение:
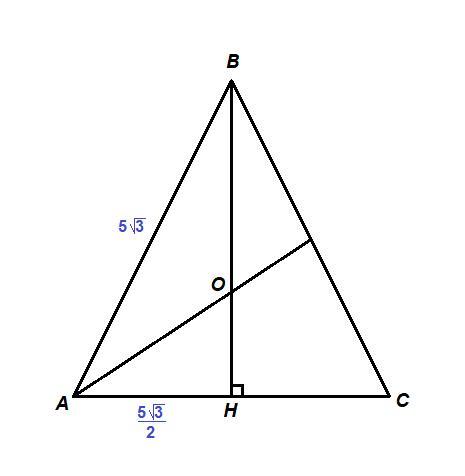
- Центр правильного треугольника — точка пересечения его медиан, которые совпадают с биссектрисами и высотами, — точка О.
ΔАВН: ∠АНВ = 90°,
По теореме Пифагора:
- Медианы треугольника точкой пересечения делятся в отношении 2 : 1 считая от вершины.
ВО : ОН = 2 : 1, значит
Так как центр правильного треугольника является центром описанной окружности (и вписанной тоже), то расстояние от точки О до всех вершин одинаково и равно 5.
——————————
Полезно запомнить формулы для правильного треугольника со стороной а:
высота:
радиус описанной окружности:
радиус вписанной окружности:
Приложения:
Ответ:
5
Объяснение:
- Центр правильного треугольника — точка пересечения его медиан, которые совпадают с биссектрисами и высотами, — точка О.
ΔАВН: ∠АНВ = 90°,
По теореме Пифагора:
- Медианы треугольника точкой пересечения делятся в отношении 2 : 1 считая от вершины.
ВО : ОН = 2 : 1, значит
Так как центр правильного треугольника является центром описанной окружности (и вписанной тоже), то расстояние от точки О до всех вершин одинаково и равно 5.
——————————
Полезно запомнить формулы для правильного треугольника со стороной а:
высота:
радиус описанной окружности:
радиус вписанной окружности:
Шар радиуса R касается всех сторон правильного треугольника со стороной a. Найдите расстояние от центра шара до плоскости треугольника
Задача из пособия: Погорелов А.В. 11 класс
21. Тела вращения
Решение
Далее
Смотрите также:






