Решение. Обозначим данный отрезок через АВ. По условию задачи АВ = т.
а) Пусть точки С и D делят отрезок АВ на три равные части, а М и N — середины крайних частей АС и DB (рис.30, а). Тогда MN =
= АВ- AM — NB. Но АС = CD = DB =m/3, следовательно,
АМ=1/2АС=m/b, NB=1/2 DB = m/6.
Таким образом, MN = m-m/6 -m/6= 2/3
б) Пусть точки Р, Q, R и S делят отрезок АВ на пять равных частей, а Е и F — середины крайних частей (рис.30, б). Тогда
EF = АВ — АЕ — FB, AP = SB = m/5, AE=m/10 FB = m/10
Таким образом,
EF = m-m/10-m/10=4/5m
Ответ, а)2/3m; б) 4/5m
Вопрос очень сложный. Но нужно попытаться найти ответ.
1 Итак, у нас есть весь отрезок: 84 см.
Назовем правую часть — П, Левую — Л, среднюю — С.
68 см = расстояние между серединами правой и левой частей. Значится, что туда входит:
Середина (С)+ 1/2П + 1/2Л. То есть, середина и по половине правой и левой части, поскольку это расстояние «между серединами» правой и левой частей.
Ну а вне этих 68 см находятся вторые половины правой (1/2П) и левой частей (Л).
2 Посчитаем совместную длину этих краев. Для этого вычтем из общей длины длину середины и внутренних половинок правой и левой частей:
84 см — 68 см (С+ 1/2П + 1/2Л)=16 см.
Итого общая длина внешних половинок правой и левой частей у нас = 16 см
3 Поскольку, что внутренние, что внешние половины правой и левой частей отрезка одинаковы (они же — половины), то общая длина их внутренних половинок тоже = 16 см
4 Тогда наши 68 см = С (середина) + 16 см (общая длина внутренних половинок правой и левой части)
Середина = 68 см — 16 см = 52 см
ГДЗ и решебники
вип уровня
- ГДЗ
- 7 класс
- Геометрия
- Атанасян
- Задание 77
Условие
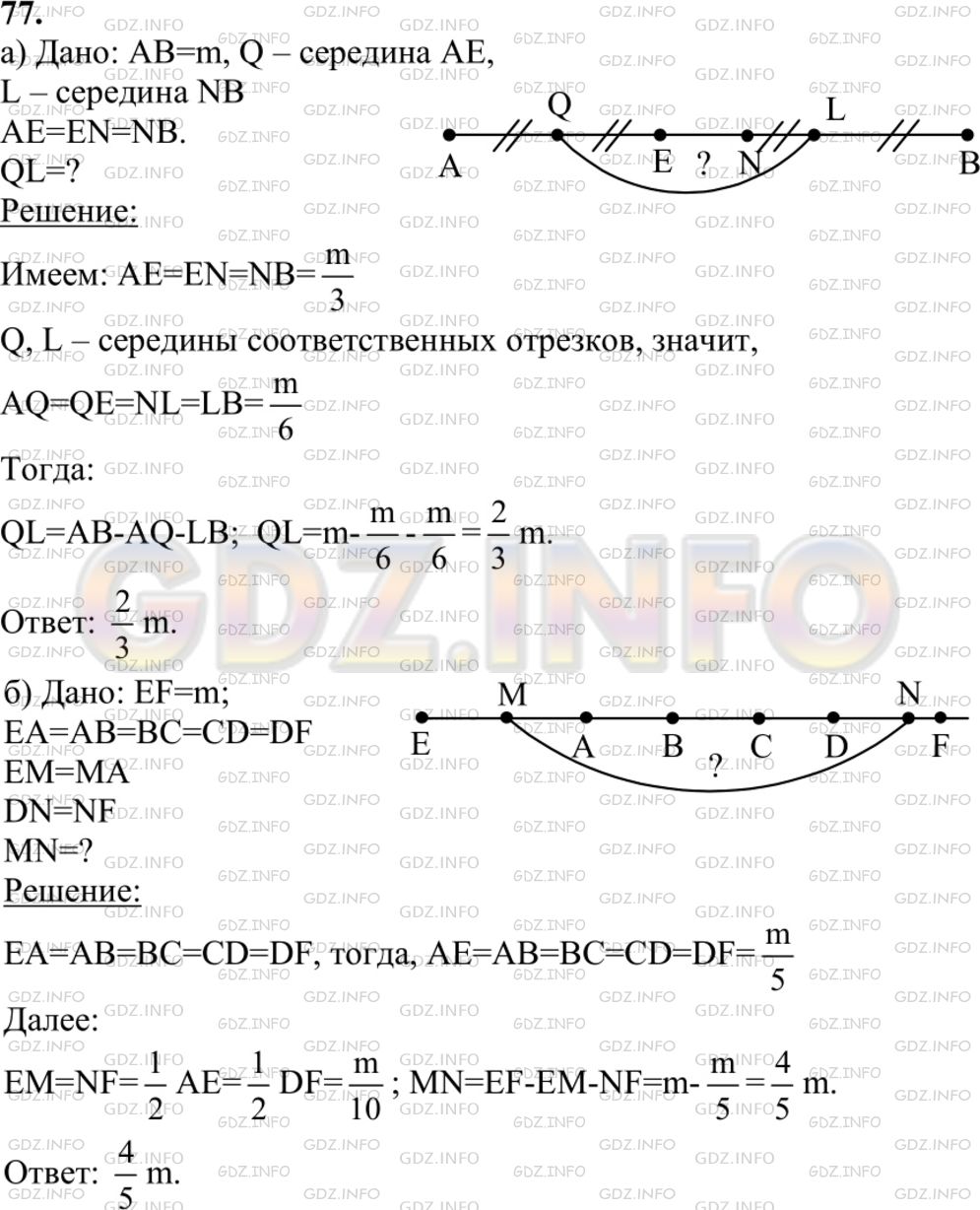
Отрезок длины т разделен: а) на три равные части; б) на пять равных частей. Найдите расстояние между серединами крайних частей.
Решение 1
Решение 2
Решение 3
Популярные решебники
Прочитаем задачу №77 для седьмого класса учебника Атанасян:
Отрезок длины m разделен: а) на три равные части; б) на пять равных частей. Найдите расстояние между серединами крайних частей.
а) Строим прямую AB, её длина равна m. По условию, прямая разделена на три равные части AC = CD = DB = 1/3m. Точки E и F — середины крайних отрезков. Следовательно AE = EC = DF = FB = AC : 2 (т.к. отрезки AC и DB равны). Зная длину всех отрезков, из которых состоит искомый отрезок EF (расстояние между серединами крайних отрезков), находим (см. чертеж в решении) EF = EC + CD + DF.
б) Строим прямую AB, её длина равна m. По условию, прямая разделена на пять равных частей AC = CD = DE = EF = FB = 1/5m. Точки K и M — середины крайних отрезков, следовательно AK = KC = FM = FB = AC : 2 = 1/10m (AC = FB). Зная длину всех отрезков, из которых состоит искомый отрезок KM (расстояние между серединами крайних отрезков), находим (см. чертеж в решении) KM = KC + CD + DE + EF + FM.
Найди верный ответ на вопрос ✅ «Отрезок длины 3,5 разделен на 5 равных частей. Найти расстояние между серединами крайних частей …» по предмету 📙 Геометрия, а если ответа нет или никто не дал верного ответа, то воспользуйся поиском и попробуй найти ответ среди похожих вопросов.
Искать другие ответы
Главная » Геометрия » Отрезок длины 3,5 разделен на 5 равных частей. Найти расстояние между серединами крайних частей