Свойства трапеции: отрезок, соединяющий середины диагоналей
Отрезок, соединяющий середины диагоналей трапеции, равен полуразности оснований.
Пусть точка М – середина диагонали АС, N – середина диагонали ВD, Р и Q – середины боковых сторон АВ и СD.
Тогда РМ – средняя линия треугольника АВС, РМ параллельна ВС. Это значит, что точка М лежит на средней линии РQ трапеции, поскольку через точку Р можно провести на плоскости единственную прямую, параллельную прямой ВС. При этом .
Аналогично, точка N – середина диагонали BD – также лежит на РQ, то есть на средней линии трапеции, и . Поскольку
,
.
Задача ЕГЭ по теме: «Отрезок, соединяющий середины диагоналей трапеции, равен полуразности оснований».
Основания трапеции равны 10 и 6. Найдите отрезок, соединяющий середины диагоналей трапеции.
Проведем PQ – среднюю линию трапеции, PQ = 8. Как мы доказали, отрезок MN, соединяющий середины диагоналей трапеции, лежит на средней линии.
PM – средняя линия треугольника ABC, значит, PM = 3.
NQ – средняя линия треугольника BCD, значит, NQ = 3.
Тогда MN = PQ − PM − NQ = 8 − 3 − 3 = 2
Ответ: 2.
Спасибо за то, что пользуйтесь нашими статьями.
Информация на странице «Свойства трапеции: отрезок, соединяющий середины диагоналей» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.
Публикация обновлена:
08.05.2023
math-public:srednyaya_liniya_trapecii
Содержание
Определение
Отрезок, соединяющий середины боковых сторон трапеции, называется
средней линией трапеции.
Свойства средней линии трапеции
Средняя линия трапеции параллельна основаниям трапеции и равна их
полусумме.
Доказательство
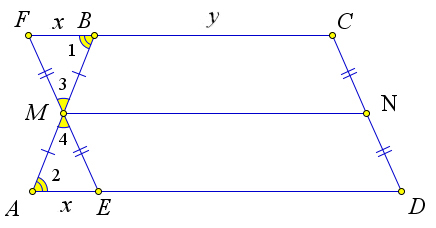
Рассмотрим трапецию $ABCD$, в которой проведена средняя линия $MN$.
Докажем, что $MNparallel AD$ и $MN=frac{AD+BC}{2}$.
Проведем через точку $M$ прямую $FE$ параллельно $CD$ ($Fin CB, Ein AD$).
Тогда $FCDE$ – параллелограмм ($FCparallel ED, FEparallel CD$).
Следовательно, $FE=CD$, $FC=ED$.
Кроме того $triangle FBM=triangle AME$, по второму признаку равенства ($angle
1=angle 2$, как накрест лежащие, $angle 3=angle 4$, как вертикальные,
$AM=MB$, так как $M$ – середина).
Следовательно, $FM=ME$.
Тогда $FMNC$ и $MNDE$ — параллелограммы ($FM=ME=ND=NC$ и $FEparallel
CD$).
Следовательно, $MNparallel BC$.
Кроме того, из равенства треугольников $triangle FBM=triangle AME$ следует,что $FB=AE$.
Пусть $FB=AE=x$ и $BC=y$.
Тогда $FC=ED=x+y$.
Следовательно, $MN=x+y$.
Кроме того, $BC+AD=BC+AE+ED=y+x+(x+y)=2x+2y$.
Таким образом, $MN=x+y=dfrac{BC+AD}{2}$.
Признаки средней линии трапеции
-
Пусть отрезок $MN$ соединяет точки на боковых сторонах трапеции. Если $M$ – середина боковой стороны, и $MN$ параллелен основаниям трапеции, то $MN$ – это средняя линия трапеции.
-
Пусть отрезок $MN$ соединяет точки на боковых сторонах трапеции. Если $MN$ параллелен основанием трапеции и равен их полусумме, то $MN$ – средняя линия трапеции.
Доказательство
Первый пункт теоремы является прямым следствием теоремы Фалеса.
Докажем второй пункт теоремы.
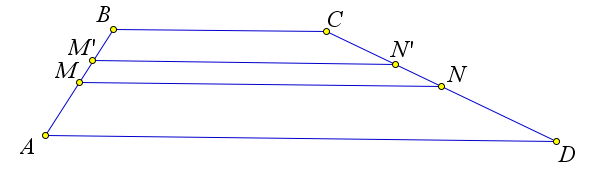
Рассмотрим трапецию $ABCD$, в которой на боковых сторонах $AB$ и $CD$ выбраны точки $M$ и $N$ соответственно, и при этом $MN=dfrac{AD+BC}{2}$.
Докажем, что тогда $MN$ – средняя линия трапеции $ABCD$.
Предположим противное, то есть $MN$ – не средняя линия данной трапеции.
Если ровно одна из точек $M$ или $N$ является серединой, то по первому пункту теоремы $MN$ – это средняя линия, так как $MN$ параллельна основаниям трапеции.
Пусть точки $M$ и $N$ – не середины боковых сторон.
Тогда пусть $M’N’$ – средняя линия трапеции.
Следовательно, $M’N’=frac{BC+AD}{2}=MN$ и $MNparallel BCparallel MN$.
Но тогда $MNN’M’$ – параллелограмм, и, следовательно, $MM’parallel NN’$, что противоречит тому, что $ABCD$ – это трапеция.
Следовательно, $MN$ – средняя линия.
Теорема (об отрезке, соединяющем середины диагоналей трапеции)
Отрезок, соединяющий середины диагоналей трапеции, равен
полуразности ее оснований.
Доказательство
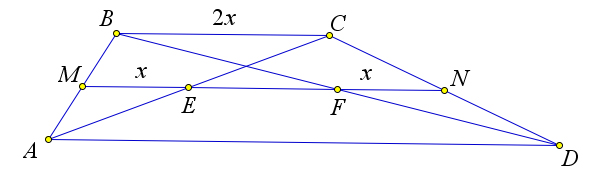
Рассмотрим трапецию $ABCD$, в которой точки $E$ и $F$ – это
середины диагоналей $AC$ и $BD$ соответственно.
Докажем, что $EF=frac{AD-BC}{2}$.
По теореме Фалеса средняя линия трапеции $MN$ делит диагонали $AC$ и $BD$ пополам, то есть точки $E$ и $F$ лежат на средней линии.
Тогда $ME$ и $FN$ – это средние линии треугольников $triangle ABC$ и $triangle DBC$.
Следовательно, если обозначить $BC=2x$, то $ME=FN=x$.
Тогда $EF=frac{2x+AD}{2}-x-x=frac{AD-2x}{2}=frac{AD-BC}{2}$.
· Последнее изменение: 2022/01/14 16:52 —
mesuslina
Ответ: MN = 2
Объяснение:
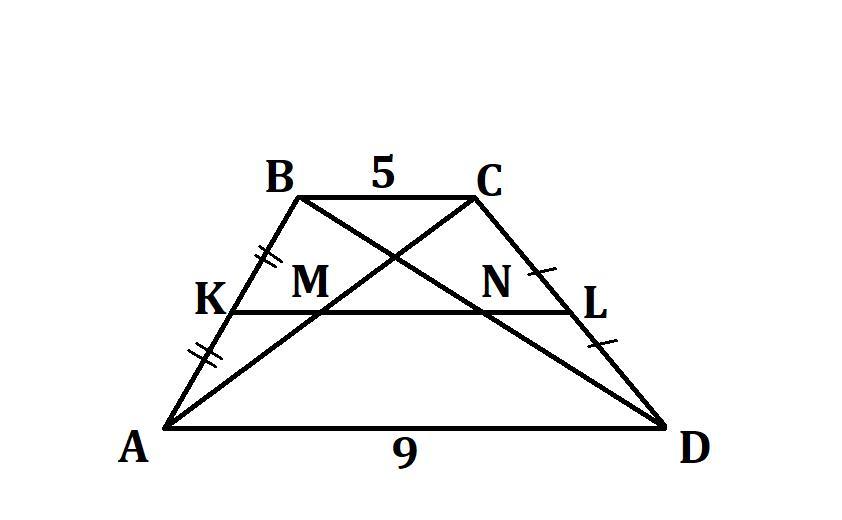
В трапеции ABCD известны основания AD = 9 и BC = 5. Найдите расстояние между серединами диагоналей трапеции (буквенное обозначение получившегося отрезка — MN).
**********
- Средняя линия трапеции проходит через середины диагоналей.
М – середина диагонали АС, N – середина диагонали ВD.
K и L – середины боковых сторон АВ и СD соответственно, то есть KL — средняя линия трапеции ABCD.
⇒ KМ – средняя линия ΔАВС, KM || BC.
⇒ М ∈ KL, поскольку через точку K можно провести на плоскости единственную прямую, параллельную прямой ВС.
KM = 1/2 · BC
Аналогично, N – середина диагонали BD, NL — средняя линия ΔDCB, NL || BC, N ∈ KL.
NL = 1/2 · BC
По свойству средней линии трапеции,
#SPJ3
Приложения:
2018-12-06
Расстояние между серединами диагоналей трапеции равно 5 см, а ее боковые стороны имеют длины 6 см и 8 см. Найдите расстояние между серединами оснований.
Решение:
Пусть $ABCD$ — данная трапеция, $M$ и $K$ — середины диагоналей (см. рис. а).
Через точку $B$ проведем прямую, параллельную $CD$, которая пересекает основание $AD$ в точке $E$. Так как $BCDE$ — параллелограмм, то $BE = CD = 8 см$. Тогда $AE = AD — ED = AD — BC$. Используем, что $MK = 0,5(AD — BC)$. (Этот факт можно доказать, продолжив отрезок $MK$, лежащий на средней линии трапеции, до пересечения с одной из боковых сторон трапеции. Если $N$ — точка пересечения, то отрезки $KN$ и $MN$ являются средними линиями треугольников $ABD$ и $ABC$ соответственно.) По условию, $MK = 5 см$, значит, $AE = 10 см$. В треугольнике $ABE$ длины сторон равны б см, 8 см и 10 см, значит, $Delta ABE$ — прямоугольный с прямым углом $B$ (по теореме, обратной теореме Пифагора). Пусть $P$ и $Q$ — середины оснований $BC$ и $AD$ соответственно. Вычислить длину $PQ$ можно различными способами.
Первый способ. Рассмотрим четырехугольник $PKQM$ (см. рис. б). Его противолежащие стороны $PM$ и $KQ$ являются средними линиями треугольников $ABC$ и $ABD$ соответственно, значит, $PKQM$ — параллелограмм. Так как $PM parallel AB, PK parallel CD parallel BE$ и $AB perp BE$, то $PM perp PK$, то есть, $PKQM$ — прямоугольник. Диагонали прямоугольника равны, следовательно, $PQ = MK = 5 см$.
Второй способ. Продолжим боковые стороны трапеции до пересечения в точке $F$ (см. рис. в) и используем известный факт: прямая, проходящая через середины оснований трапеции содержит точку пересечения прямых, содержащих боковые стороны (его можно доказать, используя либо векторы, либо подобие треугольников, либо гомотетию). По ранее доказанному, $angle AFD = 90^{ circ}$, следовательно, точки $P$ и $Q$ являются центрами описанных окружностей для прямоугольных треугольников $BFC$ и $AFD$ соответственно. Значит, $QF$ и $PF$ — радиусы этих окружностей, поэтому, $PQ = QF — PF = 0,5AD — 0,5BC = 0,5(AD — BC) = 5 (см)$.
Ответ: 5 см.
[19.09.2017 18:01]
Решение 15523:
Номер задачи на нашем сайте: 15523
ГДЗ из решебника:
Тема:
Планиметрия
Трапеция
Нашли ошибку? Сообщите в комментариях (внизу страницы)
|
Раздел: Геометрия Полное условие: 4.10. Основания трапеции равны a и b (a > b). Найдите длину отрезка, соединяющего середины диагоналей трапеции.Решение, ответ задачи 15523 из ГДЗ и решебников: Этот учебный материал представлен 1 способом:
|
||
| Счетчики: 5229 | Добавил: Admin |
| Добавить комментарий
Добавлять комментарии могут только зарегистрированные пользователи. [ Регистрация | Вход ] |






 Для просмотра в натуральную величину нажмите на картинку
Для просмотра в натуральную величину нажмите на картинку