11.212_Расстояние между непересекающимися диагоналями
| 26.11.2013, 17:51 | |
| Расстояние между непересекающимися диагоналями двух смежных боковых граней куба равно d. Определить полную поверхность куба.
|
|
Категория: Задачи стереометрии | Добавил: alexlat |
|
| Просмотров: 1398 | Загрузок: 0
| Рейтинг: 0.0/0 |
Добавлять комментарии могут только зарегистрированные пользователи.
[
Регистрация
|
Вход
]
Статистика
2019-03-19
Найти расстояние между двумя непересекающимися диагоналями смежных граней куба, ребро которого равно $а$.
Решение:
Пусть выбраны диагонали $C_1D$ и $B_1C$ (рис.). Так как $B_1C parallel A_1D$ и $C_1D parallel B_1A$, то плоскости $A_1C_1D$ и $AB_1C$ параллельны. Расстояние между $B_1C$ и $C_1D$ равно расстоянию между этими плоскостями.
Обе плоскости $A_1C_1D$ и $AB_1C$ перпендикулярны к диагонали $BD_1$.
Поэтому искомое расстояние равно разности между отрезком $BD_1$ и удвоенной высотой пирамиды $D_1A_1C_1D$. Объем этой пирамиды равен $frac{a^3}{6}$, а площадь основания $A_1C_1D$ равна $frac {a^2 sqrt {3}}{2}$, следовательно, высота $h = frac{a}{ sqrt {3}}$. Так как $BD_1 = a sqrt {3}$, то искомое расстояние равно $a sqrt {3} — frac{2a}{ sqrt{3}} = frac{a}{ sqrt {3}}$.
Ответ. $frac{a}{ sqrt {3}}$.
Противоположные грани куба параллельны.
Значит расстоянием между скрещивающимися диагоналями противоположных граней (АВ₁ и D₁C) будет расстояние между параллельными плоскостями — перпендикуляр, проведенный из любой точки одной плоскости к другой.
Ребро AD перпендикулярно боковым граням АВВ₁А₁ и DCC₁D₁.
Значит, АD — расстояние между параллельными плоскостями АВВ₁А₁ и DCC₁D₁. Следовательно
расстояние между прямыми АВ₁ и D₁C равно а.
Скачать материал

Скачать материал


- Сейчас обучается 39 человек из 27 регионов






Описание презентации по отдельным слайдам:
-
1 слайд
(типовые задания С2) — 4
Многогранники:
виды задач и методы их решения
Методическая разработка Амачкиной А.А.
МОУ СОШ №12,
г. Балашиха, Московской области. -
2 слайд
Для нахождения расстояния между скрещивающимися прямыми можно воспользоваться одним из приведенных ниже четырех способов.
1. Построить общий перпендикуляр двух скрещивающихся прямых (отрезок с концами на этих прямых и перпендикулярный обеим) и найти его длину.Расстояние между двумя скрещивающимися прямыми равно длине отрезка их общего перпендикуляра.
1.4. Расстояние между
скрещивающимися прямыми
Поэтапно-вычислительный метод -
3 слайд
2. Построить плоскость, содержащую одну из прямых и параллельную второй.
Тогда искомое расстояние будет равно расстояние от какой-нибудь точки второй прямой до построенной плоскости.
3. Заключить данные прямые в параллельные плоскости, проходящие через
данные скрещивающиеся прямые, и найти расстояние между этими плоскостями.
4. Построить плоскость, перпендикулярную одной из данных прямых, и построить на этой плоскости ортогональную проекцию второй прямой -
-
5 слайд
Пример 19. В кубе, длина ребра которого равна a, найти расстояние между ребром и диагональю, не пересекающей его грани.
Решение. В качестве примера найдем расстояние между ребром AA1 и диагональю D1C .Прямые AA1 и D1C — скрещивающиеся. Используя каждый из отмеченных способов, покажем, что расстояние между ними равно a . -
6 слайд
1-й способ.
Так как
то A1D1 –общий перпендикуляр двух скрещивающихся прямых AA1 и D1C . Расстояние между AA1 и DD1C1 равно A1D1 = a
А
C
А1
B1
C1
D1
B
D -
7 слайд
2-й способ. Так как
плоскость DD1C1 , содержащая D1C , параллельна AA1 , то расстояние от AA1
до DD1C1 равно a .
А
C
А1
B1
C1
D1
B
D -
8 слайд
А
C
А1
B1
C1
D1
B
D
3-й способ. Плоскость
DD1C1 , содержащая , D1 C параллельна
плоскости AA1B1 , содержащей , AA1 и
Расстояние между ними равно a . -
9 слайд
А
C
А1
B1
C1
D1
B
D
4-й способ. Плоскость
ABC перпендикулярна прямой . AA1 Точка A-проекция AA1 на эту плоскость.
Проекцией D1C на плоскость ABC является DC. Расстояние от точки A до DC. равно a . -
10 слайд
Пример 20. Найти расстояние между непересекающимися диагоналями двух смежных граней куба, длина ребра которого равна a .
Решение. Найдем расстояние между диагоналями A1C1 и AD1 куба
ABCDA1 B1 C1 D1 . -
11 слайд
А
C
А1
B1
C1
D1
B
D
Q
K
P
N
1-й способ. Пусть отрезок PQ есть общий перпендикуляр скрещивающихся прямых A1C1 и AD1 , а PN и KQ — его ортогональные проекции на плоскости A1B1C1 и AA1D1 соответственно
На основании теоремы о трех перпендикулярах -
12 слайд
Треугольники A1PN и KQD1 — прямоугольные и равнобедренные, поэтому
Тогда из прямоугольного треугольника PNQ получим расстояние между A1C1 и AD1: -
13 слайд
2-й способ. Построим плоскость, содержащую AD1 и параллельную A1C1 .Искомой плоскостью является AD1C Найдем расстояние до нее от какой-либо точки прямой A1C1 . Для этого опустим из точки O на указанную плоскость перпендикуляр. Плоскости BB1D1 и AD1C перпендикулярны
C
C1
B1
А
А1
D1
B
D
O1
O
N
B1
B
O
O1
D
D1
N -
14 слайд
Замечание. Для нахождения расстояния от точки О до плоскости AD1C можно воспользоваться результатом примера 10.
-
15 слайд
3-й способ. Построим параллельные плоскости AD1C и BA1C1 содержащие прямые AD1 и A1C1 соответственно. Диагональ B1D куба перпендикулярна обеим плоскостям и точками K и N делится на три равные части (опорная задача 20). Расстояние между плоскостями AD1C и BA1C1 равно длине
отрезка KN, т.е.
N
C
C1
B1
А
А1
D1
B
D
O1
O
N
K
B1
B
O
O1
D
D1
N
K -
16 слайд
4-й способ. Плоскость BB1D1 перпендикулярна прямой A1C1и плоскости
AD1C
C
C1
B1
А
А1
D1
B
D
O1
O
N
B1
B
O
O1
D
D1
N -
17 слайд
D1O1 — проекция AD1 на плоскость BB1D1 . Расстояние от точки O (проекции A1C1 на плоскость BB1D1 ) до D1O1 равно длине отрезка
ON
Пример 21. В правильной усеченной четырехугольной пирамиде ABCDA1 B1 C1 D1
со сторонами оснований равными a и b( a > b ), и высотой h найти расстояние между диагональю BD1 и диагональю большего основания AC . -
18 слайд
А
B1
D
C
B
O
K
C1
D1
A1
O1
B1
D1
B
D
N
O
K
Решение. Прямые BD1 и AC скрещиваются.Точки O и O1 — точки пересечения диагоналей оснований пирамиды.
как отрезок, соединяющий середины оснований
равнобедренных трапеций BB1D1D и AA1C1C. -
19 слайд
так как AC перпендикулярна двум
Построим плоскость перпендикулярную одной из скрещивающихся прямых BD1 и AC . Плоскость
пересекающимся прямым этой плоскости:
( ABCD — квадрат) и (OO1 — высота пирамиды). Прямая BD1 лежит в плоскости BB1D1 , поэтому искомое расстояние равно длине перпендикуляра, опущенного из точки O на BD1 .
OK найдем из подобия прямоугольных треугольников BD N 1 и BKO, имеющих общий острый угол. В треугольнике BD N 1 : D1N = h , -
-
21 слайд
Пример 22. В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, найти расстояние между прямыми BD и SA.
Решение. Пусть E – основание перпендикуляра, опущенного из точки O на ребро SA. Так как прямая BD перпендикулярна плоскости AOS, то
А
E
B
S
C
D
O -
22 слайд
Таким образом, ОЕ – общий перпендикуляр к скрещивающимся прямым BD и SA. Найдем его длину, вычислив двумя способами площадь треугольника AOS. Из равенства AO* SO = AS *OE, где
Пример 23. В единичном кубе ABCDA1B1C1D1 найти расстояние между диагональю куба BD1 и диагональю грани AB1 .
Решение. Введем прямоугольную систему координат, тогда А(0; 0; 0) , В(0;1; 0) , В1(0;1;1), D1 (1; 0;1).
Bекторно-координатный метод -
23 слайд
Пусть EF – общий перпендикуляр скрещивающихся прямых BD1 и AB1 , то есть
ПричемОбозначим
А
D
C
x
z
E
А1
B1
C1
D1
B
y
F
и воспользуемся формулами для
координат точки (опорная задача 1), которая делит данный отрезок в заданном
отношении. -
24 слайд
Тогда E(0, p, p) , F(q, 1- q, q) . Так как вектор
должен быть перпендикулярным векторам
то имеем систему уравнений: -
25 слайд
В1
А
А1
В
N
D
С
D1
С1
M
Пример 24. В единичном кубе ABCDA1B1C1D1 найти расстояние между прямыми AB1 и BD .
Решение. Пусть
Если M и N – основания общего перпендикуляра прямых AB1и BD соответственно, то имеем
Векторный метод -
26 слайд
Вектор
поэтому имеем -
-
28 слайд
Если AB и CD – скрещивающиеся ребра треугольной пирамиды ABCD, d – расстояние между ними, АВ = а ,
CD =b ,– угол между AB и CD, V – объем пирамидыABCD, то
Пример 25. В единичном кубе ABCDA1 B1 C1 D1 найти расстояние между диагональю куба BD1 и диагональю грани AB1 .
Решение. Найдем искомое расстояние по формуле
Опорная задача -
29 слайд
где V –объем пирамиды ABB1 D1
— угол между прямыми
BD1 и AB1 . Так как площадь основания АВВ1 пирамиды
ABB1 D1 равна
В1
А
А1
В
D
С
D1
С1 -
30 слайд
Используемая литература:
Корянов А.Г., Прокофьев А.А. Многогранники: виды задач и методы их решения.
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 265 405 материалов в базе
- Выберите категорию:
- Выберите учебник и тему
- Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Материал подходит для УМК
-
«Математика: алгебра и начала математического анализа, геометрия. Геометрия (базовый и углубленный уровни)», Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др.
Тема
Глава 3. Многогранники
Больше материалов по этой теме
Другие материалы
Решение типовых заданий ЕГЭ второй части задание 14-3
- Учебник: «Математика: алгебра и начала математического анализа, геометрия. Геометрия (базовый и углубленный уровни)», Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др.
- Тема: Глава 3. Многогранники
- 13.04.2018
- 1348
- 9

Решение типовых заданий ЕГЭ второй части задание 14-2
- Учебник: «Математика: алгебра и начала математического анализа, геометрия. Геометрия (базовый и углубленный уровни)», Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др.
- Тема: Глава 3. Многогранники
- 13.04.2018
- 982
- 2



Самостоятельная работа по теме «Цилиндр» 11 класс.
- Учебник: «Математика: алгебра и начала математического анализа, геометрия. Геометрия (базовый и углубленный уровни)», Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др.
- Тема: Глава 3. Многогранники
Рейтинг:
5 из 5
- 01.04.2018
- 1768
- 5

Презентация по математике на тему «Многогранники»
- Учебник: «Математика: алгебра и начала математического анализа, геометрия. Геометрия (базовый и углубленный уровни)», Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др.
- Тема: Глава 3. Многогранники
- 28.03.2018
- 740
- 0

Контрольная работа «Многогранники» 10 класс
- Учебник: «Математика: алгебра и начала математического анализа, геометрия. Геометрия (базовый и углубленный уровни)», Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др.
- Тема: Глава 3. Многогранники
- 27.03.2018
- 1140
- 1


Вам будут интересны эти курсы:
-
Курс повышения квалификации «Изучение вероятностно-стохастической линии в школьном курсе математики в условиях перехода к новым образовательным стандартам»
-
Курс профессиональной переподготовки «Экономика: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Особенности подготовки к сдаче ОГЭ по математике в условиях реализации ФГОС ООО»
-
Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО»
-
Курс профессиональной переподготовки «Организация деятельности помощника-референта руководителя со знанием иностранных языков»
-
Курс профессиональной переподготовки «Черчение: теория и методика преподавания в образовательной организации»
-
Курс профессиональной переподготовки «Организация технической поддержки клиентов при установке и эксплуатации информационно-коммуникационных систем»
-
Курс повышения квалификации «Учебная деятельность по предметной области «Черчение»: основы предмета и реализация обучения в условиях ФГОС»
-
Курс повышения квалификации «Финансовые инструменты»
-
Курс профессиональной переподготовки «Эксплуатация и обслуживание общего имущества многоквартирного дома»
-
Курс профессиональной переподготовки «Гражданско-правовые дисциплины: теория и методика преподавания в образовательной организации»
Сообщения без ответов | Активные темы
| Автор | Сообщение | ||
|---|---|---|---|
|
|||
|
Измерения прямоугольного параллелепи-
|
||
| Вернуться к началу |
|
||
|
revos |
Заголовок сообщения: Re: Сложная стереометрическая задача №272
|
|
. Последний раз редактировалось revos 16 фев 2023, 20:47, всего редактировалось 1 раз. |
|
| Вернуться к началу |
|
|
revos |
Заголовок сообщения: Re: Сложная стереометрическая задача №272
|
|
Mikiloy писал(а): Измерения прямоугольного параллелепи- Решать задачу как «стереометрическую» (это, как я понимаю , с геометрическими построениями и доказательствами, с использованием теорем типа» о трёх перпендикулярах»…. нет никакого желания). Кстати, номер задачи ни о чём мне не говорит.)
|
|
| Вернуться к началу |
|
|
Exzellenz |
|
||
|
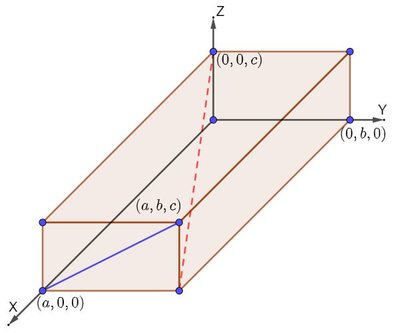
Уравнение синей диагонали: [math]vec{X}=begin{pmatrix} a \ 0 \ 0 end{pmatrix}+rbegin{pmatrix} 0 \ b \ c end{pmatrix}[/math] Уравнение красной диагонали: [math]vec{X}=begin{pmatrix} 0 \ 0 \ c end{pmatrix}+sbegin{pmatrix} a \ b \ -c end{pmatrix}[/math] [math]d=frac{left( vec{S_2}-vec{S_1} right) cdot left[ vec{R_1} times vec{R_2}right] }{left| vec{R_1} times vec{R_2} right| }=frac{ begin{pmatrix} -a \ 0 \ c end{pmatrix} cdot begin{pmatrix} -2bc \ ac \ -ab end{pmatrix} }{sqrt{4b^2c^2+a^2c^2+a^2b^2} }=frac{abc}{sqrt{4b^2c^2+a^2c^2+a^2b^2}}[/math] Последний раз редактировалось Exzellenz 16 фев 2023, 20:20, всего редактировалось 1 раз. |
|||
| Вернуться к началу |
|
||
|
Niemand |
|
||
|
[math]pc=a^2;[/math] [math]qc=b^2;[/math] [math]frac{1}{a^2}+frac{1}{b^2} =frac{1}{pc}+frac{1}{qc}=frac{q+p}{pqc}=frac{c}{pqc}=frac{1}{pq}=frac{1}{h^2}[/math]
|
|||
| Вернуться к началу |
|
||
| За это сообщение пользователю Niemand «Спасибо» сказали: Exzellenz |
|||
| Похожие темы | Автор | Ответы | Просмотры | Последнее сообщение |
|---|---|---|---|---|
|
Стереометрическая задача на призму
в форуме Геометрия |
Rollick |
5 |
915 |
12 дек 2018, 08:57 |
|
Стереометрическая задача (14 формат ЕГЭ)
в форуме Геометрия |
Ariurn |
1 |
356 |
18 дек 2015, 10:05 |
|
Некорректная стереометрическая задача из ЕГЭ 2020 ? ДВ
в форуме Геометрия |
random user |
35 |
789 |
11 июл 2020, 09:48 |
|
Сложная задача
в форуме Теория вероятностей |
galachel |
7 |
1129 |
19 дек 2015, 20:41 |
|
Сложная задача
в форуме Механика |
Arsenal |
1 |
1007 |
02 мар 2014, 11:19 |
|
Сложная задача
в форуме Начала анализа и Другие разделы школьной математики |
olegog |
10 |
887 |
14 июл 2015, 12:54 |
|
Сложная задача
в форуме Геометрия |
Pazuiorstv |
1 |
544 |
15 май 2014, 21:53 |
|
Сложная задача
в форуме Алгебра |
lemur |
3 |
170 |
25 ноя 2021, 14:43 |
|
Сложная задача
в форуме Интересные задачи участников форума MHP |
artron |
3 |
638 |
23 авг 2013, 13:52 |
|
Сложная задача
в форуме Алгебра |
Alexsander |
1 |
483 |
21 фев 2016, 15:11 |
Кто сейчас на конференции |
|
Сейчас этот форум просматривают: нет зарегистрированных пользователей и гости: 5 |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |





































 Да, я чего-то наврал. Хотел исправить, но несколько дней сайт был недоступен.
Да, я чего-то наврал. Хотел исправить, но несколько дней сайт был недоступен.