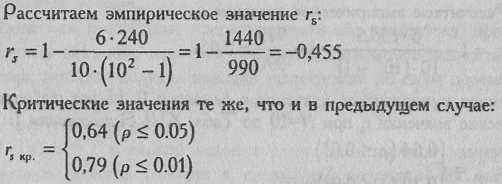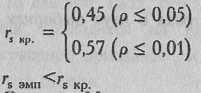Загрузить PDF
Загрузить PDF
Коэффициент корреляции ранга Спирмена позволяет определить, существует ли между двумя переменными зависимость, выражаемая монотонной функцией (то есть при росте одной переменной увеличивается и вторая, и наоборот). Приведенные в статье простые шаги позволят вам производить расчеты вручную, а также вычислять коэффициент корреляции при помощи программ Excel и R.
-
1
Составьте таблицу данных. Таким образом вы упорядочите информацию, необходимую для расчета коэффициента корреляции ранга Спирмена. При этом вам понадобится:
- 6 колонок, озаглавленных так, как показано выше на рисунке.
- Количество строк, соответствующее числу пар переменных.
-
2
Заполните первые две колонки парами переменных.
-
3
В третьей колонке запишите номера (ранги) пар переменных от 1 до n (общее число пар). Присвойте номер 1 паре с наименьшим значением в первой колонке, 2 — следующему за ним значению, и так по возрастанию величин переменной из первой колонки.
-
4
В четвертой колонке сделайте то же, что и в третьей, но на этот раз пронумеруйте пары переменных по второй колонке таблицы.
-
Если два (или более) значения переменной в одной колонке одинаковы, расположите их один за другим и найдите среднее значение их номеров, затем пронумеруйте их этим средним значением.
В приведенном справа примере два значения переменной совпадают и равны 5; в случае нормальной нумерации эти данные получили бы ранги 2 и 3. Поскольку значения одинаковы, находим среднюю величину их рангов. Среднее 2 и 3 равно 2,5, поэтому обеим величинам присваиваем ранг 2,5.
-
-
5
В колонке «d» вычислите разность между двумя рангами из предыдущих двух колонок. Например, если ранг в третьей колонке равен 1, а в четвертой – 3, то разница между ними составит 2. Знак не имеет значения, поскольку на следующем шаге эти числа будут возведены в квадрат.
-
6
Возведите каждое значение из колонки «d» в квадрат и запишите полученные величины в колонку «d2«.
-
7
Просуммируйте все значения из колонки «d2«. Вы определите сумму Σd2.
-
8
Воспользуйтесь одной из следующих формул:
-
9
Проанализируйте результат. Полученное значение находится между -1 и 1.
- Если оно близко к -1, корреляция отрицательна.
- Если близко к 0, корреляция отсутствует.
- Если близко к 1, наблюдается положительная корреляция.
- Не забудьте поделить на сумму переменных и взять корень. После этого поделите на Σd2.
Реклама
-
1
Создайте новые колонки с рангами, соответствующими колонкам данных. Например, если данные внесены в Колонку A2:A11, используйте функцию «=RANK(A2,A$2:A$11)» и занесите результаты для всех строк в новую колонку.
-
2
Найдите ранги для одинаковых величин, как описано в шагах 3 и 4 метода 1.
-
3
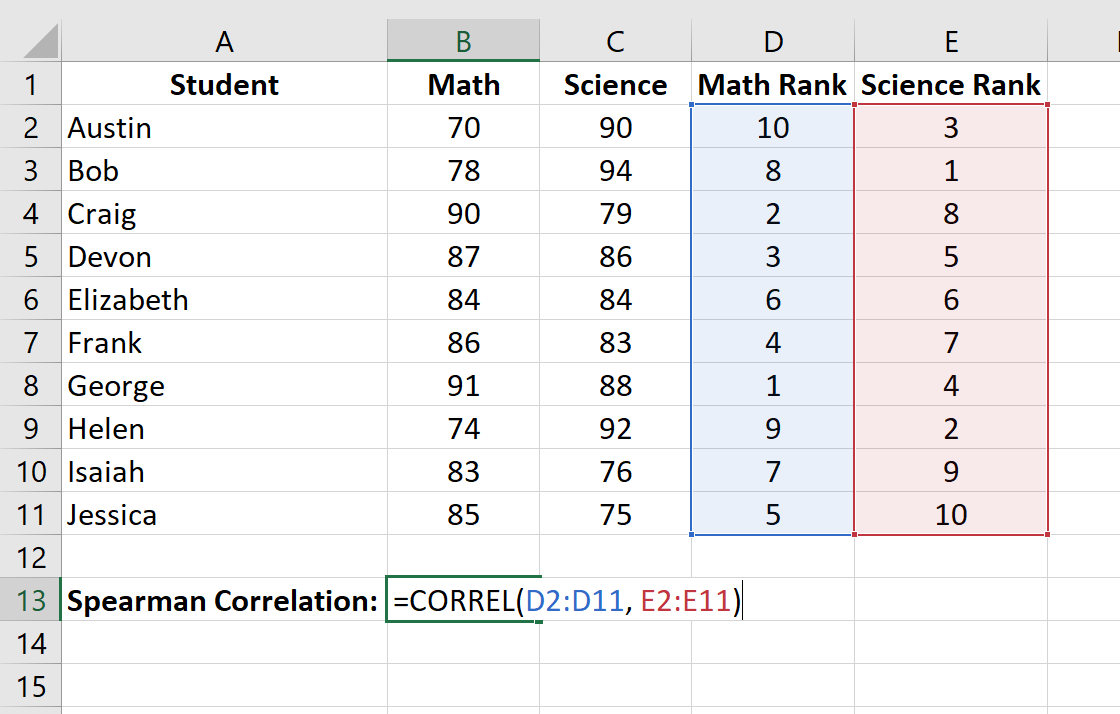
В новой ячейке определите корреляцию между двумя колонками рангов с помощью функции «=CORREL(C2:C11,D2:D11)». В данном случае C и D – это колонки, содержащие ранги. Таким образом, в данной ячейке вы получите коэффициент ранговой корреляции Спирмена.
Реклама
-
1
Если у вас еще нет программы R для обработки статистических данных, приобретите ее (см. http://www.r-project.org).
-
2
Сохраните данные в формате CSV, расположив их в двух колонках, корреляцию между которыми вы собираетесь исследовать. Сохранить файл в данном формате легко посредством опции «Сохранить как».
-
3
Откройте редактор R. Если вы еще не вошли в программу R, просто запустите ее. Для этого достаточно нажать иконку R на рабочем столе.
-
4
Наберите команды:
- d <- read.csv(«NAME_OF_YOUR_CSV.csv») и нажмите клавишу ввода
- cor(rank(d[,1]),rank(d[,2]))
Реклама
Советы
- Как правило, набор данных должен состоять не менее чем из 5 пар для того, чтобы можно было достоверно установить какую-либо корреляцию (3 пары было использовано в примере выше для простоты).
Реклама
Предупреждения
- Коэффициент ранговой корреляции Спирмена позволяет установить лишь то, растут ли обе переменные или уменьшаются одновременно. Если разброс данных слишком велик, этот коэффициент не даст точного значения корреляции.
- Приведенная функция даст верный результат при отсутствии одинаковых значений в массиве данных. Если такие значения существуют, как в рассмотренном нами примере, необходимо использовать следующее определение: коэффициент корреляции, основанный на рангах.
Реклама
Об этой статье
Эту страницу просматривали 68 902 раза.
Была ли эта статья полезной?
Коэффициент корреляции Спирмена: Определение
Коэффициент ранговой корреляции Спирмена или коэффициент корреляции Спирмена — это непараметрическая мера ранговой корреляции (статистической зависимости рангов между двумя переменными).
Названный в честь Чарльза Спирмена, он часто обозначается греческой буквой ‘?’ (rho) и используется в основном для анализа данных.
Он измеряет силу и направление связи между двумя ранжированными переменными. Но прежде чем говорить о коэффициенте корреляции Спирмена, важно сначала понять, что такое корреляция Пирсона. Корреляция Пирсона — это статистическая мера силы линейной связи между парными данными.
Для расчета и проверки значимости ранговой переменной необходимо, чтобы следующие предположения о данных были верны:
- Интервал или уровень отношения
- Линейно связанные
- Бивариантно распределенные
Если ваши данные не удовлетворяют вышеуказанным предположениям, то вам понадобится коэффициент Спирмена. Для понимания коэффициента корреляции Спирмена необходимо знать, что такое монотонная функция. Монотонная функция — это функция, которая либо никогда не уменьшается, либо никогда не увеличивается по мере увеличения независимой переменной. Монотонную функцию можно объяснить с помощью изображения ниже:
Изображение объясняет три понятия в монотонной функции:
- Монотонно возрастающая: Когда переменная ‘x’ увеличивается, а переменная ‘y’ никогда не уменьшается.
- Монотонно убывающая: Когда переменная ‘x’ увеличивается, а переменная ‘y’ никогда не увеличивается
- Не монотонно: Когда переменная ‘x’ увеличивается, а переменная ‘y’ иногда увеличивается, а иногда уменьшается.
Монотонная зависимость является менее ограничительной по сравнению с линейной зависимостью, которая используется в коэффициенте Пирсона. Хотя монотонность не является конечным требованием для коэффициента корреляции Спирмена, не имеет смысла добиваться корреляции Спирмена без фактического определения силы и направления монотонной связи, если уже было известно, что связь между переменными немонотонна.
Узнайте больше: Анализ газона с примерами
Коэффициент корреляции Спирмена: Формула и расчет на примере

n= количество точек данных двух переменных
di = разность рангов «i-го» элемента
Коэффициент Спирмена, ?может принимать значение от +1 до -1, где,
- Значение ? равное +1 означает идеальную связь рангов
- Значение ? равное 0 означает отсутствие связи рангов
- Значение ? равное -1 означает идеальную отрицательную связь между рангами.
Чем ближе значение ? к 0, тем слабее связь между двумя рангами.
Прежде чем приступить к расчету коэффициента ранговой корреляции Спирмена, мы должны уметь ранжировать данные. Важно наблюдать, если при увеличении одной переменной другая переменная следует монотонной зависимости.
На каждом уровне необходимо сравнить значения двух переменных. Вот как происходят вычисления:
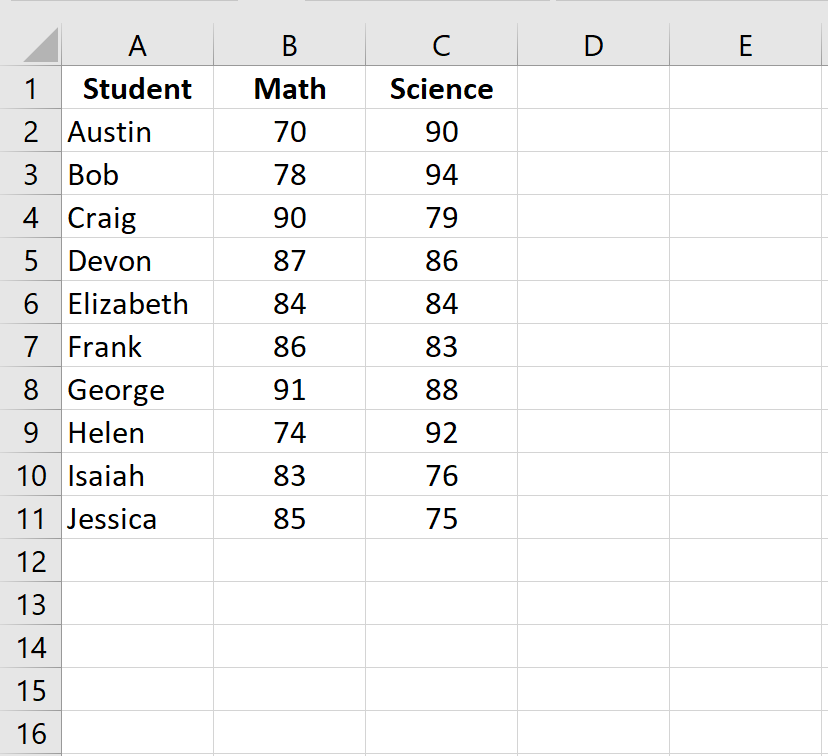
Оценки 9 учеников по истории и географии приведены в таблице ниже.
Шаг 1- Создайте таблицу полученных данных.
Шаг 2- Начните с ранжирования двух наборов данных. Ранжирование данных может быть достигнуто путем присвоения рейтинга «1» самому большому числу в столбце, «2» — второму по величине числу и так далее. Наименьшее значение обычно получает самый низкий рейтинг. Это нужно сделать для обоих наборов измерений.
Шаг 3 Добавьте к набору данных третий столбец d, d здесь обозначает разницу между рангами. Например, если ранг первого студента по физике равен 3, а по математике — 5, то разница в рангах равна 3. В четвертом столбце возведите в квадрат значения d.
| История | Ранг | География | Ранг | d | d квадрат |
| 35 | 3 | 30 | 5 | 2 | 4 |
| 23 | 5 | 33 | 3 | 2 | 4 |
| 47 | 1 | 45 | 2 | 1 | 1 |
| 17 | 6 | 23 | 6 | 0 | 0 |
| 10 | 7 | 8 | 8 | 1 | 1 |
| 43 | 2 | 49 | 1 | 1 | 1 |
| 9 | 8 | 12 | 7 | 1 | 1 |
| 6 | 9 | 4 | 9 | 0 | 0 |
| 28 | 4 | 31 | 4 | 0 | 0 |
| 12 |
Шаг 4- Сложите все ваши квадратные значения d, что составляет 12 (?d квадрат)
Шаг 5- Подставьте эти значения в формулу
=1-(6*12)/(9(81-1))
=1-72/720
=1-01
=0.9
Ранговая корреляция Спирмена для этих данных равна 0,9, и, как было сказано выше, если значение ? приближается к +1, то у них идеальная ранговая связь.
Узнайте больше: Conjoint Analysis — определение, типы, пример, алгоритм и модель
Как провести коэффициент корреляции с помощью
В этом разделе вы узнаете, как можно провести коэффициент ранговой корреляции Спирмена для вашего опроса.
Шаг 1: Перейдите в раздел Мои опросы >Выберите опрос>Аналитика
Шаг 2: Нажмите на Корреляционный анализ в разделе Анализ
Шаг 3: Нажмите на кнопку Generate Spearman Coefficient, чтобы получить подробный отчет
В приведенном выше примере коэффициент корреляции Спирмена используется для выявления связи между двумя переменными — опытом работы и ежемесячным доходом. Согласно общему представлению, ежемесячный доход должен увеличиваться с ростом опыта работы, а значит, между двумя переменными должна существовать положительная связь, что подтверждается значением rs, равным 0,97
Узнайте больше: GAP-анализ — определение, метод и шаблон с примером
From Wikipedia, the free encyclopedia
A Spearman correlation of 1 results when the two variables being compared are monotonically related, even if their relationship is not linear. This means that all data points with greater x values than that of a given data point will have greater y values as well. In contrast, this does not give a perfect Pearson correlation.
When the data are roughly elliptically distributed and there are no prominent outliers, the Spearman correlation and Pearson correlation give similar values.
The Spearman correlation is less sensitive than the Pearson correlation to strong outliers that are in the tails of both samples. That is because Spearman’s ρ limits the outlier to the value of its rank.
In statistics, Spearman’s rank correlation coefficient or Spearman’s ρ, named after Charles Spearman and often denoted by the Greek letter 

The Spearman correlation between two variables is equal to the Pearson correlation between the rank values of those two variables; while Pearson’s correlation assesses linear relationships, Spearman’s correlation assesses monotonic relationships (whether linear or not). If there are no repeated data values, a perfect Spearman correlation of +1 or −1 occurs when each of the variables is a perfect monotone function of the other.
Intuitively, the Spearman correlation between two variables will be high when observations have a similar (or identical for a correlation of 1) rank (i.e. relative position label of the observations within the variable: 1st, 2nd, 3rd, etc.) between the two variables, and low when observations have a dissimilar (or fully opposed for a correlation of −1) rank between the two variables.
Spearman’s coefficient is appropriate for both continuous and discrete ordinal variables.[1][2] Both Spearman’s 

Definition and calculation[edit]
The Spearman correlation coefficient is defined as the Pearson correlation coefficient between the rank variables.[3]
For a sample of size n, the n raw scores 


where
denotes the usual Pearson correlation coefficient, but applied to the rank variables,
is the covariance of the rank variables,
and
are the standard deviations of the rank variables.
Only if all n ranks are distinct integers, it can be computed using the popular formula
where
is the difference between the two ranks of each observation,
- n is the number of observations.
Identical values are usually[4] each assigned fractional ranks equal to the average of their positions in the ascending order of the values, which is equivalent to averaging over all possible permutations.
If ties are present in the data set, the simplified formula above yields incorrect results: Only if in both variables all ranks are distinct, then 
The first equation — normalizing by the standard deviation — may be used even when ranks are normalized to [0, 1] («relative ranks») because it is insensitive both to translation and linear scaling.
The simplified method should also not be used in cases where the data set is truncated; that is, when the Spearman’s correlation coefficient is desired for the top X records (whether by pre-change rank or post-change rank, or both), the user should use the Pearson correlation coefficient formula given above.[5]
[edit]
There are several other numerical measures that quantify the extent of statistical dependence between pairs of observations. The most common of these is the Pearson product-moment correlation coefficient, which is a similar correlation method to Spearman’s rank, that measures the “linear” relationships between the raw numbers rather than between their ranks.
An alternative name for the Spearman rank correlation is the “grade correlation”;[6] in this, the “rank” of an observation is replaced by the “grade”. In continuous distributions, the grade of an observation is, by convention, always one half less than the rank, and hence the grade and rank correlations are the same in this case. More generally, the “grade” of an observation is proportional to an estimate of the fraction of a population less than a given value, with the half-observation adjustment at observed values. Thus this corresponds to one possible treatment of tied ranks. While unusual, the term “grade correlation” is still in use.[7]
Interpretation[edit]
A positive Spearman correlation coefficient corresponds to an increasing monotonic trend between X and Y.
A negative Spearman correlation coefficient corresponds to a decreasing monotonic trend between X and Y.
The sign of the Spearman correlation indicates the direction of association between X (the independent variable) and Y (the dependent variable). If Y tends to increase when X increases, the Spearman correlation coefficient is positive. If Y tends to decrease when X increases, the Spearman correlation coefficient is negative. A Spearman correlation of zero indicates that there is no tendency for Y to either increase or decrease when X increases. The Spearman correlation increases in magnitude as X and Y become closer to being perfectly monotone functions of each other. When X and Y are perfectly monotonically related, the Spearman correlation coefficient becomes 1. A perfectly monotone increasing relationship implies that for any two pairs of data values Xi, Yi and Xj, Yj, that Xi − Xj and Yi − Yj always have the same sign. A perfectly monotone decreasing relationship implies that these differences always have opposite signs.
The Spearman correlation coefficient is often described as being «nonparametric». This can have two meanings. First, a perfect Spearman correlation results when X and Y are related by any monotonic function. Contrast this with the Pearson correlation, which only gives a perfect value when X and Y are related by a linear function. The other sense in which the Spearman correlation is nonparametric is that its exact sampling distribution can be obtained without requiring knowledge (i.e., knowing the parameters) of the joint probability distribution of X and Y.
Example[edit]
In this example, the arbitrary raw data in the table below is used to calculate the correlation between the IQ of a person with the number of hours spent in front of TV per week [fictitious values used].
IQ, 
|
Hours of TV per week, 
|
|---|---|
| 106 | 7 |
| 100 | 27 |
| 86 | 2 |
| 101 | 50 |
| 99 | 28 |
| 103 | 29 |
| 97 | 20 |
| 113 | 12 |
| 112 | 6 |
| 110 | 17 |
Firstly, evaluate 
- Sort the data by the first column (
). Create a new column
and assign it the ranked values 1, 2, 3, …, n.
- Next, sort the data by the second column (
). Create a fourth column
and similarly assign it the ranked values 1, 2, 3, …, n.
- Create a fifth column
to hold the differences between the two rank columns (
and
).
- Create one final column
to hold the value of column
squared.
IQ, 
|
Hours of TV per week, 
|
rank 
|
rank 
|

|

|
|---|---|---|---|---|---|
| 86 | 2 | 1 | 1 | 0 | 0 |
| 97 | 20 | 2 | 6 | −4 | 16 |
| 99 | 28 | 3 | 8 | −5 | 25 |
| 100 | 27 | 4 | 7 | −3 | 9 |
| 101 | 50 | 5 | 10 | −5 | 25 |
| 103 | 29 | 6 | 9 | −3 | 9 |
| 106 | 7 | 7 | 3 | 4 | 16 |
| 110 | 17 | 8 | 5 | 3 | 9 |
| 112 | 6 | 9 | 2 | 7 | 49 |
| 113 | 12 | 10 | 4 | 6 | 36 |
With 

to give
which evaluates to ρ = −29/165 = −0.175757575… with a p-value = 0.627188 (using the t-distribution).
Chart of the data presented. It can be seen that there might be a negative correlation, but that the relationship does not appear definitive.
That the value is close to zero shows that the correlation between IQ and hours spent watching TV is very low, although the negative value suggests that the longer the time spent watching television the lower the IQ. In the case of ties in the original values, this formula should not be used; instead, the Pearson correlation coefficient should be calculated on the ranks (where ties are given ranks, as described above).
Confidence intervals[edit]
Confidence intervals for Spearman’s ρ can be easily obtained using the Jackknife Euclidean likelihood approach in de Carvalho and Marques (2012).[8] The confidence interval with level 
where 


Determining significance[edit]
One approach to test whether an observed value of ρ is significantly different from zero (r will always maintain −1 ≤ r ≤ 1) is to calculate the probability that it would be greater than or equal to the observed r, given the null hypothesis, by using a permutation test. An advantage of this approach is that it automatically takes into account the number of tied data values in the sample and the way they are treated in computing the rank correlation.
Another approach parallels the use of the Fisher transformation in the case of the Pearson product-moment correlation coefficient. That is, confidence intervals and hypothesis tests relating to the population value ρ can be carried out using the Fisher transformation:
If F(r) is the Fisher transformation of r, the sample Spearman rank correlation coefficient, and n is the sample size, then
is a z-score for r, which approximately follows a standard normal distribution under the null hypothesis of statistical independence (ρ = 0).[9][10]
One can also test for significance using
which is distributed approximately as Student’s t-distribution with n − 2 degrees of freedom under the null hypothesis.[11] A justification for this result relies on a permutation argument.[12]
A generalization of the Spearman coefficient is useful in the situation where there are three or more conditions, a number of subjects are all observed in each of them, and it is predicted that the observations will have a particular order. For example, a number of subjects might each be given three trials at the same task, and it is predicted that performance will improve from trial to trial. A test of the significance of the trend between conditions in this situation was developed by E. B. Page[13] and is usually referred to as Page’s trend test for ordered alternatives.
Correspondence analysis based on Spearman’s ρ[edit]
Classic correspondence analysis is a statistical method that gives a score to every value of two nominal variables. In this way the Pearson correlation coefficient between them is maximized.
There exists an equivalent of this method, called grade correspondence analysis, which maximizes Spearman’s ρ or Kendall’s τ.[14]
Approximating Spearman’s ρ from a stream[edit]
There are two existing approaches to approximating the Spearman’s rank correlation coefficient from streaming data.[15][16] The first approach[15]
involves coarsening the joint distribution of 




these random variables. Default cutpoints are added at 



![{displaystyle M[i,j]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/46a618d7ccbbfcf5ac18e353c34883aa739e49da)
fall into the two-dimensional cell indexed by 
![{displaystyle M[i,j]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/46a618d7ccbbfcf5ac18e353c34883aa739e49da)
correlation can then be computed, based on the count matrix 
variables, no discretization procedure is necessary. This method is applicable to stationary streaming data as well as large data sets. For non-stationary streaming data, where the Spearman’s rank correlation coefficient may change over time, the same procedure can be applied, but to a moving window of observations. When using a moving window, memory requirements grow linearly with chosen window size.
The second approach to approximating the Spearman’s rank correlation coefficient from streaming data involves the use of Hermite series based estimators.[16] These estimators, based on Hermite polynomials,
allow sequential estimation of the probability density function and cumulative distribution function in univariate and bivariate cases. Bivariate Hermite series density
estimators and univariate Hermite series based cumulative distribution function estimators are plugged into a large sample version of the
Spearman’s rank correlation coefficient estimator, to give a sequential Spearman’s correlation estimator. This estimator is phrased in
terms of linear algebra operations for computational efficiency (equation (8) and algorithm 1 and 2[16]). These algorithms are only applicable to continuous random variable data, but have
certain advantages over the count matrix approach in this setting. The first advantage is improved accuracy when applied to large numbers of observations. The second advantage is that the Spearman’s rank correlation coefficient can be
computed on non-stationary streams without relying on a moving window. Instead, the Hermite series based estimator uses an exponential weighting scheme to track time-varying Spearman’s rank correlation from streaming data,
which has constant memory requirements with respect to «effective» moving window size. A software implementation of these Hermite series based algorithms exists [17] and is discussed in Software implementations.
Software implementations[edit]
- R’s statistics base-package implements the test
cor.test(x, y, method = "spearman")in its «stats» package (alsocor(x, y, method = "spearman")will work. The package spearmanCI computes confidence intervals. The package hermiter[17] computes fast batch estimates of the Spearman correlation along with sequential estimates (i.e. estimates that are updated in an online/incremental manner as new observations are incorporated). - Stata implementation:
spearman varlistcalculates all pairwise correlation coefficients for all variables in varlist. - MATLAB implementation:
[r,p] = corr(x,y,'Type','Spearman')whereris the Spearman’s rank correlation coefficient,pis the p-value, andxandyare vectors.[18] - Python has many different implementation of the spearman correlation statistic: it can be computed with the spearmanr function of the scipy.stats module, as well as with the DataFrame.corr(method=’spearman’) method from the pandas library, and the corr(x, y, method=’spearman’) function from the statistical package pingouin.
See also[edit]
- Kendall tau rank correlation coefficient
- Chebyshev’s sum inequality, rearrangement inequality (These two articles may shed light on the mathematical properties of Spearman’s ρ.)
- Distance correlation
- Polychoric correlation
References[edit]
- ^ Scale types.
- ^ Lehman, Ann (2005). Jmp For Basic Univariate And Multivariate Statistics: A Step-by-step Guide. Cary, NC: SAS Press. p. 123. ISBN 978-1-59047-576-8.
- ^ Myers, Jerome L.; Well, Arnold D. (2003). Research Design and Statistical Analysis (2nd ed.). Lawrence Erlbaum. pp. 508. ISBN 978-0-8058-4037-7.
- ^ Dodge, Yadolah (2010). The Concise Encyclopedia of Statistics. Springer-Verlag New York. p. 502. ISBN 978-0-387-31742-7.
- ^ Al Jaber, Ahmed Odeh; Elayyan, Haifaa Omar (2018). Toward Quality Assurance and Excellence in Higher Education. River Publishers. p. 284. ISBN 978-87-93609-54-9.
- ^ Yule, G. U.; Kendall, M. G. (1968) [1950]. An Introduction to the Theory of Statistics (14th ed.). Charles Griffin & Co. p. 268.
- ^ Piantadosi, J.; Howlett, P.; Boland, J. (2007). «Matching the grade correlation coefficient using a copula with maximum disorder». Journal of Industrial and Management Optimization. 3 (2): 305–312. doi:10.3934/jimo.2007.3.305.
- ^ de Carvalho, M.; Marques, F. (2012). «Jackknife Euclidean likelihood-based inference for Spearman’s rho» (PDF). North American Actuarial Journal. 16 (4): 487‒492. doi:10.1080/10920277.2012.10597644. S2CID 55046385.
- ^ Choi, S. C. (1977). «Tests of Equality of Dependent Correlation Coefficients». Biometrika. 64 (3): 645–647. doi:10.1093/biomet/64.3.645.
- ^ Fieller, E. C.; Hartley, H. O.; Pearson, E. S. (1957). «Tests for rank correlation coefficients. I». Biometrika. 44 (3–4): 470–481. CiteSeerX 10.1.1.474.9634. doi:10.1093/biomet/44.3-4.470.
- ^ Press; Vettering; Teukolsky; Flannery (1992). Numerical Recipes in C: The Art of Scientific Computing (2nd ed.). Cambridge University Press. p. 640. ISBN 9780521437202.
- ^ Kendall, M. G.; Stuart, A. (1973). «Sections 31.19, 31.21». The Advanced Theory of Statistics, Volume 2: Inference and Relationship. Griffin. ISBN 978-0-85264-215-3.
- ^ Page, E. B. (1963). «Ordered hypotheses for multiple treatments: A significance test for linear ranks». Journal of the American Statistical Association. 58 (301): 216–230. doi:10.2307/2282965. JSTOR 2282965.
- ^ Kowalczyk, T.; Pleszczyńska, E.; Ruland, F., eds. (2004). Grade Models and Methods for Data Analysis with Applications for the Analysis of Data Populations. Studies in Fuzziness and Soft Computing. Vol. 151. Berlin Heidelberg New York: Springer Verlag. ISBN 978-3-540-21120-4.
- ^ a b c Xiao, W. (2019). «Novel Online Algorithms for Nonparametric Correlations with Application to Analyze Sensor Data». 2019 IEEE International Conference on Big Data (Big Data): 404–412. doi:10.1109/BigData47090.2019.9006483. ISBN 978-1-7281-0858-2. S2CID 211298570.
- ^ a b c Stephanou, Michael; Varughese, Melvin (July 2021). «Sequential estimation of Spearman rank correlation using Hermite series estimators». Journal of Multivariate Analysis. 186: 104783. arXiv:2012.06287. doi:10.1016/j.jmva.2021.104783. S2CID 235742634.
- ^ a b Stephanou, M. and Varughese, M (2022). «hermiter: R package for Sequential Nonparametric Estimation». arXiv:2111.14091 [stat.CO].
{{cite arxiv}}: CS1 maint: multiple names: authors list (link) - ^ «Linear or rank correlation — MATLAB corr». www.mathworks.com.
Further reading[edit]
- Corder, G. W. & Foreman, D. I. (2014). Nonparametric Statistics: A Step-by-Step Approach, Wiley. ISBN 978-1118840313.
- Daniel, Wayne W. (1990). «Spearman rank correlation coefficient». Applied Nonparametric Statistics (2nd ed.). Boston: PWS-Kent. pp. 358–365. ISBN 978-0-534-91976-4.
- Spearman C. (1904). «The proof and measurement of association between two things». American Journal of Psychology. 15 (1): 72–101. doi:10.2307/1412159. JSTOR 1412159.
- Bonett D. G., Wright, T. A. (2000). «Sample size requirements for Pearson, Kendall, and Spearman correlations». Psychometrika. 65: 23–28. doi:10.1007/bf02294183. S2CID 120558581.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - Kendall M. G. (1970). Rank correlation methods (4th ed.). London: Griffin. ISBN 978-0-852-6419-96. OCLC 136868.
- Hollander M., Wolfe D. A. (1973). Nonparametric statistical methods. New York: Wiley. ISBN 978-0-471-40635-8. OCLC 520735.
- Caruso J. C., Cliff N. (1997). «Empirical size, coverage, and power of confidence intervals for Spearman’s Rho». Educational and Psychological Measurement. 57 (4): 637–654. doi:10.1177/0013164497057004009. S2CID 120481551.
External links[edit]
- Table of critical values of ρ for significance with small samples
- Spearman’s Rank Correlation Coefficient – Excel Guide: sample data and formulae for Excel, developed by the Royal Geographical Society.
17 авг. 2022 г.
читать 3 мин
В статистике корреляция относится к силе и направлению связи между двумя переменными. Значение коэффициента корреляции может варьироваться от -1 до 1 со следующими интерпретациями:
- -1: идеальная отрицательная связь между двумя переменными
- 0: нет связи между двумя переменными
- 1: идеальная положительная связь между двумя переменными
Один особый тип корреляции называется ранговой корреляцией Спирмена и используется для измерения корреляции между двумя ранжированными переменными. (например, оценка балла учащегося на экзамене по математике и оценка его оценки на экзамене по естественным наукам в классе).
В этом руководстве объясняется, как рассчитать ранговую корреляцию Спирмена между двумя переменными в Excel.
Пример: ранговая корреляция Спирмена в Excel
Выполните следующие шаги, чтобы вычислить ранговую корреляцию Спирмена между результатами экзамена по математике и результатами экзамена по естественным наукам 10 учащихся в определенном классе.
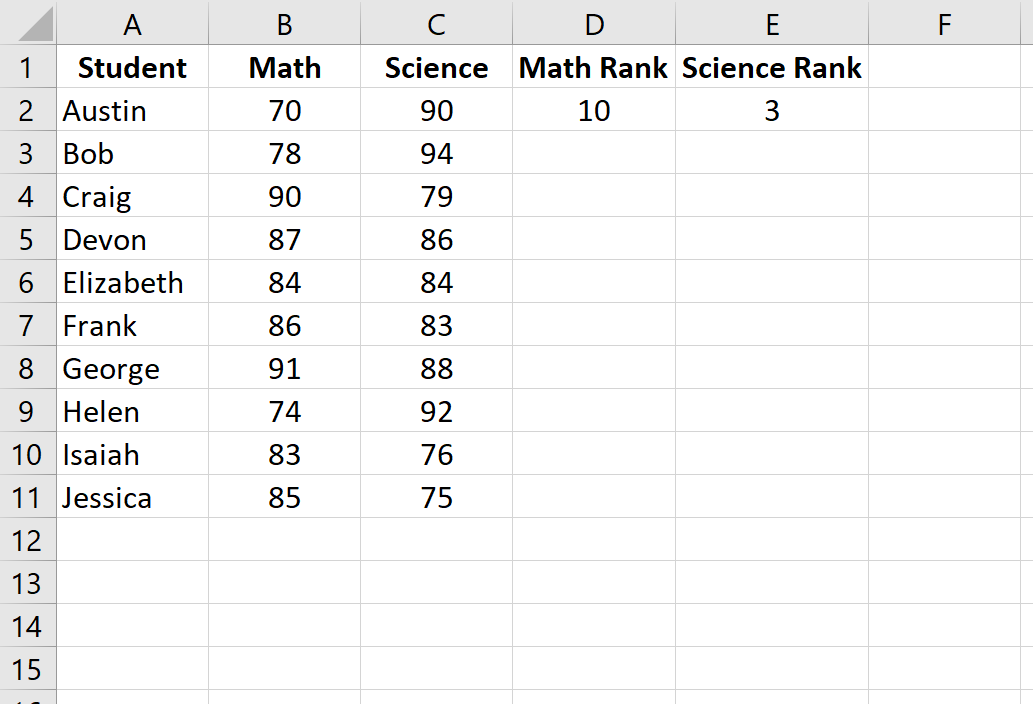
Шаг 1: Введите данные.
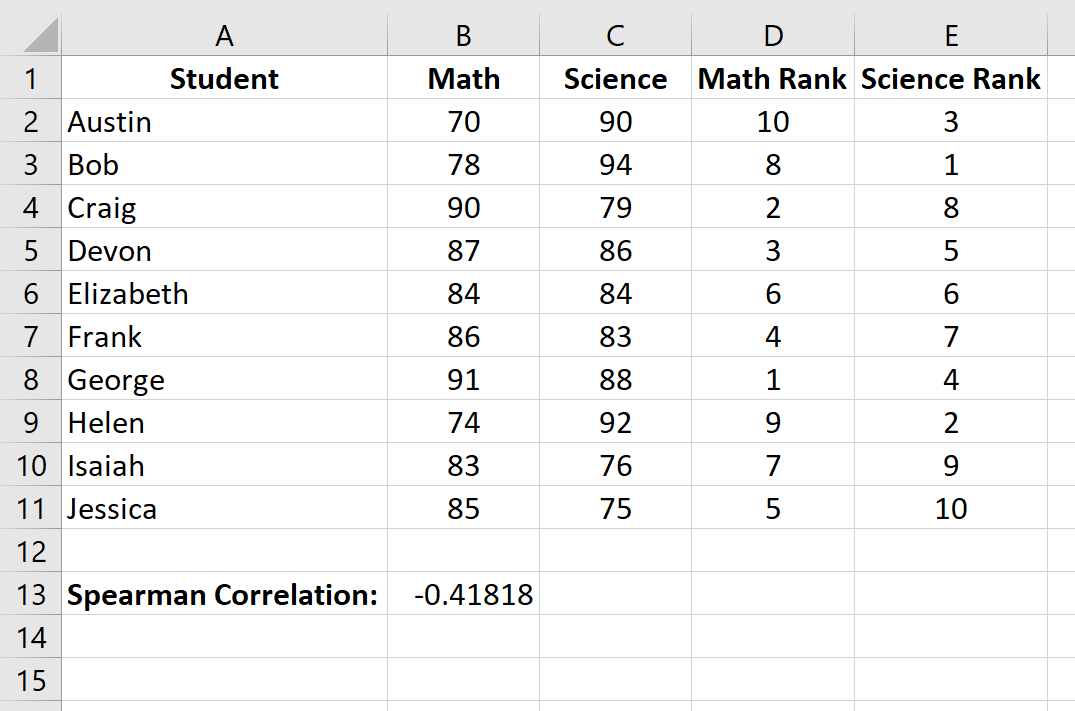
Введите экзаменационные баллы для каждого учащегося в два отдельных столбца:
Шаг 2: Рассчитайте ранги для каждого экзаменационного балла.
Далее мы рассчитаем рейтинг для каждого экзаменационного балла. Используйте следующие формулы в ячейках D2 и E2, чтобы вычислить рейтинги по математике и естественным наукам для первого ученика, Остина:
Ячейка D2: =RANK.AVG(B2, $B$2:$B$11, 0)
Ячейка E2: =RANK.AVG(C2, $C$2:$C$11, 0)
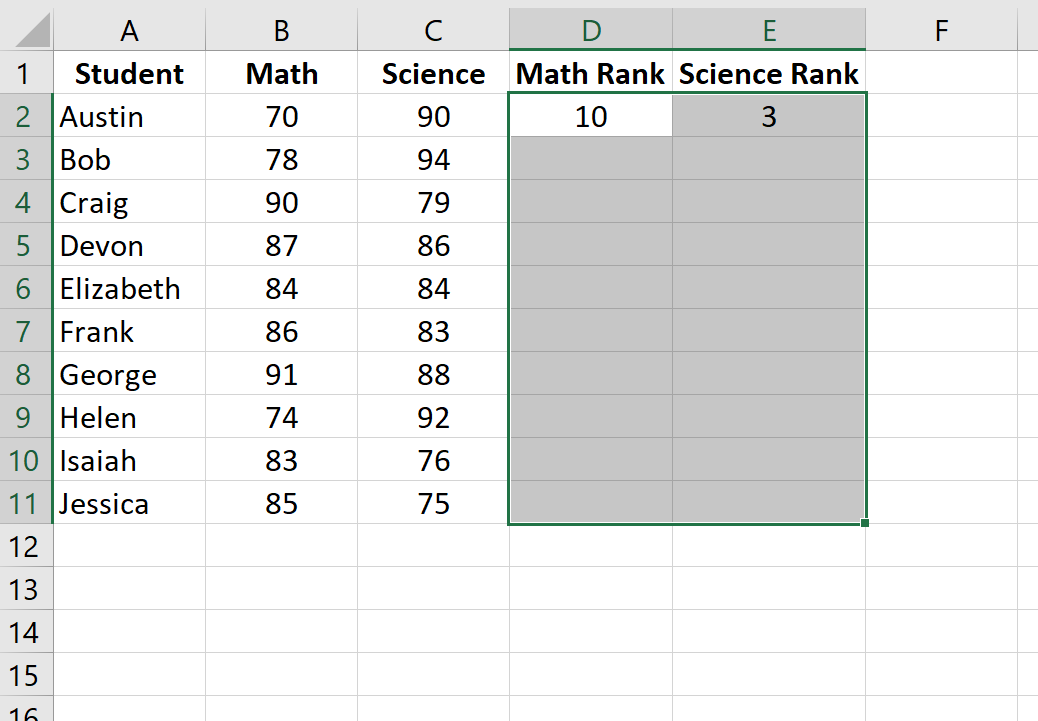
Затем выделите оставшиеся ячейки для заполнения:
Затем нажмите Ctrl+D, чтобы заполнить ранги для каждого ученика:
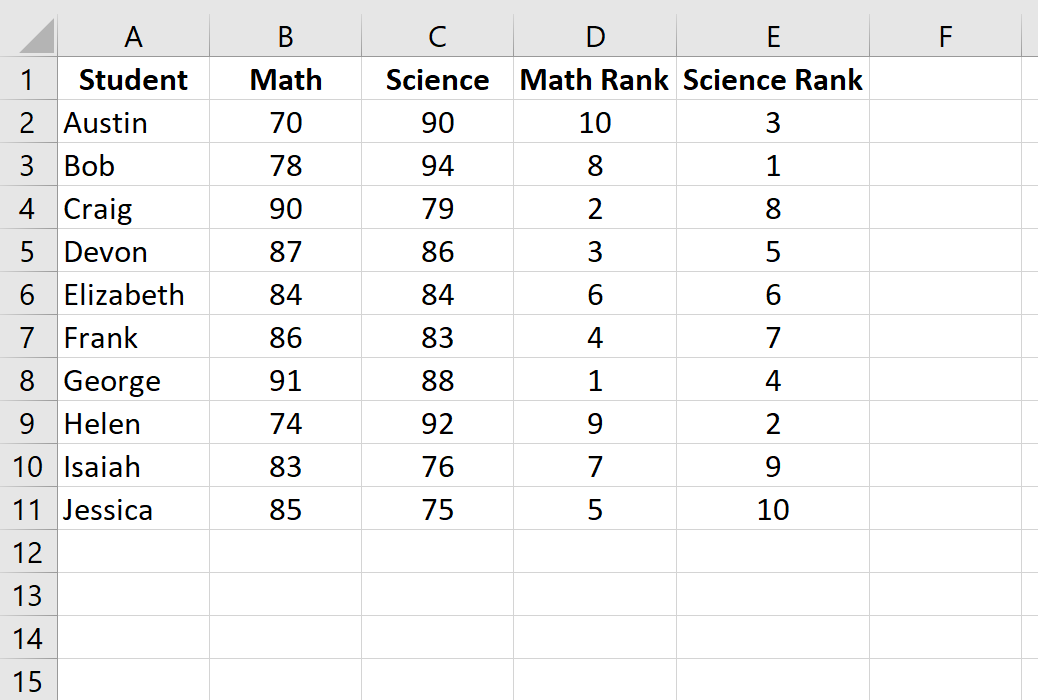
Шаг 3: Рассчитайте коэффициент ранговой корреляции Спирмена.
Наконец, мы рассчитаем коэффициент ранговой корреляции Спирмена между оценками по математике и по естественным наукам с помощью функции CORREL() :
Ранговая корреляция Спирмена оказывается равной -0,41818 .
Шаг 4 (необязательно): Определите, является ли ранговая корреляция Спирмена статистически значимой.
На предыдущем шаге мы обнаружили, что ранговая корреляция Спирмена между результатами экзаменов по математике и естественным наукам составляет -0,41818 , что указывает на отрицательную корреляцию между двумя переменными.
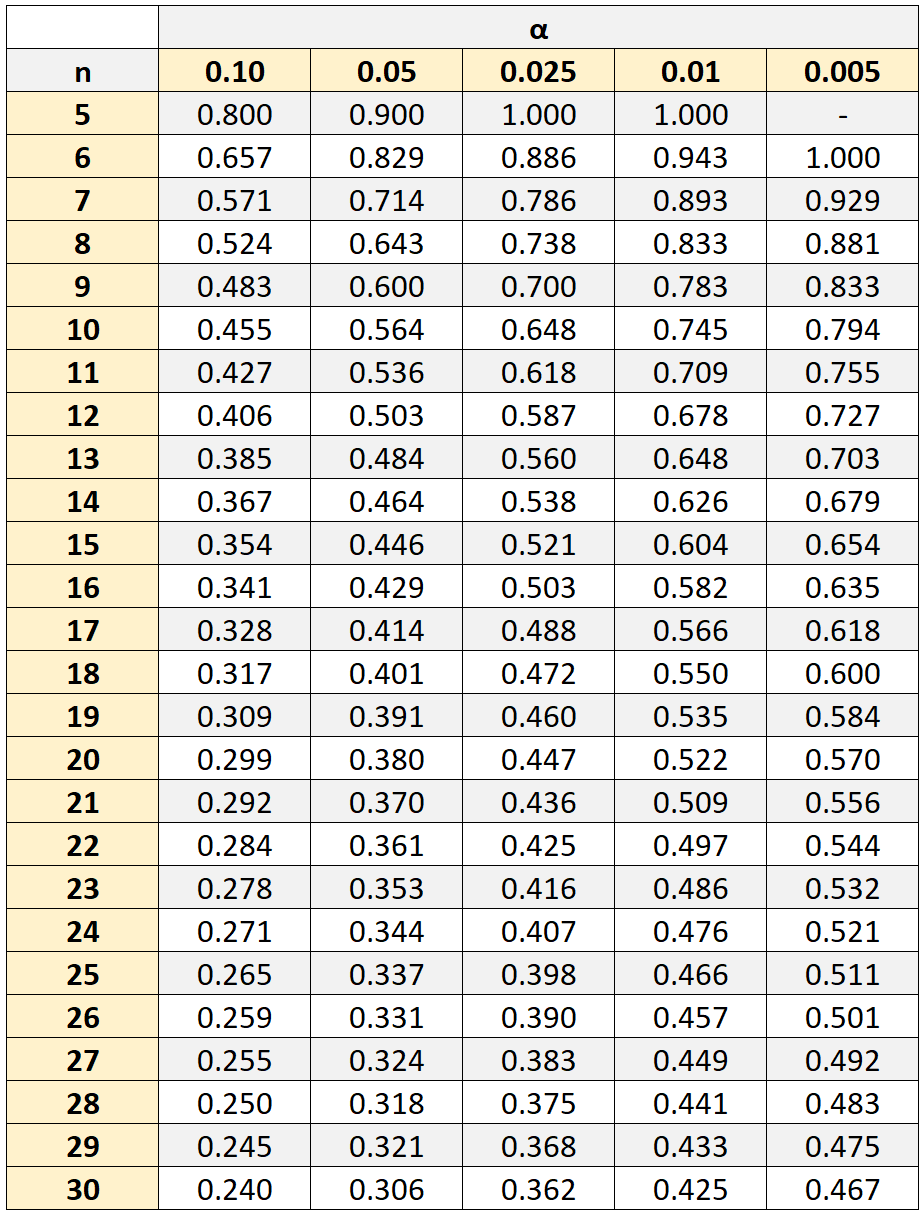
Однако, чтобы определить, является ли эта корреляция статистически значимой, нам нужно будет обратиться к таблице ранговой корреляции Спирмена критических значений, которая показывает критические значения, связанные с различными размерами выборки (n) и уровнями значимости (α).
Если абсолютное значение нашего коэффициента корреляции больше критического значения в таблице, то корреляция между двумя переменными является статистически значимой.
В нашем примере размер выборки составлял n = 10 студентов. Используя уровень значимости 0,05, мы находим, что критическое значение равно 0,564 .
Поскольку рассчитанное нами абсолютное значение рангового коэффициента корреляции Спирмена ( 0,41818 ) не превышает этого критического значения, это означает, что корреляция между баллами по математике и естественным наукам не является статистически значимой.
Назначение
рангового коэффициента корреляции
Метод
ранговой корреляции Спирмена позволяет
определить тесноту (силу) и направление
корреляционной связи между двумя
признаками или
двумя
профилями {иерархиями) признаков.
Описание метода
Для подсчета
ранговой корреляции необходимо
располагать двумя рядами значений,
которые могут быть проранжированы.
Такими рядами значений могут быть:
1) два
признака, измеренные
в одной и той же группе испытуемых;
2) две
индивидуальные иерархии признаков,
выявленные
у двух испытуемых по одному и тому
же набору признаков (например, личностные
профили по 16-факторному опроснику Р. Б.
Кеттелла, иерархии ценностей по методике
Р. Рокича, последовательности предпочтений
в выборе из нескольких альтернатив и
др.);
3) две
групповые иерархии признаков;
4)
индивидуальная
и групповая иерархии
признаков.
Вначале показатели
ранжируются отдельно по каждому из
признаков. Как правило, меньшему значению
признака начисляется меньший ранг.
Рассмотрим
случай 1 (два признака). Здесь
ранжируются индивидуальные значения
по первому признаку, полученные разными
испытуемыми, а затем индивидуальные
значения по второму признаку.
Если
два признака связаны положительно, то
испытуемые, имеющие низкие ранги по
одному из них, будут иметь низкие ранги
и по другому, а испытуемые, имеющие
высокие ранги по одному из признаков,
будут иметь по другому признаку также
высокие ранги. Для подсчета rs
необходимо
определить разности (d)
между рангами, полученными данным
испытуемым по обоим признакам. Затем
эти показатели d
определенным образом преобразуются и
вычитаются из 1. Чем меньше разности
между рангами, тем больше будет rs,
тем ближе он будет к +1.
Если
корреляция отсутствует, то все ранги
будут перемешаны и между ними не будет
никакого соответствия. Формула составлена
так, что в
этом
случае rs,
окажется близким к 0.
В случае отрицательной
корреляции низким рангам испытуемых
по одному признаку будут соответствовать
высокие ранги по другому признаку, и
наоборот.
Чем
больше несовпадение между рангами
испытуемых по двумя переменным, тем
ближе rs
к -1.
Рассмотрим
случай 2 (два индивидуальных профиля).
Здесь
ранжируются индивидуальные значения,
полученные каждым из 2-х испытуемым по
определенному (одинаковому для них
обоих) набору признаков. Первый ранг
получит признак с самым низким значением;
второй ранг — признак с более высоким
значением и т.д. Очевидно, что все признаки
должны быть измерены в одних и тех же
единицах, иначе ранжирование невозможно.
Например, невозможно проранжировать
показатели по личностному опроснику
Кеттелла (16PF),
если они выражены в «сырых»
баллах, поскольку по разным факторам
диапазоны значений различны: от 0 до 13,
от 0 до 20 и от 0 до 26. Мы не можем сказать,
какой из факторов будет занимать первое
место по выраженности, пока не приведем
все значения к единой шкале (чаще всего
это шкала стенов).
Если
индивидуальные иерархии двух испытуемых
связаны положительно, то признаки,
имеющие низкие ранги у одного из них,
будут иметь низкие ранги и у другого, и
наоборот. Например, если у одного
испытуемого фактор Е (доминантность)
имеет самый низкий ранг, то и
у
другого испытуемого он должен иметь
низкий ранг, если у одного испытуемого
фактор С (эмоциональная устойчивость)
имеет высший ранг, то и другой испытуемый
должен иметь по этому фактору высокий
ранг и т.д.
Рассмотрим
случай 3 (два групповых профиля). Здесь
ранжируются среднегрупповые значения,
полученные в 2-х группах испытуемых
по определенному, одинаковому для двух
групп, набору признаков. В дальнейшем
линия рассуждений такая же, как и в
предыдущих двух случаях.
Рассмотрим
случай 4 (индивидуальный и групповой
профили). Здесь
ранжируются отдельно индивидуальные
значения испытуемого и
среднегрупповые
значения по тому же набору признаков,
которые получены, как правило, при
исключении этого отдельного испытуемого
— он не участвует в среднегрупповом
профиле, с которым будет сопоставляться
его индивидуальный профиль. Ранговая
корреляция позволит проверить, насколько
согласованы индивидуальный и групповой
профили.
Во
всех четырех случаях значимость
полученного коэффициента корреляции
определяется по количеству ранжированных
значений N.
В
первом случае это количество будет
совпадать с объемом выборки п. Во втором
случае количеством наблюдений будет
количество признаков, составляющих
иерархию. В третьем и четвертом случае
N
— это
также количество сопоставляемых
признаков, а не количество испытуемых
в группах. Подробные пояснения даны в
примерах.
Если
абсолютная величина rs
достигает критического значения или
превышает его, корреляция достоверна.
Гипотезы
Возможны два
варианта гипотез. Первый относится к
случаю 1, второй — к трем остальным
случаям.
Первый вариант
гипотез
H0:
Корреляция
между переменными А и Б не отличается
от нуля.
H1:
Корреляция между переменными А и Б
достоверно отличается от нуля.
Второй вариант
гипотез
H0:
Корреляция
между иерархиями А и Б не отличается от
нуля.
H1:
Корреляция
между иерархиями А и Б достоверно
отличается от нуля.
Графическое
представление метода ранговой корреляции
Чаще всего
корреляционную связь представляют
графически в виде облака точек или в
виде линий, отражающих общую тенденцию
размещения точек в пространстве двух
осей: оси признака А и признака Б (см.
Рис. 6.2).
Попробуем
изобразить ранговую корреляцию в виде
двух рядов ранжированных значений,
которые попарно соединены линиями (Рис.
6.3). Если ранги по признаку А и по признаку
Б совпадают, то между ними оказывается
горизонтальная линия, если ранги не
совпадают, то линия становится наклонной.
Чем больше несовпадение рангов, тем
более наклонной становится линия.
Слева на Рис. 6.3 отображена максимально
высокая положительная корреляция
(rв=+1,0)
— практически это «лестница». В
центре отображена нулевая корреляция
— плетенка с неправильными переплетениями.
Все ранги здесь перепутаны. Справа
отображена максимально высокая
отрицательная корреляция (rs=-1,0)
-паутина с правильным переплетением
линий.
Рис. 6.3. Графическое
представление ранговой корреляции:
а) высокая
положительная корреляция;
б) нулевая корреляция;
в) высокая
отрицательная корреляция
Ограничения
коэффициента
ранговой корреляции
1. По
каждой переменной должно быть представлено
не менее 5 наблюдений. Верхняя граница
выборки определяется имеющимися
таблицами критических значений
(Табл.XVI
Приложения 1), а именно N≤40.
2.
Коэффициент ранговой корреляции Спирмена
rs
при большом количестве одинаковых
рангов по одной или обеим сопоставляемым
переменным дает огрубленные значения.
В идеале оба коррелируемых ряда должны
представлять собой две последовательности
несовпадающих значений. В случае,
если это условие не соблюдается,
необходимо вносить поправку на
одинаковые ранги. Соответствующая
формула дана в примере 4.
Пример
1 — корреляция между
двумя признаками
В
исследовании,
моделирующем деятельность авиадиспетчера
(Одерышев Б.С., Шамова Е.П., Сидоренко
Е.В., Ларченко Н.Н., 1978), группа испытуемых,
студентов физического факультета ЛГУ
проходила подготовку перед началом
работы на тренажере. Испытуемые
должны были решать задачи по выбору
оптимального типа взлетно-посадочной
полосы для заданного типа самолета.
Связано ли количество ошибок,
допущенных испытуемыми в тренировочной
сессии, с показателями вербального и
невербального интеллекта, измеренными
по методике Д. Векслера?
Таблица 6.1
Показатели
количества ошибок в тренировочной
сессии и показатели уровня вербального
и невербального интеллекта у
студентов-физиков (N=10)
|
Испытуемый |
Количество ошибок |
Показатель вербального интеллекта |
Показатель невербального интеллекта |
|
|
1 |
Т.А. |
29 |
131 |
106 |
|
2 |
П.А. |
54 |
132 |
90 |
|
3 |
Ч.И. |
13 |
121 |
95 |
|
4 |
Ц.А. |
8 |
127 |
116 |
|
5 |
См.А. |
14 |
136 |
. 127 |
|
6 |
К.Е. |
26 |
124 |
107 |
|
7 |
К.А. |
9 |
134 |
104 |
|
8 |
Б.Л. |
20 |
136 |
102 |
|
9 |
И.А. |
2 |
132 |
111 |
|
10 |
Ф.В. |
17 |
136 |
99 |
|
Суммы |
192 |
1309 |
1057 |
|
|
Средние |
19,2 |
130,9 |
105,7 |
Сначала попробуем
ответить на вопрос, связаны ли между
собой показатели количества ошибок и
вербального интеллекта.
Сформулируем
гипотезы.
H0:
Корреляция
между показателем количества ошибок в
тренировочной сессии и уровнем вербального
интеллекта не отличается от нуля.
H1:
Корреляция
между показателем количества ошибок в
тренировочной сессии и уровнем вербального
интеллекта статистически значимо
отличается от нуля.
Далее нам необходимо
проранжировать оба показателя, Приписывая
меньшему значению меньший ранг, затем
подсчитать разности между рангами,
которые получил каждый испытуемый по
двум переменным (признакам), и возвести
эти разности в квадрат. Произведем все
необходимые расчеты в таблице.
В Табл.
6.2 в первой колонке слева представлены
значения по показателю количества
ошибок; в следующей колонке — их ранги.
В третьей колонке слева представлены
значения по показателю вербального
интеллекта; в следующем столбце — их
ранги. В пятом слева представлены
разности d
между
рангом по переменной А (количество
ошибок) и переменной Б (вербальный
интеллект). В последнем столбце
представлены квадраты разностей — d2.
Таблица 6.2
Расчет
d2
для
рангового коэффициента корреляции
Спирмена rs
при сопоставлении показателей количества
ошибок и вербального интеллекта у
студентов-физиков (N=10)
|
Испытуемый |
Переменная А количество ошибок |
Переменная Б вербальный интеллект. |
d — ранг Б) |
J2 |
|||
|
Индивидуальные значения |
Ранг |
Индивидуальные значения |
Ранг |
||||
|
1 |
ТА. |
29 |
9 |
131 |
4 |
5 |
25 |
|
2 |
ПА. |
54 |
10 |
132 |
5.5 |
4,5 |
20.25 |
|
3 |
Ч.И. |
13 |
4 |
121 |
1 |
3 |
9 |
|
4 |
Ц.А. |
8 |
2 |
127 |
3 |
-1 |
1 |
|
5 |
См.А. |
14 |
5 |
136 |
9 |
-4 |
16 |
|
6 |
К.Е. |
26 |
8 |
124 |
2 |
6 |
36 |
|
7 |
К.А. |
9 |
3 |
134 |
7 |
-4 |
16 |
|
8 |
Б.Л. |
20 |
7 |
136 |
9 |
-2 |
4 |
|
9 |
И.А. |
2 |
1 |
132 |
5,5 |
-4,5 |
20,25 |
|
10 |
Ф.В. |
17 |
6 |
136 |
9 |
9 |
|
|
Суммы |
55 |
55 |
0 |
156,5 |
Коэффициент
ранговой корреляции Спирмена подсчитывается
по формуле:
где d
— разность
между рангами по двум переменным для
каждого испытуемого;
N —
количество
ранжируемых значений, в. данном случае
количество испытуемых.
Рассчитаем
эмпирическое значение rs:
Полученное
эмпирическое значение гs
близко к 0. И все же определим критические
значения rs
при N=10
по Табл. XVI
Приложения 1:

Ответ:
H0
принимается.
Корреляция между показателем количества
ошибок в тренировочной сессии и уровнем
вербального интеллекта не отличается
от нуля.
Теперь попробуем
ответить на вопрос, связаны ли между
собой показатели количества ошибок и
невербального интеллекта.
Сформулируем
гипотезы.
H0:
Корреляция
между показателем количества ошибок в
тренировочной сессии и уровнем
невербального интеллекта не отличается
от 0.
H1:
Корреляция между показателем количества
ошибок в тренировочной сессии и уровнем
невербального интеллекта статистически
значимо отличается от 0.
Результаты
ранжирования и сопоставления рангов
представлены в Табл. 6.3.
Таблица 6.3
Расчет
d2
для
рангового коэффициента корреляции
Спирмена rs
при сопоставлении показателей количества
ошибок и невербального интеллекта у
студентов-физиков (N=10)
|
Испытуемый |
Переменная
количество |
Переменная ;
невербальный |
d
— ранг |
d2 |
|||
|
Индивидуальные |
Ранг |
Индивидуальные |
Ранг |
||||
|
значения |
значения |
||||||
|
1 |
Т.А. |
29 |
9 |
106 |
6 |
3 |
9 |
|
2 |
П:А. |
54 |
10 |
90 |
1 |
9 |
81 |
|
3 |
Ч.И. |
13 |
4 |
95 |
2 |
2 |
4 |
|
4 |
Ц-А. „ |
8 |
2 |
116 |
9 |
-7 |
49 |
|
5 |
См.А. |
14 |
5 |
127 |
10 |
-5 |
25 |
|
6 |
К.Е. |
26 |
8 |
107 |
7 |
1 |
1 |
|
7 |
К.А. |
9 |
3 |
104 |
5 |
-2 |
4 |
|
8 |
Б.Л. |
20 |
7 |
102 |
4 |
3 |
9 |
|
9 |
И.А. |
2 |
1 |
111 |
8 |
-7 |
49 |
|
10 |
Ф.В. |
17 |
6 |
99 |
3 |
3 |
9 |
|
Суммы |
55 |
55 |
0 |
240 |
Мы
помним, что для определения значимости
rs
неважно, является ли он положительным
или отрицательным, важна лишь его
абсолютная величина. В данном случае:
rs
эмп<rs
ко.
Ответ:
H0
принимается. Корреляция между показателем
количества ошибок в тренировочной
сессии и уровнем невербального интеллекта
случайна, rs
не отличается от 0.
Вместе
с тем, мы можем обратить внимание на
определенную тенденцию отрицательной
связи
между этими двумя переменными. Возможно,
мы смогли бы ее подтвердить на статистически
значимом уровне, если бы увеличили объем
выборки.
Пример 2 — корреляция
между индивидуальными профилями
В исследовании,
посвященном проблемам ценностной
реориента-ции, выявлялись иерархии
терминальных ценностей по методике М.
Рокича у родителей и их взрослых детей
(Сидоренко Е.В., 1996). Ранги терминальных
ценностей, полученные при обследовании
пары мать-дочь (матери — 66 лет, дочери —
42 года) представлены в Табл. 6.4. Попытаемся
определить, как эти ценностные иерархии
коррелируют друг с другом.
Таблица 6.4
Ранги терминальных
ценностей по списку М.Рокича в
индивидуальных иерархиях матери и
дочери
|
Ряд1: |
Ряд 2: |
|||
|
Терминальные ценности |
Ранг ценностей в |
Ранг ценностей в |
d |
d2 |
|
иерархии матери |
иерархии дочери |
|||
|
1 Активная деятельная жизнь |
15 |
15 |
0 |
0 |
|
2 Жизненная |
1 |
3 |
-2 |
4 |
|
3 Здоровье |
7 |
14 |
-7 |
49 |
|
4 Интересная |
8 |
12 |
-4 |
16 |
|
5 Красота |
16 |
17 |
-1 |
1 |
|
6 Любовь |
11 |
10 |
1 |
1 |
|
7 Материально |
12 |
13 |
-1 |
1 |
|
8 Наличие хороших и |
9 |
11 |
-2 |
4 |
|
9 Общественное |
17 |
5 |
12 |
144 |
|
10 Познание |
5 |
1 |
4 |
16 |
|
11 Продуктивная |
2 |
2 |
0 |
0 |
|
12 Развитие |
6 |
8 |
-2 |
4 |
|
13 Развлечения |
18 |
18 |
0 |
0 |
|
14 Свобода |
4 |
6 |
-2 |
4 |
|
15 Счастливая семейная жизнь |
13 |
4 |
9 |
81 |
|
16 Счастье |
14 |
16 |
-2 |
4 |
|
17 Творчество |
10 |
9 |
1 |
1 |
|
18 Уверенность |
3 |
7 |
-4 |
16 |
|
Суммы |
171 |
171 |
0 |
346 |
Сформулируем
гипотезы.
H0:
Корреляция
между иерархиями терминальных ценностей
матери и дочери не отличается от нуля.
H1:
Корреляция между иерархиями терминальных
ценностей матери и дочери статистически
значимо отличается от нуля.
Поскольку
ранжирование ценностей предполагается
самой процедурой исследования, нам
остается лишь подсчитать разности между
рангами 18 ценностей в двух иерархиях .
В 3-м и 4-м столбцах Табл. 6.4 представлены
разности d
и
квадраты этих разностей d2.
Определяем
эмпирическое значение rs
по формуле:
где d
—
разности между рангами по каждой из
переменных, в данном случае по каждой
из терминальных ценностей;
N —
количество переменных, образующих
иерархию, в данном случае количество
ценностей.
Для данного примера:
По
Табл. XVI
Приложения 1 определяем критические
значения:
Ответ:
H0
отвергается.
Принимается H1.
Корреляция между иерархиями терминальных
ценностей матери и дочери статистически
значима (р<0,01) и является положительной.
По данным Табл.
6.4 мы можем определить, что основные
расхождения приходятся на ценности
«Счастливая семейная жизнь»,
«Общественное признание» и
«Здоровье», ранги остальных ценностей
достаточно близки.
Пример 3 — корреляция
между двумя групповыми иерархиями
Джозеф
Вольпе в книге, написанной совместно с
сыном (Wolpe
J.,
Wolpe
D.,
1981) приводит упорядоченный перечень из
наиболее часто встречающихся у
современного человека «бесполезных»,
по его обозначению, страхов, которые
не несут сигнального значения и лишь
мешают полноценно жить и действовать.
В отечественном исследовании, проведенном
М.Э. Раховой (1994) 32 испытуемых должны
были по 10-балльной шкале оценить,
насколько актуальным для них является
тот или иной вид страха из перечня
Вольпе3.
Обследованная выборка состояла из
студентов Гидрометеорологического и
Педагогического институтов
Санкт-Петербурга: 15 юношей и 17 девушек
в возрасте от 17 до 28 лет, средний возраст
23 года.
Данные, полученные
по 10-балльной шкале, были усреднены по
32 испытуемым, и средние проранжированы.
В Табл. 6.5 представлены ранговые
показатели, полученные Дж. Вольпе и М.
Э. Раховой. Совпадают ли ранговые
последовательности 20 видов страха?
Сформулируем
гипотезы.
H0:
Корреляция
между упорядоченными перечнями видов
страха в американской и отечественных
выборках не отличается от нуля.
H1:
Корреляция между упорядоченными
перечнями видов страха в американской
и отечественной выборках статистически
значимо отличается от нуля.
Все расчеты,
связанные с вычислением и возведением
в квадрат разностей между рангами разных
видов страха в двух выборках, представлены
в Табл. 6.5.
Таблица 6.5
Расчет
d
для
рангового коэффициента корреляции
Спирмена при сопоставлении упорядоченных
перечней видов страха в американской
и отечественной выборках
|
Виды страха |
Ранг в американской выборке |
Ранг в российской выборке |
d |
d2 |
|
|
1 |
Страх |
1 |
7 |
-6 |
36 |
|
2 |
Страх |
2 |
12 |
-10 |
100 |
|
3 |
Страх |
3 |
10 |
-7 |
49 |
|
4 |
Страх |
4 |
6 |
-2 |
4 |
|
5 |
Страх |
5 |
9 |
-4 |
16 |
|
6 |
Страх |
6 |
2 |
4 |
16 |
|
7 |
Страх |
7 |
5 |
2 |
4 |
|
8 |
Страх |
8 |
1 |
7 |
49 |
|
9 |
Страх |
9 |
16 |
-7 |
49 |
|
10 |
Страх |
10 |
13 |
-3 |
9 |
|
И |
Страх |
11 |
3 |
8 |
64 |
|
12 |
Страх |
12 |
19 |
-7 |
49 |
|
13 |
Страх |
13 |
20 |
-7 |
49 |
|
14 |
Страх |
14 |
17 |
-3 |
9 |
|
15 |
Страх |
15 |
4 |
11 |
121 |
|
16 |
Страх |
16 |
11 |
5 |
25 |
|
17 |
Страх |
17 |
18 |
-1 |
1 |
|
18 |
Страх |
18 |
8 |
10 |
100 |
|
19 |
Страх |
19 |
15 |
4 |
16 |
|
20 |
Страх |
20 |
14 |
6 |
36 |
|
Суммы |
210 |
210 |
0 |
802 |
Определяем
эмпирическое значение
rs:
По
Табл. XVI
Приложения 1 определяем критические
значения гs
при N=20:
Ответ:
H0
принимается. Корреляция между
упорядоченными перечнями видов страха
в американской и отечественной выборках
не достигает уровня статистической
значимости, т. е. значимо не отличается
от нуля.
Пример
4 — корреляция между индивидуальным и
среднегрупповым профилями
Выборке
петербуржцев в возрасте от 20
до
78
лет
(31
мужчина, 46 женщин),
уравновешенной по возрасту таким
образом, что лица в возрасте старше 55
лет составляли в
ней
50%4,
предлагалось ответить на вопрос: «Какой
уровень развития каждого из перечисленных
ниже качеств необходим для депутата
Городского собрания Санкт-Петербурга?»
(Сидоренко Е.В., Дерманова И.Б., Анисимова
О.М., Витенберг Е.В., Шульга А.П., 1994).
Оценка
производилась по 10-балльной шкале.
Параллельно с этим обследовалась выборка
из депутатов и кандидатов в депутаты
в Городское собрание Санкт-Петербурга
(n=14).
Индивидуальная диагностика политических
деятелей и претендентов производилась
с помощью Оксфордской системы
экспресс-видеодиагностики по тому же
набору личностных качеств, который
предъявлялся выборке избирателей.
В Табл.
6.6 представлены средние значения,
полученные для каждого из качеств в
выборке
избирателей («эталонный ряд») и
индивидуальные значения одного из
депутатов Городского собрания.
Попытаемся
определить, насколько индивидуальный
профиль депутата К-ва коррелирует с
эталонным профилем.
Таблица 6.6
Усредненные
эталонные оценки избирателей (п=77) и
индивидуальные показатели депутата
К-ва по 18 личностным качествам
экспресс-видеодиагностики
|
Наименование качества |
Усредненные эталонные |
Индивидуальные показатели депутата |
|
1. Общий уровень культуры |
8,64 |
15 |
|
2. Обучаемость |
7,89 |
7 |
|
3. Логика |
8,38 |
12 |
|
4. Способность к творчеству нового |
6,97 |
5 |
|
5.. Самокритичность |
8,28 |
14 |
|
6. Ответственность |
9,56 |
18 |
|
7. Самостоятельность |
8,12 |
13 |
|
8. Энергия, активность |
8,41 |
17 |
|
9. Целеустремленность |
8,00 |
19 |
|
10. Выдержка, самообладание |
8,71 |
9 |
|
И. Стойкость |
7,74 |
16 |
|
12. Личностная зрелость |
8,10 |
11 |
|
13. Порядочность |
9,02 |
12 |
|
14. Гуманизм |
7.89 |
10 |
|
15. Умение общаться с людьми |
8,74 |
8 |
|
16. Терпимость к чужому мнению |
7.84 |
6 |
|
17. Гибкость поведения |
7,67 |
4 |
|
18. Способность производить благоприятное |
7,23 |
8 |
Таблица 6.7
Расчет
d2
для
рангового коэффициента корреляции
Спирмена между эталонным и индивидуальным
профилями личностных качеств депутата
|
Наименование качества |
Ряд 1: ранг качества в эталонном профиле |
Ряд 2: ранг качества в индивидуальном |
d |
d2 |
|
1 Ответственность |
1 |
2 |
-1 |
1 |
|
2 Порядочность |
2 |
8,5 |
-6,5 |
42,25 |
|
3 Умение общаться с людьми |
3 |
13,5 |
-10,5 |
110,25 |
|
4 Выдержка, самообладание |
4 |
12 |
-8 |
64 |
|
5 Общий уровень культуры |
5 |
5 |
0 |
0 |
|
6 Энергия, активность |
6 |
3 |
3 |
9 |
|
7 Логика |
7 |
8,5 |
-1,5 |
2,25 |
|
8 Самокритичность |
8 |
6 |
2 |
4 |
|
9 Самостоятельность |
9 |
7 |
2 |
4 |
|
10 Личностная зрелость |
10 |
10 |
0 |
0 |
|
И Целеустремленность |
И |
1 |
10 |
100 |
|
12 Обучаемость |
12,5 |
15 |
-2,5 |
6,25 |
|
13 Гуманизм |
12,5 |
И |
1,5 |
2,25 |
|
14 Терпимость к чужому мнению |
14 |
16 |
-2 |
4 |
|
15 Стойкость |
15 |
4 |
11 |
121 |
|
16 Гибкость поведения |
16 |
18 |
-2 |
4 |
|
17 Способность производить благоприятное |
17 |
13,5 |
3,5 |
12,25 |
|
18 Способность к творчеству нового |
18. |
17 |
1 |
1 |
|
Суммы |
171 |
171 |
0 |
487,5 |
Как
видно из Табл. 6.6, оценки избирателей и
индивидуальные показатели депутата
варьируют в разных диапазонах.
Действительно оценки избирателей были
получены по 10-балльной шкале, а
индивидуальные показатели по
экспресс-видеодиагностике измеряются
по 20-ти балльной шкале. Ранжирование
позволяет нам перевести обе шкалы
измерения в единую шкалу, где единицей
измерения будет 1 ранг, а максимальное
значение составит 18 рангов.
Ранжирование, как
мы помним, необходимо произвести отдельно
по каждому ряду значений. В данном случае
целесообразно начислять большему
значению меньший ранг, чтобы сразу можно
было увидеть, на каком месте по значимости
(для избирателей) или по выраженности
(у депутата) находится то или иное
качество.
Результаты
ранжирования представлены в Табл. 6.7.
Качества перечислены в последовательности,
отражающей эталонный профиль.
Сформулируем
гипотезы.
H0:
Корреляция между индивидуальным профилем
депутата К-ва и эталонным профилем,
построенным по оценкам избирателей, не
отличается от нуля.
H1:
Корреляция между индивидуальным профилем
депутата К-ва и эталонным профилем,
построенным по оценкам избирателей,
статистически значимо отличается
от нуля. Поскольку в обоих сопоставляемых
ранговых рядах присутствуют
группы одинаковых
рангов, перед подсчетом коэффициента
ранговой
корреляции
необходимо внести поправки на одинаковые
ранги Та
и Тb:
где а
— объем
каждой группы одинаковых рангов в
ранговом ряду А,
b
— объем
каждой группы одинаковых рангов в
ранговом ряду В.
В
данном случае, в ряду А (эталонный
профиль) присутствует одна группа
одинаковых рангов — качества «обучаемость»
и «гуманизм» имеют один и тот же
ранг 12,5; следовательно, а=2.
Tа=(23-2)/12=0,50.
В ряду
В (индивидуальный профиль) присутствует
две группы одинаковых рангов, при этом
b1=2
и
b2=2.
Ta=[(23-2)+(23-2)]/12=1,00
Для
подсчета эмпирического значения rs
используем формулу
В данном случае:
Заметим,
что если бы поправка на одинаковые ранги
нами не вносилась, то величина rs
была бы лишь на (на 0,0002) выше:
При
больших количествах одинаковых рангов
изменения г5
могут оказаться гораздо более
существенными. Наличие одинаковых
рангов означает меньшую степень
дифференцированное™ упорядоченных
переменных и, следовательно, меньшую
возможность оценить степень связи между
ними (Суходольский Г.В., 1972, с.76).
По
Табл. XVI
Приложения 1 определяем критические
значения г, при N=18:
Ответ:
Hq
отвергается.
Корреляция между индивидуальным профилем
депутата К-ва и эталонным профилем,
отвечающим требованиям избирателей,
статистически значима (р<0,05) и является
положительной.
Из
Табл. 6.7 видно, что депутат К-в имеет
более низкий ранг по шкалам Умения
общаться с людьми и более высокие ранги
по шкалам Целеустремленности и Стойкости,
чем это предписывается избирательским
эталоном. Этими расхождениями, главным
образом, и объясняется некоторое снижение
полученного rs.
Сформулируем
общий алгоритм подсчета rs.