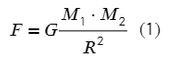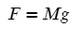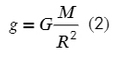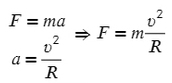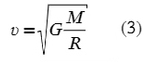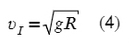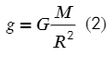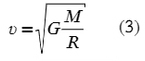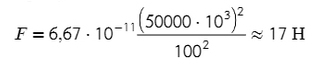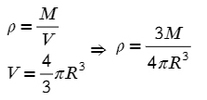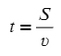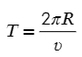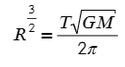Как найти радиус зная ускорение свободного падения

Движение спутников

Ускорение свободного падения

Первая космическая скорость

Вторая космическая скорость

«Звездная» болезнь — дело опасное, но излечимое. Начинать советую с этой статьи.

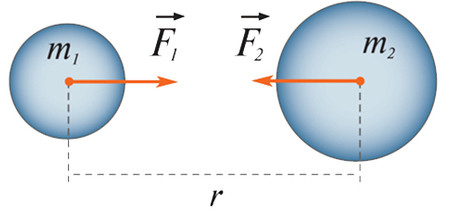
Еще в 17 веке Ньютон открыл закон всемирного тяготения, а в 21 веке кто-то еще верит, что Земля плоская.

Каждый пусть решит сам для себя, какая же на самом деле Земля, а я по старинке буду думать, что она круглая.

По закону всемирного тяготения сила притяжения двух тел:

G = 6,67×10⁻¹¹ − (гравитацоинная постоянная),

R − расстояние между центрами двух тел,

M₁ и M₂ − массы тел.

Мы знаем, что сила тяжести находится как

Приравняем выше приведенные формулы, немного «покрутим» их и получим, что свободное падение для любой планеты можно найти, зная ее массу и радиус:

А если еще вспомнить второй закон ньютона и ускорение для центростремительного ускорения:

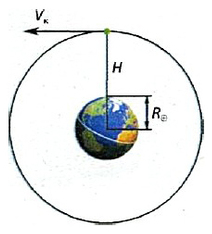
Для нахождение скорости спутника около поверхности планеты применяется формула:

А вот для скорости на расстоянии «H» от Земли, формула будет такой:

С помощью этой же формулы можно найти и первую космическую скорость — это минимальная скорость, которую необходимо придать телу, чтобы он совершал движение по круговой орбите вокруг планеты и не упал обратно на планету (это как с ведром воды, если раскрутить его до большой скорости, вода выливаться не будет и начнет оказывать все большее давление на дно ведра). 

Проще говоря, для выхода на околоземную орбиту (160-2000 км от поверхности) требуется достичь данной скорости, иначе Земля притянет тело обратно. Первая космическая скорость для орбиты, расположенной вблизи поверхности Земли, составляет чуть меньше 8 км/с. 

А для упрощения первую космическую скорость можно из формулы (2) и (3) :

Если есть первая космическая, значит, есть и другие? Конечно есть:

υ₂ — минимальная скорость, которую нужно развить, чтобы начать отдаляться от Земли (11,2 км/с).

υ₃ — скорость «ухода» из Солнечной системы. Самая большая сила потребуется, чтобы «оторваться» от притяжения Солнца. Точного значения здесь нет, т.к. все зависит от того, в каком направлении будет двигаться спутник. Диапазон скоростей без учета влияния других планет солнечной системы составляет от 16,6 км/с до 72,8 км/с.

υ₄ — скорость «ухода» из Галактики. Еще больше неизвестных факторов для определения этой скорости. Но точно потребуется не меньше 220 км/с!  Полет от Москвы до Лос-Анджелеса за 44 секунды?

С помощью формул (1), (2), (3) можно решить почти все задачи на данную тему.

Да — да, рекомендую их выучить, на худой конец записать!

Задача №1. C какой силой притягиваются два корабля массой 50000 т на расстоянии 100 м от центров друг друга?

Закон всемирного тяготения действует на любые тела, но его сила зависит от массы тел, поэтому, чем больше массы, тем больше сила!

Массы двух кораблей знаем (нужно перевести в кг), расстояние между их центрами знаем, остается подставить и посчитать:

Ответ: 17 Н.

Задача №2. Ускорение свободного падения на поверхности Юпитера 24,9 м/с², а радиус планеты 7,13×10⁷ м. Вычислите среднюю плотность планеты.

Зная ускорение свободного падения и радиус, можно найти массу планеты:

Напомню, что плотность находится делением массы на объем.

А как же найти объем? Форму планеты можно принять за шар, а объем шара:

Подставив значения, получим, что плотность Юпитера чуть больше плотности воды, это и не удивительно, она же газовый гигант:

Ответ: 1250 кг/м³.

Задача №3. На каком расстоянии от центра Земли период обращения искусственного спутника будет равен 24 часам, так что спутник сможет занимать относительно вращающейся Земли неизменное положение (период обращения Земли равен периоду обращения спутника, называется такой спутник геостационарный).

Составители задачек считают незнание массы Земли плохим тоном. Но мне несложно напомнить: M = 6×10²⁴ кг.

Ух, ну и задачка! Какой-то период дан, которого ни в какой формуле нет.

В этой задаче для упрощения вывода формул зададим расстояние от центра до спутнка, как R.

Не сомневаюсь, что ты знаешь, что время в равномерном движении — это путь, деленный на скорость.

А если мы движемся по окружности, то время, за которое пройдем целый круг, можно назвать периодом, а путь — длиной окружности.

Чтобы спутник находился на одном расстоянии от центра Земли, воспользуемся формулой (3):

Дело за малым: подставить в формулу периода формулу скорости.

Осталось выразить радиус и подставить числа:

Еще один скользкий момент: T = 24 ч = 1440 м = 86400 с. 

Ответ: 42 тыс. км.

Задача №4 (c ЕГЭ). Известно, что один оборот вокруг своей оси Венера совершает примерно за 243 земных суток, а масса Венеры составляет 0,82 от массы Земли. На орбиту какого радиуса надо вывести спутник Венеры, чтобы он всё время «висел» над одной и той же точкой поверхности? Известно, что спутники Земли, «висящие» над одной и той же точкой поверхности, летают по орбите радиусом R = 42000 км.

Данная задачка чем-то напоминает предыдущую. Честно говоря, это почти та же самая задача. Только тут спрашивается про спутник Венеры

Начать предлагаю с доказательства, что геостационарная орбита Земли находится на расстоянии 42000 км: 

Нас не обманули! Получается, что геостационарный спутник имеет период обращения 1 сутки, как и Земля.

Что же касается Венеры, то тут период должен составлять 243 суток = 20995200 секунд.

А масса Венеры 0,82×6×10²⁴ кг.

Подставляем в ту же формулу, что и в предыдущей задаче:

Ответ: 1530 тыс. км.

Задача №5. Средняя плотность планеты Плюк равна средней плотности планеты Земля, а радиус Плюка в два раза больше радиуса Земли. Во сколько раз первая космическая скорость для Плюка больше, чем для Земли?

Для начала разберемся, как же отличаются массы. Для этого представим массу Плюка и Земли через плотность и объем Земли:

Скорость можно найти по любой из этих двух формул:

Проще всего воспользоваться первой, зная, во сколько раз отличаются массы и радиусы, получим ответ.

Ответ: 2

Сложность этой темы в большей степени заключается в рассчетах: числа большие, степени сложные. А вот обилием формул эта тема не похвастается, все основные представлены в начале. 

Так же не забывай проверять себя «на глупость»: масса планеты, скорее всего, не может быть 1000 т, а космическая скорость — 120 м/с.

Будь в курсе новых статеек, видео и легкого технического юмора.

Вот такая задача. Есть планета, для простоты — сферическая, не вращающаяся, по составу однородная. Масса планеты [math]M[/math] известна ([math]M=frac{ 4 }{ 3 } cdot pi R^{3} cdot rho_ {R}[/math], где [math]R[/math] — радиус планеты, [math]rho _{R}[/math] — средняя плотность планеты). Коэффициент сжимаемости [math]beta[/math] материала, из которого сделана планета, известен ([math]beta = frac{ 1 }{ rho } cdot frac{ d rho }{ dP }[/math], где [math]rho[/math] — плотность, [math]P[/math] — давление). Плотность наружного слоя [math]rho _{0}[/math] — плотность при нулевом давлении — известна (ее, наверное, удобно за единицу принять). Очевидно, что этих данных достаточно, чтобы найти радиус планеты [math]R[/math]. Но вот как его найти — ума не приложу.
Понятно, что на расстоянии [math]r[/math] от центра планеты ([math]r<R[/math]) давление от вышележащих слоев [math]P_{r} = frac{ g_{r}left( M — M_{r} right) }{ 4 pi r^{2} }[/math], где [math]g_{r}[/math] — ускорение свободного падения на глубине [math]R-r[/math], [math]M_{r}[/math] — масса сферы с радиусом [math]r[/math]. [math]M_{r}=frac{ 4 }{ 3 } cdot pi r^{3} cdot rho _{r}[/math], [math]g_{r}=frac{ G cdot M_{r} }{ r^{2} }= frac{ 4 }{ 3 } cdot G pi r cdot rho _{r}[/math], где [math]rho _{r}[/math] — средняя плотность сферы с радиусом [math]r[/math], [math]G[/math] — гравитационная постоянная. Отсюда [math]P_{r}=frac{ 4G pi rho _{r}(R^{3} rho _{R}-r^{3} rho _{r}) }{ 9r }[/math]. А как же [math]P_{r}[/math], [math]rho _{R}[/math] и [math]rho _{r}[/math] выразить через [math]beta[/math]? Никто не подскажет?