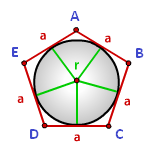
Радиус вписанной окружности в правильный многоугольник
a — сторона многоугольника
N — количество сторон многоугольника
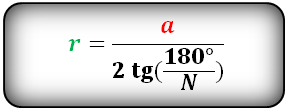
Формула радиуса вписанной окружности в правильный многоугольник, (r):
Калькулятор — вычислить, найти радиус вписанной окружности в правильный многоугольник
- Подробности
-
Автор: Administrator
-
Опубликовано: 10 сентября 2011
-
Обновлено: 13 августа 2021
Радиус вписанной окружности в правильный многоугольник, формула
|
Правильный многоугольник — это многоугольник с равными сторонами и углами. Угол между двумя соседними вершинами правильного n-угольника равен: [AOB = α = frac{360°}{n}] |
 |
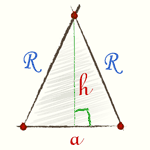 |
Построим треугольник AOB отдельно. Об этом треугольнике мы знаем: он равнобедренный, и высота этого треугольника это радиус вписанной окружности правильного многоугольника. Также нам известна длина основания a этого треугольника — которое является стороной исходного правильного многоугольника. |
Также известен угол между бедрами — по формуле (1).
Опустим высоту на основание и рассмотрим получившийся прямоугольный треугольник.
При помощи тригонометрических функций острого угла получим:
[tgbigg(frac{360°}{2n}bigg) = frac{a}{2r}]
отсюда получим формулу радиуса вписанной окружности правильного многоугольника:
[r = frac{a}{2 tg(frac{360°}{2n})}]
(a — сторонa правильного многоугольника; n — число сторон правильного многоугольника; r — радиус вписанной окружности правильного многоугольника)
Вычислить, найти радиус вписанной окружности в правильный многоугольник по формуле (3)
Радиус вписанной окружности в правильный многоугольник |
стр. 256 |
|---|
Правильный многоугольник. Формулы, признаки и свойства правильного многоугольника
Определение. Правильный многоугольник — это многоугольник, у которого все стороны и углы одинаковые.
Многоугольником называется часть площади, которая ограничена замкнутой ломаной линией, не пересекающей сама себя.
Многоугольники отличаются между собой количеством сторон и углов.
Признаки правильного многоугольника
Многоугольник будет правильным, если выполняется следующее условие:
Все стороны и углы одинаковы:
a1 = a2 = a3 = … = an-1 = an
α1 = α2 = α3 = … = αn-1 = αn
Основные свойства правильного многоугольника
1. Все стороны равны:
a1 = a2 = a3 = … = an-1 = an
2. Все углы равны:
α1 = α2 = α3 = … = αn-1 = αn
3. Центр вписанной окружности Oв совпадает з центром описанной окружности Oо, что и образуют центр многоугольника O
4. Сумма всех углов n-угольника равна:
180° · (n — 2)
5. Сумма всех внешних углов n-угольника равна 360°:
β1 + β2 + β3 + … + βn-1 + βn = 360°
6. Количество диагоналей (Dn) n-угольника равна половине произведения количества вершин на количество диагоналей, выходящих из каждой вершины:
7. В любой многоугольник можно вписать окружность и описать круг при этом площадь кольца, образованная этими окружностями, зависит только от длины стороны многоугольника:
8. Все биссектрисы углов между сторонами равны и проходят через центр правильного многоугольника O
Правильный n-угольник — формулы
Формулы длины стороны правильного n-угольника
1. Формула стороны правильного n-угольника через радиус вписанной окружности:
2. Формула стороны правильного n-угольника через радиус описанной окружности:
Формула радиуса вписанной окружности правильного n-угольника
Формула радиуса вписанной окружности n-угольника через длину стороны:
Формула радиуса описанной окружности правильного n-угольника
Формула радиуса описанной окружности n-угольника через длину стороны:
Формулы площади правильного n-угольника
1. Формула площади n-угольника через длину стороны:
2. Формула площади n-угольника через радиус вписанной окружности:
3. Формула площади n-угольника через радиус описанной окружности:
Формула периметра правильного многоугольника:
Формула периметра правильного n-угольника:
P = na
Формула определения угла между сторонами правильного многоугольника:
Формула угла между сторонами правильного n-угольника:
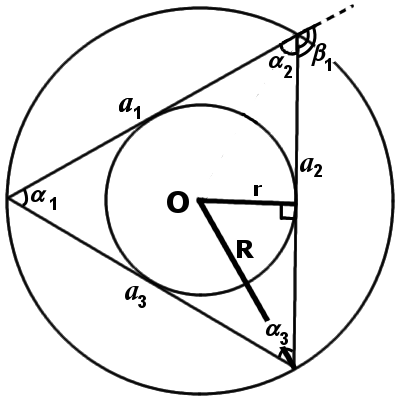 |
| Рис.3 |
Правильный треугольник
Формулы правильного треугольника:
1. Формула стороны правильного треугольника через радиус вписанной окружности:
a = 2r √3
2. Формула стороны правильного треугольника через радиус описанной окружности:
a = R√3
3. Формула радиуса вписанной окружности правильного треугольника через длину стороны:
4. Формула радиуса описанной окружности правильного треугольника через длину стороны:
5. Формула площади правильного треугольника через длину стороны:
6. Формула площади правильного треугольника через радиус вписанной окружности:
S = r2 3√3
7. Формула площади правильного треугольника через радиус описанной окружности:
8. Угол между сторонами правильного треугольника:
α = 60°
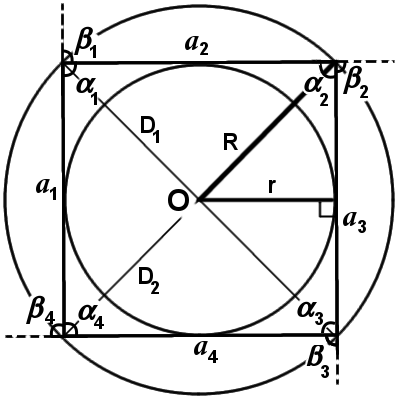 |
| Рис.4 |
Правильный четырехугольник
Правильный четырехугольнику — квадрат.
Формулы правильного четырехугольника:
1. Формула стороны правильного четырехугольника через радиус вписанной окружности:
a = 2r
2. Формула стороны правильного четырехугольника через радиус описанной окружности:
a = R√2
3. Формула радиуса вписанной окружности правильного четырехугольника через длину стороны:
4. Формула радиуса описанной окружности правильного четырехугольника через длину стороны:
5. Формула площади правильного четырехугольника через длину стороны:
S = a2
6. Формула площади правильного четырехугольника через радиус вписанной окружности:
S = 4 r2
7. Формула площади правильного четырехугольника через радиус описанной окружности:
S = 2 R2
8. Угол между сторонами правильного четырехугольника:
α = 90°
Правильный шестиугольник
Формулы правильного шестиугольника:
1. Формула стороны правильного шестиугольника через радиус вписанной окружности:
2. Формула стороны правильного шестиугольника через радиус описанной окружности:
a = R
3. Формула радиуса вписанной окружности правильного шестиугольника через длину стороны:
4. Формула радиуса описанной окружности правильного шестиугольника через длину стороны:
R = a
5. Формула площади правильного шестиугольника через длину стороны:
6. Формула площади правильного шестиугольника через радиус вписанной окружности:
S = r2 2√3
7. Формула площади правильного шестиугольника через радиус описанной окружности:
8. Угол между сторонами правильного шестиугольника:
α = 120°
Правильный восьмиугольник
Формулы правильного восьмиугольника:
1. Формула стороны правильного восьмиугольника через радиус вписанной окружности:
a = 2r · (√2 — 1)
2. Формула стороны правильного восьмиугольника через радиус описанной окружности:
a = R√2 — √2
3. Формула радиуса вписанной окружности правильного восьмиугольника через длину стороны:
4. Формула радиуса описанной окружности правильного восьмиугольника через длину стороны:
5. Формула площади правильного восьмиугольника через длину стороны:
S = a2 2(√2 + 1)
6. Формула площади правильного восьмиугольника через радиус вписанной окружности:
S = r2 8(√2 — 1)
7. Формула площади правильного восьмиугольника через радиус описанной окружности:
S = R2 2√2
8. Угол между сторонами правильного восьмиугольника:
α = 135°
В публикации представлена формула, с помощью которой можно найти радиус окружности, вписанной в правильный многоугольник, а также приведен пример решения задачи для лучшего понимания представленного материала.
- Формула расчета радиуса окружности
- Пример задачи
Формула расчета радиуса окружности
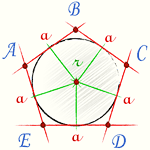
На рисунке изображен правильный шестиугольник со вписанной в него окружностью, но формула ниже подходит для любого правильного n-угольника.
где a – длина стороны.
Примечание: зная радиус вписанного круга можно найти сторону равностороннего n-угольника:
Пример задачи
Вычислите радиус вписанной в правильный восьмиугольник окружности, если длина его стороны составляет 12 см.
Решение:
Воспользуемся первой формулой, подставив в нее известное значение.
-
Радиус вписанной окружности правильного многоугольника
Свойства
Зная радиус вписанной окружности в правильный – равносторонний многоугольник и количество сторон в нем, можно найти длину одной стороны, как произведение удвоенного радиуса на тангенс угла 180 градусов, деленных на количество сторон.
a=2r tan〖(180°)/n〗Если подставить полученное для стороны выражение в формулу радиуса описанной окружности, то получится радиус вписанной окружности, разделенный на косинус того же угла.
R=a/(2 sin〖(180°)/n〗 )=(2r tan〖(180°)/n〗)/(2 sin〖(180°)/n〗 )=r/cos〖(180°)/n〗Чтобы найти площадь правильного многоугольника через радиус вписанной окружности, нужно полученное выражение возвести во вторую степень, и преобразовать формулу, упростив ее.
S=(na^2)/(4 tan〖(180°)/n〗 )=(n(2r tan〖(180°)/n〗 )^2)/(4 tan〖(180°)/n〗 )=nr^2 tan〖(180°)/n〗Периметр правильного многоугольника, как и любой другой фигуры, равен сумме длин всех ее сторон, поэтому чтобы его вычислить через радиус, нужно произведение удвоенного радиуса и указанного угла умножить еще на количество сторон.
P=na=2rn tan〖(180°)/n〗Угол правильного многоугольника зависит исключительно от количества сторон и никоим образом от их длины, и доказательством этому служит формула величины внутреннего угла, включающая в себя только одну переменную.
α=(n-2) (180°)/n