Как найти радиус впис окруж

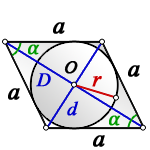
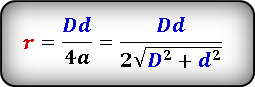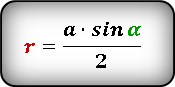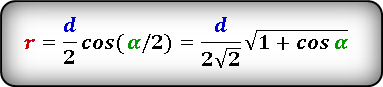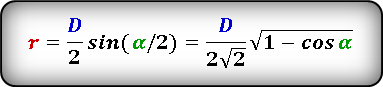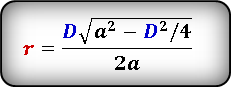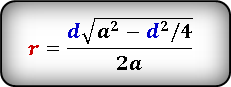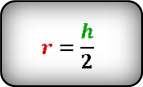1. Формулы радиуса вписанной окружности если известны: диагональ, стороны и угол

a — сторона ромба

D — большая диагональ

d — меньшая диагональ

α — острый угол

О — центр вписанной окружности

r — радиус вписанной окружности

Формула радиуса вписанной окружности в ромб через диагонали ( r ) :

Формула радиуса вписанной окружности в ромб через сторону и угол ( r ) :

Формула радиуса вписанной окружности в ромб через диагональ и угол ( r ) :

Формула радиуса вписанной окружности в ромб через диагональ и сторону ( r ) :

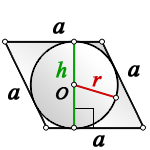
2. Радиус вписанной окружности ромба, равен половине его высоты

a — сторона ромба

h — высота

О — центр вписанной окружности

r — радиус вписанной окружности

Формула радиуса вписанной окружности в ромб ( r ) :

Вписанная окружность — в какую фигуру нельзя вписать

Для решения геометрических задач можно использовать различные формулы и приемы, которые помогут облегчить поиск искомых показателей. Один из способов найти различные неизвестные в многогранной фигуре – сделать это через вписанную окружность.

Вписанная окружность — окружность, которая лежит внутри угла и касается его сторон. Касание происходит в одной точке с каждой стороны. 

Вписанная в фигуру окружность, например, в треугольник или многоугольник, будет касаться всех его сторон. Это главное свойство окружности, которая будет называться вписанной. Сама фигура в таком случае называется описанной вокруг окружности.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Окружность точно можно вписать в следующие геометрические фигуры:

• треугольник;
• выпуклый правильный многоугольник;
• квадрат;
• равнобедренная трапеция;
• ромб.

При этом окружность в данные фигуры может быть вписана лишь единожды.

Четырехугольник является неоднозначной фигурой при процессе вписывания в нее окружности. Для того, чтобы окружность была вписанной в четырехугольник, суммы длин его противоположных сторон должны быть равны.

Окружность точно нельзя вписать в следующие геометрические фигуры:

• прямоугольник;
• параллелограмм (если он не является ромбом).

Ни один из видов данных фигур не сможет иметь вписанную окружность, так как она не сможет соприкасаться со всеми их сторонами, что является главным признаком вписанной окружности.

Теорема о вписанной окружности

Теорема о вписанной окружности гласит, что в любой треугольник и в любой выпуклый многоугольник и четырехугольник с равными суммами длин противоположных сторон можно вписать окружность, но только одну.

Правило о центре вписанной окружности

Центр окружности при этом будет находиться в точке пересечения биссектрис фигуры. Чтобы определить центр, нужно построить биссектрисы из каждого угла и найти пересечение.

Формула нахождения радиуса вписанной окружности

Вычисление радиуса вписанной окружности ведется по формулам, которые зависят от фигуры и известных данных. Главным условием является тот факт, что фигура должна подходить под список тех, в которые можно вписать окружность.

Радиус — перпендикуляр, соединяющий центр окружности с любой точкой, лежащей на окружности. По длине радиус составляет половину диаметра.

Треугольник

Формула нахождения радиуса окружности, вписанной в треугольник через все стороны:

(r=sqrt{frac{left(p-aright)left(p-bright)left(p-cright)}p},)

где r — радиус,

a, b и c — стороны треугольника,

p — полупериметр, (p=frac{a+b+c}2.)

Формула нахождения радиуса окружности, вписанной в треугольник через сторону и высоту:

(r=frac{btimes h}{b+sqrt{4times h^2+b^2}},)

(r=frac{htimessqrt{a^2-h^2}}{a+sqrt{a^2-h^2}},)

где r — радиус,

a и b — стороны треугольника,

h — высота.

Равносторонний треугольник

Формула нахождения радиуса окружности, вписанной в равносторонний треугольник:

(r=frac a{2sqrt3},)

где r — радиус,

a — сторона треугольника.

Равнобедренный треугольник

Формула нахождения радиуса окружности, вписанной в равнобедренный треугольник через значения сторон:

(r=frac b2sqrt{frac{2a-b}{2a+b}},)

где r — радиус,

a и b — стороны треугольника.

Формула нахождения радиуса окружности, вписанной в равнобедренный треугольник через сторону и угол:

(r=Atimesfrac{sinleft(aright)timescosleft(aright)}{1+cosleft(aright)}= Atimescosleft(aright)timestanleft(frac a2right),)

(r=frac b2timesfrac{sinleft(aright)}{1+cosleft(aright)}=frac b2timestanleft(frac a2right),)

где r — радиус,

A и b — стороны треугольника,

a — угол при основании.

Прямоугольный треугольник

Формула нахождения радиуса окружности, вписанной в прямоугольный треугольник:

(r=frac{atimes b}{a+b+c}=frac{a+b-c}2,)

где r — радиус,

a и b — катеты треугольника,

c — гипотенуза.

Равнобедренная трапеция

Формула нахождения радиуса окружности, вписанной в равнобедренную трапецию:

(r=frac h2=frac{sqrt{ctimes b}}2,)

где r — радиус,

с — нижнее основание,

b — верхнее,

а — боковые стороны,

h — высота.

Квадрат

Формула нахождения радиуса окружности, вписанной в квадрат:

(r=frac a2,)

где r — радиус,

а — сторона квадрата.

Ромб

Формула нахождения радиуса окружности, вписанной в ромб через значения диагоналей:

(r=frac{Dtimes d}{4times a}=frac{Dtimes d}{2sqrt{D^2+d^2}}.)

Формула нахождения радиуса окружности, вписанной в ромб через значения стороны и угла:

(r=frac{atimessinleft(aright)}2.)

Формула нахождения радиуса окружности, вписанной в ромб через диагональ и угол:

(r=frac d2timescosleft(frac a2right)=frac d{2sqrt2}timessqrt{1+cosleft(aright)},)

(r=frac D2timessinleft(frac a2right)=frac D{2sqrt2}timessqrt{1-cosleft(aright)}.)

Формула нахождения радиуса окружности, вписанной в ромб через диагональ и сторону:

(r=frac{Dsqrt{a^2-{displaystylefrac{D^2}4}}}{2a},)

(r=frac{dsqrt{a^2-{displaystylefrac{d^2}4}}}{2a}.)

Формула нахождения радиуса окружности, вписанной в ромб через высоту:

(r=frac h2,)

где r — радиус,

а — сторона ромба,

D — большая диагональ,

d — меньшая диагональ,

a — острый угол,

h — высота.

Многоугольник

Формула нахождения радиуса окружности, вписанной в правильный многоугольник:

(r=frac a{2timestanleft({displaystylefrac{180^circ}N}right)},)

где r — радиус,

N — количество сторон многоугольника.

Шестиугольник

Формула нахождения радиуса окружности, вписанной в шестиугольник:

(r=frac{sqrt3}2times a,)

где r — радиус,

a — сторона шестиугольника.

Удобно, когда все формулы, по которым можно найти радиус вписанной в треугольник и в многоугольник окружности, размещены на одной странице.

Радиус вписанной в многоугольник окружности

Если в многоугольник можно вписать окружность, то формула для вычисления радиуса вписанной окружности:

где p — полупериметр, то есть полусумма длин всех сторон этого многоугольника.

Например, для пятиугольника со сторонами a, b, c, d, e радиус вписанной окружности находится по формуле

откуда

По этой же формуле ищут радиус вписанной в треугольник окружности.

Радиус вписанной в треугольник окружности

Формула для нахождения радиуса вписанной в треугольник окружности (верна для треугольника любого вида)

где p — полупериметр,

где a, b, c — стороны треугольника.

Радиус вписанной в прямоугольный треугольник окружности

Формула для нахождения радиуса окружности, вписанной в прямоугольный треугольник

где a и b — катеты, c — гипотенуза.

Радиус окружности, вписанной в правильный многоугольник

Формула радиуса вписанной в правильный многоугольник окружности

где a — сторона многоугольника, n — количество сторон.

Частные случаи — правильный (равносторонний) треугольник, правильный четырехугольник (квадрат) и правильный шестиугольник.

Радиус окружности, вписанной в правильный треугольник

Формула радиуса вписанной окружности для правильного треугольника:

В правильном треугольнике радиус вписанной окружности вдвое меньше радиуса описанной окружности:

Радиус окружности, вписанной в квадрат

Формула радиуса вписанной в квадрат окружности:

где a — сторона квадрата.

Радиус окружности, вписанной в правильный шестиугольник

Формула радиуса вписанной в правильный шестиугольник окружности:

где a — сторона правильного шестиугольника.

Для любого многоугольника центр вписанной окружности лежит в точке пересечения его биссектрис.

Вписанная окружность и отрезки сторон треугольника

Давай представим, что мы откуда-то узнали все три стороны треугольника.

Можно ли найти как-то отрезочки ( displaystyle AK), ( displaystyle KC), ( displaystyle BL) и.д. —отрезки, на которые точки касания разбивают стороны треугольника?

Представь себе, можно, и даже очень легко. Для этого нужно знать только то, что отрезки касательных, проведённых из одной точки, равны (если ещё не успел это узнать – загляни в тему «Касательные, касающиеся окружности»).

Итак, начнём поиск!

Посмотри внимательно: из точки ( displaystyle A) проведено две касательных, значит их отрезки ( displaystyle AK) и ( displaystyle AM) равны.

Мы обозначим их «( displaystyle x)».

Далее, точно так же:

( displaystyle BM=BL=y) (обозначили).

( displaystyle CK=CL=z) (обозначили).

Теперь вспомним-ка, что мы знаем длины всех трёх сторон треугольника. Обозначим эти длины «( displaystyle a)», «( displaystyle b)», «( displaystyle c)» — смотри на рисунок. Что же теперь получилось?

А вот, например, отрезок «( displaystyle a)» состоит из двух отрезков «( displaystyle y)» и «( displaystyle z)», да и отрезки «( displaystyle b)» и «( displaystyle c)» тоже из чего-то состоят. Запишем это всё сразу:

Сложим первые два уравнения и вычтем третье:

( displaystyle left{ begin{array}{l}y+z=a\x+z=b\x+y=cend{array} right.Rightarrow x+y+2z-left( x+y right)=a+b-c), то есть:

( displaystyle z=frac{a+b-c}{2})

А теперь сложим первое и третье уравнение и вычтем второе:

( displaystyle left{ begin{array}{l}y+z=a\x+z=b\x+y=cend{array} right.Rightarrow y+z+x+y-left( x+z right)=a+c-b), то есть:

( displaystyle y=frac{a+c-b}{2})

И последний шаг: сложим второе и третье, а потом вычтем первое.

( displaystyle left{ begin{array}{l}y+z=a\x+z=b\x+y=cend{array} right.Rightarrow x=frac{b+c-a}{2})

( displaystyle x=frac{b+c-a}{2})

Ну вот, всё нашли:

( displaystyle x=frac{b+c-a}{2};y=frac{a+c-b}{2};~z=frac{a+b-c}{2})

Очень много плюсов и минусов – аж в глазах рябит. Как же это запомнить? А оказывается, очень просто. Смотри-ка на картинку и формулу сразу.

( displaystyle x=frac{b+c-a}{2})

Секрет вот в чём: те стороны, на которых есть «( displaystyle x)» («( displaystyle b)» и «( displaystyle c)») будут с плюсом, а та сторона, где нет «( displaystyle x)» (это «( displaystyle a)»), будет с минусом.

Ну, а пополам поделить всё хозяйство. С другими буквами точно так же

В любой треугольник можно вписать окружность. Радиус такой окружности будет представлять собой квадратный корень из отношения разности полупериметра с каждой стороной к самому полупериметру.

Если упростить данную формулу для прямоугольного треугольника, воспользовавшись теоремой Пифагора, то мы получим следующее выражение:

Так как в равнобедренном треугольнике боковые стороны равны, то в формуле остаются только обозначения a и b, и ее вид упрощается из все того же первого радикала до следующей формы:

В случае с равносторонним треугольником все еще гораздо проще, и его формула может быть выведена не только из формулы для произвольного треугольника, но также и из свойств высоты-медианы-биссектрисы, которые совпадают и делят любую из сторон на две равные части: