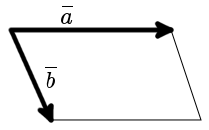
Найти четвертую вершину параллелограмма
Как найти координаты 4-й вершины параллелограмма, зная координаты трёх других его вершин?
В декартовых координатах эту задачу можно решить, используя свойство диагоналей параллелограмма.
Из трёх известных вершин две являются концами одной диагонали. Находим координаты середины этой диагонали. Точка пересечения диагоналей является серединой каждой из них. Для второй диагонали находим второй конец по известным одному концу и середине.
Дано: ABCD — параллелограмм,
1) Найдём координаты точки O — середины диагонали AC.
2) По свойству диагоналей параллелограмма, точка O также является серединой BD:
Дано: ABCD — параллелограмм,
1) Ищем координаты точки O — середины отрезка BD:
2) Точка O также является серединой AC:
2 Comments
А как вы получили -14 в первом примере.
Можно применить основное свойство пропорции: 12+xD=2∙(-1), xD=-2-12=-14.
Диагонали параллелограмма ВСЕН пересекаются в начале координат. Найдите радиус-векторы его вершин, если В(-3; 2), ОС <1;-4>. Начертите параллелограмм ВСЕН.
Ваш ответ
решение вопроса
Похожие вопросы
- Все категории
- экономические 43,277
- гуманитарные 33,618
- юридические 17,900
- школьный раздел 606,812
- разное 16,824
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Даны радиус векторы трех последовательных вершин параллелограмма
Ответ
Проверено экспертом
Прямая BC имеет вид y=bx+c
Составим систему уравнений:
Прямая BC описывается уравнением
y=-0,2x+8,8
Прямая AD || BC, значит коэффициент b у них одинаковый, отличается только коэффициент с. Можем составить уравнение прямой, проходящей через точку A, параллельную BC
y=bx+c
2=-0,2*2+c
c=2,4
y=-0,2x+2,4
Прямая AB имеет вид y=bx+c
Составим систему уравнений:
Прямая AB описывается уравнением
y=3x-4
Прямая CD || AB, значит коэффициент b у них одинаковый, отличается только коэффициент с. Можем составить уравнение прямой, проходящей через точку С, параллельную АВ
y=bx+c
10=-6*3+c
c=28
y=3x+28
Координаты точки D:
-0,2x+2,4=3x+28
3,2x=-25,6
x=-8
По точкам можно построить параллелограмм ABCD и убедиться в правильности решения
Даны три последовательные вершины параллелограмма А(-2;1),В(1;3),С(4;0). Найти четвертую его координату D. Система координат аффинная.
Векторы 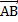
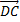
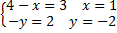
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Сдача сессии и защита диплома — страшная бессонница, которая потом кажется страшным сном. 8799 — 

78.85.5.224 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
Этот онлайн калькулятор позволит вам очень просто найти площадь параллелограмма построенного на векторах.
Воспользовавшись онлайн калькулятором, вы получите детальное решение вашей задачи, которое позволит понять алгоритм решения задач на вычисление площади параллелограмма построенного на векторах и закрепить пройденый материал.
Калькулятор для вычисления площади параллелограмма построенного на векторах
Выберите каким образом задается параллелограмм:
Введите значения векторов: Введите координаты трех любых вершин параллелограмма:
Инструкция использования калькулятора для вычисления площади параллелограмма построенного на векторах
Ввод данных в калькулятор для вычисления площади параллелограмма построенного на векторах
В онлайн калькулятор вводить можно числа или дроби. Более подробно читайте в правилах ввода чисел.
Дополнительные возможности калькулятора вычисления площади параллелограмма построенного на векторах
- Между полями для ввода можно перемещаться нажимая клавиши «влево» и «вправо» на клавиатуре.
Теория. Площадь параллелограмма построенного на векторах.
Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел.
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
http://www.soloby.ru/704318/%D0%B4%D0%B8%D0%B0%D0%B3%D0%BE%D0%BD%D0%B0%D0%BB%D0%B8-%D0%BF%D0%B0%D1%80%D0%B0%D0%BB%D0%BB%D0%B5%D0%BB%D0%BE%D0%B3%D1%80%D0%B0%D0%BC%D0%BC%D0%B0-%D0%BF%D0%B5%D1%80%D0%B5%D1%81%D0%B5%D0%BA%D0%B0%D1%8E%D1%82%D1%81%D1%8F-%D0%BF%D0%B0%D1%80%D0%B0%D0%BB%D0%BB%D0%B5%D0%BB%D0%BE%D0%B3%D1%80%D0%B0%D0%BC%D0%BC
http://gadget-apple.ru/dany-radius-vektory-treh-posledovatelnyh-vershin.html
|
0 / 0 / 0 Регистрация: 19.07.2013 Сообщений: 20 |
|
|
1 |
|
Зная радиус-векторы найти радиус-вектор вершины28.04.2015, 22:05. Показов 14805. Ответов 3
Даны радиус-векторы r1,r2,r3, трех последовательных вершин A, B, и С параллелограмма. Найти радиус-вектор четвертой вершины D. Помогите решить пожалуйста.
0 |
|
3971 / 2950 / 894 Регистрация: 19.11.2012 Сообщений: 6,063 |
|
|
29.04.2015, 07:10 |
2 |
|
r4=(r1-r2)+(r3-r2).
0 |
|
3944 / 2858 / 665 Регистрация: 08.06.2007 Сообщений: 9,668 Записей в блоге: 4 |
|
|
30.04.2015, 13:37 |
3 |
|
Это диагональ получится. Надо еще добавить радиус-вектор точки 2.
1 |
|
3971 / 2950 / 894 Регистрация: 19.11.2012 Сообщений: 6,063 |
|
|
30.04.2015, 14:53 |
4 |
|
Надо еще добавить радиус-вектор точки 2. Да, конечно.
0 |
поделиться знаниями или
запомнить страничку
- Все категории
-
экономические
43,662 -
гуманитарные
33,654 -
юридические
17,917 -
школьный раздел
611,978 -
разное
16,905
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Единственна ли такая точка?1 3 . 16 . 1 . Решить задачу, аналогичную задаче 1 3 . 1 6 , для параллелограмма.1 3 . 1 6 . 2 . Решить задачу, аналогичную задаче 1 3 . 1 6 , для произвольного четырехугол�ника.�1 3 . 17. От точки О отложены два ненулевых вектора ОА = а��и ОБ = Ь. Найти какой-нибудь вектор ОМ , идущий по биссектрисе угла АО В .1 3 . 18. В треугольнике АБС проведена биссектриса AD угла���А. Выразить вектор AD через векторы АВ и АС.1 3 . 1 9 . В треугольнике АБС биссектрисы AL и ВК пересе��каются в точке О. Выразить векторы АО и ВО через векторы—-t�Ь = АВ и с = АС , если известны длины сторон треугольника:а == I BC I , Ь = I ACI , с = I AB I .
Вывести отсюда теорему о точкепересечения биссектрис в треугольнике.1 3 . 20 . Через точку Р медианы СС1 треугольника АБС проведены прямые АА 1 и ВВ 1 (точки A i и В 1 лежат на сторонах—-tВС и СА ) . Доказать, что векторы Ai B 1 и АВ коллинеарны.1 3 . 2 1 . а) Точки А , В и С лежат на одной прямой, а точки A i ,Вдругой прямой. Доказать, что из коллинеарности1 и С—71 на��—7-tАВ 1 и ВА 1 , АС1 и СА 1 следует коллинеарность ВС1 и СВ 1 .б) То ч ки А , В и С лежат на одной прямой, а точки A i , В 1�-t�-t�и С1 таковы, что пары векторов АВ 1 и ВА 1 , АС1 и СА 1 , ВС1-tи СВ 1 коллинеарны.
Доказать , что точки Ai , В 1 и С1 лежат наодной прямой.��1 3 . 2 2 . Пусть АВ = а , АС = Ь — неколлинеарные векторы�и М точка на прямой ВС . Доказать, что АМ = а а + ,В Ь, гдеа + ,В = 1 . Что можно сказать о числах а и ,В, если точка Млежит:—1 23§1 3. Геометрические векторыа) на стороне БС;б) внутри треугольника АБС ;в) вне треугольника АБС ?���1 3 . 23 .
Пусть АВ = а, АС = Ь, AD = с некомпланарныевекторы и М точка плоскости, проходящей через точки Б , С—tи D. Доказать , что А М = а а + ,В Ь + / с , где а + ,В + / = 1 . Чтом ожно сказать о числах а, ,В и { , если точка М лежит:а) на грани БСD ;б ) внутри тетраэдра АБСD ;в) вне тетраэдра АБСD ?��1 3 . 24. На трех некомпланарных векторах АВ = р , A D = q ,—-+АА’ = r построен параллелепипед АВ С D А’ Б’ С ‘ D’. Выразитьчерез р, q и r векторы , совпадающие с ребрами, диагональюпараллелепипеда и диагоналями граней этого параллелепипеда,для которых вершина А’ служит началом .1 3 . 25 . В тетраэдре АБСD даны ребра, выходящие из верши���ны А: АБ = Ь , АС = с и A D = d . Выразить через эти векторы�остальные ребра тетраэдра, медиану DM грани БСD и вектор�AQ , где Q — точка пересечения медиан грани БСD.��1 3 . 26. Дан тетраэдр ОАБС .
Полагая ОА = а , ОБ = Ь и���-tОС = с , выразить через а , Ь и с векторы MN, PQ и RS , вкоторых М, Р и R — середины ребер ОА, ОБ и ОС , а N , Q и Sсередины соответствующих противоположных ребер.��1 3 . 27. Дан тетраэдр ОАБС . Полагая ОА = а , ОБ = Ь и�—-tОС = с , выразить через а , Ь и с вектор EF, в котором Е — середина ребра ОА, а F — точка пересечения медиан треугольника—АБС .1 3 . 28 . Даны радиус-векторы r 1 , r2 , rз трех последовательн ых вершин А, Б и С параллелограмма.
Найти радиус-векторчетвертой вершины D .1 3 . 29 . Зная радиус- векторы r 1 , r 2 , rз вершин треугольника,н айти радиус-вектор точки пересечения его медиан.1 3 . 30. Зная радиус-векторы r1 , r2 , rз трех последовательных вершин параллелограмма, найти радиус-вектор r точки пересечения диагоналей параллелограмма.1 3 .
31 . Даны три последовательные вершины трапецииА ( r 1 ) , Б ( r 2 ) и С ( rз ) . Найти радиус-векторы: r4 четвертой вер-1 24Глава IV. Введение в теорию линейных пространствшины D , r’ точки пересечения диагоналей и r» точки пересечения боковых сторон, зная, что основание AD в Л раз большеоснования ВС.1 3 . 32 . Зная радиус-векторы r л , r в , Г D и Г А’ четырех вершин параллелепипеда ABCDA’ В’С’ D’ , найти радиус-векторычетырех остальных его вершин.���1 3 . 33. Радиус-векторы ОА = r 1 , О Б = r 2 и ОС = r з служат ребрами параллелепипеда.
Найти радиус-вектор точки пересечения диагонали параллелепипеда, выходящей из вершиныО , с плоскостью, проходящей через вершины А , В и С.1 3 . 33 . 1 . Зная радиус-векторы r 1 , r 2 , rз , r4 вершин тетраэдра, найти радиус-вектор точки пересечения отрезков , соединяющих середины его противоположных ребер.1 3 . 34. Известно, что ( АБС ) = Л. Найти ( САВ ) .1 3 . 35 .
Известно, что ( АВР ) = Л , ( ABQ ) = µ . Найти ( Р RQ) ,если точка R делит отрезок АВ в отношении v .1 3 . 35 . 1 . Известно, что ( АВР ) = Л, (ABQ) = µ. Найти (ABR) ,если точка R является серединой отрезка PQ .1 3 . 36. Доказать, что если точки К, L , М , N делят в одном итом же отношении Л стороны АВ , ВС , CD , DA параллелограмма ABCD, то четырехугольник KLMN есть параллелограмм .Показать, что если Л -=/= 1 и четырехугольник К L M N являетсяпараллелограммом , то четырехугольник ABCD также параллелограмм .1 3 .
37. Дан тетраэдр ABCD . Найти точку М , для которой—t-+��мл + мв + мс + мп == о .1 3 . 38. От точки М отложены три ненулевых вектора х , у ,z , сумма которых равна нулевому вектору. Зная углы а , {3 , тмежду векторами у и z , z и х , х и у соответственно , найтиотношения длин этих векторов 1 x l : 1 : 1 z l .1 3 . 39 . От точки М , лежащей в плоскости треугольника АБС ,—tотложены три ненулевых вектора х , у, z , сонаправленных МА,� -+МВ , МС соответственно и таких, что х + у + z = О. Найтиотношение длин этих векторов 1 x l : 1 : 1 z l , если :а) точка М является центром окружности, описанной околотреугольника АБС ;б) точка М является центром окружности , вписанной в треугольник АБС;-YIYI§ 1 4 .
Вещественное линейное пространство1 25в) точка М является точкой пересечения высот треугольникаАБС , а сам треугольник АБС остроугольный.1 3 . 40. Найти точку М , лежаI.Цую в плоскости треугольникаАБС , если сумм а трех ненулевых векторов с равнымидлина���ми, отложенных от этой точки и сонаправленных МА, МВ , МСсоответственно , равна нулевому вектору.1 3 .4 1 . Даны два треугольника АБС и А’ В’С’. Выразить вектор ММ’ , соединяющий точки пересечения медиан этих тре���’угольников, через векторы АА , ВВ’ , СС’ .1 3 .42 .
В прямоугольном треугольнике АБС опущен перпен�дикуляр С Н на гипотенузу АВ. Выразить вектор С Н через век��торы СА и СВ и длины катетов I B C I = а и CA I = Ь .1 3 .43. Зная радиус-векторы r 1 , r 2 , r з вершин треугольникаАБС и длины а, Ь, с сторон, противолежащим соответствующимвершинам , найти радиус-вектор r центра круга, вписанного вэтот треугольник.1 3 .44. Зная радиус-векторы r 1 , r 2 , r з вершин треугольникаАБС и его внутренние углы, найти радиус-вектор r основанияперпендикуляра, опущенного из вершины А на сторону ВС .1 3 .45 . Доказать, что отрезки прямых, соединяющих середины противоположных ребер тетраэдра, пересекаются в однойточке и делятся этой точкой пополам .
Доказать также, что в тойже точке пересекаются отрезки прямых, соединяющих вершинытетраэдра с точками пересечения медиан противоположных граней, и делятся этой точкой в отношении 3 : 1 ( считая от вер:µ:rин) .1 3 .46. Доказать, что каково бы ни было конечное множество точек А 1 , А 2 , . . .
, А п (на прямой, на плоско сти или в пространстве) , существует и притом только одна такая точка М , чтоМА 1 + МА 2 + . . . + МА п = О.§ 14.Вещественное линейное пространствоНепустое множество V называется вещественнuм линеuн’Ым простrюнством, если на нем заданы два закона композиции:внутренний закон композиции, называемый сложением и подчиненныйаксиомам:1) а + Ь = Ь + а, Va, Ь Е ( аксиома коммутативности ) ,2) (а + Ь) + с = а + (Ь + с) , Va, Ь, с Е V ( аксиома ассоциативности ) ,3) () Е : а + () = а, Va ЕV3 VV,Глава IV. Введение в теорию линейных пространств1 264) V a E V 3 ( — a ) E V : a + ( — a ) = B ;внешний закон композиции, называемый умножением элемента а на число а Е IR и подчиненный аксиомам:5) 1 · а == а, /а Е V ,6) (оJЗ) а == а ({За) , Va, f3 Е IR, /а Е V ;и если эти законы связаны между собойаксиомами:7) ( а + {З) а = аа + {З а , /а, {3 Е IR , Va Е V (аксиома дистрибутивностиумножения на число относительно сложения чисел) ,8) а ( а + Ь) == аа + аЬ, Va Е IR, /а, Ь Е V (аксиома дистрибутивностиумножения на число относительно сложения элементов V ) .Элементы линейного пространства называются векторами, а само линейное пространство называют также векторнъш простIJанством.Вектор () называется нулевъш вектором пространства, а вектор ( -а ) противоположнъtм к вектору а .