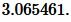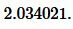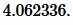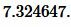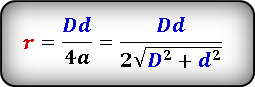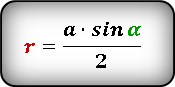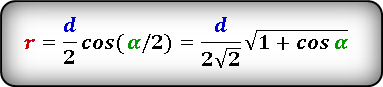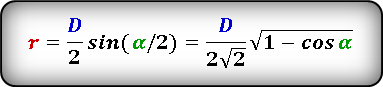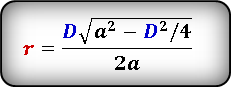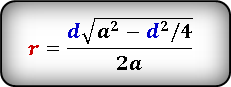Как найти радиус угла формула

Углы, связанные с окружностью

Вписанные и центральные углы

Определение 1 . Центральным углом называют угол, вершина которого совпадает с центром окружности, а стороны являются радиусами радиусами (рис. 1).

Определение 2 . Вписанным углом называют угол, вершина которого лежит на окружности, а стороны являются хордами хордами (рис. 2).

Напомним, что углы можно измерять в градусах и в радианах. Дуги окружности также можно измерять в градусах и в радианах, что вытекает из следующего определения.

Определение 3 . Угловой мерой (угловой величиной) дуги окружности является величина центрального угла, опирающегося на эту дугу.

Теоремы о вписанных и центральных углах

Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу.

Середина гипотенузы прямоугольного треугольника является центром описанной
около этого треугольника окружности.

Фигура	Рисунок	Теорема
Вписанный угол
Вписанный угол		Вписанные углы, опирающиеся на одну и ту же дугу равны.
Вписанный угол		Вписанные углы, опирающиеся на одну и ту же хорду, равны, если их вершины лежат по одну сторону от этой хорды
Вписанный угол		Два вписанных угла, опирающихся на одну и ту же хорду, в сумме составляют 180° , если их вершины лежат по разные стороны от этой хорды
Вписанный угол		Вписанный угол является прямым углом, тогда и только тогда, когда он опирается на диаметр
Окружность, описанная около прямоугольного треугольника

Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу.

Вписанные углы, опирающиеся на одну и ту же дугу равны.

Вписанные углы, опирающиеся на одну и ту же хорду, равны, если их вершины лежат по одну сторону от этой хорды

Два вписанных угла, опирающихся на одну и ту же хорду, в сумме составляют 180° , если их вершины лежат по разные стороны от этой хорды

Вписанный угол является прямым углом, тогда и только тогда, когда он опирается на диаметр

Середина гипотенузы прямоугольного треугольника является центром описанной
около этого треугольника окружности.

Теоремы об углах, образованных хордами, касательными и секущими

Величина угла, образованного пересекающимися хордами, равна половине суммы величин дуг, заключённых между его сторонами.

Величина угла, образованного секущими, пересекающимися вне круга, равна половине разности величин дуг, заключённых между его сторонами

Величина угла, образованного касательной и хордой, проходящей через точку касания, равна половине величины дуги, заключённой между его сторонами

Величина угла, образованного касательной и секущей, равна половине разности величин дуг, заключённых между его сторонами

Величина угла, образованного двумя касательными к окружности, равна половине разности величин дуг, заключённых между его сторонами

Фигура	Рисунок	Теорема	Формула
Угол, образованный пересекающимися хордами
Угол, образованный секущими, которые пересекаются вне круга
Угол, образованный касательной и хордой, проходящей через точку касания
Угол, образованный касательной и секущей
Угол, образованный двумя касательными к окружности

Величина угла, образованного пересекающимися хордами, равна половине суммы величин дуг, заключённых между его сторонами.

Величина угла, образованного касательной и хордой, проходящей через точку касания, равна половине величины дуги, заключённой между его сторонами

Угол, образованный пересекающимися хордами хордами

Формула:

Угол, образованный секущими секущими , которые пересекаются вне круга

Формула:

Величина угла, образованного секущими, пересекающимися вне круга, равна половине разности величин дуг, заключённых между его сторонами

Угол, образованный касательной и хордой хордой , проходящей через точку касания

Формула:

Угол, образованный касательной и секущей касательной и секущей

Формула:

Величина угла, образованного касательной и секущей, равна половине разности величин дуг, заключённых между его сторонами

Угол, образованный двумя касательными касательными к окружности

Формулы:

Величина угла, образованного двумя касательными к окружности, равна половине разности величин дуг, заключённых между его сторонами Доказательства теорем об углах, связанных с окружностью Теорема 1 . Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу. Доказательство . Рассмотрим сначала вписанный угол ABC , сторона BC которого является диаметром окружности диаметром окружности , и центральный угол AOC (рис. 5). Таким образом, в случае, когда одна из сторон вписанного угла проходит через центр окружности, теорема 1 доказана. Теперь рассмотрим случай, когда центр окружности лежит внутри вписанного угла (рис. 6). В этом случае справедливы равенства и теорема 1 в этом случае доказана. Осталось рассмотреть случай, когда центр окружности лежит вне вписанного угла (рис. 7). В этом случае справедливы равенства что и завершает доказательство теоремы 1. Теорема 2 . Величина угла, образованного пересекающимися хордами хордами , равна половине суммы величин дуг, заключённых между его сторонами. Доказательство . Рассмотрим рисунок 8. Нас интересует величина угла AED , образованного пересекающимися в точке E хордами AB и CD . Поскольку угол AED – внешний угол треугольника BED , а углы CDB и ABD являются вписанными углами, то справедливы равенства что и требовалось доказать. Теорема 3 . Величина угла, образованного секущими секущими , пересекающимися вне круга, равна половине разности величин дуг, заключённых между сторонами этого угла. Доказательство . Рассмотрим рисунок 9. Нас интересует величина угла BED , образованного пересекающимися в точке E секущими AB и CD . Поскольку угол ADC – внешний угол треугольника ADE , а углы ADC , DCB и DAB являются вписанными углами, то справедливы равенства что и требовалось доказать. Теорема 4 . Величина угла, образованного касательной и хордой касательной и хордой , проходящей через точку касания, равна половине величины дуги, заключённой между его сторонами. Доказательство . Рассмотрим рисунок 10. Нас интересует величина угла BAC , образованного касательной AB и хордой AC . Поскольку AD – диаметр диаметр , проходящий через точку касания, а угол ACD – вписанный угол, опирающийся на диаметр, то углы DAB и DCA – прямые. Поэтому справедливы равенства что и требовалось доказать Теорема 5 . Величина угла, образованного касательной и секущей касательной и секущей , равна половине разности величин дуг, заключённых между сторонами этого угла. Доказательство . Рассмотрим рисунок 11. Нас интересует величина угла BED , образованного касательной AB и секущей CD . Заметим, что угол BDC – внешний угол треугольника DBE , а углы BDC и BCD являются вписанными углами. Кроме того, углы DBE и DCB , в силу теоремы 4, равны. Поэтому справедливы равенства что и требовалось доказать. Теорема 6 .Величина угла, образованного двумя касательными к окружности касательными к окружности , равна половине разности величин дуг, заключённых между его сторонами. Доказательство . Рассмотрим рисунок 12. Нас интересует величина угла BED , образованного касательными AB и CD . Заметим, что углы BOD и BED в сумме составляют π радиан. Поэтому справедливо равенство Теорема синусов О чем эта статья: Статья находится на проверке у методистов Skysmart. Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана). Доказательство теоремы синусов Теорема синусов звучит так: стороны треугольника пропорциональны синусам противолежащих углов. Нарисуем стандартный треугольник и запишем теорему формулой: Формула теоремы синусов: Докажем теорему с помощью формулы площади треугольника через синус его угла. Из этой формулы мы получаем два соотношения: На b сокращаем, синусы переносим в знаменатели: bc sinα = ca sinβ Из этих двух соотношений получаем: Теорема синусов для треугольника доказана. Эта теорема пригодится, чтобы найти: Стороны треугольника, если даны два угла и одна сторона. Углы треугольника, если даны две стороны и один прилежащий угол. Доказательство следствия из теоремы синусов У теоремы синусов есть важное следствие. Нарисуем треугольник, опишем вокруг него окружность и рассмотрим следствие через радиус. где R — радиус описанной около треугольника окружности. Так образовались три формулы радиуса описанной окружности: Основной смысл следствия из теоремы синусов заключен в этой формуле: Радиус описанной окружности не зависит от углов α, β, γ. Удвоенный радиус описанной окружности равен отношению стороны треугольника к синусу противолежащего угла. Для доказательства следствия теоремы синусов рассмотрим три случая. 1. Угол ∠А = α — острый в треугольнике АВС. Проведем диаметр BA1. В этом случае точка А и точка А1 лежат в одной полуплоскости от прямой ВС. Используем теорему о вписанном угле и видим, что ∠А = ∠А1 = α. Треугольник BA1C — прямоугольный, в нём ∠ BCA1 = 90°, так как он опирается на диаметр BA1. Чтобы найти катет a в треугольнике BA1C, нужно умножить гипотенузу BA1 на синус противолежащего угла. BA1 = 2R, где R — радиус окружности Следовательно: R = α/2 sinα Для острого треугольника с описанной окружностью теорема доказана. 2. Угол ∠А = α — тупой в треугольнике АВС. Проведем диаметр окружности BA1. Точки А и A1 по разные стороны от прямой ВС. Четырёхугольник ACA1B вписан в окружность, и его основное свойство в том, что сумма противолежащих углов равна 180°. Следовательно, ∠А1 = 180° — α. Вспомним свойство вписанного в окружность четырёхугольника: Также известно, что sin(180° — α) = sinα. В треугольнике BCA1 угол при вершине С равен 90°, потому что он опирается на диаметр. Следовательно, катет а мы находим таким образом: α = 2R sin (180° — α) = 2R sinα Следовательно: R = α/2 sinα Для тупого треугольника с описанной окружностью теорема доказана. Часто используемые тупые углы: sin120° = sin(180° — 60°) = sin60° = 3/√2; sin150° = sin(180° — 30°) = sin30° = 1/2; sin135° = sin(180° — 45°) = sin45° = 2/√2. 3. Угол ∠А = 90°. В прямоугольнике АВС угол А прямой, а противоположная сторона BC = α = 2R, где R — это радиус описанной окружности. Для прямоугольного треугольника с описанной окружностью теорема доказана. Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курсы по профильной математике. Теорема о вписанном в окружность угле Из теоремы синусов и ее следствия можно сделать любопытный вывод: если известна одна сторона треугольника и синус противолежащего угла — можно найти и радиус описанной окружности. Но треугольник не задаётся только этими величинами. Это значит, что если треугольник еще не задан, найти радиус описанной окружности возможно. Раскроем эту тему на примере теоремы о вписанном в окружность угле и следствиях из нее. Теорема о вписанном угле: вписанный в окружность угол измеряется половиной дуги, на которую он опирается. ∠А = α опирается на дугу ВС. Дуга ВС содержит столько же градусов, сколько ее центральный угол ∠BOC. Формула теоремы о вписанном угле: Следствие 1 из теоремы о вписанном в окружность угле Вписанные углы, опирающиеся на одну дугу, равны. ∠А = ∠BAC опирается на дугу ВС. Поэтому ∠A = 1/2(∠COB). Если мы возьмём точки A1, А2. Аn и проведём от них лучи, которые опираются на одну и ту же дугу, то получим: На рисунке изображено множество треугольников, у которых есть общая сторона СВ и одинаковый противолежащий угол. Треугольники являются подобными, и их объединяет одинаковый радиус описанной окружности. Следствие 2 из теоремы о вписанном в окружность угле Вписанные углы, которые опираются на диаметр, равны 90°, то есть прямые. ВС — диаметр описанной окружности, следовательно ∠COB = 180°. Следствие 3 из теоремы о вписанном в окружность угле Сумма противоположных углов вписанного в окружность четырёхугольника равна 180°. Это значит, что: Угол ∠А = α опирается на дугу DCB. Поэтому DCB = 2α по теореме о вписанном угле. Угол ∠С = γ опирается на дугу DAB. Поэтому DAB = 2γ. Но так как 2α и 2γ — это вся окружность, то 2α + 2γ = 360°. Следовательно: α + γ = 180°. Поэтому: ∠A + ∠C = 180°. Следствие 4 из теоремы о вписанном в окружность угле Синусы противоположных углов вписанного четырехугольника равны. То есть: sinγ = sin(180° — α) Так как sin(180° — α) = sinα, то sinγ = sin(180° — α) = sinα Примеры решения задач Теорема синусов и следствия из неё активно используются при решении задач. Рассмотрим несколько примеров, чтобы закрепить материал. Пример 1. В треугольнике ABC ∠A = 45°,∠C = 15°, BC = 4√6. Найти AC. Согласно теореме о сумме углов треугольника: ∠B = 180° — 45° — 15° = 120° Сторону AC найдем по теореме синусов: Пример 2. Гипотенуза и один из катетов прямоугольного треугольника равны 10 и 8 см. Найти угол, который расположен напротив данного катета. В этой статье мы узнали, что в прямоугольном треугольнике напротив гипотенузы располагается угол, равный 90°. Примем неизвестный угол за x. Тогда соотношение сторон выглядит так: Значит x = sin (4/5) ≈ 53,1°. Ответ: угол составляет примерно 53,1°. Запоминаем Обычная теорема: стороны треугольника пропорциональны синусам противолежащих углов. >

Расширенная теорема: в произвольном треугольнике справедливо следующее соотношение:

Геометрия. Урок 5. Окружность

Смотрите бесплатные видео-уроки на канале Ёжику Понятно.

Видео-уроки на канале Ёжику Понятно. Подпишись!

Содержание страницы:

• Определение окружности

• Отрезки в окружности

Определение окружности

Окружность – геометрическое место точек, равноудаленных от данной точки.

Эта точка называется центром окружности .

Отрезки в окружности

Радиус окружности R – отрезок, соединяющий центр окружности с точкой на окружности.

Хорда a – отрезок, соединяющий две точки на окружности.

Диаметр d – хорда, проходящая через центр окружности, он равен двум радиусам окружности ( d = 2 R ).

O A – радиус, D E – хорда, B C – диаметр.

Теорема 1:
Радиус, перпендикулярный хорде, делит пополам эту хорду и дугу, которую она стягивает.

Касательная к окружности – прямая, имеющая с окружностью одну общую точку.

Из одной точки, лежащей вне окружности, можно провести две касательные к данной окружности.

Теорема 2:
Отрезки касательных, проведенных из одной точки, равны ( A C = B C ).

Теорема 3:
Касательная перпендикулярна радиусу, проведенному к точке касания.

Дуга в окружности

Часть окружности, заключенная между двумя точками, называется дугой окружности .

Например, хорда A B стягивает две дуги: ∪ A M B и ∪ A L B .

Теорема 4:
Равные хорды стягивают равные дуги.

Если A B = C D , то ∪ A B = ∪ C D

Углы в окружности

В окружности существует два типа углов: центральные и вписанные.

Центральный угол – угол, вершина которого лежит в центре окружности.

∠ A O B – центральный.

Центральный угол равен градусной мере дуги, на которую он опирается . ∪ A B = ∠ A O B = α

Если провести диаметр, то он разобьёт окружность на две полуокружности. Градусная мера каждой полуокружности будет равна градусной мере развернутого угла, который на неё опирается.

Градусная мара всей окружности равна 360 ° .

Вписанный угол – угол, вершина которого лежит на окружности, а стороны пересекают окружность.

∠ A C B – вписанный.

Вписанный угол равен половине градусной меры дуги, на которую он опирается . ∠ A C B = ∪ A B 2 = α 2 ∪ A B = 2 ⋅ ∠ A C B = α

Теорема 5:
Вписанные углы, опирающиеся на одну и ту же дугу, равны .

∠ M A N = ∠ M B N = ∠ M C N = ∪ M N 2 = α 2

Теорема 6:
Вписанный угол, опирающийся на полуокружность (на диаметр), равен 90 ° .

∠ M A N = ∠ M B N = ∪ M N 2 = 180 ° 2 = 90 °

Длина окружности, длина дуги

Мы узнали, как измеряется градусная мера дуги окружности (она равна градусной мере центрального угла, который на нее опирается) и всей окружности целиком (градусная мера окружности равна 360 ° ). Теперь поговорим о том, что же такое длина дуги в окружности. Длина дуги – это значение, которое мы бы получили, если бы мерили дугу швейным сантиметром. Рассмотрим две окружности с разными радиусами, в каждой из которых построен центральный угол равный α .

Градусная мера дуги ∪ A B равна градусной мере дуги ∪ C D и равна α .

Но невооуруженным глазом видно, что длины дуг разные. Если градусная мера дуги окружности зависит только от величины центрального угла, который на неё опирается, то длина дуги окружности зависит ещё и от радиуса самой окружноси.

Длина окружности находится по формуле:

Длина дуги окружности , на которую опирается центральный угол α равна:

l α = π R 180 ∘ ⋅ α

Площадь круга и его частей

Теперь поговорим про площадь круга, площадь сектора и площадь сегмента.

Круг – часть пространства, которая находится внутри окружности.

Иными словами, окружность – это граница, а круг – это то, что внутри.

Примеры окружности в реальной жизни: велосипедное колесо, обруч, кольцо.

Примеры круга в реальной жизни: пицца, крышка от канализационного люка, плоская тарелка.

Площадь круга находится по формуле: S = π R 2

Сектор – это часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга.

Примеры сектора в реальной жизни: кусок пиццы, веер.

Площадь кругового сектора, ограниченного центральным углом α находится по формуле: S α = π R 2 360 ° ⋅ α

Сегмент – это часть круга, ограниченная дугой и хордой, стягивающей эту дугу.

Примеры сегмента в реальной жизни: мармелад “лимонная долька”, лук для стрельбы.

Чтобы найти площадь сегмента, нужно сперва вычислить площадь кругового сектора, который данный сегмент содержит, а потом вычесть площадь треугольника, который образован центральным углом и хордой.

S = π R 2 360 ° ⋅ α − 1 2 R 2 sin α

Теорема синусов

Если вокруг произвольного треугольника описана окружность, то её радиус можно найти при помощи теоремы синусов:

a sin ∠ A = b sin ∠ B = c sin ∠ C = 2 R Достаточно знать одну из сторон треугольника и синус угла, который напротив неё лежит. Из этих данных можно найти радиус описанной окружности.

Примеры решений заданий из ОГЭ

Модуль геометрия: задания, связанные с окружностями.

Радиус описанной окружности около треугольника онлайн

1. Радиус окружности описанной около треугольника, если известны три стороны треугольника

Пусть известны три стороны a, b, c треугольника. Найдем радиус описанной окружности около треугольника.

Площадь треугольника по трем сторонам a, b, c и радиусу R описанной окружности имеет вид:

откуда

Площадь треугольника по трем сторонам имеет вид:

где

Подставляя (2) в (1), получим формулу радиуса описанной окружности около треугольника:

где p вычисляется из формулы (3).

Пример 1. Известны три стороны треугольника: ( small a=6, b=5, c=4.5 ). Найти радиус окружности описанной около треугольника.

Решение. Для нахождения радиуса окружности описанной около треугольника воспользуемся формулой (4), где ( small р ) вычисляется из формулы (3).

Найдем p из (2):

Подставим значения a, b, c, p в (1):

Ответ:

2. Радиус окружности описанной около треугольника, если известны сторона a и противолежащий угол A

Пусть известны сторона a и противолежащий угол A. Найдем радиус описанной окружности около треугольника. Из расширенной теоремы синусов имеем:

Откуда:

Пример 2. Сторона треугольника равна: 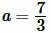а противолежащий угол ( small angle A=35°.) Найти радиус окружности описанной около треугольника.

Решение. Для нахождения радиуса окружности описанной около треугольника воспользуемся формулой (5). Подставим значения 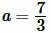и ( small angle A=35° ) в (5):

Ответ:

3. Радиус окружности описанной около треугольника, если известны стороны b и c треугольника и угол между ними A

Пусть известны стороны b и c треугольника и угол между ними A. Найдем радиус описанной окружности около треугольника.

Из теоремы косинусов, имеем:

или

Подставляя (6) в (5), получим требуемую формулу:

Пример 3. Известны две стороны треугольника: и угол между ними: ( small angle A=30°. ) Найти радиус окружности описанной около треугольника.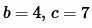

Решение. Для нахождения радиуса окружности описанной около треугольника воспользуемся формулой (7). Подставим значения 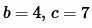и ( small angle A=30° ) в (7):

Ответ:

4. Радиус окружности описанной около треугольника, если известны сторона треугольника a и прилежащие углы B и C

Пусть известны сторона a треугольника и прилежащие к ней углы B и C. Найдем радиус описанной окружности около треугольника. Как известно, сумма углов треугольника равна 180°. Поэтому легко найти треий угол треугольника: ( small angle A=180°- (angle B+ nangle C). ) Тогда для нахождения радиуса описанной около треугольника окружности можно воспользоваться формулой (5):

Получили следующую формулу:

Пример 4. Известны сторона треугольника: и прилежащие к ней углы: ( small angle B=21°, ;angle C=34°. ) Найти радиус окружности описанной около треугольника.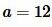

Решение. Для нахождения радиуса окружности описанной около треугольника воспользуемся формулой (8). Подставим значения 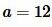и ( small angle B=21°, ;angle C=34° ) в (8):

Ответ:

Смотрите также:

• Радиус описанной окружности около равнобедренного треугольника онлайн
• Радиус описанной окружности около равностороннего треугольника онлайн
• Радиус описанной окружности около прямоугольного треугольника онлайн

1. Формулы радиуса вписанной окружности если известны: диагональ, стороны и угол

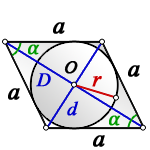
a — сторона ромба

D — большая диагональ

d — меньшая диагональ

α — острый угол

О — центр вписанной окружности

r — радиус вписанной окружности

Формула радиуса вписанной окружности в ромб через диагонали ( r ) :

Формула радиуса вписанной окружности в ромб через сторону и угол ( r ) :

Формула радиуса вписанной окружности в ромб через диагональ и угол ( r ) :

Формула радиуса вписанной окружности в ромб через диагональ и сторону ( r ) :

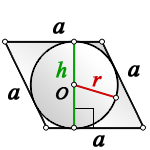
2. Радиус вписанной окружности ромба, равен половине его высоты

a — сторона ромба

h — высота

О — центр вписанной окружности

r — радиус вписанной окружности

Формула радиуса вписанной окружности в ромб ( r ) :

В данной публикации мы рассмотрим формулы, с помощью которых можно вычислить радиус окружности, описанной около произвольного (любого), прямоугольного или равностороннего треугольника. Также разберем примеры решения задач для закрепления представленного теоретического материала.

Формулы вычисления радиуса описанной окружности

Произвольный треугольник

Радиус окружности, описанной вокруг любого треугольника, рассчитывается по формуле:

где a, b, c – стороны треугольника, S – его площадь.

Прямоугольный треугольник

Радиус окружности, описанной около прямоугольного треугольника, равен половине его гипотенузы или высоте, проведенной к гипотенузе.

Равносторонний треугольник

Радиус описанной около правильного треугольника окружности вычисляется по формуле:

где a – сторона треугольника.

Примеры задач

Задание 1
Дан треугольник со сторонами 4, 6 и 9 см. Найдите радиус описанной около него окружности.

Решение
Для начала нам необходимо найти площадь треугольника. Т.к. нам известны длины всех его сторон, можно применить формулу Герона:

Теперь мы можем воспользоваться первой формулой из перечисленных выше для расчета радиуса круга:

Задание 2
Дан треугольник, у которого известны две стороны из трех: 6 и 8 см. Найдите радиус описанной вокруг него окружности.

Решение
Треугольник со сторонами 6 и 8 см может быть только прямоугольным, причем известные по условиям задачи стороны являются его катетами. Таким образом, мы можем найти гипотенузу фигуры, воспользовавшись теоремой Пифагора:

Как мы знаем, радиус круга, описанного вокруг прямоугольного треугольника, равняется половине его гипотенузы, следовательно: R = 10 : 2 = 5.

Радиус описанной около треугольника окружности

Обозначают данную геометрическую фигуру символом △.

Точками A, B и C обычно обозначают вершины треугольника. Отрезки AB, BC и AC определяют стороны треугольника, которые, как правило, обозначают с помощью латинской буквы. К примеру, AB = a, BC = b, AC = c.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Внутренность треугольника представляет собой часть плоскости, которая ограничена сторонами треугольника. Стороны треугольника в вершинах формируют три угла, которые обычно обозначают, используя греческие буквы – (alpha, beta, gamma) и другие. По этой причине треугольник получил название многоугольника с тремя углами. Для обозначения углов также применяют символ ∠, к примеру:

• (alpha )∠BAC или ∠CAB;
• (beta) ∠ABC или ∠CBA;
• (gamma )∠ACB или ∠BCA.

Треугольники различают по величине углов или количеству равных сторон:

• остроугольный, в котором все три угла острые, то есть меньше (90^{0});
• тупоугольный, обладает один из углов больше (90^{0}), а два остальных угла являются острыми;
• прямоугольный с одним прямым углом в (90^{0}), двумя сторонами, образующими прямой угол, которые называют катетами, третьей стороной, расположенной напротив прямого угла в виде гипотенузы;
• разносторонний, со сторонами разной длины;
• равнобедренный, с двумя одинаковыми боковыми сторонами и третьей стороной в виде основания, углы при котором равны;
• равносторонний (правильный) обладает тремя сторонами с одинаковой длиной и углами, равными по (60^{0}).

Радиус окружности, описанной около треугольника, определяется с помощью специальных формул, подкрепленных соответствующими доказательствами. Первая закономерность позволяет рассчитать его согласно расширенной теореме синусов: 

• радиус R окружности, описанной около треугольника, равен отношению стороны треугольника к удвоенному синусу противолежащего угла.

Формула для нахождения радиуса:

(R=frac{AB}{2sin angle C} =frac{AC}{2sin angle B} =frac{BC}{2sin angle A})

Вторую формулу для определения радиуса описанной около треугольника окружности записывают таким образом:

(R=frac{AB*BC*AC}{4S_{ABC}})

Общий вид:

(R=frac{abc}{4S})

Таким образом, для определения радиуса окружности, которая описана около треугольника, требуется произведение длины сторон этой геометрической фигуры разделить на четыре площади треугольника.

Площадь треугольника можно рассчитать, используя формулу Герона:

(S=sqrt{p(p-a)(p-b)(p-c)})

В данном случае р обозначает полупериметр и определяется по формуле:

(p=frac{a+b+c}{2})

В результате преобразованная формула для определения радиуса описанной около треугольника окружности примет следующий вид:

(R=frac{abc}{4sqrt{p(p-a)(p-b)(p-c)}})

Представленные закономерности справедливы в случае любого треугольника, независимо от его вида. При расчетах необходимо учитывать расположение центра описанной окружности.

Расположение центра окружности, описанной около треугольника:

• остроугольный треугольник – во внутренней области;
• прямоугольный треугольник – на середине гипотенузы;
• тупоугольный треугольник – вне геометрической фигуры, напротив тупого угла.

Вычисление радиуса через стороны

Выше были рассмотрены формулы, с помощью которых можно определить радиус окружности, описанной вокруг треугольника, зная его стороны. Кроме того, при решении задач можно использовать некоторые закономерности, предусмотренные для треугольников определенного типа.

Формула для равнобедренного треугольника

Обладая информацией о длине сторон равнобедренного треугольника, можно определить радиус окружности, описанной вокруг этого треугольника.

(R=frac{a^{2}}{sqrt{4a^{2}-b^{2}}})

где a и b являются сторонами треугольника.  

Формула для равностороннего треугольника

Такое выражение подходит для расчета радиуса окружности, описанной около любого правильного многоугольника. Формула имеет вид:

(R=frac{a}{2sin frac{180^{0}}{n}})

Здесь а является длиной стороны многоугольника, n – определяет количество его сторон.

Частным случаем правильного многоугольника является правильный треугольник. Тогда данную формулу можно применить для расчета радиуса окружности, описанной около правильного треугольника.

Формула радиуса описанной окружности для правильного треугольника:

(R=frac{a}{sqrt{3}})

Исключая иррациональность в знаменателе, получим:

(R=frac{asqrt{3}}{3})

Следует заметить, что в случае правильного треугольника радиус описанной окружности в два раза превышает радиус вписанной окружности:

R=2r

Формула для произвольного треугольника

Как правило, при решении задач по геометрии необходимо вычислить радиус окружности, описанной около произвольного треугольника. В этом случае целесообразно воспользоваться формулой:

(R=frac{abc}{4S})

Справедливо следующее равенство:

(R=frac{a}{2sin alpha }=frac{b}{2sin beta }= frac{c}{2sin gamma })

где a, b, c являются длинами сторон треугольника, (alpha, beta, gamma) определяются, как противолежащие этим сторонам углы, S представляет собой площадь треугольника.

Формула для прямоугольного треугольника

Радиус описанной около прямоугольного треугольника окружности можно определить по формуле:

(R=frac{AB}{2})

Таким образом, в случае прямоугольного треугольника радиус окружности, которая описана около него, равен половине гипотенузы. Как правило, ее обозначают с помощью «с», то есть АВ = с. Поэтому формула принимает следующий вид:

(R=frac{c}{2})

Примеры решения задач

Задача 1

Стороны треугольника равны 4, 6 и 9 см. Необходимо определить радиус окружности, которая описана около данного треугольника.

Решение

В первую очередь нужно рассчитать площадь рассматриваемого треугольника. Зная длины его сторон, ее можно определить с помощью формулы Герона:

(S=sqrt{9.5(9.5-4)*(9.5-6)*(9.5-9)}approx 9.56)

Затем достаточно просто найти радиус окружности:

(R=frac{4*6*9}{4*9.56}approx 5.65)

Ответ: радиус окружности равен 5.65 см

Задача 2

Известно, что катеты прямоугольного треугольника равны 6 и 8 см. Требуется рассчитать радиус окружности, которая описана около данного треугольника.

Решение

Определим гипотенузу рассматриваемого треугольника с помощью теоремы Пифагора:

(c=sqrt{6^{2}+8^{2}}=10)

Известно, что радиус окружности, которая описана около прямоугольного треугольника, соответствует половине его гипотенузы. Таким образом:

(R = 10/2 = 5)

Ответ: радиус окружности равен 5 см.

Задача 3

Необходимо определить радиус описанной окружности около треугольника АВС, стороны которого равны (AB=4sqrt{2}) см,( AC=7 см) и (angle A=45^{circ}.)

Решение

Определить радиус окружности, которая описана около треугольника, можно, как отношение произведения сторон треугольника к его площади, умноженной на 4:

(R=frac{ABcdot BCcdot AC}{4S} )

По теореме косинусов следует рассчитать сторону ВС:

(BC=sqrt{AC^2 +AB^2 -2ACcdot ABcdot cos angle A} =)

(=sqrt{49+32-2cdot 7cdot 4sqrt{2} cdot frac{sqrt{2} }2 } =sqrt{25} =5 cm)

Затем можно определить площадь треугольника АВС:

(S_{ABC} =frac{1}{2} cdot ABcdot ACcdot sin angle A=14 cm^2 )

Зная площадь, легко рассчитать радиус окружности:

(R=frac{ABcdot BCcdot AC}{4S} =frac{4sqrt{2} cdot 5cdot 7}{4cdot 14} =frac{5sqrt{2} }{2} cm)

Ответ: радиус окружности равен (frac{5sqrt{2} }2 см.)

Задача 4

Дан треугольник АВС со сторонами AB=3 см,( AC=sqrt{6} см). Необходимо определить углы этой геометрической фигуры. При этом радиус описанной окружности равен (R=sqrt{3}) см.

Решение

Согласно формуле, радиус описанной окружности равен отношению стороны треугольника к удвоенному синусу противолежащего угла:

(R=frac{AB}{2sin angle C} =frac{AC}{2sin angle B} =frac{BC}{2sin angle A} )

Таким образом, можно вычислить синусы углов треугольника:

(sin angle C=frac{AB}{2R} =frac{3}{2sqrt{3} } =frac{sqrt{3} }{2}, откуда angle C=60^{circ},)

(sin angle B=frac{AC}{2R} =frac{sqrt{6} }{2sqrt{3} } =frac{sqrt{2} }{2}, откуда angle B=45^{circ}.)

Далее следует определить угол А:

(angle A=180^{circ} -60^{circ} -45^{circ} =75^{circ} )

Ответ: (angle A=75^{circ} , angle B=45^{circ} , angle C=60^{circ})