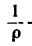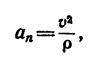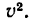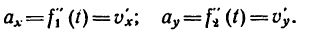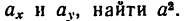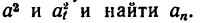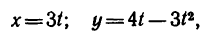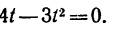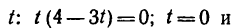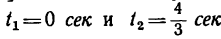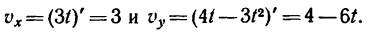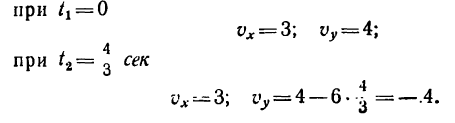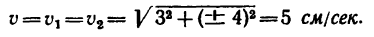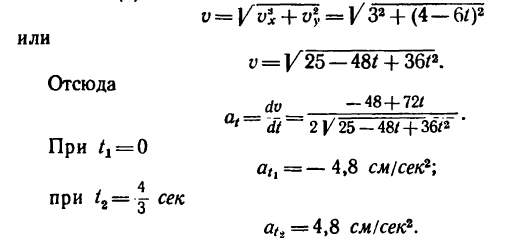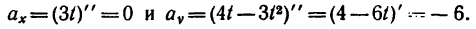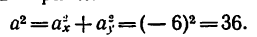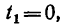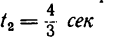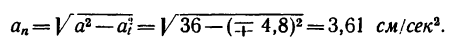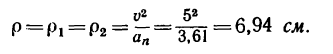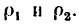Радиус кривизны траектории
В этой статье приведены две задачи, которые помогут вам научиться определять радиус кривизны траектории при движении тела под углом к горизонту. Каждая из задач представляет собой целый набор, поэтому неясностей не должно остаться.
Задача 1.
Тело брошено со скоростью 10 м/с под углом 
к горизонту. Найти радиусы кривизны траектории тела в начальный момент его движения, спустя время 0,5 с и в точке наивысшего подъема тела над поверхностью земли.
Как известно, радиус кривизны траектории связан с нормальным ускорением и скоростью формулой:
Откуда :
То есть, чтобы найти радиус кривизны траектории в любой точке, необходимо лишь знать скорость и нормальное ускорение, то есть ускорение, перпендикулярное вектору скорости. Рассмотрим все заданные точки и определим в них скорости и нужные составляющие ускорения.
К задаче 1
Самое простое – это определение этих величин в точке наивысшего подъема. Действительно, вертикальная составляющая скорости здесь равна нулю, поэтому скорость тела в данной точке равна горизонтальной составляющей, а ускорение, нормальное к вектору этой скорости – это ускорение свободного падения, поэтому
Вторая по простоте расчета – точка начала движения. Скорость в ней нам уже известна, осталось с ускорением разобраться. Ускорение свободного падения разложим на две составляющие: и . Первая – перпендикулярна скорости, она-то нам и нужна. Определяем радиус:
Наконец, точка, в которой тело окажется через пол-секунды.
Наше тело будет лететь по горизонтали с постоянной скоростью, равной . По вертикали тело будет двигаться равнозамедленно до середины траектории (наивысшей точки), а затем равноускоренно. Определим, успеет ли тело добраться до апогея:
Простой прикидочный расчет показывает, что нужная нам точка находится на первой половине траектории, где тело еще двигается вверх. Тогда его скорость по оси :
Определим полную скорость тела в момент времени :
Угол наклона вектора скорости к горизонту в этот момент равен:
А можно было сразу и косинус найти:
Тогда искомый радиус кривизны траектории равен:
Ответ: м, м, м.
Задача 2.
Под каким углом к горизонту нужно бросить шарик, чтобы а) радиус кривизны траектории в начальный момент времени был в 8 раз больше, чем в вершине; б) центр кривизны вершины траектории находился бы на поверхности земли?
Запишем условие задачи так: а) , б).
а)Как и в предыдущей задаче, определяем радиус кривизны траектории в точке броска. Скорость нам известна, а нормальным ускорением будет проекция ускорения свободного падения:
Определим теперь радиус кривизны в вершине:
По условию :
б) Мы уже определили , осталась максимальная высота подъема.
Время определяем из условия равенства нулю вертикальной составляющей скорости так же, как мы это делали в предыдущей задаче:
Приравниваем и :
Откуда .
Ответ: а) , б) .
2 комментария
Есин из Хотам и ПВ
✉️
17.02.2022 15:20:44
Thank you very much
Jahongir
✉️
12.04.2022 19:14:12
Спасибо огромное! Полностью разобрался 
Успехов вам!
Преподаватель который помогает студентам и школьникам в учёбе.
Кинематический способ определения радиуса кривизны траектории в теоретической механике
Кинематический способ определения радиуса кривизны траектории:
При решении многих технических задач возникает необходимость знать радиус кривизны р (или
Таким образом, если закон движения точки задан уравнениями 
то при определении радиуса кривизны траектории рекомендуется произвести следующее:
1. Продифференцировав уравнения движения, найти выражения проекций на оси координат вектора скорости:
2. Подставив в (б’) выражения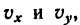 
найти 
3. Продифференцировав по t уравнение (б), полученное непосредственно из (б’), найти касательное ускорение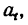 
а затем а?.
4. Продифференцировав вторично уравнения движения, найти выражения проекций на оси координат вектора ускорения
5. Подставив в (г) выражения 
6. Подставить в (в) значения
7. Подставив в (а) найденные значения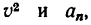 
получить радиус кривизны р.
Задача:
Движение точки задано уравнениями 
(х, у—в см, t — в сек). Определить радиус кривизны траектории в те моменты, когда она пересекает ось Ох.
Решение.
1. В те моменты, когда траектория пересекает ось Ох, ордината у—0. Поэтому, подставив во второе уравнение движения значение у = 0, получим
Отсюда [решая уравнение относительно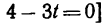 
находим, что траектория пересекает ось Ох в моменты времени
2. Находим выражения проекций скорости:
Как видно, проекция скорости на ось Ох — постоянная величина (не зависит от времени).
3. Определяем значение этих проекций в моменты пересечения траекторией оси Ох:
4. Числовое значение скорости точки в моменты пересечения траекторией оси Ох в данном случае одинаковы
5. Находим касательное ускорение точки. Для этого получим общее выражение (уравнение) скорости, воспользовавшись зависимостью (б):
6. Находим проекции полного ускорения точки:
Следовательно, в данном случае полное ускорение точки — постоянная величина. Причем
7. Определяем нормальное ускорение точки. Как при 
так и при 
8. Зная, что в моменты пересечения траекторией оси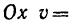 
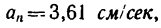
5 см:сек и 
находим радиусы кривизны траектории в этих точках:
Решение этой задачи рекомендуется самостоятельно иллюстрировать чертежом, изобразив на нем траекторию точки, векторы скорости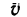 
и ускорения а в местах пересечения траектории с осью Ох (эти векторы легко построить при помощи найденных проекций), а также радиусы 
- Равномерное вращательное движение
- Равнопеременное вращательное движение
- Неравномерное вращательное движение
- Плоскопараллельное движение тела
- Равномерное криволинейное движение точки
- Равнопеременное движение точки
- Неравномерное движение точки по любой траектории
- Определение траектории, скорости и ускорения точки
Как найти радиус кривизны траектории
При рассмотрении движения тел используется ряд характеризующих величин, например тангенциальное и нормальное (центростремительное) ускорение, скорость, а также кривизна траектории. Радиус кривизны – геометрическое понятие, обозначающее радиус окружности R, по которой движется тело. Этот параметр можно найти по соответствующим формулам с помощью заданной траектории движения.
Инструкция
Наиболее часто встречаются задачи на определение радиуса кривизны траектории полета брошенного тела в заданный промежуток времени. Траектория движения в данном случае описывается уравнениями на координатных осях: х = f(t), y = f(t), где t – время, в момент которого требуется найти радиус. Его вычисление будет основываться на применении формулы аn = V²/R. Здесь радиус R выявляется из отношения нормального ускорения аn и мгновенной скорости V движения тела. Узнав данные величины, можно легко найти искомую компоненту R.
Вычислите проекции скорости тела на осях (ОХ, ОY). Математический смысл скорости – это первая производная от уравнения движения. Поэтому они легко находятся взятием производной от заданных уравнений: Vx = x’, Vy = y’. При рассмотрении геометрического отображения данных проекций в координатной системе видно, что они являются катетами прямоугольного треугольника. Причем гипотенуза в нем – искомая мгновенная скорость. Исходя из этого, вычислите величину мгновенной скорости V по теореме Пифагора: V = √( Vx² + Vy²). Подставляя в выражение известное значение времени, найдите числовой показатель V.
Модуль нормального ускорения также легко определить, рассмотрев другой прямоугольный треугольник, образуемый модулем полного ускорения а и касательного ускорения тела ак. Причем здесь нормальное ускорение является катетом и вычисляется так: аn = √( а² — ак²). Для нахождения касательного ускорения продифференцируйте по времени уравнение мгновенной скорости движения: ак = |dV/dt|. Полное же ускорение вычислите по его проекциям на оси, аналогично нахождению мгновенной скорости. Только для этого возьмите от заданных уравнений движения производные второго порядка: ах = х», аy = y». Модуль ускорения а = √( ах2 + аy2). Подставляя все найденные величины, определите числовое значение нормального ускорения аn = √( а² — ак²).
Выразите из формулы аn = V²/R искомую переменную радиуса кривизны траектории: R = V²/ аn. Подставьте числовые значения скорости и ускорения, вычислите радиус.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Движение
называют криволинейным, если скорость
м. т. изменяется и по величине, и по
направлению.
Одной
из основных характеристик этого движения
считается ускорение. В реальной жизни
чаще всего встречается криволинейное
движение, когда величина скорости –
остаётся постоянной, а направление
непрерывно изменяется. Например,
равномерное движение м. т. по окружности.
Рис.
14
Рассмотрим движение м. т.
вдоль произвольной кривой.
Из
математики известно, что малую часть
дуги любой плавной кривой (траектории)
можно заменить дугой окружности
некоторого радиуса R1
или R2
с центром в точке 01
или 02
(рис. 14).
Окружность,
которая в пределе совпадает с бесконечно
малой дугой произвольной кривой, называют
кругом кривизны.
Радиус
этой окружности называют радиусом
кривизны (R1
и
R2),
а центр окружности – центром кривизны
(т. 01
и т. 02,
рис. 14). Величину С =1/R называют кривизной
данной траектории.
1.19. Центростремительное, тангенциальное
и полное
ускорения
Пусть
в плоской системе координат (XOY)
движется м. т., описывая криволинейную
траекторию. В произвольный момент
времени t1
материальная
точка при движении со скоростью
находилась в пункте А. В следующий
момент времениt2
она находится в пункте В, имея скорость
(рис. 15). Если интервал времениt
мал, то участок криволинейной траектории
представляет собой некоторую дугу
АЕ, которая в пределе совпадает с дугой
некоторого круга кривизны радиуса R с
центром в точке 0. Скорости
и
отличаются и по величине, и по направлению,
т.
е.
иV1
V2
.
Рис.
15
Перенесём
вектор
(можно и вектор
)
параллельно самому себе так, чтобы
совпали начала векторов
и
в точке А.
Соединим
концы векторов
и
направленным отрезком ВД и обозначим
его
.
Вектор
является
вектором изменения (приращения) скорости
(рис. 15) за время t
и характеризует изменение скорости,
как по величине,
так
и по
направлению.
На
отрезке АВ (модуль вектора
)
отложим отрезок АС, равный по величине
модулю вектора
.
– хорда АЕ, следует, что
,
где
= vDt,
так как АС =
После преобразования
,
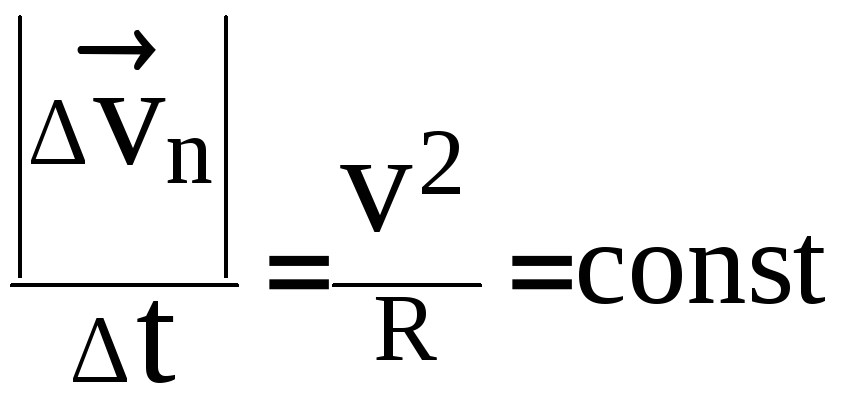
поскольку
R = const и
= сonst, так как вектор в квадрате есть
скаляр. В связи с тем, что изменение
скорости
произошло
за время Dt,
разделим левую и правую части на Dt:
.
По определению
мгновенного ускорения, имеем: слева
– вектор полного ускорения
справа – первое
слагаемоe
,
(34)
второе
слагаемое
(35)
Тогда
,
(36)
Рис.
16
,
(37)
т.
е. аn
=
v2/R,
(38)
где
– единичный вектор нормали.
Он
направлен по радиусу к центру круга
кривизны (рис.16), так как с переходом к
пределу, когда точки А и Е сливаются,
скорость
приближается к
и уголÐ
a
0 (рис.15).
Соответственно
углы АСД и АДC равны и стремятся к 90о.
Следовательно,
в пределе вектор
(
или
)
направлен по радиусу к центру круга
кривизны и называется
центростремительным (нормальным)
ускорением.
Вектор
центростремительного ускорения направлен
по радиусу к центру круга кривизны и
характеризует изменение скорости по
направлению. Рассмотрим
вторую составляющую полного ускорения.
Соединим
точки С и Д направленным отрезком,
который обозначим вектором
,
характеризующим изменение скорости
только понаправлению.
Направленный
отрезок ВС назовем вектором
,
характеризующим изменение скорости по
величине,
т. е.
.
Согласно
рис. 15,
.
(33)
Из подобия
равнобедренных треугольников ОАЕ и
АСД, где модуль
Вектор
(39)
называют
тангенциальным
(касательным) ускорением,
где
– единичный вектор, направленный по
касательной к траектории, т. е.
(
)
,
Вектор касательного
ускорения характеризует изменение
скорости по величине, направлен по
касательной к траектории в данной точке.
При
произвольном криволинейном движении
материальной точки полное ускорение
может быть разложено на две составляющие:
,
где
.
Вектор
полного ускорения характеризует
изменение скорости по величине и
направлению, направлен внутрь кривизны
траектории.
Модуль полного
ускорения
.
(40)
Возникновение
нормального и тангенциального ускорений
наблюдается, например, при движении
искусственных спутников Земли.