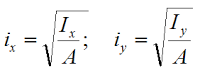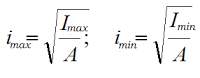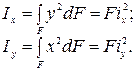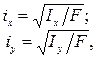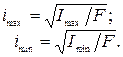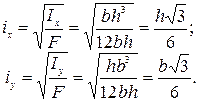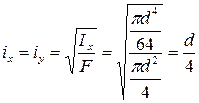Что такое радиус инерции сечения
Надежда Сторчай
Эксперт по предмету «Архитектура и строительство»
Задать вопрос автору статьи
Понятие радиуса инерции
Радиус инерции – это геометрическая характеристика сечения, которая связывает площадь плоской фигуры и её момент инерции.
Рисунок 1. Формула. Автор24 — интернет-биржа студенческих работ
Из формулы момента инерции относительно оси z можно выразить радиус инерции:
Рисунок 2. Формула. Автор24 — интернет-биржа студенческих работ
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Отсюда следует, что радиус инерции включает в себя изгибную жесткость стержня EJ и жесткость данного элемента на сжатие EF.
Радиус инерции можно вычислить для любых геометрических фигур:
- прямоугольных;
- круглых;
- треугольных;
- составных;
- произвольной формы.
Влияние радиуса инерции на характеристики элементов
При потере устойчивости стержня в результате сжатия в сопротивлении элемента продольному изгибу основную роль будет играть гибкость стержня. Поскольку наименьший радиус инерции сечения неразрывно связан с гибкостью, справедливо будет утверждать, что он в такой же степени влияет на сопротивление стержня продольному изгибу.
Это может говорить о том, что наиболее экономичным будет такое сечение, у которого минимальный радиус инерции будет равен наибольшему.
В международной системе СИ единица измерения радиуса инерции – м. В строительных источниках он чаще всего записывается в миллиметрах или сантиметрах ввиду небольшой величины.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Дата последнего обновления статьи: 09.09.2022
Моментом инерции
твердого тела относительно какой –
либо осиz
(осевым моментом инерции) называется
скалярная величина, равная сумме,
составленной из произведений массы mk
каждой точки тела на квадрат ее расстояния
rk
до данной оси.
Момент инерции
бесконечно тонкого кольца (материальной
окружности) относительно его оси вращения
равен произведению его массы на квадрат
радиуса:
Момент инерции
тела относительно оси представить в
виде произведения массы тела на квадрат
длины некоторого отрезка
,
называемого радиусом инерции тела
относительно соответствующей оси:
Под радиусом инерции
тела относительно какой – либо оси
можно понимать радиус такого бесконечно
тонкого кольца, в котором нужно
сосредоточить всю массу М тела, чтобы
получить момент инерции кольца, равный
моменту инерции тела относительно этой
оси.
10. Момент инерции относительно параллельных осей (теорема Гюйгенса — Штейна).
Момент инерции
тела относительно какой – либо оси
равен моменту инерции этого тела
относительно центральной оси, параллельной
данной оси, сложенному с произведением
массы тела на квадрат расстояния между
этими осями.
— теорема Гюйгенса
– Штейна.
11. Осевые моменты инерции однородных тел: стержень, полый и сплошной цилиндры, шар.
— момент инерции
тонкого прямого стержня постоянного
сечения
Момент инерции
однородного прямого тонкого стержня
относительно его центральной оси
симметрии равен 1/12 произведения массы
стержня на квадрат его длины.
— момент инерции
сплошного
круглого цилиндра.
Момент инерции
однородного сплошного круглого цилиндра
относительно его оси вращения равен
половине произведения массы цилиндра
на квадрат его радиуса.
— момент инерции
полого круглого цилиндра.
Момент инерции
однородного полого круглого цилиндра
относительно его оси вращения равен
половине произведения массы цилиндра
на сумму квадратов его наружного и
внутреннего радиусов.
12. Динамическое уравнение вращения твердого тела вокруг неподвижной оси.
(1), где
Произведение
момента инерции тела относительно его
оси вращения на угловое ускорение тела
равно главному моменту всех приложенных
к телу внешних сил относительно той же
оси.
Уравнение (1)
называется динамическим уравнением
вращательного движения твердого тела.
13. Теорема об изменении кинетической энергии материальной системы.
Изменение кинетической
энергии механической системы на некотором
перемещении равно сумме работ внешних
и внутренних сил, действующих на
материальные точки системы на этом
перемещении.
,
где Т – кинетическая энергия в конечный
момент времени
Т0
— кинетическая энергия в начальный
момент времени
∑Аiе
+∑Аij
– сумма работ внешних и внутренних сил
Условие: необходимо
начальное и конечное положения.
14. Кинетическая энергия материальной системы. Теорема Кенига.
Механическая
система – совокупность тел, связанных
между собой различными связями.
Положения и движение
каждого из тел взаимно обусловлено.
Кинетическая энергия механической
системы определяется как арифметическая
сумма кинетических энергий i-го
тела, входящего в систему.
Теорема Кенига:
Кинетическая
энергия механической системы равна
сумме кинетической энергии центра масс
системы, масса которого равна массе
всей системы, и кинетической энергии
этой системы в ее относительном движении
относительно центра масс.
Соседние файлы в папке Шпоры
- #
- #
- #
- #
- #
- #
Радиусом инерции i называют расстояние от соответствующей оси до точки, концентрация всей площади сечения в которой, даст такой же момент инерции, как и для всей площади рассматриваемой фигуры.
Отсюда:
Здесь:
A — площадь поперечного сечения;
Ix, Iy — осевые моменты инерции.
При расчете относительно главных осей сечения получаем главные радиусы инерции:
где Imax и Imin — соответственно максимальный и минимальный осевые моменты инерции фигуры.
Размерность — метр (либо кратные — см, мм).
Для стандартных прокатных профилей (например: двутавр или швеллер) значения радиусов инерции указаны в соответствующем сортаменте.
Понятие радиуса инерции часто используется в сопромате при расчетах на устойчивость и внецентренное нагружение.
Моменты инерции плоских сечений >
Примеры решения задач >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Решение задач и лекции по технической механике, теормеху и сопромату
Радиус инерции прямоугольного сечения (формула и расчет)
b — ширина сечения в мм; h — высота сечения в мм; y, z — центральные оси сечения.
Введите ширину сечения b в мм:
Введите высоту сечения h в мм:
В результате радиус инерции iy относительно центральной оси y равен:
0.00мм
0.00см
0.00м
В результате радиус инерции iz относительно центральной оси z равен:
0.00мм
0.00см
0.00м
Как найти радиус инерции прямоугольного сечения относительно его центральных осей?
Радиус инерции сечения относительно осей z и y можно рассчитать по формулам:
iy = h/√12 ≈ 0.288675 h,
iz = b/√12 ≈ 0.288675 b,,
где
iy — радиус инерции относительно центральной оси y в мм;
iz -радиус инерции относительно центральной оси z в мм ;
b — ширина сечения в мм (см. на рисунке вверху статьи);
h — высота сечения в мм (см. на рисунке вверху статьи).
Радиус инерции
Момент инерции фигуры относительно координатной оси может быть представлен в виде произведения площади фигуры на квадрат радиуса инерции:
Ввели в рассмотрение еще две геометрические характеристики: радиусы инерции поперечного сечения относительно осей x и y, соответственно. Формула радиуса инерции имеет вид:
Главным центральным осям инерции соответствуют главные радиусы инерции:
Для прямоугольника (см. рис. 4.4, а) главные радиусы инерции равны:
Для круглого сечения формула главных радиусов инерции имеет вид:
2