Как найти радиус спирали

From Wikipedia, the free encyclopedia

Three 360° loops of one arm of an Archimedean spiral

The Archimedean spiral (also known as the arithmetic spiral) is a spiral named after the 3rd-century BC Greek mathematician Archimedes. It is the locus corresponding to the locations over time of a point moving away from a fixed point with a constant speed along a line that rotates with constant angular velocity. Equivalently, in polar coordinates (r, θ) it can be described by the equation

with real numbers a and b. Changing the parameter a moves the centerpoint of the spiral outward from the origin (positive a toward θ = 0 and negative a toward θ = π) essentially through a rotation of the spiral, while b controls the distance between loops.

From the above equation, it can thus be stated: position of particle from point of start is proportional to angle θ as time elapses.

Archimedes described such a spiral in his book On Spirals. Conon of Samos was a friend of his and Pappus states that this spiral was discovered by Conon.^[1]

Derivation of general equation of spiral[edit]

A physical approach is used below to understand the notion of Archimedean spirals.

Suppose a point object moves in the Cartesian system with a constant velocity v directed parallel to the x-axis, with respect to the xy-plane. Let at time t = 0, the object was at an arbitrary point (c, 0, 0). If the xy plane rotates with a constant angular velocity ω about the z-axis, then the velocity of the point with respect to z-axis may be written as:

The xy plane rotates to an angle ωt (anticlockwise) about the origin in time t. (c, 0) is the position of the object at t = 0. P is the position of the object at time t, at a distance of R = vt + c.

${displaystyle {begin{aligned}|v_{0}|&={sqrt {v^{2}+omega ^{2}(vt+c)^{2}}}\v_{x}&=vcos omega t-omega (vt+c)sin omega t\v_{y}&=vsin omega t+omega (vt+c)cos omega tend{aligned}}}$

Here vt + c is the modulus of the position vector of the particle at any time t, v_x is the velocity component along the x-axis and v_y is the component along the y-axis. The figure shown alongside explains this.

${displaystyle {begin{aligned}int v_{x},dt&=x\int v_{y},dt&=yend{aligned}}}$

The above equations can be integrated by applying integration by parts, leading to the following parametric equations:

${displaystyle {begin{aligned}x&=(vt+c)cos omega t\y&=(vt+c)sin omega tend{aligned}}}$

Squaring the two equations and then adding (and some small alterations) results in the Cartesian equation

${displaystyle {sqrt {x^{2}+y^{2}}}={frac {v}{omega }}cdot arctan {frac {y}{x}}+c}$

(using the fact that ωt = θ and θ = arctan y/x) or

${displaystyle tan left(left({sqrt {x^{2}+y^{2}}}-cright)cdot {frac {omega }{v}}right)={frac {y}{x}}}$

Its polar form is

${displaystyle r={frac {v}{omega }}cdot theta +c.}$

Arc length and curvature [edit]

Osculating circles of the Archimedean spiral, tangent to the spiral and having the same curvature at the tangent point. The spiral itself is not drawn, but can be seen as the points where the circles are especially close to each other.

Given the parametrization in cartesian coordinates

the arc length from $theta _{1}$ to $theta _{2}$ is

${displaystyle {frac {b}{2}}left[theta ,{sqrt {1+theta ^{2}}}+ln left(theta +{sqrt {1+theta ^{2}}}right)right]_{theta _{1}}^{theta _{2}}}$

or, equivalently:

${displaystyle {frac {b}{2}}left[theta ,{sqrt {1+theta ^{2}}}+operatorname {arsinh} theta right]_{theta _{1}}^{theta _{2}}.}$

The total length from to ${displaystyle theta _{2}=theta }$ is therefore

${displaystyle {frac {b}{2}}left[theta ,{sqrt {1+theta ^{2}}}+ln left(theta +{sqrt {1+theta ^{2}}}right)right].}$

The curvature is given by

${displaystyle kappa ={frac {theta ^{2}+2}{b(theta ^{2}+1)^{frac {3}{2}}}}}$

Characteristics[edit]

Archimedean spiral represented on a polar graph

The Archimedean spiral has the property that any ray from the origin intersects successive turnings of the spiral in points with a constant separation distance (equal to 2πb if θ is measured in radians), hence the name «arithmetic spiral». In contrast to this, in a logarithmic spiral these distances, as well as the distances of the intersection points measured from the origin, form a geometric progression.

The Archimedean spiral has two arms, one for θ > 0 and one for θ < 0. The two arms are smoothly connected at the origin. Only one arm is shown on the accompanying graph. Taking the mirror image of this arm across the y-axis will yield the other arm.

For large θ a point moves with well-approximated uniform acceleration along the Archimedean spiral while the spiral corresponds to the locations over time of a point moving away from a fixed point with a constant speed along a line which rotates with constant angular velocity^[2] (see contribution from Mikhail Gaichenkov).

As the Archimedean spiral grows, its evolute asymptotically approaches a circle with radius |v|/ω.

General Archimedean spiral[edit]

Sometimes the term Archimedean spiral is used for the more general group of spirals

${displaystyle r=a+bcdot theta ^{frac {1}{c}}.}$

The normal Archimedean spiral occurs when c = 1. Other spirals falling into this group include the hyperbolic spiral (c = −1), Fermat’s spiral (c = 2), and the lituus (c = −2).

Applications[edit]

One method of squaring the circle, due to Archimedes, makes use of an Archimedean spiral. Archimedes also showed how the spiral can be used to trisect an angle. Both approaches relax the traditional limitations on the use of straightedge and compass in ancient Greek geometric proofs.^[3]

Mechanism of a scroll compressor

The Archimedean spiral has a variety of real-world applications. Scroll compressors, used for compressing gases, have rotors that can be made from two interleaved Archimedean spirals, involutes of a circle of the same size that almost resemble Archimedean spirals,^[4] or hybrid curves.

Archimedean spirals can be found in spiral antenna, which can be operated over a wide range of frequencies.

The coils of watch balance springs and the grooves of very early gramophone records form Archimedean spirals, making the grooves evenly spaced (although variable track spacing was later introduced to maximize the amount of music that could be cut onto a record).^[5]

Asking for a patient to draw an Archimedean spiral is a way of quantifying human tremor; this information helps in diagnosing neurological diseases.

Archimedean spirals are also used in digital light processing (DLP) projection systems to minimize the «rainbow effect», making it look as if multiple colors are displayed at the same time, when in reality red, green, and blue are being cycled extremely quickly.^[6] Additionally, Archimedean spirals are used in food microbiology to quantify bacterial concentration through a spiral platter.^[7]

They are also used to model the pattern that occurs in a roll of paper or tape of constant thickness wrapped around a cylinder.^[8]^[9]

Many dynamic spirals (such as the Parker spiral of the solar wind, or the pattern made by a Catherine’s wheel) are Archimedean. For instance, the star LL Pegasi shows an approximate Archimedean spiral in the dust clouds surrounding it, thought to be ejected matter from the star that has been shepherded into a spiral by another companion star as part of a double star system.^[10]

References[edit]

^ Bulmer-Thomas, Ivor. «Conon of Samos». Dictionary of Scientific Biography. Vol. 3. p. 391.
^ Sloane, N. J. A. (ed.). «Sequence A091154». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
^ Boyer, Carl B. (1968). A History of Mathematics. Princeton, New Jersey: Princeton University Press. pp. 140–142. ISBN 0-691-02391-3.
^ Sakata, Hirotsugu; Okuda, Masayuki. «Fluid compressing device having coaxial spiral members». Retrieved 2006-11-25.
^ Penndorf, Ron. «Early Development of the LP». Archived from the original on 5 November 2005. Retrieved 2005-11-25.. See the passage on Variable Groove.
^ Ballou, Glen (2008), Handbook for Sound Engineers, CRC Press, p. 1586, ISBN 9780240809694
^ Gilchrist, J. E.; Campbell, J. E.; Donnelly, C. B.; Peeler, J. T.; Delaney, J. M. (1973). «Spiral Plate Method for Bacterial Determination». Applied Microbiology. 25 (2): 244–52. doi:10.1128/AEM.25.2.244-252.1973. PMC 380780. PMID 4632851.
^ Peressini, Tony (3 February 2009). «Joan’s Paper Roll Problem» (PDF). Archived from the original (PDF) on 3 November 2013. Retrieved 2014-10-06.
^ Walser, H.; Hilton, P.; Pedersen, J. (2000). Symmetry. Mathematical Association of America. p. 27. ISBN 9780883855324. Retrieved 2014-10-06.
^ Kim, Hyosun; Trejo, Alfonso; Liu, Sheng-Yuan; Sahai, Raghvendra; Taam, Ronald E.; Morris, Mark R.; Hirano, Naomi; Hsieh, I-Ta (March 2017). «The large-scale nebular pattern of a superwind binary in an eccentric orbit». Nature Astronomy. 1 (3): 0060. arXiv:1704.00449. Bibcode:2017NatAs…1E..60K. doi:10.1038/s41550-017-0060. S2CID 119433782.

External links[edit]

Jonathan Matt making the Archimedean spiral interesting — Video : The surprising beauty of Mathematics — TedX Talks, Green Farms
Weisstein, Eric W. «Archimedes’ Spiral». MathWorld.
archimedean spiral at PlanetMath.
Page with Java application to interactively explore the Archimedean spiral and its related curves
Online exploration using JSXGraph (JavaScript)
Archimedean spiral at «mathcurve»

Источник

Спираль Архимеда

Опубликовано 02.05.2021

Спираль Архимеда – это линия, которая напоминает спираль и выражается определенным уравнением. Открытие кривой приписывается Конону Самосскому, ученику Архимеда. В честь его учителя – спираль названа спиралью Архимеда. Давайте же разберемся с этой линией и попробуем ее самостоятельно построить.

Спираль Архимеда

Линия, которую называют спиралью Архимеда, строится в полярных координатах и определяется уравнением:

Здесь – это положительное число, – полярный радиус.

Другие названия: равносторонняя спираль, неоид.

Как построить спираль Архимеда

Чтобы построить спираль Архимеда, нужно присваивать некоторые произвольные значения и определять . Построим таблицу значений:


0	0
$frac{pi}{2}$	$frac{pi}{2}a$

$frac{3pi}{2}$	$frac{3pi}{2}a$

Данная таблица показывает, что при возрастании угла в арифметической прогрессии с разностью $frac{pi}{2}$ полярный радиус возрастает тоже в арифметической прогрессии с разностью $a frac{pi}{2}$ . Кроме того, заметим, что всякой точке этой линии с положительными координатами соответствует на этой линии точка , то есть спираль Архимеда симметрично расположена относительно прямой, проходящей через полюс перпендикулярно к полярной оси.

На рисунке изображена спираль Архимеда – сплошной линией изображена ветвь, соответствующая положительным значениям , а пунктирной – отрицательным.

Благодаря этой спирали можно рассчитать площадь круга, по записям Архимед умел это делать и знал, что “поверхность первого витка спирали равна одной трети поверхности круга, радиус которого равен длине, пройденной точкой на прямой, во время рисования первого витка”.

Спираль Архимеда – это траектория точки, равномерно движущейся по прямой линии плоскости, причем эта линия равномерно поворачивается вокруг одной из своих точек.

Спираль Архимеда активно используется в искусстве, посмотрите:

Видео – как нарисовать спираль Архимеда

( 4 оценки, среднее 5 из 5 )

Источник

Спирали Архимеда широко используются при построении геометрий для катушек индуктивности, спиральных теплообменников и микрогидродинамических устройств. В этой заметке мы покажем, как построить спираль Архимеда, используя аналитические выражения и их производные для задания необходимых кривых. Сначала мы создадим двухмерную геометрию, а затем, задав нужную толщину, преобразуем её в трёхмерную с помощью операции Extrude (Вытягивание).

Что такое спираль Архимеда?

Широко распространённые в природе спирали или завитки используются во многих инженерных конструкциях. Например, в электротехнике и электронике с помощью проводников спиралевидной формы наматывают катушки индуктивности или проектируют геликоидные антенны. В машиностроении спирали используются при проектировании пружин, косозубых цилиндрических передач или даже механизмов часов, один из которых изображён ниже.

Пример спирали Архимеда, которая используется в часовом механизме. Изображение представлено Greubel Forsey. Доступно по лицензии CC BY-SA 3.0 из Wikimedia Commons.

В данной статье мы разберём только один вид спирали, а именно, спираль Архимеда, которая изображена в механизме выше. Спираль Архимеда – это особый вид спирали с постоянным расстоянием между витками. Благодаря этому свойству она широко распространена при проектировании катушек и пружин.

Уравнение спирали Архимеда в полярной системе координат записывается, как:

r=a+btheta

где a и b — параметры, определяющие начальный радиус спирали и расстояние между витками, которое равно 2 pi b. Обратите внимание, что спираль Архимеда также иногда называют арифметической спиралью. Это имя связывают с арифметической зависимостью расстояния от начала кривой до точек спирали, находящихся на одной радиальной линии.

Задание параметризированной геометрии спирали Архимеда

Теперь, когда вы уже знаете, что такое спираль Архимеда, давайте приступим к параметризации и созданию геометрии в COMSOL Multiphysics.

Спираль Архимеда может быть задана как в полярных, так и в декартовых координатах.

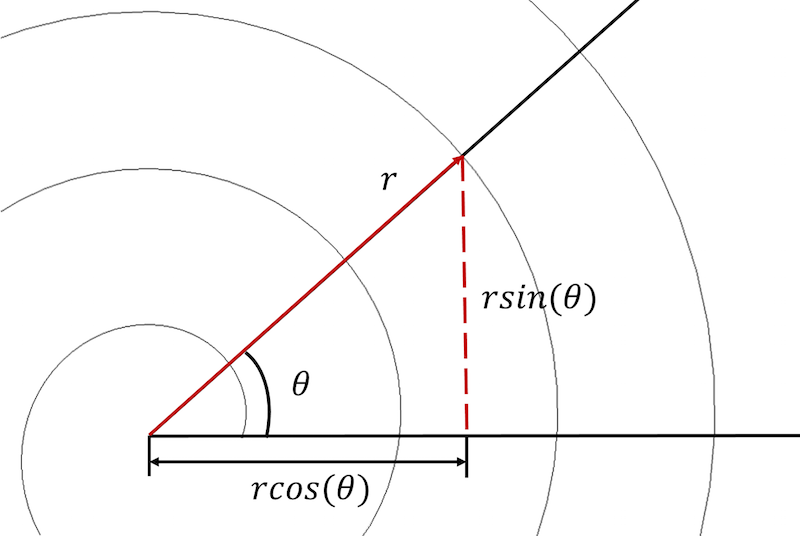
Для начала необходимо преобразовать уравнение спирали из полярной системы координат в декартову и выразить каждое уравнение в параметрической форме:

begin{align*} x_{component}=rcos(theta) \ y_{component}=rsin(theta) end{align*}

После преобразования уравнения спирали в параметрической форме в декартовой системе координат примут вид:

begin{align*} x_{component}=(a+btheta)cos(theta) \ y_{component}=(a+btheta)sin(theta) end{align*}

В COMSOL Multiphysics необходимо определить набор параметров, с помощью которых будем задавать геометрию спирали. В нашем случае — это начальный и конечный радиусы спирали a_{initial} и a_{final}, соответственно, и количество витков n. Показатель роста спирали b находится, как:

b=frac{a_{final}-a_{initial}}{2 pi n}

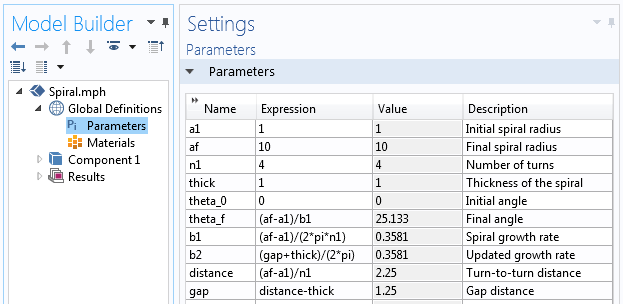
Также необходимо определить начальный и конечный углы спирали — theta_0 и theta_f, соответственно. Давайте с них и начнём — theta_0=0 и theta_f=2 pi n. Исходя из заданной информации, определяем параметры для построения геометрии спирали.

Параметры, которые используются для построения геометрии спирали.

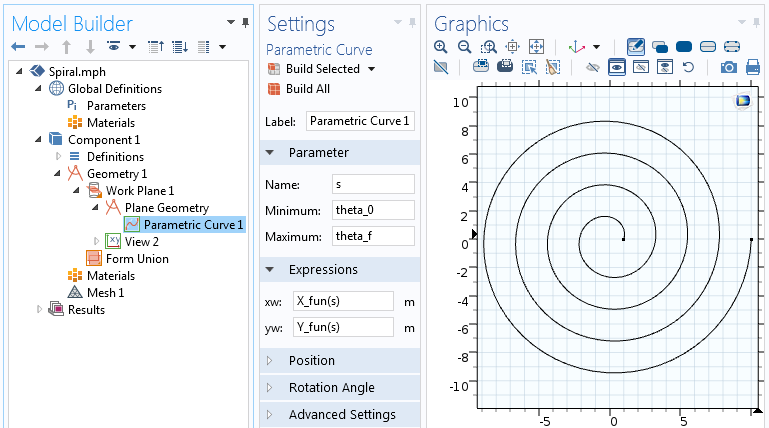
Начнём наше построение, выбрав трёхмерную задачу (3D Component) и создадим Work Plane (Рабочую плоскость) в разделе Geometry (Геометрия). В геометрии для Work Plane добавляем Parametric Curve (Параметрическую кривую) и записываем параметрические уравнения, описанные выше, чтобы задать двухмерную геометрию спирали Архимеда. Данные уравнения можно сразу вписать в соответствующие поля во вкладке Expression либо сначала можно задать каждое уравнение отдельной Аналитической функцией (Analytic function):

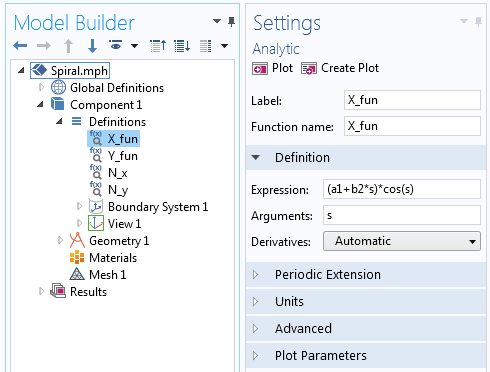
begin{align*} X_{fun}=(a+bs)cos(s) \ Y_{fun}=(a+bs)sin(s) \ end{align*}

Выражение для X-компоненты уравнения спирали Архимеда, заданное аналитической функцией.

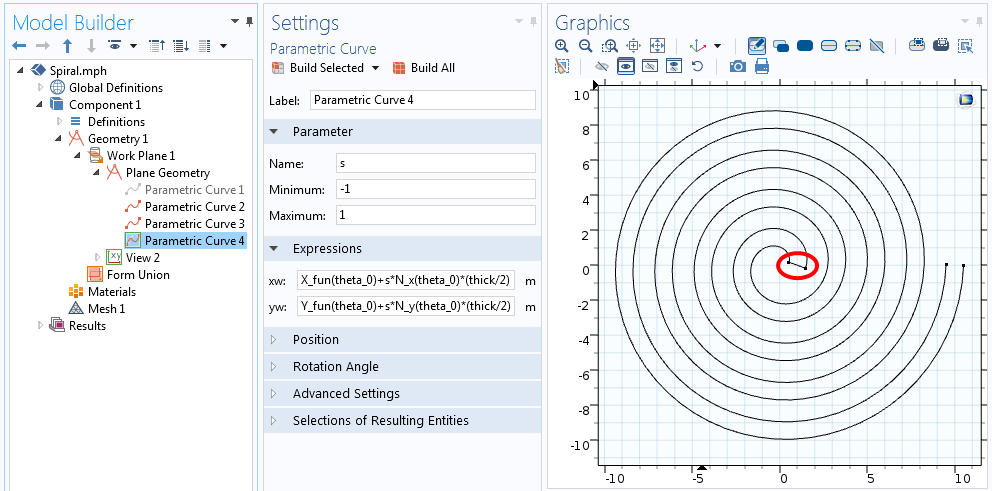
Аналитическая функция затем может использоваться в качестве выражения в узле Parametric Curve. Во вкладке Parameter задаём параметр s от начального угла, theta_0, до его конечного значения, theta_f=2 pi n.

Настройки для Parametric Curve (Параметрической кривой).

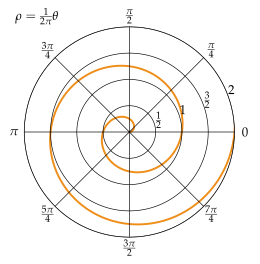
Как только вы зададите все параметры и нажмёте на кнопку «Build Selected», будет построена кривая, изображённая на скриншоте выше. Теперь давайте зададим толщину спирали, чтобы получить твёрдотельную (solid) двухмерную фигуру.

До этого момента параметрами нашей кривой были начальный (a_{initial}) и конечный (a_{final}) радиусы и количество витков n. Теперь мы хотим добавить ещё один – толщину спирали.

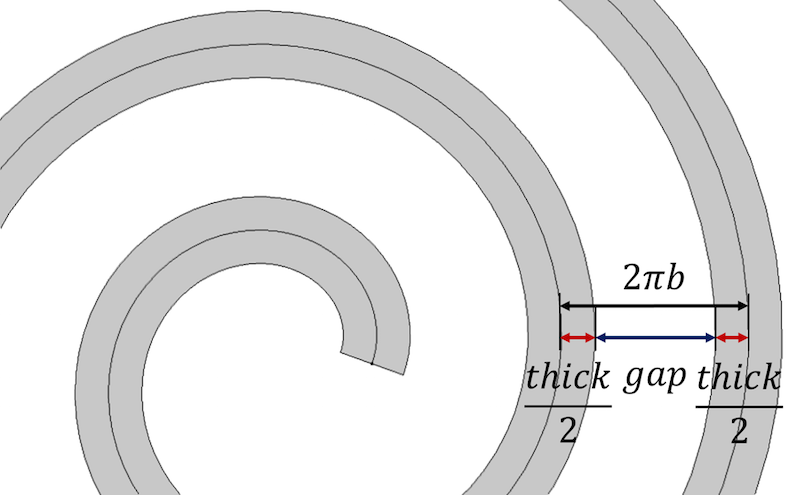
Ещё раз напомним главное свойство спирали — расстояние между витками постоянно и равно 2 pi b. Что эквивалентно frac{a_{final}-a_{initial}}{n}. Чтобы добавить толщину в наши уравнения, представляем расстояние между витками суммой толщины спирали и зазора thick+gap.

Расстояние между витками определяется толщиной спирали и величиной зазора.

Чтобы ввести параметр толщины и сохранить постоянное расстояние между витками, последнее перепишем, как:

begin{align*} distance=frac{a_{initial}-a_{final}}{n} \ gap=distance-thick end{align*}

После этого выражаем показатель роста спирали через толщину:

begin{align*} distance=2pi b \ b=frac{gap+thick}{2pi} end{align*}

Также нужно выразить конечный угол спирали через начальный угол и конечный радиус:

begin{align*} theta_{final}=2 pi n \ a_{final}=text{total distance}+a_{initial} \ a_{final}=2 pi bn+a_{initial} \ n=frac{a_{final}-a_{initial}}{2 pi b} \ theta_{final}=frac{2 pi (a_{final}-a_{initial})}{2 pi b} \ theta_{final}=frac{a_{final}-a_{initial}}{b} end{align*}

Хотите задать отличный от нуля начальный угол спирали? Если так, то его надо будет добавить в выражение для определения конечного угла: theta_f=frac{a_{final}-a_{initial}}{b}+theta_0.

Дублирование кривой спирали дважды со смещением на -frac{thick}{2} и +frac{thick}{2} по отношению к начальной кривой позволяет построить спираль заданной толщины. Чтобы правильно расположить внутреннюю и внешнюю спирали, необходимо убедиться, что начала данных кривых перпендикулярны линии, на которой расположены их начальные точки. Это можно сделать, домножив расстояние смещения pmfrac{thick}{2} на единичный вектор, расположенный по нормали к начальной кривой спирали. Уравнения векторов нормали в параметрическом виде:

n_x=-frac{dy}{ds} quad text{and} quad n_y=frac{dx}{ds}

где s — это параметр, используемый в узле Parametric Curve. Чтобы получить нормированные единичные вектора, необходимо эти выражения разделить на длину нормали:

sqrt{(dx/ds)^2+(dy/ds)^2 }

Обновленные параметрические уравнения спирали Архимеда со смещением:

begin{align*} x_{component}=(a+bs)cos(s)-frac{dy/ds}{sqrt{(dx/ds)^2+(dy/ds)^2}}frac{thick}{2} \ y_{component}=(a+bs)sin(s)+frac{dx/ds}{sqrt{(dx/ds)^2+(dy/ds)^2}}frac{thick}{2} end{align*}

Записывать такие длинные выражения довольно неудобно, поэтому введём следующие обозначения:

begin{align*} N_x=-frac{dy/ds}{sqrt{(dx/ds)^2+(dy/ds)^2}} \ N_y=frac{dx/ds}{sqrt{(dx/ds)^2+(dy/ds)^2 }} end{align*}

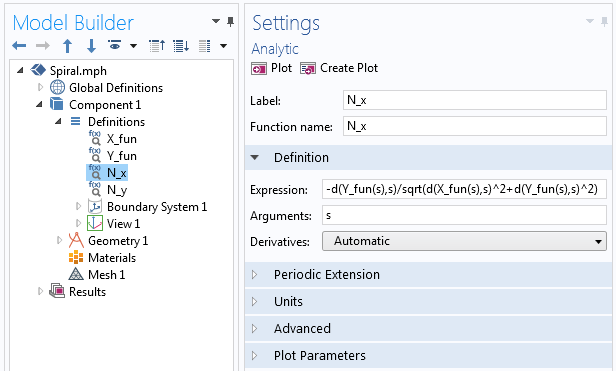
где N_x и N_y определяются аналитическими функциями в COMSOL Multiphysics, аналогично X_{fun} и Y_{fun} в первом примере. Внутри функции используется оператор производной, d(f(x),x), как показано на скриншоте ниже.

Примеры оператора производной, который используется в аналитической функции

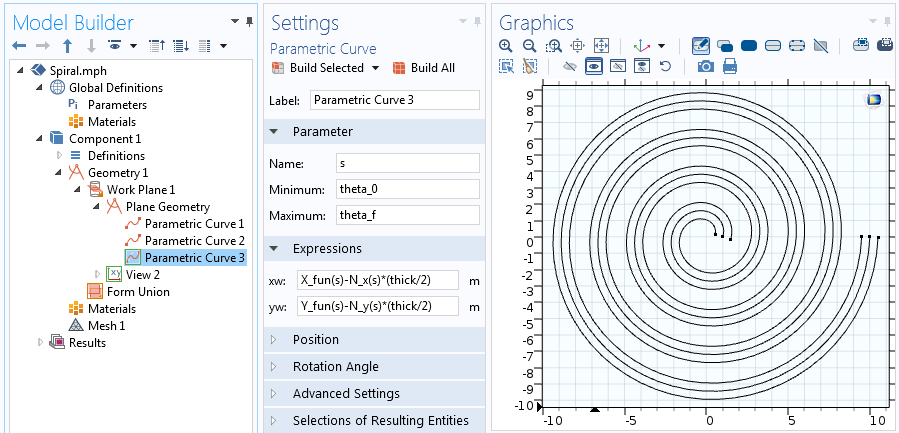
Функции X_{fun}, Y_{fun}, N_x, и N_y могут быть использованы в выражениях для задания параметрической кривой, как с одной стороны:

begin{align*} x_{lower}=X_{fun}(s)+N_x(s)frac{thick}{2} \ y_{lower}=Y_{fun}(s)+N_y(s)frac{thick}{2} end{align*}

Так и с другой:

begin{align*} x_{upper}=X_{fun}(s)-N_x(s)frac{thick}{2} \ y_{upper}=Y_{fun}(s)-N_y(s)frac{thick}{2} end{align*}

Выражения для второй смещённой параметрической кривой.

Чтобы соединить концы, добавим ещё две параметрические кривые, используя незначительные изменения уравнений выше. Для кривой, которая будет соединять спираль в центре, необходимо задать X_{fun}, Y_{fun}, N_x, и N_y для начального значения угла, theta. Для кривой, которая будет соединять концы, необходимо задать конечное значение theta. Исходя из этого, уравнения кривой в центре:

begin{align*} X_{fun}(theta_0)+scdot N_x(theta_0)cdotfrac{thick}{2} \ Y_{fun}(theta_0)+scdot N_y(theta_0)cdotfrac{thick}{2} end{align*}

Уравнения кривой на конце:

begin{align*} X_{fun}(theta_f)+scdot N_x(theta_f)cdotfrac{thick}{2} \ Y_{fun}(theta_f)+scdot N_y(theta_f)cdotfrac{thick}{2} end{align*}

В этих уравнениях параметр s изменяется от -1 до 1, как показано на скриншоте ниже.

Уравнения кривой, соединяющей спираль в центре.

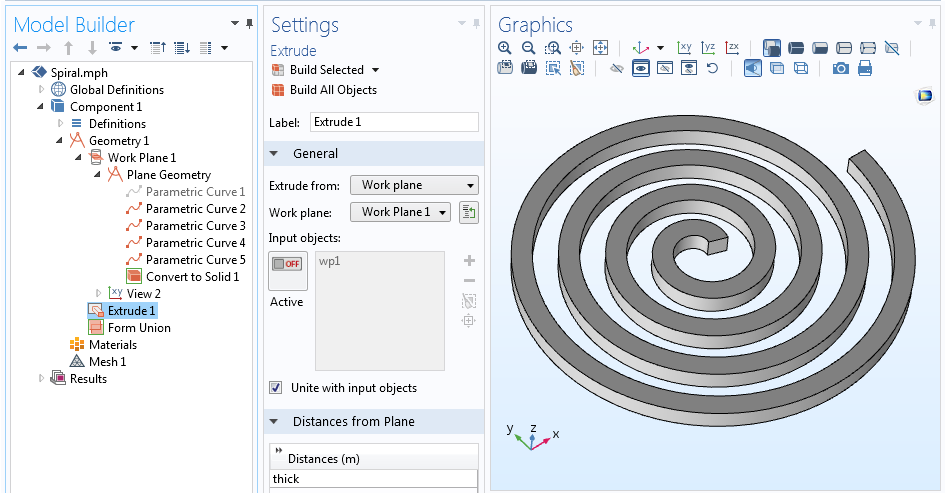
В итоге, мы имеем пять кривых, которые определяют осевую линию спирали и её четыре стороны. Осевую линию можно отключить (функция disable) или даже удалить, так как она не является необходимой. Добавив узел Convert to Solid, создаём единый геометрический объект. Последним шагом является вытягивание данного профиля с помощью операции Extrude и создание трёхмерного объекта.

Полная геометрическая последовательность и вытянутая (экструдированная) трёхмерная геометрия спирали.

Краткие выводы по моделированию спирали Архимеда в COMSOL Multiphysics

В данной заметке мы разобрали основные шаги по созданию параметрической спирали Архимеда. С помощью данной модели вы можете сами экспериментировать с различными значениями параметров, а также попробовать решить с использованием данной параметризации оптимизационную задачу. Надеемся, что данная статья оказалась полезной и вы будете применять данную технику в своих последующих моделях.

Дополнительные ресурсы по проектированию и расчёту спиралей

Для улучшения навыков моделирования спиралей, ознакомьтесь со следующими учебными моделями:
- Спирально-щелевая антенна
Познакомьтесь с опытом одного из наших пользователей: Анализ спиральных резонаторных фильтров

Источник

Архимедова спираль

Архимедова спираль — это кривая описываемая точкой, совершающей одновременно два равномерных движения, одно из которых,
совершается вдоль радиус-вектора ρ, вращающегося вокруг полюса О, а другое — по окружности.
Уравнение спирали имеет вид
ρ=aφ
где:
R — радиус вектор;
a — коэффициент пропорциональности;
φ — угол поворота радиус вектора (полярный угол).

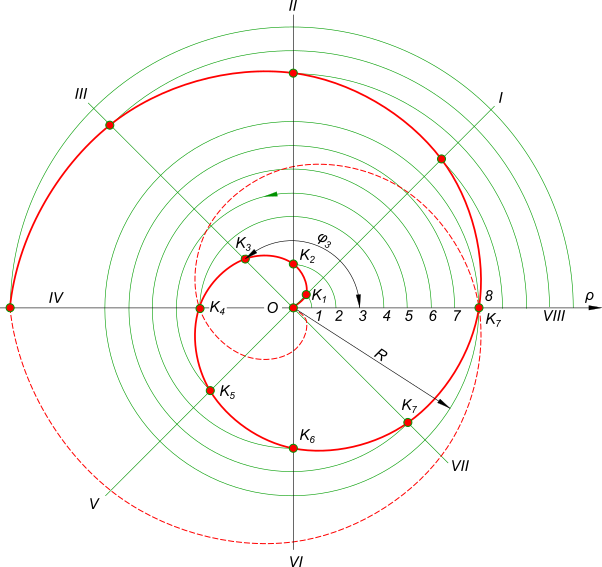
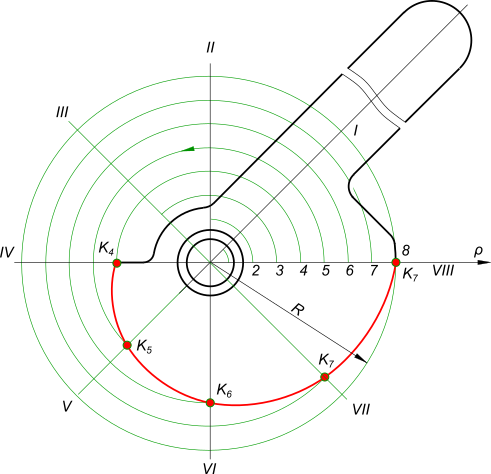
Архимедова спираль может быть построена:
по уравнению ρ=aφ для чего необходимо:
— определить коэффициент пропорциональности;
a = ρ/φ = Rφ/(2π), где R — расстояние между двумя последовательными витками (шаг спирали);
— задаться для каждой искомой точки соответственным значением угла φ;
— решить уравнение ρ=aφ для принятого значения φ.
Архимедова спираль имеет две ветви, одна из которых раскручивается против хода часовой стрелки и соответствует положительному значению φ, другая — по ходу часовой стрелки и соответствует отрицательному значению φ.
графическим способом если заданы шаг спирали R:
— из центра О описываем радиусом R окружность;

— делим отрезок О-VIII, равный R и окружность на одинаковое равное число частей, например на 8. Получим на отрезке О-VIII точки 1; 2; 3 и т. д.,
а на окружности — I, II, III и т. д.;

— из центра О прводим через точки деления окружности пучок лучей ОI, ОII, ОIII и т. д.;
— из центра О описываем дуги окружностей О1, О2, О3 и т. д. до пересечения с соответствующими лучами ОI, ОII, ОIII и т. д.;
— полученные точки K₁; K₂; K₃ и т. д. соединяем плавной кривой.

Архимедова спираль

На представленном рисунке построен один виток. Если потребуется несколько удлинить виток или увеличить число витков, то для их построения
необходимо использовать точки K₁; K₂; K₃ и т. д. основного витка, отложив от каждой из этих точек на лучах ОI, ОII, ОIII и т. д. отрезок, равный
шагу спирали R.

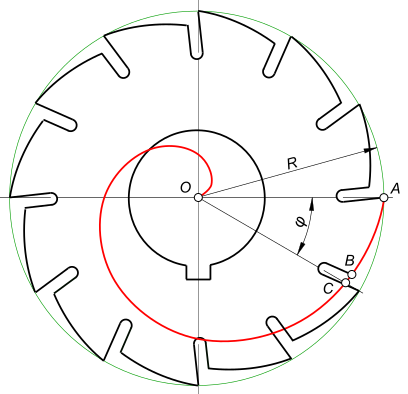
Архимедова спираль широко применяется в технике:
— при конструировании фрез,

Архимедова спираль

по ней выполняют затылование зубьев;
— при конструировании самоцентрирующихся патронов, кулачковых механизмов,

Архимедова спираль

зажимных эксцентриковых приспособлений.

Источник

Derivation of general equation of spiral[edit]

Arc length and curvature [edit]

Characteristics[edit]

General Archimedean spiral[edit]

Applications[edit]

See also[edit]

References[edit]

External links[edit]

Спираль Архимеда

Спираль Архимеда

Как построить спираль Архимеда

Видео – как нарисовать спираль Архимеда

Что такое спираль Архимеда?

Задание параметризированной геометрии спирали Архимеда

Краткие выводы по моделированию спирали Архимеда в COMSOL Multiphysics

Дополнительные ресурсы по проектированию и расчёту спиралей

Архимедова спираль

Не пропустите также: