Как найти радиус шара вписанного в пирамиду - AvtoShod.ru

В данной публикации представлены формулы, с помощью которых можно найти радиус шара (сферы), вписанного в правильную пирамиду: треугольную, четырехугольную, шестиугольную и тетраэдр.

Формулы расчета радиуса шара (сферы)
- Правильная треугольная пирамида
- Правильная четырехугольная пирамида
- Правильная шестиугольная пирамида

Формулы расчета радиуса шара (сферы)

Приведенная ниже информация применима только к правильным пирамидам. Формула для нахождения радиуса зависит от вида фигуры, рассмотрим самые распространенные варианты.

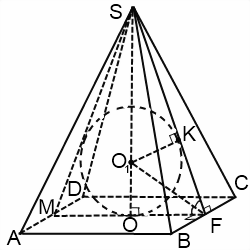
Правильная треугольная пирамида

На рисунке:

a – ребро основания пирамиды, т.е. это равные отрезки AB, AC и BC;
DE – высота пирамиды (h).

Если известны значения этих величин, то найти радиус (r) вписанного шара/сферы можно по формуле:

Частный случай правильной треугольной пирамиды – это правильный тетраэдр. Для него формула нахождения радиуса выглядит следующим образом:

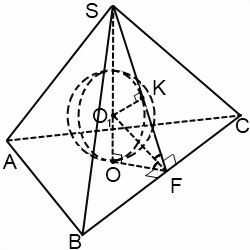
Правильная четырехугольная пирамида

На рисунке:

a – ребро основания пирамиды, т.е. AB, BC, CD и AD;
EF – высота пирамиды (h).

Радиус (r) вписанного шара/сферы рассчитывается так:

Правильная шестиугольная пирамида

На рисунке:

a – ребро основания пирамиды, т.е. AB, BC, CD, DE, EF, AF;
GL – высота пирамиды (h).

Радиус (r) вписанного шара/сферы вычисляется по формуле:

Источник

Чтобы легко справиться с решением задач на шар, вписанный в пирамиду, полезно разобрать небольшой теоретический материал.

Шар вписан в пирамиду (или сфера вписана в пирамиду) — значит, шар (сфера) касаются каждой грани пирамиды. Плоскости, содержащие грани пирамиды, являются касательными плоскостями шара. Отрезки, соединяющие центр шара с точками касания, перпендикуляры к касательным плоскостям. Их длины равны радиусу шара. Центр вписанного в пирамиду шара — точка пересечения бисекторных плоскостей двугранных углов при основании (то есть плоскостей, делящих эти углы пополам).

Чаще всего в задачах речь идет о шаре, вписанном в правильную пирамиду. Шар можно вписать в любую правильную пирамиду. Центр шара в этом случае лежит на высоте пирамиды. При решении задачи удобно провести сечение пирамиды и шара плоскостью, проходящей через апофему и высоту пирамиды.

Если пирамида четырехугольная или шестиугольная, сечение представляет собой равнобедренный треугольник, боковые стороны которого — апофемы, а основание — диаметр вписанной в основание окружности.

Если пирамида треугольная или пятиугольная, достаточно рассмотреть лишь часть этого сечения — прямоугольный треугольник, катеты которого — высота пирамиды и радиус вписанной в основание пирамиды окружности, а гипотенуза — апофема.

В любом случае, в итоге приходим к рассмотрению соответствующего прямоугольного треугольника и других связанных с ним треугольников.

Итак, в прямоугольном треугольнике SOF катет SO=H — высота пирамиды, катет OF=r — радиус вписанной в основание пирамиды окружности, гипотенуза SF=l — апофема пирамиды. O1- центр шара и, соответственно, окружности, вписанной в треугольник, полученный в сечении (мы рассматриваем его часть). Угол SFO — линейный угол двугранного угла между плоскостью основания и плоскостью боковой грани SBC. Точки K и O — точки касания, следовательно, O1K перпендикулярен SF. OO1=O1K=R — радиусу шара.

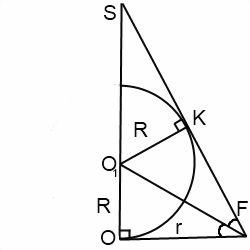
Прямоугольные треугольники OO1F и KO1F равны (по катетам и гипотенузе). Отсюда KF=OF=r.

Прямоугольные треугольники SKO1 и SOF подобны (по острому углу S), откуда следует, что

$[frac{{OF}}{{K{O_1}}} = frac{{SO}}{{SK}}, Rightarrow frac{r}{R} = frac{H}{{l - r}}.]$

В треугольнике SOF применим свойство биссектрисы треугольника:

$[frac{{SF}}{{S{O_1}}} = frac{{OF}}{{O{O_1}}}, Rightarrow frac{l}{{H - R}} = frac{r}{R}.]$

Из прямоугольного треугольника OO1F

$[tgangle OF{O_1} = frac{{O{O_1}}}{{OF}} = frac{R}{r}.]$

При решении задач на шар, вписанный в правильную пирамиду, будет полезным еще одно рассуждение.

$[frac{l}{{H - R}} = frac{r}{R}, Rightarrow Rl = (H - R)r, Rightarrow ]$

$[R = frac{{rH}}{{l + r}}.]$

Теперь найдем отношение объема пирамиды к площади ее поверхности:

$[frac{V}{{{S_{n.n/}}}} = frac{{frac{1}{3}{S_{ocn}} cdot H}}{{{S_{ocn}} + {S_{bok}}}} = frac{1}{3} cdot frac{{prH}}{{pr + pl}} = ]$

$[ = frac{1}{3} cdot frac{{rH}}{{r + l}} = frac{1}{3}R.]$

Таким образом, радиус вписанного шара выражается через объем пирамиды и ее полную поверхность:

$[R = frac{{3V}}{{{S_{n.n.}}}}.]$

Все эти рассуждения верны не только для правильной пирамиды, но и для пирамиды, основание высоты которой совпадает с центром вписанной в основание окружности (то есть для пирамиды, у которой все двугранные углы при основании равны).

Источник

Задача 4.

Найти радиус шара, вписанного в правильную треугольную пирамиду, сторона основания которой равна а и двугранный угол пирамиды при ребре основания равен альфа.