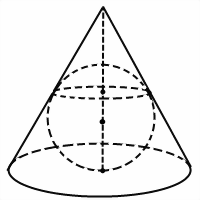
В данной публикации мы рассмотрим, как найти радиус вписанного в конус шара (сферы), а также площадь его поверхности и объем.
- Нахождение радиуса шара/сферы
- Формулы площади и объема шара/сферы
Нахождение радиуса шара/сферы
В любой конус можно вписать шар (сферу). Другими словами, вокруг любого шара можно описать конус.
Чтобы найти радиус шара (сферы), вписанного в конус, чертим осевое сечение конуса. Таким образом, мы получаем равнобедренный треугольник (в нашем случае – ABC), в который вписана окружность радиусом r.
Радиус основания конуса (R) равняется половине основания данного треугольника (AC), а образующие (l) являются его боковыми сторонами (AB и BC).
Радиус окружности, вписанной в равнобедренный треугольник ABC, в том числе, является радиусом шара, вписанного в конус. Он находится по формуле:
Формулы площади и объема шара/сферы
Зная радиус (r) можно найти площадь поверхности (S) сферы и объем (V) шара, ограниченного этой сферой:
Примечание: π округленно равняется 3,14.
Нахождение радиуса/площади/объема вписанного в конус шара (сферы)
В данной публикации мы рассмотрим, как найти радиус вписанного в конус шара (сферы), а также площадь его поверхности и объем.
Нахождение радиуса шара/сферы
В любой конус можно вписать шар (сферу). Другими словами, вокруг любого шара можно описать конус.
Чтобы найти радиус шара (сферы), вписанного в конус, чертим осевое сечение конуса. Таким образом, мы получаем равнобедренный треугольник (в нашем случае – ABC), в который вписана окружность радиусом r.
Радиус основания конуса (R) равняется половине основания данного треугольника (AC), а образующие ( l ) являются его боковыми сторонами (AB и BC).
Радиус окружности, вписанной в равнобедренный треугольник ABC, в том числе, является радиусом шара, вписанного в конус. Он находится по формуле:
Формулы площади и объема шара/сферы
Зная радиус (r) можно найти площадь поверхности (S) сферы и объем (V) шара, ограниченного этой сферой:
Примечание: π округленно равняется 3,14.
Узнать ещё
Знание — сила. Познавательная информация
Шар, вписанный в конус
Рассмотрим некоторые соотношения, которые полезны при решении задач на шар, вписанный в конус.
В любой конус можно вписать шар. Вписанный в конус шар (или сфера, вписанная в конус) касается основания конуса в его центре, а боковой поверхности — по окружности. Центр шара (сферы) лежит на оси конуса.
При решении задач на шар, вписанный в конус, удобнее всего рассмотреть сечение комбинации тел плоскостью, проходящей через ось конуса и центр шара.
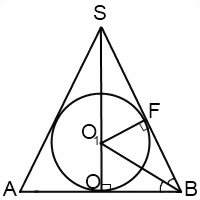
Это сечение представляет собой равнобедренный треугольник, боковые стороны которого — образующие конуса, а основание — диаметр конуса. Вписанный в этот треугольник круг — большой круг шара (то есть круг, радиус которого равен радиусу шара).
Для данного рисунка образующие SA=SB=l, высота конуса SO=H, радиус вписанного шара OO1=O1F=R. Так как центр вписанного круга — точка пересечения биссектрис треугольника, то ∠OBO1=∠FBO1, OB=r — радиус конуса.
Рассмотрим прямоугольный треугольник SOB. По свойству биссектрисы треугольника:
По теореме Пифагора
Рассмотрим прямоугольный треугольник OO1B.
Если ∠OBS=α, то ∠OBO1=α/2. Отсюда
Если сначала выразить радиус конуса через его высоту из прямоугольного треугольника SOB
то из треугольника OO1B выражаем радиус шара через высоту конуса:
Радиус и образующая конуса
Свойства
Поскольку радиус конуса характеризует размер его основания, то зная его, можно найти диаметр, длину окружности и площадь круга, лежащего в основании. Диаметр представляет собой удвоенный радиус, длина окружности – удвоенный радиус, умноженный на число π, а площадь круга – квадрат радиуса, умноженный на число π. d=2r P=2πr S_(осн.)=πr^2
Зная радиус и образующую конуса, можно уже найти его высоту, угол между образующей и основанием, угол раствора конуса. Высота конуса через радиус и образующую ищется по теореме Пифагора в прямоугольном треугольнике, оттуда же можно вычислить и угол β через тригонометрические отношения сторон. Угол α можно найти из равнобедренного треугольника, образованного двумя образующими и диаметром, отняв из 180 градусов два угла β. (рис.40.1, 40.2) h=√(l^2-r^2 ) cosβ=r/l α=180°-2β
Площадь боковой поверхности конуса равна произведению полупериметра основания на образующую или произведению числа π на радиус и образующую. Чтобы найти площадь полной поверхности, зная радиус и образующую конуса, необходимо прибавить к площади боковой поверхности произведение числа π на квадрат радиуса, что является площадью основания конуса. S_(б.п.)=πrl S_(п.п.)=S_(б.п.)+S_(осн.)=πrl+πr^2=πr(l+r)
Объем конуса, также как и объем пирамиды рассчитывается как одна треть основания, умноженная на высоту. V=1/3 S_(осн.) h=(πr^2 h)/3
Радиус сферы, вписанной в конус, вычисляется как произведение высоты на радиус конуса, деленное на сумму радиуса и образующей. Радиус сферы, описанной вокруг конуса, представляет собой отношение квадрата образующей к удвоенной высоте. (рис.40.3, 40.4) r_1=hr/(l+r)=(r√(l^2-r^2 ))/(l+r) R=l^2/2h
Рассмотрим некоторые соотношения, которые полезны при решении задач на шар, вписанный в конус.
В любой конус можно вписать шар. Вписанный в конус шар (или сфера, вписанная в конус) касается основания конуса в его центре, а боковой поверхности — по окружности. Центр шара (сферы) лежит на оси конуса.
При решении задач на шар, вписанный в конус, удобнее всего рассмотреть сечение комбинации тел плоскостью, проходящей через ось конуса и центр шара.
Для данного рисунка образующие SA=SB=l, высота конуса SO=H, радиус вписанного шара OO1=O1F=R. Так как центр вписанного круга — точка пересечения биссектрис треугольника, то ∠OBO1=∠FBO1, OB=r — радиус конуса.
Рассмотрим прямоугольный треугольник SOB. По свойству биссектрисы треугольника:
По теореме Пифагора
Отсюда
Рассмотрим прямоугольный треугольник OO1B.
Если ∠OBS=α, то ∠OBO1=α/2. Отсюда
Если сначала выразить радиус конуса через его высоту из прямоугольного треугольника SOB
то из треугольника OO1B выражаем радиус шара через высоту конуса:
поделиться знаниями или
запомнить страничку
- Все категории
-
экономические
43,662 -
гуманитарные
33,654 -
юридические
17,917 -
школьный раздел
611,985 -
разное
16,906
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Шар является описанным около куба, если все вершины куба находятся на поверхности шара.

Центр шара (O) — точка пересечения диагоналей куба.
Около любого куба можно описать шар.
Общие точки шара и куба — восемь вершин куба.
Чертится диагональное сечение.
и
CA1
— диагонали куба.
Радиус шара равен половине диагонали куба.
Шар является вписанным в куб, если он касается всех его граней.

Центр шара (O) находится в точке пересечения диагоналей куба.
В любой куб можно вписать шар.
Общие точки шара и куба — центры шести граней куба (точки касания шара и куба).
Чертится сечение плоскостью, которая параллельна грани куба и проходит через центр шара.
Радиус шара — половина стороны куба.
Шар является описанным около цилиндра, если окружности оснований цилиндра лежат на поверхности шара.

Центр шара (O) находится в середине высоты цилиндра.
Общие элементы — две окружности.
Около любого цилиндра можно описать шар.
Чертится осевое сечение.
Радиус шара — половина диагонали осевого сечения цилиндра.
Шар является вписанным в цилиндр, если касается оснований цилиндра и всех его образующих.
Центр шара (O) — середина высоты цилиндра.
Осевое сечение — квадрат с вписанной в него окружностью.
Радиус шара равен радиусу цилиндра и половине высоты цилиндра.