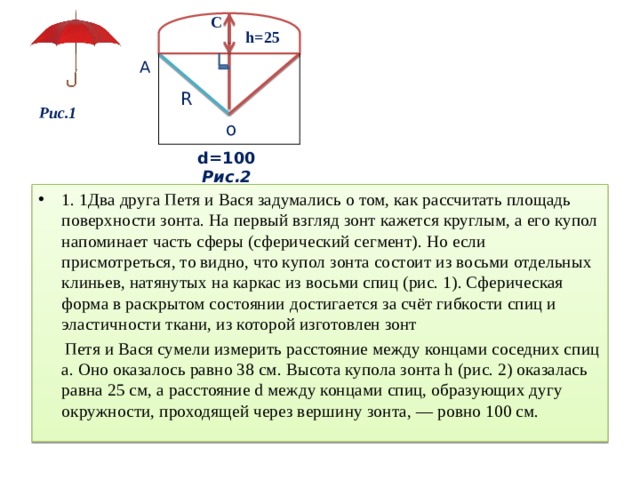
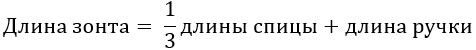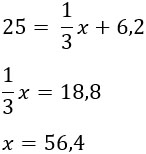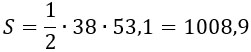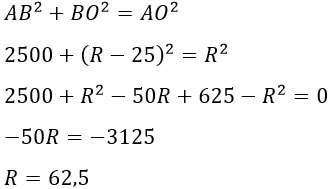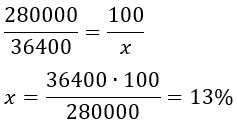Два друга Петя и Вася задумались о том, как рассчитать площадь поверхности зонта.
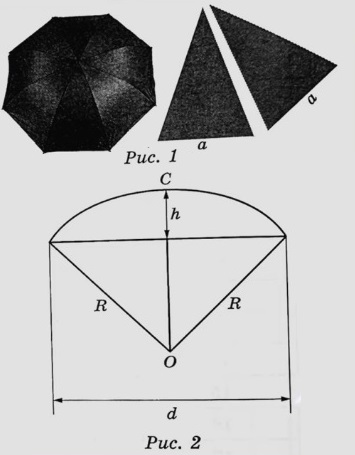
На первый взгляд зонт кажется круглым, а его купол напоминает часть сферы (сферический сегмент). Но если присмотреться, то видно, что купол зонта состоит из восьми отдельных клиньев, натянутых на каркас из восьми спиц (рис. 1). Сферическая форма в раскрытом состоянии достигается за счёт гибкости спиц и эластичности ткани, из которой изготовлен зонт.
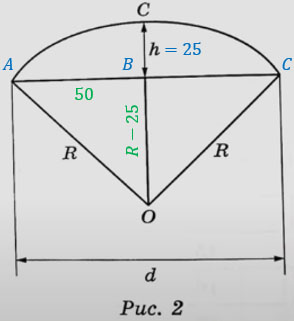
Петя и Вася сумели измерить расстояние между концами соседних спиц а. Оно оказалось равно 38 см. Высота купола зонта h (рис. 2) оказалась равна 25 см, а расстояние d между концами спиц, образующих дугу окружности, проходящей через вершину зонта, – ровно 100 см.
Источник: ОГЭ Ященко 2023 (36 вар)
Задание 1
Длина зонта в сложенном виде равна 25 см и складывается из длины ручки (рис. 3) и трети длины спицы (зонт в три сложения). Найдите длину спицы, если длина ручки зонта равна 6,2 см.
Решение
Найдём треть длины спицы, отняв от длины всего зонта длину ручки:
25 см – 6,2 см = 18,8 см
Если это треть, то вся спица в 3 раза больше:
18,8·3 = 56,4 см
Ответ: 56,4.
Задание 2
Поскольку зонт сшит из треугольников, рассуждал Петя, площадь его поверхности можно найти как сумму площадей треугольников. Вычислите площадь поверхности зонта методом Пети, если высота каждого равнобедренного треугольника, проведённая к основанию, равна 53,1 см. Ответ дайте в квадратных сантиметрах с округлением до десятков.
Решение
По первому условию зонт состоит из 8 треугольников с основанием а = 38 см и высотой h = 53,1 см.
Площадь одного такого треугольника:
S_{Delta}=frac{1}{2}ah=frac{1}{2}cdot 38cdot 53,1=19cdot 53,1=1008,9
Найдём площадь поверхности зонта, методом Пети, округлив до ДЕСЯТКОВ:
Sповерхности = 8·SΔ = 8·1008,9 = 8071,2 ≈ 8070 см2
Ответ: 8070.
Задание 3
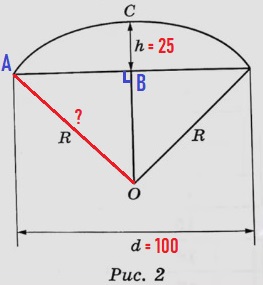
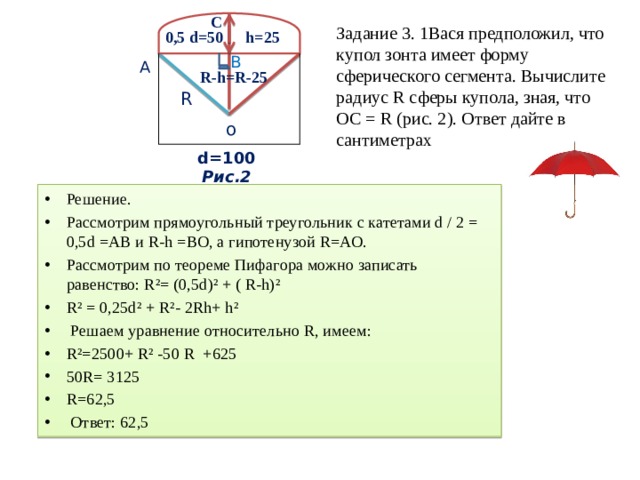
Вася предположил, что купол зонта имеет форму сферического сегмента. Вычислите радиус R сферы купола, зная, что ОС = R (рис. 2). Ответ дайте в сантиметрах.
Решение
Нам необходимо найти гипотенузу R в прямоугольном треугольнике АВО. АВ равно половине d:
AB = d/2 = 100/2 = 50
Т.к. по условию ОС = R, то:
ОВ = ОС – h = R – 25
По теореме Пифагора найдём ОА = R:
ОА2 = АВ2 + ОВ2
R2 = 502 + (R – 25)2
R2 = 2500 + R2 – 50R + 625
R2 – R2 + 50R = 3125
50R = 3125
R = 3125/50 = 62,5
Ответ: 62,5.
Задание 4
Вася нашёл площадь купола зонта как площадь поверхности сферического сегмента по формуле S = 2πRh‚ где R – радиус сферы, а h – высота сегмента. Рассчитайте площадь поверхности купола способом Васи. Число π округлите до 3,14. Ответ дайте в квадратных сантиметрах с округлением до целого.
Решение
S = 2πRh
π ≈ 3,14
R = 62,5
h = 25
Найдём площадь и округлим до целого:
S = 2πRh = 2·3,14·62,5·25 = 50·3,14·62,5 = 9812,5 ≈ 9813 см2
Ответ: 9813.
Задание 5
Рулон ткани имеет длину 35 м и ширину 80 см. На фабрике из этого рулона были вырезаны треугольные клинья для 29 зонтов, таких же, как зонт, который был у Пети и Васи. Каждый треугольник с учётом припуска на швы имеет площадь 1050 кв. см. Оставшаяся ткань пошла в обрезки. Сколько процентов ткани рулона пошло в обрезки?
Решение:
Найдём площадь рулона ткани в см2:
S = 35м х 80см = 3500см х 80см = 280000 см2
Помня, что в одном зонте 8 треугольников найдём сколько ушло ткани на 29 зонтов:
S1 = 29·8·1050 = 243600 см2
Найдём сколько см2 ткани рулона ушло в обрезки:
S2 = S – S1 = 280000 – 243600 = 36400 см2
Найдём сколько это процентов от начального рулона:
frac{36400}{280000}cdot 100%=frac{364}{2800}cdot 100%=frac{91}{700}cdot 100%=frac{13}{100}cdot 100%=13%
Ответ: 13.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 4.8 / 5. Количество оценок: 388
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.
Прочитайте внимательно текст и выполните задания 1 — 5.


Решение: Обозначим за Х см длину спицы. Из условия известно, что треть длины спицы и ручка зонта составляют в сумме 25 см.
Составим уравнение: 1/3Х + 6,2 = 25,
1/3Х = 18,8,
Х = 18,8 * 3,
Х = 56,4 (см) — длина спицы зонта.
Ответ: 56,4.
Задание 2 (ОГЭ 2021 зонт)
Поскольку зонт сшит из треугольников, рассуждал Петя, сумму его поверхностей можно найти как сумму площадей треугольников. Вычислите площадь поверхности зонта методом Пети, если высота каждого равнобедренного треугольника, проведенная к основанию, равна 53,1 см. Ответ дайте в квадратных сантиметрах с округлением до десятков.
Решение:
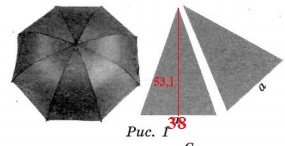
Площадь поверхности зонта состоит из 8 равных равнобедренных треугольников. Проведем высоту в треугольнике на рисунке 1. Найдем площадь одного треугольника.
S = 1/2ah = 1/2 * 38 * 53,1 = 1008,9 (кв. см).
Найдем площадь поверхности зонта.
S = 8 * 1008,9 = 8071,2 ≈ 8070 (см. кв.).
Ответ: 8070.
Задание 3 (ОГЭ 2021 зонт)
Вася предположил, что купол зонта имеет форму сферического сегмента. Вычислите радиус R сферы купола, зная, что OC = R (рис. 2). Ответ дайте в сантиметрах.
Решение:
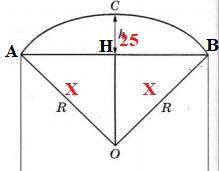
OC = R.
Рассмотрим прямоугольный треугольник AHC. Обозначим OA = x (радиус). Тогда OH = OC — HC = x — 25, AH = 50 см (половина AB из условия).
Применим теорему Пифагора.
OA2 = OH2 + AH2,
x2 = (x — 25)2 + 502,
x2 = x 2 — 50x + 625 + 2500,
50x = 3125,
x = 62,5 (см) — радиус сферы купола зонта.
Ответ: 62,5.
Задание 4 (ОГЭ 2021 зонт)
Вася нашел площадь купола зонта как площадь поверхности сферического сегмента по формуле S = 2ПRh, где R — радиус сферы, а h — высота сегмента. Рассчитайте площадь поверхности купола способом Васи. Число П округлите до 3,14. Ответ дайте в квадратных сантиметрах с округлением до целого.
Решение: S = 2ПRh = 2 * 3,14 * 62,5 * 25 = 9812,5 ≈ 9813 (кв. см).
Ответ: 9813.
Задание 5 (ОГЭ 2021 зонт)
Рулон ткани имеет длину 35 м и ширину 80 см. На фабрике из этого рулона были вырезаны треугольные клинья для 29 зонтов, таких же, как зонт, который был у Пети и Васи. Каждый треугольник с учётом припуска на швы имеет площадь 1050 кв. см. Оставшаяся ткань пошла в обрезки. Сколько процентов ткани рулона пошло в обрезки?
Решение: 35 м = 3500 см.
Найдем площадь рулона ткани. S = 3500 * 80 = 280000 (кв. см).
Рассчитаем сколько ткани ушло на один зонт. 8 * 1050 = 8400 (кв. см).
8400 * 29 = 243600 (кв. см) — ткани нужно на пошив 29 зонтов.
280000 — 243600 = 36400 (кв. см) — обрезки.
Составим пропорцию для нахождения процентов ткани (x%), которая пошла на обрезки.
280000 — 100%
36400 — x%
Найдем неизвестный член пропорции.
х = (36400 * 100) / 280000 = 13%.
Ответ: 13.
Разбираем практико-ориентированные задания 1 — 5 ОГЭ (маркировка автомобильных шин) по математике 2021.
1. Длина зонта в сложенном состоянии равна 25 см и складывается из длины ручки (рис. 3) и трети длины спицы (зонт в три сложения). Найдите длину спицы, если длина ручки зонта равна 6,2 см.
Представим условие задачи в виде формулы:
Обозначим длину спицы за х, подставим все величины в формулу и решим получившееся линейное уравнение:
Ответ: 56,4.
2. Поскольку зонт сшит из треугольников, рассуждал Петя, площадь его поверхности можно найти как сумму площадей треугольников. Вычислите площадь поверхности зонта методом Пети, если высота каждого равнобедренного треугольника, проведенная к основанию, равна 53,1 см. Ответ дайте в квадратных сантиметрах с округлением до десятков.
Площадь треугольника равна половине произведения основания и высоты, проведенной к этому основанию.
Высота дана и равна 53,1. Основание, а оно же — расстояние между концами соседних спиц, тоже дано и равно 38.
Найдем площадь одного треугольника:
Не забываем, что зонт состоит из восьми таких треугольников, их общая площадь будет равна
1008,9 · 8 = 8071,2.
Осталось округлить это число до десятков. За десятки отвечает цифра 7; после нее стоит цифра 1, значит цифра 7 остается без изменений, а все числа после нее обращаются в 0. Таким образом, 8071,2 ≈ 8070.
Ответ: 8070.
3. Вася предположил, что купол зонта имеет форму сферического сегмента. Вычислите радиус R сферы купола, зная, что ОС=R (рис. 2). Ответ дайте в сантиметрах.
Из условия задачи нам известны h = 25 и d = AC = 100.
Зонт — это симметричная вещица, поэтому АВ = ВС = 50.
Если ОС = R и h = 25, то ОВ = R — 25.
Рассмотрим треугольник АВО. Очевидно, что он прямоугольный. Через теорему Пифагора найдем R:
Ответ: 62,5.
4. Вася нашел площадь купола зонта как площадь поверхности сферического сегмента по формуле S=2πRh, где R – радиус сферы, а h – высота сегмента. Рассчитайте площадь поверхности купола способом Васи. Число π округлите до 3,14. Ответ дайте в квадратных сантиметрах с округлением до целого.
R = 62,5 — из предыдущей задачи;
h = 25 — высота сегмента и высота купола равны между собой.
S = 2 · 3,14 · 62,5 · 25 = 9812,5 ≈ 9813.
Ответ: 9813.
5. Рулон ткани имеет длину 35 м и ширину 80 см. На фабрике из этого рулона были вырезаны треугольные клинья для 29 зонтов, таких же, как зонт, который был у Пети и Васи. Каждый треугольник с учетом припуска на швы имеет площадь 1050 кв. см. Оставшаяся ткань пошла в обрезки. Сколько процентов ткани рулона пошла в обрезки?
Один зонт состоит из восьми треугольников, тогда 29 зонтов будут состоять из 232 треугольников.
Если на один треугольник требуется 1050 см2 ткани, то на 232 треугольника нужно будет 1050 · 232 = 243 600 см2.
Площадь ткани в рулоне равна 3500 · 80 = 280 000 см2.
Площадь ткани, ушедшей в обрезки, равна 280 000 — 243 600 = 36 400 см2.
Пусть 280 000 см2 — 100%, а 36 400 — х%. Составим и решим пропорцию:
Ответ: 13.
А вы тоже находите проблему из ничего, как Вася и Петя?)
Не можешь найти нужную задачу? Предложи свою! Наша группа в VK.
Два друга Петя и Вася задумались о том, как рассчитать площадь поверхности зонта.
На первый взгляд зонт кажется круглым, а его купол напоминает часть сферы (сферический сегмент). Но если присмотреться, то видно, что купол зонта состоит из восьми отдельных клиньев, натянутых на каркас из восьми спиц (рис. 1). Сферическая форма в раскрытом состоянии достигается за счёт гибкости спиц и эластичности ткани, из которой изготовлен зонт.
Петя и Вася сумели измерить расстояние между концами соседних спиц а. Оно оказалось равно 38 см. Высота купола зонта h (рис. 2) оказалась равна 25 см, а расстояние d между концами спиц, образующих дугу окружности, проходящей через вершину зонта, – ровно 100 см.
Задание 1
Длина зонта в сложенном виде равна 25 см и складывается из длины ручки (рис. 3) и трети длины спицы (зонт в три сложения). Найдите длину спицы, если длина ручки зонта равна 6,2 см.
Решение
Найдём треть длины спицы, отняв от длины всего зонта длину ручки:
25 см – 6,2 см = 18,8 см
Если это треть, то вся спица в 3 раза больше:
18,8·3 = 56,4 см
Ответ: 56,4.
Задание 2
Поскольку зонт сшит из треугольников, рассуждал Петя, площадь его поверхности можно найти как сумму площадей треугольников. Вычислите площадь поверхности зонта методом Пети, если высота каждого равнобедренного треугольника, проведённая к основанию, равна 53,1 см. Ответ дайте в квадратных сантиметрах с округлением до десятков.
Решение
По первому условию зонт состоит из 8 треугольников с основанием а = 38 см и высотой h = 53,1 см.
Площадь одного такого треугольника:
S_{Delta}=frac{1}{2}ah=frac{1}{2}cdot 38cdot 53,1=19cdot 53,1=1008,9
Найдём площадь поверхности зонта, методом Пети, округлив до ДЕСЯТКОВ:
Sповерхности = 8·SΔ = 8·1008,9 = 8071,2 ≈ 8070 см2
Ответ: 8070.
Задание 3
Вася предположил, что купол зонта имеет форму сферического сегмента. Вычислите радиус R сферы купола, зная, что ОС = R (рис. 2). Ответ дайте в сантиметрах.
Решение
Нам необходимо найти гипотенузу R в прямоугольном треугольнике АВО. АВ равно половине d:
AB = d/2 = 100/2 = 50
Т.к. по условию ОС = R, то:
ОВ = ОС – h = R – 25
По теореме Пифагора найдём ОА = R:
ОА2 = АВ2 + ОВ2
R2 = 502 + (R – 25)2
R2 = 2500 + R2 – 50R + 625
R2 – R2 + 50R = 3125
50R = 3125
R = 3125/50 = 62,5
Ответ: 62,5.
Задание 4
Вася нашёл площадь купола зонта как площадь поверхности сферического сегмента по формуле S = 2πRh‚ где R – радиус сферы, а h – высота сегмента. Рассчитайте площадь поверхности купола способом Васи. Число π округлите до 3,14. Ответ дайте в квадратных сантиметрах с округлением до целого.
Решение
S = 2πRh
π ≈ 3,14
R = 62,5
h = 25
Найдём площадь и округлим до целого:
S = 2πRh = 2·3,14·62,5·25 = 50·3,14·62,5 = 9812,5 ≈ 9813 см2
Ответ: 9813.
Задание 5
Рулон ткани имеет длину 35 м и ширину 80 см. На фабрике из этого рулона были вырезаны треугольные клинья для 29 зонтов, таких же, как зонт, который был у Пети и Васи. Каждый треугольник с учётом припуска на швы имеет площадь 1050 кв. см. Оставшаяся ткань пошла в обрезки. Сколько процентов ткани рулона пошло в обрезки?
Решение:
Найдём площадь рулона ткани в см2:
S = 35м х 80см = 3500см х 80см = 280000 см2
Помня, что в одном зонте 8 треугольников найдём сколько ушло ткани на 29 зонтов:
S1 = 29·8·1050 = 243600 см2
Найдём сколько см2 ткани рулона ушло в обрезки:
S2 = S – S1 = 280000 – 243600 = 36400 см2
Найдём сколько это процентов от начального рулона:
frac{36400}{280000}cdot 100%=frac{364}{2800}cdot 100%=frac{91}{700}cdot 100%=frac{13}{100}cdot 100%=13%
Ответ: 13.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 4.7 / 5. Количество оценок: 203
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время
В отзыве оставь контакт для связи, если хочешь, что бы я тебе ответил.
Вася предположил, что купол зонта имеет форму сферического сегмента. Вычислите радиус R сферы купола, зная, что ОС = R . Ответ дайте в сантиметрах.
Решение.
Видео 9кл.Огэ.Вася предположил, что купол зонта имеет форму сферического сегмента. Вычислите радиус R канала Тамара Остроушко
Показать
1. Длина зонта в сложенном состоянии равна 25 см и складывается из длины ручки (рис. 3) и трети длины спицы (зонт в три сложения). Найдите длину спицы, если длина ручки зонта равна 6,2 см.
Представим условие задачи в виде формулы:
Обозначим длину спицы за х, подставим все величины в формулу и решим получившееся линейное уравнение:
Ответ: 56,4.
2. Поскольку зонт сшит из треугольников, рассуждал Петя, площадь его поверхности можно найти как сумму площадей треугольников. Вычислите площадь поверхности зонта методом Пети, если высота каждого равнобедренного треугольника, проведенная к основанию, равна 53,1 см. Ответ дайте в квадратных сантиметрах с округлением до десятков.
Площадь треугольника равна половине произведения основания и высоты, проведенной к этому основанию.
Высота дана и равна 53,1. Основание, а оно же — расстояние между концами соседних спиц, тоже дано и равно 38.
Найдем площадь одного треугольника:
Не забываем, что зонт состоит из восьми таких треугольников, их общая площадь будет равна
1008,9 · 8 = 8071,2.
Осталось округлить это число до десятков. За десятки отвечает цифра 7; после нее стоит цифра 1, значит цифра 7 остается без изменений, а все числа после нее обращаются в 0. Таким образом, 8071,2 ≈ 8070.
Ответ: 8070.
3. Вася предположил, что купол зонта имеет форму сферического сегмента. Вычислите радиус R сферы купола, зная, что ОС=R (рис. 2). Ответ дайте в сантиметрах.
Из условия задачи нам известны h = 25 и d = AC = 100.
Зонт — это симметричная вещица, поэтому АВ = ВС = 50.
Если ОС = R и h = 25, то ОВ = R — 25.
Рассмотрим треугольник АВО. Очевидно, что он прямоугольный. Через теорему Пифагора найдем R:
Ответ: 62,5.
4. Вася нашел площадь купола зонта как площадь поверхности сферического сегмента по формуле S=2πRh, где R – радиус сферы, а h – высота сегмента. Рассчитайте площадь поверхности купола способом Васи. Число π округлите до 3,14. Ответ дайте в квадратных сантиметрах с округлением до целого.
R = 62,5 — из предыдущей задачи;
h = 25 — высота сегмента и высота купола равны между собой.
S = 2 · 3,14 · 62,5 · 25 = 9812,5 ≈ 9813.
Ответ: 9813.
5. Рулон ткани имеет длину 35 м и ширину 80 см. На фабрике из этого рулона были вырезаны треугольные клинья для 29 зонтов, таких же, как зонт, который был у Пети и Васи. Каждый треугольник с учетом припуска на швы имеет площадь 1050 кв. см. Оставшаяся ткань пошла в обрезки. Сколько процентов ткани рулона пошла в обрезки?
Один зонт состоит из восьми треугольников, тогда 29 зонтов будут состоять из 232 треугольников.
Если на один треугольник требуется 1050 см2 ткани, то на 232 треугольника нужно будет 1050 · 232 = 243 600 см2.
Площадь ткани в рулоне равна 3500 · 80 = 280 000 см2.
Площадь ткани, ушедшей в обрезки, равна 280 000 — 243 600 = 36 400 см2.
Пусть 280 000 см2 — 100%, а 36 400 — х%. Составим и решим пропорцию:
Ответ: 13.
А вы тоже находите проблему из ничего, как Вася и Петя?)
Не можешь найти нужную задачу? Предложи свою! Наша группа в VK.
Вася нашёл площадь купола зонта как площадь поверхности сферического сегмента по формуле где R — радиус сферы, a h — высота сегмента. Рассчитайте площадь поверхности купола способом Васи. Число
округлите до 3,14. Ответ дайте в квадратных сантиметрах с округлением до целого.
Два друга Петя и Вася задумались о том, как рассчитать площадь поверхности зонта.
На первый взгляд зонт кажется круглым, а его купол напоминает часть сферы (сферический сегмент). Но если присмотреться, то видно, что купол зонта состоит из восьми отдельных клиньев, натянутых на каркас из восьми спиц (рис. 1). Сферическая форма в раскрытом состоянии достигается за счёт гибкости спиц и эластичности ткани, из которой изготовлен зонт.
Петя и Вася сумели измерить расстояние между концами соседних спиц а. Оно оказалось равно 38 см. Высота купола зонта h (рис. 2) оказалась равна 25 см, а расстояние d между концами спиц, образующих дугу окружности, проходящей через вершину зонта, — ровно 100 см.
1
Длина зонта в сложенном виде равна 25 см и складывается из длины ручки (рис. 3) и трети длины спицы (зонт в три сложения). Найдите длину спицы, если длина ручки зонта равна 6,2 см.
2
Поскольку зонт сшит из треугольников, рассуждал Петя, площадь его поверхности можно найти как сумму площадей треугольников. Вычислите площадь поверхности зонта методом Пети, если высота каждого равнобедренного треугольника, проведённая к основанию, равна 53,1 см. Ответ дайте в квадратных сантиметрах с округлением до десятков.
3
Вася предположил, что купол зонта имеет форму сферического сегмента. Вычислите радиус R сферы купола, зная, что (рис. 2). Ответ дайте в сантиметрах.
4
Рулон ткани имеет длину 35 м и ширину 80 см. На фабрике из этого рулона были вырезаны треугольные клинья для 29 зонтов, таких же, как зонт, который был у Пети и Васи. Каждый треугольник с учётом припуска на швы имеет площадь 1050 кв. см. Оставшаяся ткань пошла в обрезки. Сколько процентов ткани рулона пошло в обрезки?
Спрятать решение
Решение.
Воспользуемся значением R, полученным в предыдущем задании, тогда по формуле рассчитаем площадь поверхности купола
см2, округлив до целого, получим 9813 см2.
Ответ: 9813.
Решение практических задач ОГЭ. Математика. Зонт.
Учитель первой категории
МАОУ СОШ №61
Ветошкина В.А
г. Нижний Тагил
2021г.
C
h=25
А
R
Рис.1
о
d=100
Риc.2
- 1. 1Два друга Петя и Вася задумались о том, как рассчитать площадь поверхности зонта. На первый взгляд зонт кажется круглым, а его купол напоминает часть сферы (сферический сегмент). Но если присмотреться, то видно, что купол зонта состоит из восьми отдельных клиньев, натянутых на каркас из восьми спиц (рис. 1). Сферическая форма в раскрытом состоянии достигается за счёт гибкости спиц и эластичности ткани, из которой изготовлен зонт
Петя и Вася сумели измерить расстояние между концами соседних спиц а. Оно оказалось равно 38 см. Высота купола зонта h (рис. 2) оказалась равна 25 см, а расстояние d между концами спиц, образующих дугу окружности, проходящей через вершину зонта, — ровно 100 см.
- 1 . 1Длина зонта в сложенном виде равна 25 см и складывается из длины ручки (рис. 3) и трети длины спицы (зонт в три сложения). Найдите длину спицы, если длина ручки зонта равна 6,2 см.
- Решение.
- 1) Сколько сантиметров треть спицы ?
- 25 – 6,2 = 18,8 см
- 2) Найдем длину всей спицы.
- 18,8∙3 = 56,4 см
- Ответ: 56,4
Рис.3
Задание 2. 1Поскольку зонт сшит из треугольников, рассуждал Петя, площадь его поверхности можно найти как сумму площадей треугольников. Вычислите площадь поверхности зонта методом Пети, если высота каждого равнобедренного треугольника, проведённая к основанию, равна 53,1 см. Ответ дайте в квадратных сантиметрах с округлением до десятков.
- Решение.
- Высота h = 53,1 см, проведенная к основанию a = 38 см.
- Площадь каждого сегмента, равную:
- Sсег= 0,5ah
- Sсег= 0,5·38·53,1= 1008,9 см²
- Так как таких сегментов 8, то получаем полную площадь поверхности:
- 8Sсег = 8·1008,9 = 8071, 2см²
- 807/ 1 , 2 ≈ 8070
- Округляем до десятков, получаем 8070 кв. см.
- Ответ: 8070
h=53,1
a =38см
C
Задание 3. 1Вася предположил, что купол зонта имеет форму сферического сегмента. Вычислите радиус R сферы купола, зная, что ОС = R (рис. 2). Ответ дайте в сантиметрах
0,5 d=50
h=25
B
А
R-h=R-25
R
о
d=100
Риc.2
- Решение.
- Рассмотрим прямоугольный треугольник с катетами d / 2 = 0,5d =АВ и R-h =ВО, а гипотенузой R=АО.
- Рассмотрим по теореме Пифагора можно записать равенство: R²= (0,5d)² + ( R-h)²
- R² = 0,25d² + R²- 2Rh+ h²
- Решаем уравнение относительно R, имеем:
- R²=2500+ R² -50 R +625
- 50R= 3125
- R=62,5
- Ответ: 62,5
Задание 4. 1Вася нашёл площадь купола зонта как площадь поверхности сферического сегмента по формуле S = 2πRh , где R — радиус сферы, а h — высота сегмента. Рассчитайте площадь поверхности купола способом Васи. Число π округлите до 3,14. Ответ дайте в квадратных сантиметрах с округлением до целого.
- Решение. Подставим в формулу площади купола зонта числовые значения, получим:
- 𝑆 поверх. купола = 2πRh
- Значение R возьмём из задания №3. R = 62,5 см. h = 25 см, тогда S = 2· 3,14 ∙62,5 ∙25= 9812,5 ( см ² )
- Результат округлим до целого 9812/ ,5 ≈ 9813
- Ответ: 9813
Задание 5. 1Рулон ткани имеет длину 35 м и ширину 80 см. На фабрике из этого рулона были вырезаны треугольные клинья для 29 зонтов, таких же, как зонт, который был у Пети и Васи. Каждый треугольник с учётом припуска на швы имеет площадь 1050 кв. см. Оставшаяся ткань пошла в обрезки. Сколько процентов ткани рулона пошло в обрезки?
- Решение. Вычислим площадь ткани в кв. см, получим: S = 3500∙80 = 280 000 см²
- Площадь клиньев для 29 зонтов, равна:
- S= 29∙8∙1050 = 243 600 см²
- Площадь обрезков: 280 000 – 243 600 =
= 36 400 см²
- Что составляет: 36400 : 280000∙ 100%=13 .
- Ответ: 13
C
h=27
А
B
R
о
Рис.1
d=108
Риc.2
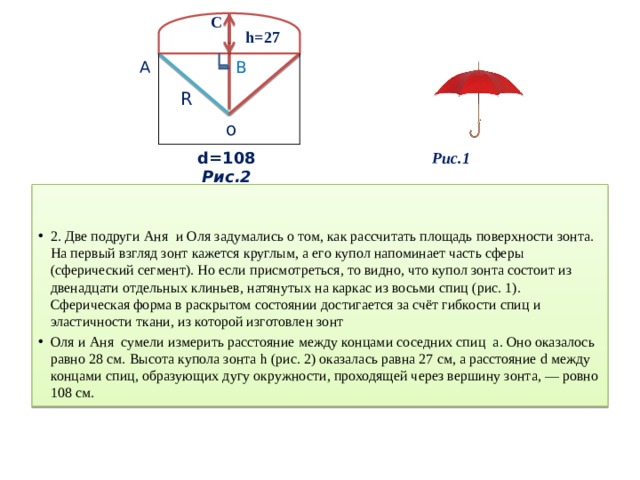
- 2. Две подруги Аня и Оля задумались о том, как рассчитать площадь поверхности зонта. На первый взгляд зонт кажется круглым, а его купол напоминает часть сферы (сферический сегмент). Но если присмотреться, то видно, что купол зонта состоит из двенадцати отдельных клиньев, натянутых на каркас из восьми спиц (рис. 1). Сферическая форма в раскрытом состоянии достигается за счёт гибкости спиц и эластичности ткани, из которой изготовлен зонт
- Оля и Аня сумели измерить расстояние между концами соседних спиц а. Оно оказалось равно 28 см. Высота купола зонта h (рис. 2) оказалась равна 27 см, а расстояние d между концами спиц, образующих дугу окружности, проходящей через вершину зонта, — ровно 108 см.
- 2.1. Длина зонта в сложенном виде равна 27 см и складывается из длины ручки (рис. 3) и трети длины спицы (зонт в три сложения). Найдите длину спицы, если длина ручки зонта равна 6,8 см.
- Решение: Длина зонта в сложенном виде вместе с длиной ручки равна 27 см. Надо вычесть длину ручки и результат умножить на три (т.к. спицы зонта сложились трижды) (27 – 6,8) · 3 =20,2∙ 3 = 60,6 (см) Ответ: 60,6
Рис.3
Задание №2 Поскольку зонт сшит из треугольников, рассуждала Оля, площадь его поверхности можно найти как сумму площадей треугольников. Вычислите площадь поверхности зонта методом Оли, если высота каждого равнобедренного треугольника, проведённая к основанию, равна 59 см. Ответ дайте в квадратных сантиметрах с округлением до десятков.
- Решение: h=59 см а = 28см Зонт сшит из 12 треугольников
- 𝑆 пов .= 0,5 𝑎·ℎ ∙ 12
- 𝑆 пов .= 0,5 𝑎·ℎ ∙ 12= = 0,5 ·28·59 ∙ 12 = 9912 ( см ² )
- Результат округлим до десятков 991/ 2 ≈ 9910 Ответ: 9910.
h = 59cм
а =28см
C
Задание №3 Аня предположила, что купол зонта имеет форму сферического сегмента. Вычислите радиус R сферы купола, зная, что ОС= R (рис. 2). Ответ дайте в сантиметрах
h=27
54
B
А
R
R-27
о
d=108
Риc.2
- Решение.
- Рассмотрим прямоугольный треугольник с катетами d / 2 = 0,5d= 54 и R-h = R-27, а гипотенузой R.
- Рассмотрим по теореме Пифагора можно записать равенство:
- R²= (0,5d)² + ( R-h)²
- R² = 54² + R²- 2R·27 +27²
- Решаем уравнение относительно R, имеем:
- R²= 2916 + R² -54 R +729
- 54R= 3645
- R=67,5
- Ответ: 67,5
Задание №4 Аня нашла площадь купола зонта как площадь поверхности сферического сегмента по формуле S=2πRh, где R- радиус сферы, а h-высота сегмента. Рассчитайте площадь поверхности купола способом Ани. Число π округлите до 3,14. Ответ дайте в квадратных сантиметрах с округлением до целого.
- Решение : 𝑆 поверх. купола = 2πRh Значение R возьмём из задания №3. R = 67,5 см. h = 27 см, тогда S = 2· 3,14 ∙67,5 ∙27=11445,3( см 2 ) Результат округлим до целого 11445/ ,3 ≈ 11445 Ответ: 11445
Задание №5 Рулон ткани имеет длину 20 м и ширину 90 см. На фабрике из этого рулона были вырезаны треугольные клинья для 15 зонтов, таких же, как зонт, который был у Оли и Ани. Каждый треугольник с учётом припуска на швы имеет площадь 850 кв. см. Оставшаяся ткань пошла в обрезки. Сколько процентов ткани рулона пошло в обрезки?
- Решение: Длина рулона ткани а=20м =2000см Ширина ткани b=90см. 1)Площадь рулона ткани S рулона= a·b S рулона= a·b = 2000·90 = 180000 ( см ² ) 2)Площадь ткани на все треугольники, а их 12 S всех треугольников = 850∙12·15= 153000(см ²) 180000 – 153000 =27000 кв.см 3) 180000 см² — 100% 27000 см² — Х% Х= 27000∙100 :180000 = 15% Ответ: 15
Литература
- Типовые экзаменационные варианты. Математика. ОГЭ 36 вариантов под редакцией И.В. Ященко, М. 2021 Сайт ФИПИ.
- Типовые экзаменационные варианты. Математика. ОГЭ 50 вариантов под редакцией И.В. Ященко, М. 2020 Сайт ФИПИ.
- Типовые экзаменационные варианты. Математика. ОГЭ 50 вариантов под редакцией И.В. Ященко, М. 2021 Сайт ФИПИ.
Версия для печати и копирования в MS Word
Вася нашёл площадь купола зонта как площадь поверхности сферического сегмента по формуле где R — радиус сферы, a h — высота сегмента. Рассчитайте площадь поверхности купола способом Васи. Число
округлите до 3,14. Ответ дайте в квадратных сантиметрах с округлением до целого.
Два друга Петя и Вася задумались о том, как рассчитать площадь поверхности зонта.
На первый взгляд зонт кажется круглым, а его купол напоминает часть сферы (сферический сегмент). Но если присмотреться, то видно, что купол зонта состоит из восьми отдельных клиньев, натянутых на каркас из восьми спиц (рис. 1). Сферическая форма в раскрытом состоянии достигается за счёт гибкости спиц и эластичности ткани, из которой изготовлен зонт.
Петя и Вася сумели измерить расстояние между концами соседних спиц а. Оно оказалось равно 38 см. Высота купола зонта h (рис. 2) оказалась равна 25 см, а расстояние d между концами спиц, образующих дугу окружности, проходящей через вершину зонта, — ровно 100 см.
Спрятать решение
Решение.
Воспользуемся значением R, полученным в предыдущем задании, тогда по формуле рассчитаем площадь поверхности купола
см2, округлив до целого, получим 9813 см2.
Ответ: 9813.
1
Длина зонта в сложенном виде равна 25 см и складывается из длины ручки (рис. 3) и трети длины спицы (зонт в три сложения). Найдите длину спицы, если длина ручки зонта равна 6,2 см.
2
Поскольку зонт сшит из треугольников, рассуждал Петя, площадь его поверхности можно найти как сумму площадей треугольников. Вычислите площадь поверхности зонта методом Пети, если высота каждого равнобедренного треугольника, проведённая к основанию, равна 53,1 см. Ответ дайте в квадратных сантиметрах с округлением до десятков.
3
Вася предположил, что купол зонта имеет форму сферического сегмента. Вычислите радиус R сферы купола, зная, что (рис. 2). Ответ дайте в сантиметрах.
4
Рулон ткани имеет длину 35 м и ширину 80 см. На фабрике из этого рулона были вырезаны треугольные клинья для 29 зонтов, таких же, как зонт, который был у Пети и Васи. Каждый треугольник с учётом припуска на швы имеет площадь 1050 кв. см. Оставшаяся ткань пошла в обрезки. Сколько процентов ткани рулона пошло в обрезки?