Как найти радиус сектора боковой поверхности - AvtoShod.ru

Как найти радиус сектора окружности

Круг — это часть плоскости, ограниченная окружностью. Центр данной окружности называется центром круга, а расстояние от центра до любой точки окружности — радиусом круга:

O — центр круга, OA — радиус круга.

Площадь круга

Площадь круга равна произведению числа π на квадрат радиуса. Формула нахождения площади круга:

где S — площадь круга, а r — радиус круга.

Так как диаметр круга равен удвоенному радиусу, то радиус равен диаметру, разделённому на 2:

Следовательно, формула нахождения площади круга через диаметр будет выглядеть так:

S = π(	D	) 2 = π	D 2	= π	D 2	.
2	2 2	4

Сектор круга. Площадь сектора

Сектор — это часть круга, ограниченная двумя радиусами и дугой. Два радиуса разделяют круг на два сектора:

Чтобы найти площадь сектора, дуга которого содержит n°, надо площадь круга разделить на 360 и полученный результат умножить на n.

Формула площади сектора:

S =	πr 2	· n =	πr 2 n	,
360	360

где S — площадь сектора. Выражение

можно представить в виде произведения

πr 2 n	= n ·	πr	·	r	,
360	180	2

где	nπr	— это длина дуги сектора.
180

Следовательно, площадь сектора равна длине дуги сектора, умноженной на половину радиуса:

где S — это площадь сектора, s — длина дуги данного сектора, r — радиус круга.

Сегмент. Площадь сегмента

Сегмент — это часть круга, ограниченная дугой и стягивающей её хордой. Любая хорда делит круг на два сегмента:

Площадь сегмента равна половине радиуса, умноженной на разность между дугой сегмента и половиной хорды двойной дуги.

Площадь сегмента AMB будет вычисляться по формуле:

где S — это площадь сегмента, r — радиус круга, s — длина дуги AB, а BC — длина половины хорды двойной дуги.

Как найти радиус окружности

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).

Основные понятия

Прежде чем погружаться в последовательность расчетов, важно понять разницу между понятиями.

Окружность — замкнутая плоская кривая, все точки которой равноудалены от центра, которая лежит в той же плоскости. Если говорить проще, то это замкнутая линия, как, например, обруч и кольцо.

Круг — множество точек на плоскости, которые удалены от центра на расстоянии равном радиусу. Иначе говоря, плоская фигура, ограниченная окружностью, как мяч и блюдце.

Радиус — это отрезок, который соединяет центр окружности и любую точку на ней. Общепринятое обозначение радиуса — латинская буква R.

Возможно тебе интересно узнать — как найти длину окружности?

Формула радиуса окружности

Определить способ вычисления проще, отталкиваясь от исходных данных. Далее рассмотрим девять формул разной степени сложности.

Если известна площадь круга

R = √ S : π, где S — площадь круга, π — это константа, которая выражает отношение длины окружности к диаметру, она всегда равна 3,14.

Если известна длина

R = P : 2 * π, где P — длина (периметр круга).

Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курс подготовки к ЕГЭ по математике (профиль).

Если известен диаметр окружности

R = D : 2, где D — диаметр.

Диаметр — отрезок, который соединяет две точки окружности и проходит через центр. Радиус всегда равен половине диаметра.

Если известна диагональ вписанного прямоугольника

R = d : 2, где d — диагональ.

Диагональ вписанного прямоугольник делит фигуру на два прямоугольных треугольника и является их гипотенузой — стороной, лежащей напротив прямого угла. Если диагональ неизвестна, теорема Пифагора поможет её вычислить:

d = √ a 2 + b 2 , где a, b — стороны вписанного прямоугольника.

Если известна сторона описанного квадрата

R = a : 2, где a — сторона.

Сторона описанного квадрата равна диаметру окружности.

Если известны стороны и площадь вписанного треугольника

R = (a * b * c) : (4 * S), где a, b, с — стороны, S — площадь треугольника.

Если известна площадь и полупериметр описанного треугольника

R = S : p, где S — площадь треугольника, p — полупериметр треугольника.

Полупериметр треугольника — это сумма длин всех его сторон, деленная на два.

Если известна площадь сектора и его центральный угол

R = √ (360° * S) : (π * α), где S — площадь сектора круга, α — центральный угол.

Площадь сектора круга — это часть S всей фигуры, ограниченной окружностью с радиусом.

Если известна сторона вписанного правильного многоугольника

R = a : (2 * sin (180 : N)), где a — сторона правильного многоугольника, N — количество сторон.

В правильном многоугольнике все стороны равны.

Скачать онлайн таблицу

У каждой геометрической фигуры много формул — запомнить все сразу бывает действительно сложно. В этом деле поможет регулярное решение задач и частый просмотр формул. Можно распечатать эту таблицу и использовать, как закладку в тетрадке или учебнике, и обращаться к ней по необходимости.

Площадь круга и его частей. Длина окружности и ее дуг

Основные определения и свойства

Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности

Часть окружности, расположенная между двумя точками окружности

Конечная часть плоскости, ограниченная окружностью

Часть круга, ограниченная двумя радиусами

Часть круга, ограниченная хордой

Выпуклый многоугольник, у которого все стороны равны и все углы равны

Около любого правильного многоугольника можно описать окружность

Фигура	Рисунок	Определения и свойства
Окружность
Дуга
Круг
Сектор
Сегмент
Правильный многоугольник

Окружность

Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности

Дуга

Часть окружности, расположенная между двумя точками окружности

Круг

Конечная часть плоскости, ограниченная окружностью

Сектор

Часть круга, ограниченная двумя радиусами

Сегмент

Часть круга, ограниченная хордой

Правильный многоугольник

Выпуклый многоугольник, у которого все стороны равны и все углы равны

Около любого правильного многоугольника можно описать окружность

Определение 1 . Площадью круга называют предел, к которому стремятся площади правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон.

Определение 2 . Длиной окружности называют предел, к которому стремятся периметры правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон.

Замечание 1 . Доказательство того, что пределы площадей и периметров правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон действительно существуют, выходит за рамки школьной математики и в нашем справочнике не приводится.

Определение 3 . Числом π (пи) называют число, равное площади круга радиуса 1.

Замечание 2 . Число π является иррациональным числом, т.е. числом, которое выражается бесконечной непериодической десятичной дробью:

Число π является трансцендентным числом, то есть числом, которое не может быть корнем алгебраического уравнения с целочисленными коэффициентами.

Формулы для площади круга и его частей

где R – радиус круга, D – диаметр круга

если величина угла α выражена в радианах

если величина угла α выражена в градусах

если величина угла α выражена в радианах

если величина угла α выражена в градусах

Числовая характеристика	Рисунок	Формула
Площадь круга
Площадь сектора
Площадь сегмента

Площадь круга

где R – радиус круга, D – диаметр круга

Площадь сектора

если величина угла α выражена в радианах

если величина угла α выражена в градусах

Площадь сегмента

если величина угла α выражена в радианах

если величина угла α выражена в градусах

Формулы для длины окружности и её дуг

где R – радиус круга, D – диаметр круга

если величина угла α выражена в радианах

если величина угла α выражена в градусах

Длина окружности

где R – радиус круга, D – диаметр круга

Длина дуги

если величина угла α выражена в радианах

если величина угла α выражена в градусах

Площадь круга

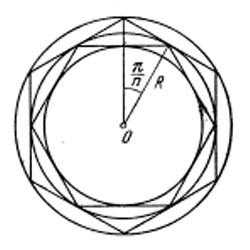
Рассмотрим две окружности с общим центром ( концентрические окружности ) и радиусами радиусами 1 и R , в каждую из которых вписан правильный n – угольник (рис. 1).

Обозначим через O общий центр этих окружностей. Пусть внутренняя окружность имеет радиус 1 .

Поскольку при увеличении n площадь правильного n – угольника, вписанного в окружность радиуса 1 , стремится к π , то при увеличении n площадь правильного n – угольника, вписанного в окружность радиуса R , стремится к числу πR 2 .

Таким образом, площадь круга радиуса R , обозначаемая S , равна

Длина окружности

то, обозначая длину окружности радиуса R буквой C , мы, в соответствии с определением 2, при увеличении n получаем равенство:

откуда вытекает формула для длины окружности радиуса R :

Следствие . Длина окружности радиуса 1 равна 2π.

Длина дуги

Рассмотрим дугу окружности, изображённую на рисунке 3, и обозначим её длину символом L(α), где буквой α обозначена величина соответствующего центрального угла.

В случае, когда величина α выражена в градусах, справедлива пропорция

из которой вытекает равенство:

В случае, когда величина α выражена в радианах, справедлива пропорция

из которой вытекает равенство:

Площадь сектора

Рассмотрим круговой сектор, изображённый на рисунке 4, и обозначим его площадь символом S (α) , где буквой α обозначена величина соответствующего центрального угла.

В случае, когда величина α выражена в градусах, справедлива пропорция

из которой вытекает равенство:

В случае, когда величина α выражена в радианах, справедлива пропорция

из которой вытекает равенство:

Площадь сегмента

Рассмотрим круговой сегмент, изображённый на рисунке 5, и обозначим его площадь символом S (α), где буквой α обозначена величина соответствующего центрального угла.

Поскольку площадь сегмента равна разности площадей кругового сектора MON и треугольника MON (рис.5), то в случае, когда величина α выражена в градусах, получаем

В случае, когда величина α выражена в в радианах, получаем

источники:

http://skysmart.ru/articles/mathematic/radius-okruzhnosti

http://www.resolventa.ru/demo/diaggia6.htm

Источник

Телом вращения называют пространственную фигуру, полученную в результате вращения некоторой плоской фигуры вокруг оси. Среди всех тел вращения выделяют цилиндр, конус и шар.

Цилиндром называют фигуру, полученную в результате вращения прямоугольника вокруг одной из его сторон (оси цилиндра).

Образующей цилиндра называют отрезок, соединяющий точки окружностей оснований цилиндра, и перпендикулярный диаметрам его оснований.

Высотой цилиндра называют перпендикуляр, заключенный между основаниями цилиндра.

На рисунке 9.66 прямая – ось вращения; – высота, – образующая цилиндра, полученного вращением прямоугольника вокруг стороны . Основание цилиндра – круг радиуса . Прямоугольник – осевое сечение цилиндра.

Объем цилиндра высоты находят по формуле:

$LaTeX formula: V=S_{o.}cdot h$ . (9.15)

Площадь основания цилиндра ( – радиус основания) находят по формуле:

$LaTeX formula: S_{o.}=pi r ^2$ . (9.16)

Площадь поверхности цилиндра находят по формуле:

$LaTeX formula: S_{n.}=2S_{o.}+S_{delta .}$ . (9.17)

Площадь боковой поверхности цилиндра находят по формуле:

$LaTeX formula: S_{delta .}=2pi r l$ , (9.18)

где – радиус основания, – высота, – образующая цилиндра.

Конусом называют фигуру, полученную в результате вращения прямоугольного треугольника вокруг одного из катетов (оси конуса).

Образующей конуса называют отрезок, соединяющий вершину конуса с точкой окружности основания конуса.

Высотой конуса называют перпендикуляр, соединяющий вершину конуса с центром его основания.

На рисунке 9.67 прямая – ось вращения; – высота конуса, – образующая конуса, – осевое сечение конуса, полученного вращением прямоугольного треугольника вокруг катета .

Усеченным конусом называют часть конуса, ограниченную его основанием и сечением, параллельным плоскости основания.

На рисунке 9.68 изображен усеченный конус.

Объем конуса высоты находят по формуле:

$LaTeX formula: V=frac{1}{3}S_{o.}cdot h$ . (9.19)

Площадь основания конуса ( – радиус основания) находят по формуле:

$LaTeX formula: S_{o.}=pi r^2$ . (9.20)

Площадь поверхности конуса находят по формуле:

$LaTeX formula: S_{n.}=2S_{o.}+S_{delta .}$ . (9.21)

Площадь боковой поверхности конуса находят по формуле:

$LaTeX formula: S_{delta .}=pi r l$ , (9.22)

где – радиус основания, – образующая конуса.

Объем усеченного конуса находят по формуле:

$LaTeX formula: V=frac{1}{3}pi h(r^2_1+r^2_2+r_1r_2)$ , (9.23)

где и – радиусы оснований, – высота.

Площадь боковой поверхности усеченного конуса находят по формуле:

$LaTeX formula: S_{delta .}=pi (r_1+r_2)l$ , (9.24)

где и – радиусы оснований, – высота, – образующая усеченного конуса.

Сферой называют фигуру, полученную в результате вращения полуокружности вокруг ее диаметра (рис. 9.69).

Шаром называют фигуру, полученную вращением полукруга вокруг его диаметра.

Сечение сферы плоскостью – окружность.

Сечение шара плоскостью – круг.

Сечение шара плоскостью, проходящей через центр шара, называют большим кругом (на рисунке 9.69 круг с центром в точке и радиусом ).

Касательной плоскостью к сфере (шару) называется плоскость, имеющая со сферой единственную общую точку (на рисунке 9.69 плоскость ). Эту точку называют точкой касания сферы и плоскости (на рисунке 9.69 точка ).

Касательная плоскость перпендикулярна радиусу сферы в точке касания.

Площадь сферы радиуса находят по формуле:

$LaTeX formula: S_{cphi .}=4pi R^2$ . (9.25)

Объем шара радиуса находят по формуле:

$LaTeX formula: V_{wapa}=frac{4}{3}pi R^3$ . (9.26)

Выпуклый многоугольник вписан в сферу, если все его вершины лежат на поверхности сферы, и описан около сферы, если все его стороны касаются поверхности сферы.

Сферическим (шаровым) сегментом называют часть сферы (шара), отсекаемую плоскостью.

Высотой шарового сегмента называют длину отрезка диаметра, перпендикулярного основанию шарового сегмента, расположенного между этим основанием и сферой (на рис. 9.70 ).

Шаровым сектором называют тело, полученное вращением кругового сектора вокруг одного из ограничивающих круговой сектор радиусов.

Высотой шарового сектора называют высоту части его сферической поверхности.

На рисунке 9.70 шаровой сектор получен в результате вращения кругового сектора вокруг радиуса .

Объем шарового сегмента находят по формуле:

$LaTeX formula: V_{c.}=pi h^2(R-frac{1}{3}h)$ . (9.27)

Площадь сферической поверхности находят по формуле:

$LaTeX formula: S_{n.}=2pi Rh$ , (9.28)

где – радиус шара; – высота сегмента.

Объем шарового сектора находят по формуле:

$LaTeX formula: V_{cekappa .}=frac{2}{3}pi R^2h$ , (9.29)

где – радиус шара; – высота сегмента.

Пример 1. Осевое сечение цилиндра – квадрат со стороной . Найдите объем и площадь поверхности цилиндра.

Решение. Так как осевое сечение квадрат (рис. 9.71), то , $LaTeX formula: r=frac{a}{2}$ .

По формулам 9.15 и 9.16 найдем объем цилиндра: $LaTeX formula: V=pi cdot frac{a^2}{4}cdot a=frac{pi a^3}{4}$ .

По формулам 9.16 , 9.17 и 9.18 найдем площадь поверхности цилиндра: $LaTeX formula: S_{n.}=frac{2pi a^2}{4}+frac{2pi a^2}{2}=frac{3pi a^2}{2}$ .

Ответ: ; .

Пример 2. Площадь боковой поверхности цилиндра равна , а объем его равен . Найдите высоту этого цилиндра.

Решение. Площадь боковой поверхности и объем цилиндра найдем по формулам 9.18 и 9.15 , где – радиус основания, – высота цилиндра.

Тогда согласно условию задачи запишем: $LaTeX formula: begin{cases} 2pi Rh=119, \ pi R^2h=7pi. end{cases}$

Разделим первое уравнение системы на второе и получим: $LaTeX formula: frac{2pi Rh}{pi R^2h}=frac{119}{7pi }$ , $LaTeX formula: frac{2}{R}=frac{17}{pi }$ , $LaTeX formula: R=frac{2pi }{17}$ .

Найдем из первого уравнения системы: $LaTeX formula: h=frac{119}{2pi R}=frac{119cdot 17}{2pi cdot 2pi }=frac{2023}{4pi ^2}$ .

Ответ: $LaTeX formula: frac{2023}{4pi ^2}$ .

Пример 3. Найдите объем и площадь поверхности конуса, осевым сечением которого является правильный треугольник со стороной см (рис. 9.72).

Решение. Так как см, а см, то из теоремы Пифагора: $LaTeX formula: h=sqrt{l^2-r^2}$ , (см).

По формулам 9.19 и 9.20 найдем объем конуса: $LaTeX formula: V=frac{1}{3}cdot pi cdot 3cdot 3=3pi$ ( $LaTeX formula: _{CM}\^3$ ).

По формулам 9.20 , 9.21 и 9.22 найдем площадь поверхности конуса: $LaTeX formula: S_{n.}=3pi +6pi =9pi$ ( $LaTeX formula: _{CM}\^2$ ).

Ответ: $LaTeX formula: _{CM}\^3$ ; $LaTeX formula: _{CM}\^2$ .

Пример 4. Радиус основания конуса равен , а угол при вершине в развертке его боковой поверхности равен $LaTeX formula: 90^{circ}$ . Определите объем конуса.

Решение. Рассмотрим конус радиуса и развертку его боковой поверхности – круговой сектор радиуса (рис. 9.73).

Найдем длину окружности в основании конуса: $LaTeX formula: C_{okappa p.}=2pi r=2sqrt{15}pi$ .

Найдем длину дуги в развертке боковой поверхности конуса: $LaTeX formula: C_{g.}=frac{2pi l}{360^{circ}}cdot 90^{circ}=frac{pi l}{2}$ .

Так как $LaTeX formula: C_{okappa p.}=C_{g.}$ , то $LaTeX formula: 2pi r=frac{pi l}{2}$ и .

Из теоремы Пифагора: , .

По формулам 9.19 и 9.20 найдем объем конуса: $LaTeX formula: V=frac{1}{3}cdot pi cdot 15cdot 15=75pi$ .

Ответ: .

Пример 5. Осевое сечение конуса – равнобокая трапеция с основаниями и . Образующая конуса равна . Найдите площадь боковой поверхности и объем конуса.

Решение. Имеем усеченный конус (рис. 9.74), радиусы оснований которого соответственно равны и . Зная образующую конуса , найдем его высоту: $LaTeX formula: h=sqrt{l^2-(r_1-r_2)^2}$ , .

По формуле 9.24 найдем площадь боковой поверхности конуса: $LaTeX formula: S_{delta .}=20sqrt{7}pi$ .

По формуле 9.23 найдем объем конуса:

$LaTeX formula: V=frac{1}{3}pi 2sqrt{7}(64+4+16)=56sqrt{7}pi$ .

Ответ: ; .

Пример 6. Периметр правильного шестиугольника, все вершины которого лежат на поверхности шара, равен . Объем шара равен . Найдите расстояние от центра шара до плоскости шестиугольника.

Решение. Найдем сторону правильного шестиугольника, зная его периметр: . Так как радиус окружности, описанной около правильного шестиугольника, равен его стороне, то на рисунке 9.75 .

Объем шара находят по формуле 9.26 .

Так как , то $LaTeX formula: 36pi =frac{4}{3}pi R^3$ , $LaTeX formula: 9=frac{1}{3}R^3$ , , .

Из теоремы Пифагора: $LaTeX formula: d=sqrt{R^2-r^2}$ , .

Ответ: .

Пример 7. Сторона квадрата, описанного около шара, равна . Найдите площадь сферической поверхности, отсекаемой плоскостью квадрата от шара, если радиус шара равен (рис. 9.76).

Решение. 1. Найдем диагональ квадрата, зная его сторону: , . Поскольку сечение шара плоскостью – круг, а квадрат описан около этого круга, то радиус сечения равен: $LaTeX formula: r=frac{d}{2}$ , .

2. Из теоремы Пифагора: $LaTeX formula: l=sqrt{R^2-r^2}$ , .

3. Найдем высоту сферической поверхности:

, .

4. По формуле 9.28 найдем площадь сферической поверхности:

$LaTeX formula: S_{n.}=2pi Rh$ , $LaTeX formula: S_{n.}=10pi (5-sqrt{17})$ .

Ответ: .

Пример 8. Равнобедренная трапеция с основаниями см и см и острым углом $LaTeX formula: 60^{circ}$ вращается вокруг меньшего основания. Вычислите поверхность полученной фигуры вращения.

Решение. Рассмотрим равнобедренную трапецию с основаниями см и см (рис. 9.77). Вращая трапецию вокруг основания , получим тело, боковая поверхность которого состоит из боковой поверхности цилиндра и боковой поверхности двух равных конусов: $LaTeX formula: S_{n.}=S_{delta .}+2S_{delta .kappa .}$ . В трапеции из вершин и проведем высоты и . Тогда $LaTeX formula: BN=CM=R_{v.}=R_{kappa .}=h_{mp.}$ .

Рассмотрим прямоугольный треугольник : $LaTeX formula: angle BAN=60^{circ}$ , $LaTeX formula: AN=frac{1}{2}(AD-NM)=frac{1}{2}cdot 1=frac{1}{2}$ (см),

тогда (см) и $LaTeX formula: BN=sqrt{1^2-left ( frac{1}{2} right )^2}=frac{sqrt{3}}{2}$ (см).

Согласно формуле $LaTeX formula: S_{delta .v.}=2pi R_{v.}l_{v.}$ получим: $LaTeX formula: S_{delta .v.}=2pi cdot frac{sqrt{3}}{2}cdot 13=13sqrt{3}pi$ ( $LaTeX formula: _{CM}\^2$ ).

Согласно формуле $LaTeX formula: S_{delta .kappa .}=pi R_{kappa .}l_{kappa .}$ получим: $LaTeX formula: S_{delta .kappa .}=pi frac{sqrt{3}}{2}cdot 1=frac{sqrt{3}pi }{2}$ ( $LaTeX formula: _{CM}\^2$ ).

Найдем площадь поверхности тела вращения: $LaTeX formula: S_{n.}=13sqrt{3}pi +2cdot frac{sqrt{3}pi }{2}=14sqrt{3}pi$ ( $LaTeX formula: _{CM}\^2$ ).

Ответ: $LaTeX formula: _{CM}\^2$ .

1. В цилиндре умейте определять: радиус основания, высоту, образующую, осевое сечение.

2. В конусе умейте определять: радиус основания, высоту, образующую, осевое сечение.

3. Различайте шар и сферу (поверхность шара). Умейте определять: 1) центр, радиус и диаметр сферы; 2) в шаре: центр, радиус, диаметр, сечение, шаровой сегмент и шаровой сектор.

Источник

Информация по назначению калькулятора

Сектор круга — это часть окружности внутри круга, состоящая из дуги вместе с ее двумя радиусами. Часть окружности (также известная как дуга) и 2 радиуса окружности встречаются в обеих конечных точках дуги, образуя сектор. Форма сектора круга выглядит как кусочек пиццы или пирога. В геометрии круг — одна из самых совершенных фигур. Форма сектора окружности — самая простая форма в геометрии. У него есть свои собственные различные части. Например, диаметр, радиус, окружность, сегмент, сектор.

Круг разделен на два сектора, и разделенные части известны как второстепенные сектора и главные сектора.

Большая часть круга является основным сектором, в то время как меньшая часть является второстепенным сектором.

В случае полукругов окружность делится на два сектора одинакового размера.

2 радиуса встречаются в части окружности круга, известной как дуга, образуя сектор окружности.

Онлайн калькулятор предназначен для нахождения параметров сектора круга, таких как:

Площадь сектора

— это объем пространства, занимаемого в пределах границы сектора круга. Сектор всегда начинается с центра круга. Полукруг также является сектором круга, в данном случае круг имеет два сектора одинакового размера.
Можно найти зная радиус и центральный угол в градусах (Ssek = ( α / 360° ) * πr²)

Длина дуги

— находится путем умножения радиуса на центральный угол сектора в радианах (L = r * α)

Радиус
Периметр сектора

— равен сумме длины дуги и двум радиусам (Psek = L + r + r)

Центральный угол сектора в градусах и радианах

Источник

Радиус конуса – Как найти радиус основания конуса чему равен радиус если известна площадь Наука Другое

Конус | LAMPA — онлайн-учебник, который каждый может улучшить

Конус — это тело, которое получается при объединении всех отрезков, соединяющих точки круга (основание конуса) с вершиной конуса.

Прямой конус — это конус, вершина которого лежит на прямой, перпендикулярной основанию и проходящей через центр основания. Эта прямая называется осью прямого конуса.

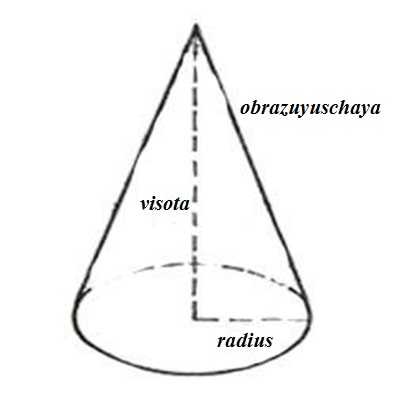
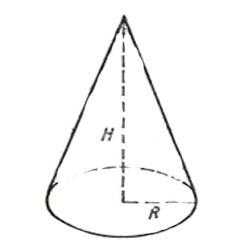
Высота конуса — это отрезок, проведенный из вершины конуса к основанию перпендикулярно основанию конуса. Отрезок, который соединяет вершину конуса с окружностью в основании, называется образующей конуса.

В задачах ЕГЭ рассматривается в основном прямой конус.

Прямой конус можно получить, если из бумажного круга вырезать сектор (с любым углом от 000 до 2π2pi2π), потом свернуть его в рупор, склеить по разрезу, а круглое отверстие закрыть кругом.

Если lll — длина образующей конуса, hhh — высота конуса, а rrr — радиус основания конуса, то

Объем конуса: V=13πr2hV=fracpi r^2hV=31πr2h,
Площадь боковой поверхности конуса: Sбок=πrlS_=pi rlSбок=πrl,
Площадь полной поверхности: S=πr(r+l)S=pi r(r+l)S=πr(r+l),
Образующая конуса: l=h3+r2l=sqrtl=h3+r2.

Заметим, что формула объема конуса очень похожа на формулу объема пирамиды. Это следует из того, что конус — это, по сути, та же пирамида, только вместо многоугольника в основании находится круг.

Формула для образующей конуса следует из теоремы Пифагора. Она является гипотенузой прямоугольного треугольника, катеты которого — это высота конуса и радиус основания конуса. Поэтому также верны формулы: h=l2−r2h=sqrth=l2−r2 и r=l2−h3r=sqrtr=l2−h3.

Формулу площади боковой поверхности можно получить, если рассмотреть развертку его боковой поверхности на плоскость. Она представляет собой сектор круга радиуса lll. При развертке вершина конуса переходит в центр круга, образующая — в его радиус, а окружность основания — в дугу сектора. Длина дуги сектора равна длине окружности основания конуса: 2πr2pi r2πr. Обозначим радианную меру угла сектора через αalphaα. Тогда длина его дуги равна αlalpha lαl, а площадь равна 12αl2frac alpha l^221αl2. Тогда αl=2πralpha l=2pi rαl=2πr. Значит, α=2πrlalpha =fracα=l2πr. Тогда площадь сектора равна 12⋅2πrl⋅l2=πrlfraccdot frac cdot l^2=pi rl21⋅l2πr⋅l2=πrl.

Пользуясь формулами, решите следующие задачи:

Как найти образующую конуса

Задание.
Как найти образующую конуса, если диаметр его основания равен 12 см, а высота равна 8 см.

Решение.
Изобразим схематически конус, на котором обозначим его высоту, радиус основания и образующую. Образующая конуса соединяет его вершину с одной из точек на окружности основания конуса. Радиус также соединяет центр окружности с любой из точек на этой окружности. Поэтому можем изобразить радиус и высоту на рисунке так, как нам будет удобно использовать их для решения задачи. Пусть концы радиуса и образующей совпадают.

Из рисунка хорошо видно, что из высоты, радиуса и образующей получается прямоугольный треугольник, к которому можно применить теорему Пифагора. Запишем уравнение для данного треугольника:

Значение высоты известно из условия, радиус можно найти через диаметр. Таким образом, вычислим значение образующей.
Итак, найдем длину радиуса, зная, что диаметр равен 12 см:
(см).
Теперь подставим известные значения в теорему Пифагора:

Ответ. 10 см.

Как найти радиус основания конуса?

Ответ оставил Гость

Площадь поверхности конуса

R — радиус основания конуса

H — высота

L — образующая конуса

Формула площади боковой поверхности конуса, через радиус (

Формула площади боковой поверхности конуса, через радиус (R) и высоту (H), (S_бок):

Обновлено: 25 мая 2017

Конус [wiki.eduVdom.com]

Конусом ( прямым круговым конусом ) называется тело, состоящее из круга ( основания конуса ), точки, не лежащей в плоскости этого круга ( вершины конуса ), и всех отрезков, соединяющих вершину конуса с точками основания.

Конус является телом вращения.

Отрезки, соединяющие вершину конуса с точками окружности основания, называются образующими конуса.

Конус — тело, которое ограничено конической поверхностью и плоскостью, на которой лежат концы образующих конической поверхности.

Коническая поверхность — поверхность, которая образуется движением отрезка, один из концов которого неподвижен, а другой перемещается на плоскости вдоль некоторой кривой. Отрезки называют образующими конической поверхности, а кривую – направляющей. Неподвижная точка – вершина конической поверхности.

Боковая поверхность конуса — часть конической поверхности, ограниченная плоскостью.

Основание конуса — часть плоскости, отсекаемая боковой поверхностью конуса.

Конус называется прямым, если прямая, соединяющая вершину конуса с центром основания, перпендикулярна плоскости основания (См.Рис.1). В противном случае, конус называется наклонным. В школьном курсе изучается прямой круговой конус.

Круговой конус

Прямой круговой конус ( просто конус ) — круговой конус, у которого прямая, соединяющая вершину конуса с центром круга, лежащего в основании, перпендикулярна плоскости основания.

Ось конуса — прямая, проходящая через вершину конуса и центр основания конуса.

Высота конуса — отрезок оси конуса, соединяющий вершину конуса с центром основания.

Конус можно рассматривать как тело, полученное вращением прямоугольного треугольника вокруг прямой, содержащей его катет.

Образующие конуса совпадают с образующими конической поверхности.

Сечение конуса плоскостью, проходящей через его ось, называется осевым сечением. Плоскость, проходящая через образующую конуса и перпендикулярная осевому сечению, проведенному через эту образующую, называется касательной плоскостью конуса. См.Рис.2

Развёртка боковой поверхности конуса — круговой сектор, радиус которого равен образующей конуса, а длина дуги сектора равна длине окружности основания конуса.

Площадь боковой поверхности ( круглого ) конуса равна произведению половины длины окружности основания (C) на образующую (l): $$S_=fraccdot Cl=picdot rl$$ , где r – радиус основания, l – длина образующей.

Площадь полной поверхности конуса — сумма площадей основания конуса и его боковой поверхности, которая записывается формулой: $$S_=picdot r(l+r)$$ , где r — радиус основания, l — длина образующей.

Объем всякого конуса равен трети произведения площади основания (S) на высоту ( h): $$V=fraccdot Sh$$ Объем круглого конуса: $$V=fraccdot Sh=fraccdotpi r^2 cdot h$$

Усеченный конус – это часть конуса, ограниченная его основанием и сечением, параллельным плоскости основания. См.Рис.3.

Формулы для усечённого конуса (См.Рис.4): $$ S_=picdot lcdot (R+r) \ S_=S_+pi(R^2+r^2) \ V=fracpicdot h(R^2+Rcdot r+r^2) $$

Пример 1. Высота конуса равна 4 , а длина образующей — 5. Найдите диаметр основания конуса.

Видео-решение.

Объем конуса — формула, пример расчета

Чтобы найти объем конуса необходимо произвести дополнительные построения.

Построим вписанную в конус правильную n-угольную пирамиду и опишем вокруг данного конуса правильную n-угольную пирамиду.
Вписанная пирамида содержится в конусе. Из этого следует, что ее объем не больше объема конуса.
Описанная пирамида содержит конус, а это значит, что ее объем не меньше объема конуса.

Впишем в основание вписанной пирамиды окружность.
Если радиус вписанного правильного n-угольника равен R, то радиус вписанной в него окружности будет равен:

Объем вписанной пирамиды вычисляется по формуле:

где S – основание пирамиды.
Площадь данного круга вычисляется по формуле:
Площадь основания вписанной пирамиды не меньше площади круга, содержащегося в ней
Поэтому утверждение, что объем вписанной в конус пирамиды не меньше верно.
А следовательно, мы может утверждать, что объем конуса, содержащий эту пирамиду будет больше или равен
V≥

Теперь опишем окружность вокруг основания описанной вокруг конуса пирамиды.
Радиус этой окружности будет равен:

Площадь данного круга вычисляется по формуле:
Основание описанной пирамиды содержится в круге описанном вокруг него. Поэтому площадь основания пирамиды не больше
Поэтому утверждение,что объем описанной пирамиды не больше верно.
А следовательно, мы может утверждать, что объем конуса, содержащий в эту пирамиду будет меньше или равен

Два полученных неравенства равны при любом n. Если то
Тогда из первого неравенства следует, что V≥
Из второго неравенства

Отсюда следует, что

Объем конуса равен одной трети произведения радиуса на высоту.

1)полукруг свернут в виде боковой поверхности конуса. Радиус основания конуса равен 5 см. Найдите объем конуса

Мне кажется то, посмотри этот документ <a href=»/» rel=»nofollow» title=»15907216:##:doc915_doc»>[ссылка заблокирована по решению администрации проекта]</a>

Привет, Настюшка, этот человек занимается педофилией, развращает мою 14-и летнюю дочь. Распространяет видео полового акта с ней.. Вскоре её буду осуждать на «Пусть говорят». Пожалуйста, сообщи ей об этом… <a rel=»nofollow» href=»http://vk.com/im?sel=173948305″ target=»_blank»>http://vk.com/id403649</a> Спасибо, удачи тебе

Здесь обсуждали нечто подобное <a href=»/» rel=»nofollow» title=»15907216:##:post-201334_102″>[ссылка заблокирована по решению администрации проекта]</a>

Это с форума, но должно помочь <a href=»/» rel=»nofollow» title=»15907216:##:title-401773_901″>[ссылка заблокирована по решению администрации проекта]</a>

Настя, не тупи. Задача седьмого класса.

если радиус основания равен 5, то длина окружности основания равен 2х5хПИ=31.4 Эта длина окружности соответствует длине полуокружности из которой образовался конус, значит ее радиус 31,4ПИ=10. Радусу полуокружности соответствует образующая конуса. Стало быть его высота равна корень из 10в2-5в2=8,66. объем конуса 13SH= 13хПИх25х8,66=226,72

Объём конуса

Площадь основания S_осн =
Высота h =

Через радиус и другие параметры

=
=

Как найти радиус основания конуса?

1)Если вам известны объем V и высота конуса H, выразите его радиус основания R из формулы V=1/3∙πR²H. Получите: R²=3V/πH, откуда R=√(3V/πH)
. 2) Если вам известны площадь боковой поверхности конуса S и длина его образующей L, выразите радиус R из формулы: S=πRL. Вы получите R=S/πL.
3)Следующие способы нахождения радиуса основания конуса базируются на утверждении, что конус образован при вращении прямоугольного треугольника вокруг одного из катетов к оси. Так, если вам известны высота конуса H и длина его образующей L, то для нахождения радиуса R вы можете воспользоваться теоремой Пифагора: L²=R²+H². Выразите из данной формулы R, получите: R²=L²–H² и R=√(L²–H²).
4)Используйте правила соотношений между сторонами и углами в прямоугольном треугольнике. Если известны образующая конуса L и угол α между высотой конуса и его образующей, найдите радиус основания R, равный одному из катетов прямоугольного треугольника, по формуле: R=L∙sinα.
5)Если известны образующая конуса L и угол β между радиусом основания конуса и его образующей, найдите радиус основания R по формуле: R=L∙cosβ. Если известны высота конуса H и угол α между его образующей и радиусом основания, найдите радиус основания R по формуле: R=H∙tgα.
6) Пример: образующая конуса L равна 20 см и угол α между образующей и высотой конуса равен 15º. Найдите радиус основания конуса. Решение: В прямоугольном треугольнике с гипотенузой L и острым углом α противолежащий этому углу катет R вычисляется по формуле R=L∙sinα. Подставьте соответствующие значения, получите: R=L∙sinα=20∙sin15º. Sin15º находится из формул тригонометрических функций половинного аргумента и равен 0,5√(2–√3). Отсюда катет R=20∙0,5√(2–√3)=10√(2–√3)см. Соответственно, радиус основания конуса R равен 10√(2–√3)см.
7)Частный случай: в прямоугольном треугольнике катет, противолежащий углу в 30º, равен половине гипотенузы. Таким образом, если известны длина образующей конуса и угол между его образующей и высотой равен 30º, то найдите радиус по формуле: R=1/2L.

Источник

Конус — тело вращения, которое получается в результате вращения прямоугольного треугольника вокруг его катета.

Треугольник (POA) вращается вокруг стороны (PO).

(PO) — ось конуса и высота конуса.

(P) — вершина конуса.

(PA) — образующая конуса.

Круг с центром (O) — основание конуса.

(AO) — радиус основания конуса.

Осевое сечение конуса — это сечение конуса плоскостью, которая проходит через ось (PO) конуса.

Осевое сечение конуса — это равнобедренный треугольник.

(APB) — осевое сечение конуса.

∡PAO=∡PBO

— углы между образующими и основанием конуса.

Для конуса построим развёртку боковой поверхности. Это круговой сектор.

Сектор имеет длину дуги, равную длине окружности в основании конуса

2πR

, угол развёртки боковой поверхности

В конусе нельзя обозначить угол развёртки.
На развёртке конуса нельзя обозначить высоту и радиус конуса.

Образующая конуса (l) является радиусом сектора.

Таким образом, боковая поверхность конуса является частью полного круга с радиусом (l):

Длина дуги также является частью длины полной окружности с радиусом (l), но в то же время длина дуги — это длина окружности основания конуса с радиусом (R).

Сравним выражения длины дуги и выразим

через (R):

2πl⋅α360°=2πR;α=2πR⋅360°2πl=R⋅360°l.

Получаем ещё одну формулу боковой поверхности конуса; не используется угол развёртки боковой поверхности:

Sбок.=πl2⋅R⋅360°360°⋅l=πRl

Если провести сечение конуса плоскостью, перпендикулярной оси конуса, то эта плоскость разбивает конус на две части, одна из которых — конус, а другую часть называют усечённым конусом.

Также усечённый конус можно рассматривать как тело вращения, которое образовалось в результате вращения прямоугольной трапеции вокруг боковой стороны (которая перпендикулярна к основанию трапеции) или в результате вращения равнобедренной трапеции вокруг высоты, проведённой через серединные точки оснований трапеции.

OO1

— ось конуса и высота конуса.

Круги с центрами (O) и

— основания усечённого конуса.

(AO) и

A1O1

— радиусы оснований конуса.

Осевое сечение конуса — это сечение конуса плоскостью, которая проходит через ось

OO1

конуса.

Осевое сечение конуса — это равнобедренная трапеция.

AA1B1B

— осевое сечение конуса.

Боковая поверхность определяется как разность боковой поверхности данного конуса и отсечённого конуса:

Sбок.=πR⋅PA−πr⋅PA1=πR⋅PA1+AA1−πr⋅PA1==πR⋅PA1+πR⋅AA1−πr⋅PA1==πR⋅l+πR−πr⋅PA1.

Так как

ΔPAO∼ΔPA1O1

, то стороны их пропорциональны:

PAPA1=Rr;l+PA1PA1=Rr;r⋅l+PA1=R⋅PA1;rl=R⋅PA1−r⋅PA1;PA1⋅R−r=rl;PA1=rlR−r.

Таким образом получаем формулу боковой поверхности усечённого конуса, которая содержит радиусы оснований и образующую усечённого конуса:

Sбок.=πRl+π⋅PA1⋅R−r=πRl+π⋅rlR−r⋅R−r;Sбок.=πRl+πrl=πl⋅R+r.

Источник

Как найти радиус сектора окружности

Площадь круга

Сектор круга. Площадь сектора

Сегмент. Площадь сегмента

Как найти радиус окружности

Основные понятия

Формула радиуса окружности

Если известна площадь круга

Если известна длина

Если известен диаметр окружности

Если известна диагональ вписанного прямоугольника

Если известна сторона описанного квадрата

Если известны стороны и площадь вписанного треугольника

Если известна площадь и полупериметр описанного треугольника

Если известна площадь сектора и его центральный угол

Если известна сторона вписанного правильного многоугольника

Скачать онлайн таблицу

Площадь круга и его частей. Длина окружности и ее дуг

Основные определения и свойства

Формулы для площади круга и его частей

Формулы для длины окружности и её дуг

Площадь круга

Длина окружности

Длина дуги

Площадь сектора

Площадь сегмента

Информация по назначению калькулятора

Онлайн калькулятор предназначен для нахождения параметров сектора круга, таких как:

Радиус конуса – Как найти радиус основания конуса чему равен радиус если известна площадь Наука Другое

Конус | LAMPA — онлайн-учебник, который каждый может улучшить

Как найти образующую конуса

Как найти радиус основания конуса?

Площадь поверхности конуса

Конус [wiki.eduVdom.com]

Объем конуса — формула, пример расчета

1)полукруг свернут в виде боковой поверхности конуса. Радиус основания конуса равен 5 см. Найдите объем конуса

Объём конуса

Через радиус и другие параметры

Теория

Объём конуса через площадь основания и высоту

Формула

Пример

Объём конуса через образующую и радиус

Формула

Пример

Объём конуса через радиус и высоту

Формула

Пример

Объём конуса через угол раствора (α) и радиус

Формула

Пример

Объём конуса через угол β и радиус

Формула

Пример

Объём конуса через угол γ и радиус

Формула

Пример

Как найти радиус основания конуса?

Не пропустите также: