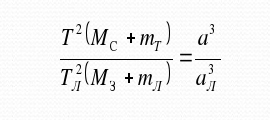Как найти радиус планеты не зная массы

How to find the radius of a satellite not knowing the mass:

If I know the

• semi-major axis,
• density of the planet, and
• orbital period..

how can I find the radius of the satellite? I can’t think of any formula to use.

I have a hunch that you’ve misunderstood the question, and that it asks for the radius of the planet not the artificial satellite, and that’s certainly doable. Otherwise, why would the planet’s density be a given?

The equation that links semi-major axis, mass of the planet, and orbital period is:

$$T=2 pi sqrt{frac{a^3}{GM}} $$

where $G$ is the gravitational constant 6.674E-11 m^3 s^-2 kg^-1.

Moving things around we get

$$frac{4 pi^2 a^3}{T^2G} = M $$

Density is mass per volume, or:

$$rho = frac{M}{frac{4}{3} pi R^3} = frac{3M}{4 pi R^3}$$

Moving that around we get

$$R = left(frac{3M}{4 rho pi}right)^{1/3}$$

Put in the earlier result for $M$, we get

$$R = a left(frac{3 pi}{rho T^2G}right)^{1/3}$$

For Earth’s average density, Wikipedia says 5514 kg/^3, for its radius, try 6,371,000. meters. For the ISS at 400 km (400,000 meters) above the Earth, use 92.5 minutes (5550 sec). It should all work out nicely!

The reason this works with average density, even though Earth’s density is higher in the core than the surface is the application of Newton’s shell theorem.

Вот такая задача. Есть планета, для простоты — сферическая, не вращающаяся, по составу однородная. Масса планеты [math]M[/math] известна ([math]M=frac{ 4 }{ 3 } cdot pi R^{3} cdot rho_ {R}[/math], где [math]R[/math] — радиус планеты, [math]rho _{R}[/math] — средняя плотность планеты). Коэффициент сжимаемости [math]beta[/math] материала, из которого сделана планета, известен ([math]beta = frac{ 1 }{ rho } cdot frac{ d rho }{ dP }[/math], где [math]rho[/math] — плотность, [math]P[/math] — давление). Плотность наружного слоя [math]rho _{0}[/math] — плотность при нулевом давлении — известна (ее, наверное, удобно за единицу принять). Очевидно, что этих данных достаточно, чтобы найти радиус планеты [math]R[/math]. Но вот как его найти — ума не приложу.
Понятно, что на расстоянии [math]r[/math] от центра планеты ([math]r<R[/math]) давление от вышележащих слоев [math]P_{r} = frac{ g_{r}left( M — M_{r} right) }{ 4 pi r^{2} }[/math], где [math]g_{r}[/math] — ускорение свободного падения на глубине [math]R-r[/math], [math]M_{r}[/math] — масса сферы с радиусом [math]r[/math]. [math]M_{r}=frac{ 4 }{ 3 } cdot pi r^{3} cdot rho _{r}[/math], [math]g_{r}=frac{ G cdot M_{r} }{ r^{2} }= frac{ 4 }{ 3 } cdot G pi r cdot rho _{r}[/math], где [math]rho _{r}[/math] — средняя плотность сферы с радиусом [math]r[/math], [math]G[/math] — гравитационная постоянная. Отсюда [math]P_{r}=frac{ 4G pi rho _{r}(R^{3} rho _{R}-r^{3} rho _{r}) }{ 9r }[/math]. А как же [math]P_{r}[/math], [math]rho _{R}[/math] и [math]rho _{r}[/math] выразить через [math]beta[/math]? Никто не подскажет?

Характеристики планет Солнечной системы были известны еще в средневековье, во времена Кеплера и Галилея. То есть, массу планет приблизительно можно было определить даже простыми методами и инструментами. В современной астрономии есть несколько методов расчета характеристик планет, звезд, скоплений и галактик.

Интересный факт: 99,9% всей массы Солнечной системы сосредоточена в самом Солнце. На все планеты вместе взятые приходится не более 0,01%. При этом из этих 0,01%, в свою очередь, 99% массы приходится на газовые гиганты (в том числе 90% только на Юпитер и Сатурн).

Рассчитываем массу Земли и Луны

Чтобы измерить массу планет солнечной системы, проще всего в первую очередь найти значения для Земли. Как мы помним, ускорение свободного падения определяется по формуле F=mg, где m – масса тела, а F – действующая на него сила.

Параллельно вспоминаем универсальный закон всемирного тяготения Ньютона:

Сопоставив эти две формулы, и зная значение гравитационной постоянной 6,67430(15)·10−11 м³/(кг·с²), можно рассчитать массу Земли. Ускорение свободного падения на Земле мы знаем, 9,8 м/с2, радиус планеты тоже. Подставив все данные на выходе получим приблизительно 5,97 х 10²⁴ кг.

Зная массу Земли, мы легко рассчитает параметры по другим объектам Солнечной системы – Луна, планеты, Солнце и так далее. С Луной вообще все довольно просто. Здесь достаточно учесть, что расстояния от центров тел до центра масс соотносятся обратно их массам. Подставив эти цифры для Земли и ее спутника получим массу Луны 7.36 × 10²² килограмма.

Перейдем теперь к методикам измерения массы планет земной группы – Меркурий, Венера, Марс. После чего рассмотрим газовые гиганты, и в самом конце – экзопланеты, звезды и галактики.

Общие методики определения масс планет

Наиболее классический способ, как узнать массу планет – расчет при помощи формул третьего закона Кеплера. Он гласит, что квадраты периодов обращения планет соотносятся так же, как кубы больших полуосей орбит. Ньютон немного уточнил этот закон, внеся в формулу массы небесных тел. На выходе получилась такая формула –

Таким способом можно найти массу всех планет Солнечной системы и самого Солнца.И периоды обращения, и большие полуоси орбит планет Солнечной системы легко измеряются астрономическими методиками, доступными даже без сложных инструментов. А так как массу Земли мы уже рассчитали, можно все цифры подставить в формулу и найти конечный результат.

В отношении же экзопланет и других звезд (но только двойных) в астрономии обычно применяется метод анализа видимых возмущений и колебаний. Он основан на том факте, что все массивные тела “возмущают” орбиты друг друга.

Такими расчетами были открыты планеты Нептун и Плутон, еще до их визуального обнаружения, как говорят “на кончике пера”.

Значения масс планет Солнечной системы

Итак, мы разобрались с общими методиками расчета масс разных небесных тел и посчитали значения для Луны, Земли и Галактики. Давайте теперь составим рейтинг планет нашей системы по их массе.

Возглавляет рейтинг с наибольшей массой планет Солнечной системы – Юпитер, которому не хватило одного порядка чтобы наша система стала двойной. Еще чуть-чуть и у нас могло быть два Солнца, второе вместо Юпитера. Итак, масса этого газового гиганта равняется 1,9 × 10²⁷ кг.

Интересно, что Юпитер – единственная планета нашей системы, центр масс вращения с Солнцем которой расположен вне поверхности звезды. Он отстоит примерно на 7% расстояния между ними от поверхности Солнца.

Вторая по массе планета – Сатурн, его масса 5,7 × 10²⁶ кг. Следующим идет Нептун – 1 × 10²⁶. Четвёртая по массе планета, газовый гигант Уран, масса которого – 8,7 × 10²⁵ кг.

Далее идут планеты земной группы, каменистые тела, в отличие от газовых гигантов с их большим радиусом и относительно малой плотностью.

Самой тяжелой из этой группы является наша планета, ее массу мы уже рассчитали. Далее идет Венера, масса этой планеты равняется 4,9 × 10²⁴ кг. После нее в рейтинге идет Марс, он почти в 10 раз легче – 6,4 × 10²³кг. И замыкает его, как планета самой маленькой массы, Меркурий – 3,3 × 10²³кг. Что интересно, Меркурий даже легче, чем два спутника в Солнечной системе – Ганимед и Каллисто.

Определение масс звезд и галактик

Для того чтобы найти характеристики одинарных звездных систем применяется гравиметрический метод. Его суть в измерении гравитационного красного смещения света звезды. Оно измеряется по формуле ∆V=0,635 M/R, где M и R – масса и радиус звезды, соответственно.

Косвенно можно также вычислить массу звезды по видимому спектру и светимости. Сначала определяется ее класс светимости по диаграмме Герцшпрунга-Рассела, а потом вычисляется зависимость масса/светимость. Такой способ не подходит для белых карликов и нейтронных звезд.

Масса галактик вычисляется в основном по скорости вращения ее звезд (или просто по относительной скорости звезд, если это не спиральная галактика). Все тот же всемирный закон тяготения Ньютона нам гласит, что центробежную силу звезд в галактике можно выразить в формуле:

Только в этот раз в формулу мы подставляем расстояние от Солнца до центра нашей галактики и его массу. Так можно рассчитать массу Млечного Пути, которая равняется 2,2 × 10⁴⁴г.

Не забываем, что эта цифра – это масса галактики без учета звезд, орбиты которых располагаются вне орбиты вращения Солнца. Поэтому для более точных расчетов берутся самые внешние звезды рукавов спиральных галактик.

Для эллиптических галактик способ нахождения массы схож, только там берется зависимость между угловым размером, скоростью движения звезд и общей массой.

Скорость, наверное, первая космическая, а не «вообще скорость»…

Ну дык просто. Первая космическая — когда ускорение свободного падения на нулевой высоте (т. е. на расстоянии от центра планеты, равном её разиусу) равно центростремительному. Ускорение свободного падения выражается через закон всемирного тяготения, а центрностремительное — через скорость и радиус. Вот приравняйте их друг другу — радиус как раз и найдётся.
Правда, понадобится ещё и масса планеты.