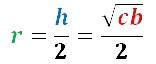Радиус вписанной окружности в трапецию, формула
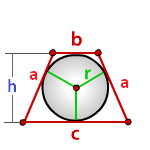
Радиус вписанной окружности в трапецию равен половине высоты трапеции.
[r=frac{h}{2}]
Радиус вписанной окружности в трапецию
Главное чтобы выполнялось условие при котором в данную трапецию возможно вписать окружность.
В четырехугольник окружность можно вписать только в том случае, если суммы его противоположных сторон равны. т.е.:
[ AB+DC = AD+BC]
или
[ 2a = b+c]
Иначе в данную трапецию нельзя вписать окружность.
бедро трапеции выражается через высоту по теореме Пифагора:
[ BC = a = sqrt{h^2 + Big(frac{c-b}{2}Big)^2} ]
Отсюда — зная все стороны трапеции вычислим такую высоту трапеции, которая удовлетворяет условию вписанной окружности (3).
[b+c = 2 sqrt{h^2 + Big(frac{c-b}{2}Big)^2}]
после небольших преобразований получим
[h = sqrt{ Big(frac{c+b}{2}Big)^2 — Big(frac{c-b}{2}Big)^2}]
[h = frac{1}{2} sqrt{ (c+b)^2 — (c-b)^2}]
используем формулы Квадрат суммы и Квадрат разности и после раскрытия скобок и упрощения получим
[h=sqrt{bc}]
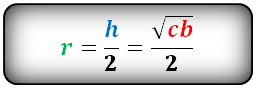
И соответственно радиус вписанной окружности в трапецию
[r=frac{h}{2}=frac{sqrt{bc}}{2}]
Вычислить, найти радиус вписанной окружности в трапецию по формуле (1,2,3,4,5)
Радиус вписанной окружности в трапецию |
стр. 259 |
|---|
Трапеция является несколько нестандартной фигурой среди четырехугольников. Она не является правильным многоугольником, однако обладает рядом отличительных свойств, среди которых – возможность вписать в равнобокую трапецию окружность. Это обусловлено тем, что для четырехугольников действует правило, согласно которому в него можно вписать окружность, если суммы его противоположных сторон равны. Не каждая трапеция соблюдает это правило, но если в нее все-таки вписана окружность, значит, сумма ее оснований равна сумме боковых сторон. Поскольку радиусы окружности, опущенные на основания трапеции, находятся по отношению к ним под прямым углом, следовательно, они совпадают с высотой трапеции, из чего можно вывести формулу радиуса окружности вписанной в трапецию через высоту:
Так как окружность можно вписать только в трапецию, у которой суммы противоположных сторон равны, то путем нехитрых преобразований через формулы квадрата разности и квадрата суммы можно получить, что высота трапеции равна среднему геометрическому ее оснований a и b.
Следовательно, не зная высоты, можно вычислить радиус окружности, вписанной в трапецию, через основания:
Существует и другой способ найти радиус вписанной в трапецию окружности. Для этого необходимо провести биссектрисы двух углов у боковой стороны. Точка их пересечения должна совпасть с центром вписанной окружности, а также образовать прямой угол. Соответственно, радиус в таком треугольнике станет высотой, которая, исходя из его свойств, равна среднему геометрическому проекций катетов на гипотенузу, то есть боковую сторону трапеции.
Радиус вписанной окружности в трапецию, формула
Радиус вписанной окружности в трапецию равен половине высоты трапеции.
Главное чтобы выполнялось условие при котором в данную трапецию возможно вписать окружность. В четырехугольник окружность можно вписать только в том случае, если суммы его противоположных сторон равны. т.е.:
Иначе в данную трапецию нельзя вписать окружность.
бедро трапеции выражается через высоту по теореме Пифагора:
Отсюда — зная все стороны трапеции вычислим такую высоту трапеции, которая удовлетворяет условию вписанной окружности (3).
после небольших преобразований получим
используем формулы Квадрат суммы и Квадрат разности и после раскрытия скобок и упрощения получим
И соответственно радиус вписанной окружности в трапецию
Трапеция. Формулы, признаки и свойства трапеции
Параллельные стороны называются основами трапеции, а две другие боковыми сторонами
Так же, трапецией называется четырехугольник, у которого одна пара противоположных сторон параллельна, и стороны не равны между собой.
- Основы трапеции — параллельные стороны
- Боковые стороны — две другие стороны
- Средняя линия — отрезок, соединяющий середины боковых сторон.
- Равнобедренная трапеция — трапеция, у которой боковые стороны равны
- Прямоугольная трапеция — трапеция, у которой одна из боковых сторон перпендикулярна основам
Основные свойства трапеции
AK = KB, AM = MC, BN = ND, CL = LD
3. Средняя линия трапеции параллельна основаниям и равна их полусумме:
BC : AD = OC : AO = OB : DO
d 1 2 + d 2 2 = 2 a b + c 2 + d 2
Сторона трапеции
Формулы определения длин сторон трапеции:
a = b + h · ( ctg α + ctg β )
b = a — h · ( ctg α + ctg β )
a = b + c· cos α + d· cos β
b = a — c· cos α — d· cos β
4. Формулы боковых сторон через высоту и углы при нижнем основании:
Средняя линия трапеции
Формулы определения длины средней линии трапеции:
1. Формула определения длины средней линии через длины оснований:
2. Формула определения длины средней линии через площадь и высоту:
Высота трапеции
Формулы определения длины высоты трапеции:
h = c· sin α = d· sin β
2. Формула высоты через диагонали и углы между ними:
| h = | sin γ · | d 1 d 2 | = | sin δ · | d 1 d 2 |
| a + b | a + b |
3. Формула высоты через диагонали, углы между ними и среднюю линию:
| h = | sin γ · | d 1 d 2 | = | sin δ · | d 1 d 2 |
| 2 m | 2 m |
4. Формула высоты трапеции через площадь и длины оснований:
5. Формула высоты трапеции через площадь и длину средней линии:
Диагонали трапеции
Формулы определения длины диагоналей трапеции:
d 1 = √ a 2 + d 2 — 2 ad· cos β
d 2 = √ a 2 + c 2 — 2 ac· cos β
2. Формулы диагоналей через четыре стороны:
| d 1 = | √ | d 2 + ab — | a ( d 2 — c 2 ) |
| a — b |
| d 2 = | √ | c 2 + ab — | a ( c 2 — d 2 ) |
| a — b |
d 1 = √ h 2 + ( a — h · ctg β ) 2 = √ h 2 + ( b + h · ctg α ) 2
d 2 = √ h 2 + ( a — h · ctg α ) 2 = √ h 2 + ( b + h · ctg β ) 2
d 1 = √ c 2 + d 2 + 2 ab — d 2 2
d 2 = √ c 2 + d 2 + 2 ab — d 1 2
Площадь трапеции
Формулы определения площади трапеции:
1. Формула площади через основания и высоту:
3. Формула площади через диагонали и угол между ними:
| S = | d 1 d 2 | · sin γ | = | d 1 d 2 | · sin δ |
| 2 | 2 |
4. Формула площади через четыре стороны:
| S = | a + b | √ | c 2 — | ( | ( a — b ) 2 + c 2 — d 2 | ) | 2 |
| 2 | 2( a — b ) |
5. Формула Герона для трапеции
| S = | a + b | √ ( p — a )( p — b )( p — a — c )( p — a — d ) |
| | a — b | |
где
| p = | a + b + c + d | — полупериметр трапеции. |
| 2 |
Периметр трапеции
Формула определения периметра трапеции:
1. Формула периметра через основания:
Окружность описанная вокруг трапеции
Формула определения радиуса описанной вокруг трапеции окружности:
1. Формула радиуса через стороны и диагональ:
| R = | a·c·d 1 |
| 4√ p ( p — a )( p — c )( p — d 1) |
где
a — большее основание
Окружность вписанная в трапецию
Формула определения радиуса вписанной в трапецию окружности
1. Формула радиуса вписанной окружности через высоту:
Другие отрезки разносторонней трапеции
Формулы определения длин отрезков проходящих через трапецию:
1. Формула определения длин отрезков проходящих через трапецию:
| KM = NL = | b | KN = ML = | a | TO = OQ = | a · b |
| 2 | 2 | a + b |
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
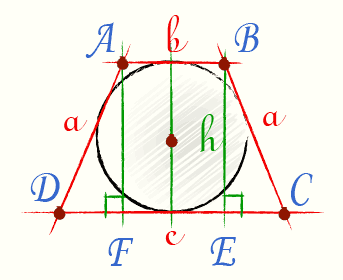
Радиус вписанной окружности в трапецию
с — нижнее основание
b — верхнее основание
a — боковые стороны
h — высота
Формула радиуса вписанной окружности равнобочной трапеции ( r ):
Калькулятор — вычислить, найти радиус вписанной окружности в равнобочную трапецию
http://ru.onlinemschool.com/math/formula/trapezium/
http://www-formula.ru/2011-09-22-03-33-33
Радиус вписанной окружности в трапецию
Радиус вписанной окружности
Трапецией является четырехугольник, имеющий 2 параллельные стороны. Они считаются основанием трапеции. Боковыми считаются остальные две не параллельные стороны. В трапецию несложно вписать окружность при условии равенства сумм противоположных ее сторон. Это значит, что сумма оснований трапеции равняется сумме боковых сторон. Если это условие не выполняется, окружность вписать нельзя. Вписанная окружность должна касаться всех ее сторон. В точке пересечения биссектрис трапеции находится центр вписанной окружности. Расчет радиуса производится следующим образом:
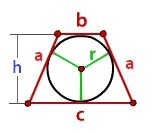
В представленной формуле:
b — величина верхнего основания;
с — нижнего;
a — величина боковых сторон;
h — длина высоты;
r — радиус.
Для определения радиуса вписанной трапеции, нужно высоту трапеции поделить на 2. Если известны величины оснований трапеции, то радиус равен половине корня квадратного из произведения его оснований.
С помощью онлайн калькулятора вы сможете быстро вычислить нужный радиус. Вам потребуется лишь подставить в формулу исходные величины.
Радиус вписанной окружности в трапецию
с — нижнее основание
b — верхнее основание
a — боковые стороны
h — высота
Формула радиуса вписанной окружности равнобочной трапеции (r):
Калькулятор — вычислить, найти радиус вписанной окружности в равнобочную трапецию
- Подробности
-
Автор: Administrator
-
Опубликовано: 09 сентября 2011
-
Обновлено: 13 августа 2021