Как найти радиус круга по клеткам - AvtoShod.ru - решение различных проблем

Задача № 1

На клетчатой бумаге с размером клетки 1 на 1 изображён прямоугольник (Рис. 1). Найдите радиус окружности, описанной около этого прямоугольника.

Решение

Чтобы найти радиус окружности, необходимо вспомнить правило, гласящее: «Радиус окружности, описанной около прямоугольника, равен половине его диагонали».

Найдем диагональ этого прямоугольника.

Из рисунка (Рис. 1) видно, что BD = 5

Диагональ равна 5, поэтому радиус равен 2,5.

Ответ: 2,5.

Задача № 2

На клетчатой бумаге с размером клетки √2 на √2 изображён квадрат (Рис. 2). Найдите радиус окружности, вписанной в этот квадрат.

Решение

Учтем, что по условию задачи размер клеток равен √2 на √2. Чтобы найти радиус окружности, необходимо вспомнить правило, гласящее: «Радиус окружности, вписанной в квадрат, равен половине его стороны». Найдем сторону квадрата:

Тогда радиус вписанной окружности равен:

Ответ: 2.

Задача № 3

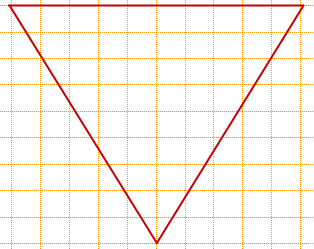
На клетчатой бумаге с размером клетки 1 на 1 изображён равносторонний треугольник (Рис. 3). Найдите радиус описанной около него окружности.

Решение

Чтобы найти радиус окружности, необходимо вспомнить правило, гласящее: «Радиус окружности, описанной вокруг равностороннего треугольника, равен двум третьим его высоты». Из рисунка (Рис. 3) видим, что высота равна «3». Поэтому радиус описанной окружности будет равен 3 х 2/3 = 2.

Ответ: 2.

Автор — Андрей Найденов

Больше уроков и заданий по всем школьным предметам в онлайн-школе «Альфа». Запишитесь на пробное занятие прямо сейчас!

Запишитесь на бесплатное тестирование знаний!

Источник

Задача 1

На клетчатой бумаге с размером клетки 1×1 изображён равносторонний треугольник. Найти радиус вписанной в него окружности.

Решение:

Поскольку формула радиуса вписанной в правильный треугольник окружности содержит иррациональность:

$[r = frac{a}{{2sqrt 3 }} = frac{{asqrt 3 }}{6},]$

использовать её на экзамене, где требуется точный ответ, а не его приближённое значение, нет смысла. Да и длина стороны треугольника задана в таких заданиях не целым числом.

Зато высота треугольника — целое число. По свойству равностороннего треугольника его высота равна сумме радиусов вписанной и описанной окружности:

причем

$[r = frac{1}{3}h,R = frac{2}{3}h.]$

Итак, чтобы найти радиус вписанной в равносторонний треугольник окружности, нужно посчитать по клеткам длину высоты и найти от неё треть.

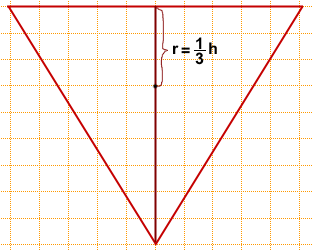
В данной задаче длина высоты равна 9 клеткам (h=9), следовательно,

$[r = frac{1}{3}h = frac{1}{3} cdot 9 = 3.]$

Ответ: 3.

Задача 2

На клетчатой бумаге с размером клетки 1×1 изображён равносторонний треугольник. Найти радиус описанной около него окружности.

Решение:

Находим по клеткам высоту данного треугольника:

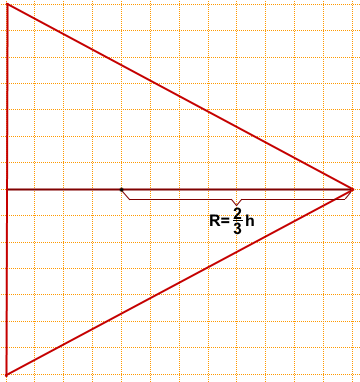
h=12.

Радиус описанной около равностороннего треугольника окружности составляет две третьих его высоты:

$[ R = frac{2}{3}h = frac{2}{3} cdot 12 ]$

Ответ: 8.

Источник

На клетчатой бумаге изображены два круга. Площадь внутреннего круга равна 1. Найдите площадь заштрихованной фигуры.

Задачи по геометрии в «клетках» встречаются и в ОГЭ и в ЕГЭ по математике, а также на ВПР.

Поэтому нужно уметь решать такие задачи по общему алгоритму.

1) Прежде всего нужно учесть размеры клетки. В данном случае он не указан, значит размеры не влияют на решение.

2) Затем нужно уметь считать размеры фигур, в данном случае радиусы кругов. Они равны соответственно 3 и 6 клеткам (условно), то есть радиус большого круга в 2 раза больше, чем радиус меньшего круга.

3) Далее ищем то, что требуется. В данной задаче нужно найти площадь заштрихованной фигуры. Её можно найти как разность площадей большого и малого кругов (оптимальный вариант). Остается найти площадь большого круга, она в 4 раза больше площади малого круга (так как площадь пропорциональна квадрату радиуса), то есть равна 4. 4-1 =3. Ответ площадь заштрихованной фигуры равна 3 (единицу измерения не указываем, да она и не дана по условию).

система выбрала этот ответ лучшим

Лёля Про
[20.9K]

5 лет назад

решение:

1) Мы видим по рисунку, что радиус внешнего круга равен 6 (см), а радиус внутреннего круга равен 3 (см).

2)Если радиус большего круга вдвое больше, чем радиус наименьшего круга, то площадь большего круга в четыре раза больше площади меньшего круга:

Sб = 4 * 1 = 4 (см^2)

3) Мы можем найти теперь площадь заштрихованной фигуры и она равна разности площадей кругов:

Sб — Sм

4 − 1 = 3 (см^2)

Ответ: площадь заштрихованной фигуры равна 3см^2

Поскольку рисунок выполнен на бумаге в клеточку, то у нас есть не только площадь меньшего круга, но и единица измерения радиуса круга — клеточка. Радиус маленького круга равен трем клеточкам, радиус большого — 6 клеточкам, мы просто считаем клеточки на рисунке. То есть радиус большого круга в два раза больше радиуса маленького.

Площадь круга находится по формуле ПиэР в квадрате: S=πR². Значит если радиус круга увеличится в два раза, то площадь круга увеличится в четыре раза. Следовательно большой круг по площади в четыре раза больше маленького, его площадь равна 4.

Но нам требуется найти площадь заштрихованной фигуры, а она равна площади большого круга за вычетом площади маленького. Получаем что площадь этой фигуры равна 4-1=3.

tana76
[124K]

5 лет назад

По рисунку видно, что радиус внешнего круга в два раза превышает радиус внутреннего круга: шесть клеточек — радиус внутреннего и 12 клеточек — радиус внешнего круга.

Этого вполне достаточно для дальнейших рассуждений.

Формула площади круга — «пи» х квадрат радиуса.

Значит, площадь внешнего круга, выраженная через радиус меньшего круга,такая:

«пи» х квадрат от числа (2 х r) (поскольку радиус в два раза больше), или больше в 4 раза.

Значит, площадь заштрихованной фигуры будет разницей между площадями кругов, или 4-1=3 кв.см..

bezdelnik
[34.1K]

5 лет назад

Площадь большого круга Sб = pi*R^2 = pi*144, площадь малого круга Sм = pi*36. Площадь заштрихованной фигуры Sф = Sб — Sм = pi*144 — pi*36 = pi(144- 36) = pi*108 = 339,292… квадратных единицы. Во всех ответах до меня решения не полные, в них найдено соотношение площадей, а не площадь заштрихованной фигуры.

Знаете ответ?

Источник

В этой статье речь пойдет о фигурах на квадратной решетке. В этом разделе присутствует несколько типов задач, это:

1) определение градусной меры угла;

2) определение тангенса угла (косинуса, синуса);

3) определение площади той или иной фигуры — трапеции, параллелограмма, сектора круга, треугольника и т.п.;

4) определение наибольшей (наименьшей) медианы (высоты) треугольника;

5) определение радиуса вписанной в треугольник (описанной около треугольника) окружности;

6) определение площади сложных или составных фигур.

Разберем задачи каждого типа.

Определение градусной меры угла.

1. Определите градусную меру угла:

Данный угол — тупой, и можно заметить, что левый луч, образующий его, является биссектрисой прямого угла (см. второй рисунок, угол показан рыжими прямыми). Тогда градусная мера этого угла равна:

Ответ: 135circ

2. Определите градусную меру угла (имеется в виду «рыжий» угол):

В этой задаче все просто, если вспомнить, что любой угол, вписанный в окружность и опирающийся на диаметр, равен 90circ

Ответ: 90circ

3. Определите градусную меру угла (рыжий).

Имеем правильный шестиугольник. Угол, градусную меру которого нам надо определить — вписанный.

Он опирается на дугу, которую стягивает хорда, являющаяся стороной шестиугольника. Тогда центральный угол, опирающийся на ту же дугу, это 1/6 часть всей окружности, или 60circ . Вписанный угол вдвое меньше центрального, если они опираются на одну и ту же дугу, значит, искомый угол равен 30circ .

4. Определите градусную меру угла.

«Нехорошая» задача. В данной задаче определить градусную меру угла можно только приближенно, однако мы не можем вписать приближенный ответ в бланк. Выделенный рыжим угол — тупой, можно заметить , что он состоит из прямого угла и еще некоторой части. Эту часть можно определить только «на глаз» — прикинуть, что она составляет примерно третью часть прямого угла, или 30circ . Тогда весь угол — . Ответ — 120circ . К сожалению такие задачи, где приходится прикидывать, встречаются.

Определение синусов, косинусов, тангенсов углов.

Здесь придется вспомнить геометрические определения синуса, косинуса, тангенса:

Синус угла — отношение противолежащего катета к гипотенузе.

Косинус угла — отношение прилежащего катета к гипотенузе.

Тангенс угла — отношение противолежащего катета к прилежащему.

5. Определить синус, косинус и тангенс угла.

Для того, чтобы воспользоваться определениями синуса, косинуса и тангенса, надо сначала выделить прямоугольный треугольник.

Конечно, удобнее вычислять, если катеты и гипотенуза этого треугольника будут целыми числами. Катеты, понятно, лежат на прямых, образующих саму решетку, поэтому нужно смотреть на луч этого угла, который станет гипотенузой нашего треугольника, и найти такое место, где этот луч пересечет узел решетки:

Тогда в нашем треугольнике катеты — 3 и 4 клетки, а гипотенузу найдем по теореме Пифагора.

Тогда: синус угла — 4/5, или 0,8, косинус угла — 3/5, или 0,6, тангенс угла — 4/3, или 1,33 — кстати, вы подумали, как записать такое число в бланк ответов?

6. Определить тангенс угла:

Вспомним, что тангенс тупого угла равен тангенсу острого, смежного с ним, взятого с отрицательным знаком.

Надо найти тангенс смежного острого угла. Так как луч, образующий его — гипотенуза прямого угла и проходит прямо по узлам решетки, то катеты треугольников, образуемых этим лучом, всегда равны. Тогда тангенс равен:. Искомый тангенс тупого угла — (-1).

Ответ: -1

7. Определить тангенс угла.

Данный угол — острый, его тангенс — положительный. Осталось найти подходящий узел решетки, чтобы построить прямоугольный треугольник (для этого черным помечена опорная точка — узел решетки). В этом треугольнике считаем количество клеточек в каждом из катетов и определяем тангенс. У нас катеты — 1 и 4 клеточки, искомый тангенс — 1/4 .

8. Определить тангенс угла.

Данный угол — тупой, значит, его тангенс — отрицателен. Определяем тангенс смежного с ним острого угла, ставим перед ним минус — и дело в шляпе. Чтобы определить тангенс острого угла, выбираем целый узел, через который проходит луч, образующий угол — помечен черной точкой. Катеты получившегося треугольника — 1 и 3 клетки, тангенс равен отношению противолежащего катета к прилежащему, значит, 3/1=3 . Искомый тангенс тупого угла — (-3).

Ответ: -3

9 и 10. Попробуйте сами определить тангенсы углов на рисунках ниже. Ответ — в конце статьи.

Определение площади той или иной фигуры.

11. Определите площадь трапеции:

Несмотря на то, что трапецию уложили на бок, сразу можем определить, где у нее основания — ведь, чтобы определить площадь трапеции, нужно знать основания и высоту трапеции:

$S_TR={{a+b}/2}h$

У нас верхнее (малое) основание — 2 клетки, нижнее (большое) — 4 клетки. Высота трапеции — 2 клетки. Тогда вычисляем площадь: $S_TR={{2+4}/2}2=6$

Ответ: 6

12. Определите площадь параллелограмма:

Для вычисления площади параллелограмма достаточно высоты и основания (есть, конечно, и другие формулы, но в данном случае, на решетке, они вряд ли пригодятся): . У данного параллелограмма основание равно 1 клетке, а вот высота? Высота — всегда перпендикуляр к основанию… или к его продолжению! Вы согласны, что высота этого параллелограмма равна 4 клеткам? Тогда его площадь .

Ответ:4.

13. Определите площадь ромба.

Нетрудно понять, что посчитать площадь ромба удобно, разделив его на треугольники либо по вертикали, либо по горизонтали. Имеем два треугольника с основанием 6 клеток, высотой 2 клетки (поделила по горизонтали). Площадь треугольника определяем по формуле: $S_Delta={a*h}/2=6$ .

Площадь ромба равна .

Кстати, площадь ромба здесь еще очень удобно определить как половину произведения его диагоналей: $2S_Delta={d_1*d_2}/2={6*4}/2=12$ .

14. Определите площадь кругового сектора, в ответ запишите площадь, деленную на .

Радиус окружности равен 3, поэтому площадь всего круга будет: $S_kr={pi}r^2=9{pi}$ .

Так как центральный угол сектора равен 120circ , а это 1/3 от 360circ , то площадь сектора будет равна 1/3 от площади всего круга, то есть $S={1/3}S_kr=3{pi}$ . Делим на число и записываем ответ: 3

15. Определите площадь треугольника:

Чтобы найти площадь треугольника, нужно знать его основание и высоту. За основание может быть принята любая удобная сторона, удобная — значит, она расположена строго вертикально или горизонтально — так, чтобы ее длину в клеточках было удобно считать. Здесь возьмем за основание самую длинную сторону, расположенную вертикально, ее длина в клеточках — 10. Проведем к этой стороне высоту из правой вершины, высота получится равной 3 клеточкам. Тогда площадь этого треугольника: $S_Delta={a*h}/2={10*3}/2=15$ .

Ответ:15.

16. Определите площадь треугольника:

Основание его равно 2 клеткам, высота — 4 клеточки, и неважно, что она не «попала» в основание, ведь она может быть опущена и на его продолжение. Тогда площадь равна: $S_Delta={a*h}/2={2*4}/2=4$ .

Ответ: 4.

Определение наибольшей или наименьшей высоты (или медианы) треугольника.

17. Определите наименьшую высоту треугольника. Размер клетки 1 см. Ответ дайте в см.

Проведем высоты из вершин данного треугольника к основаниям или их продолжениям:

Понятно, что самая маленькая высота — та, что внутри треугольника (а). Ее длина — 1 клеточка.

Ответ: 1

18. Найдите наибольшую медиану треугольника, изображенного на клетчатой бумаге с размером клетки 1 см. Ответ дайте в см.

В этом треугольнике нетрудно определить середины сторон — точки, в которых медианы пересекутся со сторонами треугольника (отмечены черными кружочками). Но медианы получаются близкими по длине — как узнать, какая все же длиннее?

Очевидно, что борьба развернется между медианами «b» и «c», «а» — не конкурент, она явно короче. Длину «с» можно определить сразу — это 5 клеточек. Осталось разобраться с медианой «b», и здесь нельзя выполнить расчет неточно. Воспользуемся тем, что треугольник изображен на сетке — тогда можно использовать теорему Пифагора. Построим прямоугольный треугольник на гипотенузе «b»:

Видно, что катеты этого треугольника 3 и 4 клетки, тогда гипотенуза (это и есть наша медиана «b») равна 5 и равна медиане «с». В ответ нужно записать длину наибольшей медианы, ответ: 5

19. Найдите наименьшую медиану треугольника, изображенного на клетчатой бумаге с размером клетки 1 см. Ответ дайте в см.

Проведем медианы. Самую длинную медиану (к самой короткой стороне треугольника) не проводим.

Какая из медиан короче — рыжая или зеленая? Если заметить, что два этих отрезка являются перпендикуляром и наклонной между двумя параллельными прямыми, образующими саму сетку, то очевидно, что перпендикуляр — рыжая медиана — короче (по теореме). Ее длина — 2 клетки, записываем ответ: 2.

20. Найдите наибольшую высоту треугольника, изображенного на клетчатой бумаге с размером клетки 1 см. Ответ дайте в см.

Очевидно, что здесь наибольшая высота — это высота, проведенная к продолжению наименьшей стороны треугольника, ее длина составит 4 клетки. Ответ: 4.

Определение радиуса вписанной в треугольник (описанной около треугольника) окружности.

21. Для данного треугольника определите радиус описанной около него окружности. Размер клетки — 1 см. Ответ дайте в см.

В такого типа задачах может помочь знание формул. Нужно помнить, что

$S_Delta={a*b*c}/{4R}$ , где a, b и c — стороны треугольника, R — радиус описанной окружности.

, где — полупериметр треугольника, r — радиус вписанной окружности.

Площадь этого треугольника — $S_Delta={a*h}/2={8*2}/2=8$ . Длины его сторон: основание — 8, боковые — по теореме Пифагора — $l=sqrt{4^2+2^2}=sqrt{20}$

Считаем радиус описанной окружности: $R={a*b*c}/{4S_Delta}={(sqrt{20})^2*8}/{4*8}=5$

Ответ: 5

22. Определить радиус вписанной в треугольник окружности. Размер клетки 1 см.

Снова понадобятся стороны — чтобы определить полупериметр. Катеты: 5 и 12, тогда гипотенуза — 13 (пифагорова тройка).

Полупериметр:

Это прямоугольный треугольник, площадь найдем через катеты: $S_Delta={a*b}/2={5*12}/2=30$

Тогда радиус вписанной окружности:

Ответ:2

23. Определим радиус описанной около треугольника окружности:

Самая длинная — 10, самая короткая — $l=sqrt{1^2+3^2}=sqrt{10}$ .Его площадь мы нашли в задаче 15, она равна 15 квадратным см. Осталось найти стороны.

Средняя: $l=sqrt{9^2+3^2}=sqrt{90}$ .

Считаем радиус описанной окружности: $R={a*b*c}/{4S_Delta}={(sqrt{10})*(sqrt{90})*10}/{4*15}=300/60=5$

Ответ:5

Определение площади сложных или составных фигур.

При определении площадей сложных фигур часто их можно разбить на более простые, определить их площади и затем сложить. Но в ряде случаев можно пользоваться и формулой Пика. Она подходит для фигур, нарисованных на клетчатой бумаге, и невырожденых -площадь фигуры ненулевая, все вершины имеют целые координаты, а стороны не пересекают друг друга.

Здесь V — число целочисленных точек внутри фигуры (целочисленные точки — это узлы нашей решетки), G — число целочисленных точек на границе фигуры (на линиях, ограничивающих фигуру). Применять формулу для фигур, содержащих элементы круга не стоит — речь идет о фигурах, полученных при пересечении прямых.

Однако сначала разберем простые случаи.

24. Определите площадь изображенной на клетчатой бумаге фигуры. Размер клетки 1 см. Ответ дайте в кв. см.

Видно, что фигура состоит из двух треугольников, причем площадь маленького нужно вычесть из площади большого. Определяем площади, большой треугольник: $S_Delta={a*h}/2={4*3}/2=6$ . Малый треугольник: . Вычитаем из большей площади меньшую: 4. Ответ: 4.

Попробуем воспользоваться формулой Пика: . Внутри фигуры три узла решетки, на границе — 4. Тогда площадь: — как видите, ответ тот же.

25. Определите площадь квадрата, размер клетки 1 см. Ответ дайте в кв. см.

Очень хочется повернуть квадрат так, чтобы стоял на стороне, и сказать, что сторона равна 3, а площадь — 9. Но это не так. Определим длину стороны квадрата по теореме Пифагора: $a=sqrt{3^2+1^2}=sqrt{10}$ . Тогда площадь этого квадрата равна 10. Ответ: 10.

Получится ли такой же ответ по нашей волшебной формуле? Внутри фигуры девять узлов решетки, на границе — 4 (вершины квадрата). Тогда площадь: .

26. Определите площадь заштрихованной фигуры, размер клетки 1 см. Ответ дайте в кв. см.

При отыскании площади такой фигуры принцип тот же: находим площадь большого квадрата и вычитаем площадь малого.

Сторона большого квадрата: $a=sqrt{3^2+3^2}=sqrt{18}$ , значит, его площадь — 18 кв. см.

Сторона малого: $a=sqrt{2^2+2^2}=sqrt{8}$ , его площадь 8 кв. см.

Разность площадей составляет 10 кв. см — это и есть искомая площадь.

По формуле Пика площадь этой фигуры определить нельзя: верный ответ не получится, так как, строго говоря, здесь не одна фигура, а две.

27. Определите площадь кольца. Размер клетки 1 см. В ответ запишите площадь в кв. см, деленную на .

Здесь легко по клеткам определить радиус как большего, так и меньшего круга, посчитать их площади и затем вычесть одно из другого.

Больший круг: $S=pi{r^2}=4pi$

Меньший круг: $s=pi{r^2}=pi$

Разность составляет: . В ответ записываем найденную площадь, деленную на число : 3

28. Определить площадь изображенной на клетчатой бумаге фигуры. Размер клетки 1 см. Ответ дайте в кв. см.

Эту фигуру можно разбить на три треугольника и определить сумму их площадей: 3+1+1=5.

По формуле Пика имеем то же самое: . Внутри фигуры два узла решетки, на границе — 8. Тогда площадь: — ответ тот же.

29. Определить площадь изображенной на клетчатой бумаге фигуры. Размер клетки 1 см. Ответ дайте в кв. см.

В этом случае надо еще придумать, как разбить нашу фигуру на более простые. Нужно сделать это так, чтобы площади определялись точно, без «ну, там примерно полклеточки». И это не обязательно должны быть треугольники!

Это могут быть трапеция и треугольник, а площадь трапеции мы уже научились находить. Но в этом случае точно определить площадь можно только разбив фигуру на треугольники: у меня вышло 4 кв. см.

По формуле Пика: внутри два узла решетки, на границе — 6. Тогда площадь: . Ответ: 4

30. Самостоятельно определите площадь фигуры удобным вам способом:

Ответ — в конце статьи.

31. Вот такая интересная фигура встретилась на пробном ЕГЭ в 2014 году одному из учеников:

Как тут быть? Можно вычленить полный круг и определить его площадь, но остается еще «рыбий хвост» — этакий сдавленный ромб, и как определить его площадь?

Этот «хвост» — круг, из которого вырезали 8 сегментов — см. рисунок, а площадь сегмента — это площадь сектора (в нашем случае — четверть круга) минус площадь треугольника (красными линиями). Считаем: «тело» рыбы — полный круг. Радиус его 2 клетки, площадь тогда 4pi . Площадь сектора — , площадь треугольника — 2. Площадь сегмента равна: pi-2 , а восьми сегментов — 8pi-16 . Площадь «хвоста»:

. Соединим «хвост» и «тело»: .

Ответ: 16

Ответ на 9 задачу: 1,5

Ответ на 10 задачу: 1/2

Ответ на 30 задачу: 5

Если что-то все же осталось непонятно, задавайте ваши вопросы в комментариях, я обязательно отвечу!

Источник

Клеточки на бумаге позволяют многие построения проводить только с
помощью линейки, причём на этой линейке может даже не быть делений. Но всегда
нужно помнить свойства геометрических фигур, ведь именно они позволяют
использовать клеточки в полной мере.

Давайте разделим отрезок пополам. Для этого начертим прямоугольник так, чтобы данный
отрезок был его диагональю. Мы знаем, что диагонали прямоугольника при
пересечении делятся пополам. Тогда проведём в нашем прямоугольнике вторую
диагональ и таким образом разделим отрезок на два равных отрезка.

Много интересного можно получить из экспериментов с прямоугольным
треугольником на клетчатой бумаге.

Изобразим произвольный прямоугольный треугольник. А затем повернём
его на , например, против часовой стрелки.

Измерим угол между большими сторонами (гипотенузами) получившихся
треугольников. Для этого воспользуемся транспортиром. Приложим его таким
образом, чтобы точка пересечения сторон совместилась с серединой основания
транспортира, а одна из сторон прошла через начало отсчёта на шкале
транспортира. Теперь находим штрих на шкале, через который проходит другая
сторона. Помним, что мы используем ту шкалу, на которой располагается .

Видим, что этому штриху соответствует , а значит, угол между большими сторонами треугольников прямой.

Таким образом, поворачивая треугольник на , мы тем самым поворачиваем все его элементы, в том числе и
стороны, на тот же угол, значит, угол между большими сторонами также равен .

Используя результат этого опыта, выполним задание. Постройте
перпендикуляр к отрезку, соединившему два любых узла клетчатой бумаги.

Решение. Проведём отрезок, который
соединяет два произвольных узла бумаги в клетку. Затем достроим отрезок до
прямоугольного треугольника так, чтобы данный отрезок являлся гипотенузой, то
есть большей стороной, а затем повернём треугольник на вокруг произвольной точки.

Получается, что гипотенуза получившегося треугольника является
перпендикуляром к заданному отрезку.

Иногда бывают случаи, когда надо нарисовать окружность, а циркуля
нет, но есть бумага в клетку.

На одном из предыдущих занятий мы с вами познакомились с правилом
(, , ), которое позволяет изобразить окружность на клетчатой бумаге от
руки. Правда, речь шла об окружности, радиус которой равен 5 клеткам.

Сейчас мы выведем правило, с помощью которого от руки можно
изобразить окружность, радиус которой равен 13 клеткам.

Для удобства с помощью циркуля начертим окружность с радиусом 13
клеток с центром в узле клеток.

Итак, возьмём узел клетчатой бумаги на данной окружности. Отступив
на 1 клетку вправо и на 5 клеток вверх, поставим вторую точку. Отступая от
второй точки вправо на 1 клетку и вверх на 2 клетки, ставим третью точку.
Далее, отступив 4 клетки вправо и 4 клетки вверх, находим четвёртую точку.
Отступив 2 клетки вправо и 1 клетку вверх, поставим 5 точку. Шестая точка
находится на расстоянии 5 клеток вправо и 1 клетки вверх от пятой точки.

Если соединить эти шесть точек плавной линией, получим четверть
окружности.

Чтобы достроить окружность нам надо повторить эти действия ещё три
раза, изменяя направление движения.

Правило, с помощью которого можно построить окружность с радиусом,
равным 13и клеткам, можно записать следующим образом: , , , , .

Вернёмся к выполнению заданий. Найдите площадь
прямоугольного треугольника (с катетами клетки и клетки), если все его вершины лежат в узлах клеток, а две стороны
проходят по сторонам клеток. Площадь одной клетки примем за единицу.

Решение. Изобразим прямоугольный треугольник
так, чтобы все его вершины лежали в узлах клеток, а две стороны проходили по
сторонам клеток.

Затем достроим этот треугольник до прямоугольника так, чтобы
вершины нашего треугольника совпали с вершинами прямоугольника, а стороны,
которые являются катетами нашего треугольника, лежали на сторонах
прямоугольника. Затем сосчитаем количество клеточек в прямоугольнике. Их 12. То
есть площадь прямоугольника равна 12 (ед. кв.).

Заметим, что построенный прямоугольник состоит из двух равных прямоугольных
треугольников. Тогда площадь нашего треугольника равна половине площади
прямоугольника. А это (ед. кв.).

Следующее задание. Начертите два разных прямоугольных
треугольника, площади которых равны 2 клеткам.

Решение. Давайте изобразим два
прямоугольника, площади которых равны 4 клеткам.

Это прямоугольник со сторонами, равными 1 клетке и 4 клеткам. И
квадрат со стороной, равной 2 клеткам.

Теперь в прямоугольнике проведём диагональ, которая разделит его
на два равных прямоугольных треугольника. Площадь каждого из них будет равна (кл.).

Проведём диагональ в квадрате. Она разделит его на два равных
прямоугольных треугольника. Площадь каждого из них будет равна (кл.).

Так, мы получили два различных прямоугольных треугольника, площадь
каждого из которых равна двум клеткам.

Эта задача показывает, что для равенства фигур ещё недостаточно
равенства их площадей.

Сейчас мы с вами познакомимся с формулой Пика, которая
названа именем математика Георга Пика. В 16 лет он окончил школу и поступил в
Венский университет. В возрасте 17 лет была опубликована его первая работа.
Круг его математических интересов был очень широк. 67 его работ посвящены
многим разделам математики.

Широкую известность получила открытая им в 1899 году теорема Пика
для расчёта площади многоугольника.

C помощью формулы
Пика можно вычислить площадь произвольного многоугольника с вершинами в узлах
клетки. Формула имеет вид:

Здесь – число узлов внутри многоугольника, – число узлов на границе многоугольника, включая вершины.

Найдём площадь изображённого многоугольника. Для этого сосчитаем
число узлов внутри многоугольника. Оно равно 10. Теперь сосчитаем число узлов
на границе, включая вершины. Оно равно 7.

Подставим полученные значения в формулу: (ед. кв.).

Получили, что площадь данного многоугольника равна (ед. кв.).

Выполним задание. Найдите площадь многоугольника,
изображённого на рисунке.

Решение.

Источник

Не пропустите также: