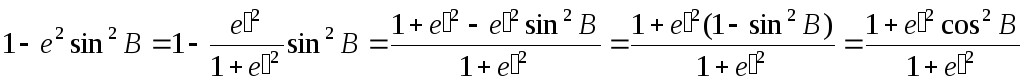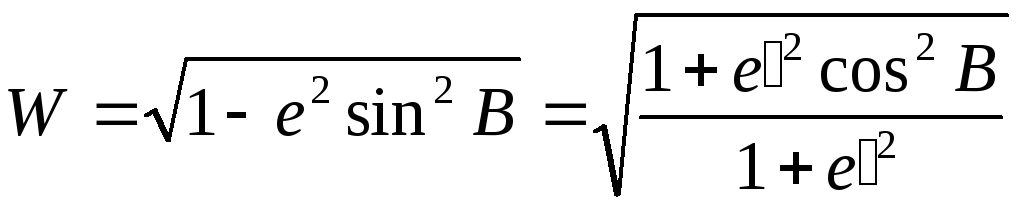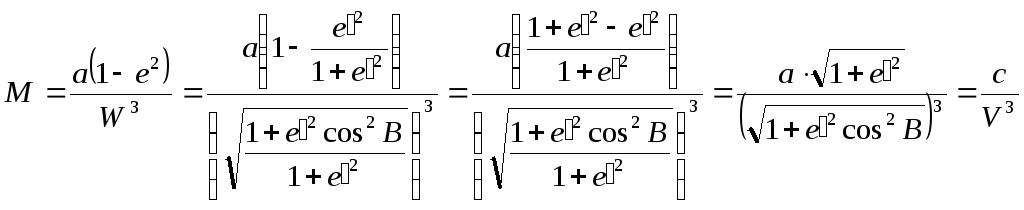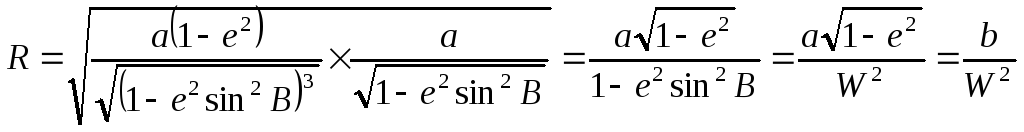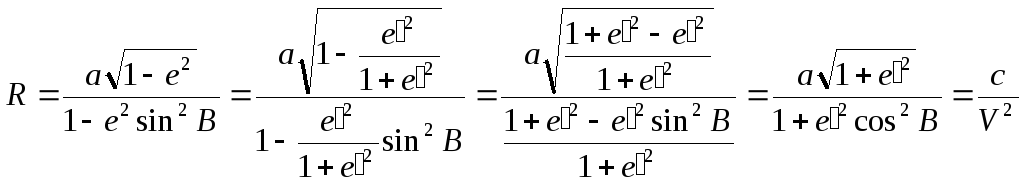From Wikipedia, the free encyclopedia
This article is about the general mathematical concept. For its optical applications, see Radius of curvature (optics).
In differential geometry, the radius of curvature (Rc), R, is the reciprocal of the curvature. For a curve, it equals the radius of the circular arc which best approximates the curve at that point. For surfaces, the radius of curvature is the radius of a circle that best fits a normal section or combinations thereof.[1][2][3]
Definition[edit]
In the case of a space curve, the radius of curvature is the length of the curvature vector.
In the case of a plane curve, then R is the absolute value of[3]
where s is the arc length from a fixed point on the curve, φ is the tangential angle and κ is the curvature.
Formula[edit]
In 2D[edit]
If the curve is given in Cartesian coordinates as y(x), i.e., as the graph of a function, then the radius of curvature is (assuming the curve is differentiable up to order 2):
and |z| denotes the absolute value of z.
Also in Classical mechanics branch of Physics Radius of curvature is given by (Net Velocity)²/Acceleration Perpendicular
If the curve is given parametrically by functions x(t) and y(t), then the radius of curvature is
Heuristically, this result can be interpreted as[2]
In n dimensions[edit]
If γ : ℝ → ℝn is a parametrized curve in ℝn then the radius of curvature at each point of the curve, ρ : ℝ → ℝ, is given by[3]
.
As a special case, if f(t) is a function from ℝ to ℝ, then the radius of curvature of its graph, γ(t) = (t, f(t)), is
Derivation[edit]
Let γ be as above, and fix t. We want to find the radius ρ of a parametrized circle which matches γ in its zeroth, first, and second derivatives at t. Clearly the radius will not depend on the position γ(t), only on the velocity γ′(t) and acceleration γ″(t). There are only three independent scalars that can be obtained from two vectors v and w, namely v · v, v · w, and w · w. Thus the radius of curvature must be a function of the three scalars |γ′(t)|2, |γ″(t)|2 and γ′(t) · γ″(t).[3]
The general equation for a parametrized circle in ℝn is
where c ∈ ℝn is the center of the circle (irrelevant since it disappears in the derivatives), a,b ∈ ℝn are perpendicular vectors of length ρ (that is, a · a = b · b = ρ2 and a · b = 0), and h : ℝ → ℝ is an arbitrary function which is twice differentiable at t.
The relevant derivatives of g work out to be
If we now equate these derivatives of g to the corresponding derivatives of γ at t we obtain
These three equations in three unknowns (ρ, h′(t) and h″(t)) can be solved for ρ, giving the formula for the radius of curvature:
or, omitting the parameter t for readability,
Examples[edit]
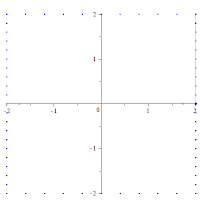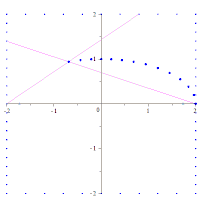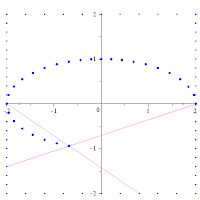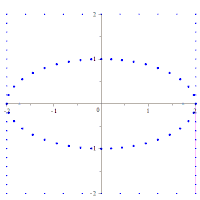
Semicircles and circles[edit]
For a semi-circle of radius a in the upper half-plane
An ellipse (red) and its evolute (blue). The dots are the vertices of the ellipse, at the points of greatest and least curvature.
For a semi-circle of radius a in the lower half-plane
The circle of radius a has a radius of curvature equal to a.
Ellipses[edit]
In an ellipse with major axis 2a and minor axis 2b, the vertices on the major axis have the smallest radius of curvature of any points, R = b2/a; and the vertices on the minor axis have the largest radius of curvature of any points, R = a2/b.
The ellipse’s radius of curvature, as a function of parameter t
[4]
And as a function of θ
Where e is the eccentricity of the ellipse and is given by:

Applications[edit]
- For the use in differential geometry, see Cesàro equation.
- For the radius of curvature of the earth (approximated by an oblate ellipsoid); see also: arc measurement
- Radius of curvature is also used in a three part equation for bending of beams.
- Radius of curvature (optics)
- Thin films technologies
- Printed electronics
- Minimum railway curve radius
- AFM probe
Stress in semiconductor structures[edit]
Stress in the semiconductor structure involving evaporated thin films usually results from the thermal expansion (thermal stress) during the manufacturing process. Thermal stress occurs because film depositions are usually made above room temperature. Upon cooling from the deposition temperature to room temperature, the difference in the thermal expansion coefficients of the substrate and the film cause thermal stress.[5]
Intrinsic stress results from the microstructure created in the film as atoms are deposited on the substrate. Tensile stress results from microvoids (small holes, considered to be defects) in the thin film, because of the attractive interaction of atoms across the voids.
The stress in thin film semiconductor structures results in the buckling of the wafers. The radius of the curvature of the stressed structure is related to stress tensor in the structure, and can be described by modified Stoney formula.[6] The topography of the stressed structure including radii of curvature can be measured using optical scanner methods. The modern scanner tools have capability to measure full topography of the substrate and to measure both principal radii of curvature, while providing the accuracy of the order of 0.1% for radii of curvature of 90 meters and more.[7]
See also[edit]
- Base curve radius
- Bend radius
- Degree of curvature (civil engineering)
- Osculating circle
- Track transition curve
References[edit]
- ^ Weisstien, Eric. «Radius of Curvature». Wolfram Mathworld. Retrieved 15 August 2016.
- ^ a b Kishan, Hari (2007). Differential Calculus. Atlantic Publishers & Dist. ISBN 9788126908202.
- ^ a b c d Love, Clyde E.; Rainville, Earl D. (1962). Differential and Integral Calculus (Sixth ed.). New York: MacMillan.
- ^ Weisstein, Eric W. «Ellipse». mathworld.wolfram.com. Retrieved 2022-02-23.
- ^ «Controlling Stress in Thin Films». Flipchips.com. Retrieved 2016-04-22.
- ^ «On the determination of film stress from substrate bending : Stoney’s formula and its limits» (PDF). Qucosa.de. Retrieved 2016-04-22.
- ^ Peter Walecki. «Model X». Zebraoptical.com. Retrieved 2016-04-22.
Further reading[edit]
- do Carmo, Manfredo (1976). Differential Geometry of Curves and Surfaces. ISBN 0-13-212589-7.
External links[edit]
- The Geometry Center: Principal Curvatures
- 15.3 Curvature and Radius of Curvature
- Weisstein, Eric W. «Principal Curvatures». MathWorld.
- Weisstein, Eric W. «Principal Radius of Curvature». MathWorld.
Российская кривая: коническое сечение 


В математике, эллипс — это плоская кривая , окружающая два фокальные точки, так что для всех точек на кривой сумму двух расстояний до фокальных точек является постоянной. Таким образом, он обобщает круг , который представляет собой особый тип эллипса, в котором две точки фокусировки совпадают. Удлинение эллипса измеряется его эксцентриситетом e, числом от e = 0 (предельный случай окружности) до e = 1 (предельный случай бесконечного удлинения, больше не эллипс, а парабола ).
Эллипс имеет простое алгебраическое решение для своей площади, но только приближения для его периметра, для которого требуется интегрирование для получения точного решения.
Анали уравнение стандартного эллипса с центром в начале координат с шириной 2a и высотой 2b имеет вид:
- x 2 a 2 + y 2 b 2 = 1. { displaystyle { frac {x ^ {2 }} {a ^ {2}}} + { frac {y ^ {2}} {b ^ {2}}} = 1.}
Предполагая, что a ≥ b, фокусы равны (± c, 0) для c = a 2 — b 2 { displaystyle c = { sqrt {a ^ {2} -b ^ {2}}}}
- (x, y) = (a cos (t), b sin (t)) для 0 ≤ t ≤ 2 π. { displaystyle (x, y) = (a cos (t), b sin (t)) quad { text {for}} quad 0 leq t leq 2 pi.}
эллипсы являются закрытым типом конического сечения : плоская кривая, отслеживающая пересечение конуса с плоскостью (см. рисунок). Эллипсы имеют много общего с двумя другими формами конических сечений, параболами и гиперболами, обе из которых являются открытыми и неограниченными. Угловое поперечное сечение цилиндра также является эллипсом.
Эллипс также может быть определен в терминах одной точки фокусировки и линии за пределами эллипса, называемой направляющей : для всех точек на эллипсе отношение расстояния к фокус, расстояние до директрисы является постоянным. Это постоянное соотношение является упомянутым выше эксцентриситетом:
- e = ca = 1 — b 2 a 2 { displaystyle e = { frac {c} {a}} = { sqrt {1 — { frac {b ^ { 2}} {a ^ {2}}}}}}
.
Эллипсы распространены в физике, астрономии и инженерии. Например, орбита каждой планеты в солнечной системе представляет собой эллипс с Солнцем в одной точке фокусировки (точнее, фокус — это барицентр пары Солнце — планета). То же верно и для спутников, вращающихся вокруг планет, и для всех других систем двух астрономических тел. Формы планет и звезд часто хорошо описываются эллипсоидами. Круг, если смотреть под боковым углом, как эллипс: то есть эллипс — это изображение круга под параллельной или перспективной проекцией. Эллипс также является самой простой фигурой Лиссажу, образованной, когда горизонтальные и вертикальные движения синусоиды с одинаковой точностью: аналогичный эффект приводит к эллиптической поляризации света в оптика.
Имя λλειψις (élleipsis, «упущение») было дано Аполлонием Пергским в его Кониксах.
Содержание
- 1 Определение как геометрическое место точек
- 2 В декартовых координатах
- 2.1 Стандартное уравнение
- 2.2 Параметры
- 2.2.1 Главные оси
- 2.2.2 Линейный эксцентриситет
- 2.2.3 Эксцентриситет
- 2.2.4 Semi-latus rectum
- 2.3 Касательная
- 2.4 Сдвинутый эллипс
- 2.5 Общий эллипс
- 3 Параметрическое представление
- 3.1 Стандартное параметрическое представление
- 3.2 Рациональное представление
- 3.3 Наклон касательной как параметр
- 3.4 Общий эллипс
- 4 Полярные формы
- 4.1 Полярная форма относительно центра
- 4.2 Полярная форма относительно фокуса
- 5 Эксцентриситет и свойство директрисы
- 6 Свойство отражения от фокуса к фокусу
- 7 Сопряженные диаметры
- 7.1 Теорема Аполлония о сопряженных диаметрах
- 8 Ортогональные касательные
- 9 Рисование эллипсов
- 9.1 Построение точки де Ла Хира
- 9.2 Штифты Метод струн
- 9.3 Методы бумажной ленты
- 9.4 Аппроксимац ия соприкаса с кругами
- 9.5 Поколение Штейнера
- 9.6 Как гипотрохоида
- 10 вписанные углы и трехточечная форма
- 10.1 окружности
- 10.1.1 теорема вписанных углов для окружностей
- 10.1.2 трехточечная форма уравнения окружности
- 10.2 эллипсы
- 10.2.1 вписанные Теорема об углах для эллипсов
- 10.2.2 Трехточечная форма уравнения эллипса
- 10.1 окружности
- 11 Соотношение полюсов и полюсов
- 12 Метрические свойства
- 12.1 Площадь
- 12.2 Окружность
- 12.3 Кривизна
- 13 В геометрии треугольника
- 14 В виде плоских сечений квадрик
- 15 Приложения
- 15.1 Физика
- 15.1.1 Эллиптические отражатели и акустика
- 15.1.2 Планетарные орбиты
- 15.1.3 Гармонические осцилляторы
- 15.1.4 Просмотр фаз
- 15.1.5 Эллиптические шестерни
- 15.1.6 Оптика
- 15.2 Статистика и финансы
- 15.3 Компьютерная графика
- 15.4 Теория оптимизации
- 15.1 Физика
- 16 См. Также
- 17 Примечания
- 18 Ссылки
- 19 Внешние ссылки
Определение как геометрическое место точек
эллипс может быть определен геометрически как набор или геометрическое место точек на евклидовой плоскости:
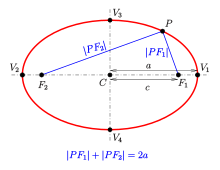
- Даны две фиксированные точки F 1, F 2 { displaystyle F_ {1}, F_ {2}}
называется фокусами и расстояние 2 a { displaystyle 2a}
, больше, чем расстояние между фокусами, эллипс — это набор точек P { displaystyle P}
такие, что сумма расстояний | P F 1 |, | P F 2 | { displaystyle | PF_ {1} |, | PF_ {2} |}
равно 2 a { displaystyle 2a}
:E = {P ∈ R 2 ∣ | P F 2 | + | P F 1 | = 2 а}. { Displaystyle E = {P in mathbb {R} ^ {2} , mid , | PF_ {2} | + | PF_ {1} | = 2a } .}
Средняя точка C { displaystyle C}




Случай F 1 = F 2 { displaystyle F_ {1} = F_ {2}}
Уравнение | P F 2 | + | P F 1 | Знак равно 2 а { Displaystyle | PF_ {2} | + | PF_ {1} | = 2a}
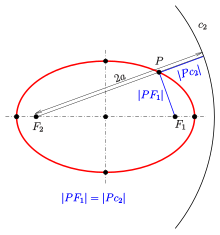
- If c 2 { displaystyle c_ {2}}
— круг со средней точкой F 2 { displaystyle F_ {2}}
и радиусом 2 a { displaystyle 2a}
, тогда расстояние от точки P { displaystyle P}
до окружности c 2 { displaystyle c_ {2}}
равно расстояние до фокуса F 1 { displaystyle F_ {1}}
:
- | P F 1 | = | P c 2 |. { displaystyle | PF_ {1} | = | Pc_ {2} |.}
- | P F 1 | = | P c 2 |. { displaystyle | PF_ {1} | = | Pc_ {2} |.}
c 2 { displaystyle c_ {2}}

Используя сферы Данделина, можно доказать, что любое плоское сечение конуса с плоскостью является эллипсом, при условии, что плоскость не содержит вершины и имеет наклон меньше, чем у прямого на конусе.
В декартовых координатах
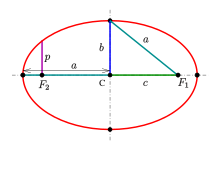
- a: большая полуось,
- b: малая полуось,
- c: линейный эксцентриситет,
- p: semi-latus rectum (обычно ℓ { displaystyle ell}
).
Стандартное уравнение
Стандартная форма эллипса в декартовых координатах предполагает, что начало координат находится в центре эллипса ось x — большая ось, и:
- фокусы — это точка F 1 = (c, 0), F 2 = (- c, 0) { displaystyle F_ {1} = (c, , 0), F_ { 2} = (- c, , 0)}
,
- вершинами являются V 1 = (a, 0), V 2 = (- a, 0) { displaystyle V_ {1} = (a, , 0), V_ {2} = (- a, , 0)}
.
для произвольной точки (x, y) { displaystyle (x, y)}




- (x — c) 2 + y 2 + (x + c) 2 + y 2 = 2 a. { displaystyle { sqrt {(xc) ^ {2} + y ^ {2}}} + { sqrt {(x + c) ^ {2} + y ^ {2}}} = 2a .}
Удаление радикалов подходящими квадратами и использованием b 2 = a 2 — c 2 { displaystyle b ^ {2} = a ^ {2} -c ^ {2}}
- x 2 a 2 + y 2 b 2 = 1, { displaystyle { frac {x ^ {2}} {a ^ {2}}} + { frac {y ^ {2}} {b ^ {2}}} = 1,}
или, решенное относительно y:
- y = ± baa 2 — x 2 = ± (a 2 — x 2) (1 — е 2). { displaystyle y = pm { frac {b} {a}} { sqrt {a ^ {2} -x ^ {2}}} = pm { sqrt { left (a ^ {2} — x ^ {2} right) left (1-e ^ {2} right)}}.}
Параметры ширины и высоты a, b { displaystyle a, ; b}




Из уравнения следует, что эллипс симметричен относительно осей координат и, следовательно, относительно начала координат.
Параметры
Главные оси
В этой статье большая и малая полуоси обозначаются a { displaystyle a}

В принципе, каноническое уравнение эллипса x 2 a 2 + y 2 b 2 = 1 { displaystyle { tfrac {x ^ {2 }} {a ^ {2}}} + { tfrac {y ^ {2}} {b ^ {2}}} = 1}




Линейный эксцентриситет
Это расстояние от центра к фокусу: c = a 2 — b 2 { displaystyle c = { sqrt {a ^ {2} -b ^ {2}}}}
Эксцентриситет
Эксцентриситет можно выразить как:
- e = ca = 1 — (ba) 2 { displaystyle e = { frac {c} {a}} = { sqrt {1- left ({ frac {b}) {a}} right) ^ {2}}}}
,
предположим г а>б. { displaystyle a>b.}

-lat7
Длина хорды, проходящей через один очаг, перпендикулярной большой оси, называется latus rectum. Половина ее составляет semi-latus rectum ℓ { displaystyle ell}
- ℓ знак равно b 2 a = a (1 — e 2). { Displaystyle ell = { frac {b ^ {2}} {a}} = a left (1-e ^ {2} right).}
Прямая полу-широта ℓ { displaystyle ell}
Касательная
Произвольная линия g { displaystyle g}


- x 1 a 2 x + y 1 b 2 y = 1. { displaystyle { frac {x_ {1}} {a ^ {2}}} x + { frac {y_ { 1}} {b ^ {2}}} y = 1.}
Векторное параметрическое уравнение касательной:
- x → = (x 1 y 1) + s (- y 1 a 2 Икс 1 б 2) { Displaystyle { vec {x}} = { begin {pmatrix} x_ {1} \ y_ {1} end {pmatrix}} + s { begin {pmatrix} ; ! — y_ {1} a ^ {2} \; x_ {1} b ^ {2} end {pmatrix}} }
с s ∈ R. { displaystyle s in mathbb {R} .}
Доказательство: Пусть (x 1, y 1) { displaystyle (x_ {1}, , y_ {1})}




- (x 1 + su) 2 a 2 + (y 1 + sv) 2 b 2 знак равно 1 ⟹ 2 s (x 1 ua 2 + y 1 vb 2) + s 2 (u 2 a 2 + v 2 b 2) = 0. { displaystyle { frac { left (x_ {1) } + su right) ^ {2}} {a ^ {2}}} + { frac { left (y_ {1} + sv right) ^ {2}} {b ^ {2}}} = 1 quad Longrightarrow quad 2s left ({ frac {x_ {1} u} {a ^ {2}}} + { frac {y_ {1} v} {b ^ {2}}} вправо) + s ^ {2} left ({ frac {u ^ {2}} {a ^ {2}}} + { frac {v ^ {2}} {b ^ {2}}} right) = 0 .}
- Тогда есть случаи:
- x 1 a 2 u + y 1 b 2 v = 0. { displaystyle { frac {x_ {1}} {a ^ {2}}} u + { frac {y_ {1}} {b ^ {2}}} v = 0.}
Затем строка g { displaystyle g}
и эллипс имеют только точка (x 1, y 1) { displaystyle (x_ {1}, , y_ {1})}
в общем, а g { displaystyle g}
— ка сательная. Касательное направление имеет перпендикулярный вектор (x 1 a 2 y 1 b 2) { displaystyle { begin {pmatrix} { frac {x_ {1}} {a ^ {2}}} { frac {y_ {1}} {b ^ {2}}} end {pmatrix}}}
, поэтому касательная линия имеет уравнение x 1 a 2 x + y 1 б 2 y = к { textstyle { frac {x_ {1}} {a ^ {2}}} x + { tfrac {y_ {1}} {b ^ {2}}} y = k}
для некоторых k { displaystyle k}
. <Времен738>(x 1, y 1) { displaystyle (x_ {1}, , y_ {1})}
находится на касательной и эллипсе, получаем k = 1 { displaystyle к = 1}
.
- x 1 a 2 u + y 1 b 2 v ≠ 0. { displaystyle { frac {x_ {1}} {a ^ {2}}} u + { frac {y_ {1) }} {b ^ {2}}} v neq 0.}
Тогда строка g { displaystyle g}
имеет вторую точку, общую с эллипсом, и является секансом.
- x 1 a 2 u + y 1 b 2 v = 0. { displaystyle { frac {x_ {1}} {a ^ {2}}} u + { frac {y_ {1}} {b ^ {2}}} v = 0.}
Используя (1), получаем, что (- y 1 a 2 x 1 b 2) { displaystyle { begin {pmatrix} -y_ {1} a ^ {2} x_ {1} b ^ {2} end {pmatrix}}}

Если (x 1, y 1) { displaystyle (x_ {1}, y_ {1})}



Сдвинутый эллипс
Если стандартный эллипс смещен так, чтобы его центр был (x ∘, y ∘) { displaystyle left (x _ { circ}, , y _ { circ} right)}
- (x — x ∘) 2 a 2 + (y — y ∘) 2 b 2 = 1. { displaystyle { frac { left (xx _ { circ} right) ^ {2}} {a ^ {2}}} + { frac { left (yy _ { circ} right)) ^ {2}} {b ^ {2}}} = 1 .}
Оси по-прежнему параллельны осям x и y.
Общий эллипс
В аналитической геометрии эллипс определяется как квадрика: набор точек (X, Y) { displaystyle (X, , Y)}
- AX 2 + BXY + CY 2 + DX + EY + F = 0 { displaystyle AX ^ {2} + BXY + CY ^ {2} + DX + EY + F = 0}
при условии B 2–4 AC < 0. {displaystyle B^{2}-4AC<0.}
Чтобы различать вырожденные случаи из невырожденного случая, пусть ∆ — детерминант
- ∆ = | A 1 2 B 1 2 D 1 2 B C 1 2 E 1 2 D 1 2 E F | = (AC — B 2 4) F + BED 4 — CD 2 4 — AE 2 4. { displaystyle Delta = { begin {vmatrix} A { frac {1} {2}} B { frac {1} {2}} D \ { frac {1} {2}} BC и { frac {1} {2}} E \ { frac {1} {2}} D { frac {1} {2}} EF end {vmatrix}} = left (AC — { frac {B ^ {2}} {4}} right) F + { frac {BED} {4}} — { frac {CD ^ {2}} {4}} — { frac {AE ^ {2}} {4}}.}
Тогда эллипс является невырожденным действительным эллипсом тогда и только тогда, когда C∆ < 0. If C∆>0, у нас есть мнимый эллипс, а если ∆ = 0, у нас есть точечный эллипс.
коэффициенты общих уравнений могут быть получены из известной большой полуоси a { displaystyle a}



- A = a 2 sin 2 θ + b 2 cos 2 θ B = 2 (b 2 — a 2) sin θ cos θ C = a 2 cos 2 θ + b 2 sin 2 θ D = — 2 A x ∘ — B y ∘ E = — B x ∘ — 2 C у ∘ F = A Икс ∘ 2 + В Икс ∘ Y ∘ + С Y ∘ 2 — а 2 б 2. { Displaystyle { begin {align} A = a ^ {2} sin ^ {2} theta + b ^ {2 } cos ^ {2} theta \ B = 2 left (b ^ {2} -a ^ {2} right) sin theta cos theta \ C = a ^ {2} cos ^ {2} theta + b ^ {2} sin ^ {2} theta D = — 2Ax _ { circ} -By _ { circ} \ E = — Bx _ { circ} -2Cy _ { circ} \ F = Ax _ { circ} ^ {2} + Bx _ { circ} y _ { circ} + Cy _ { circ} ^ {2} -a ^ {2} b ^ {2}. end {align}}}
Эти выражения могут быть получены из канонического уравнения x 2 a 2 + y 2 b 2 = 1 { displaystyle { tfrac {x ^ {2}} {a ^ {2 }}} + { tfrac {y ^ {2}} {b ^ {2}}} = 1}

- x = (X — x ∘) cos θ + (Y — y ∘) sin θ y = — (X — x ∘) sin θ + (Y — y ∘) cos θ. { Displaystyle { begin {выровнено} х = влево (X-х _ { circ} right) cos theta + left (Yy _ { circ} right) sin theta \ y = — left (Xx _ { circ} right) sin theta + left (Yy _ { circ} right) cos theta. end {align}}}
И наоборот, Параметры канонической формы могут быть получены из коэффициентов общей формы с помощью уравнений:
- a, b = — 2 (AE2 + CD 2 — BDE + (B 2 — 4 AC) F) ((A + C) ± (A — C) 2 + B 2) B 2 — 4 AC x ∘ = 2 CD — BEB 2 — 4 AC y ∘ = 2 AE — BDB 2 — 4 AC θ = {arctan (1 B (C — A — (A — C) 2 + B 2)) для B ≠ 0 0 для B = 0, A < C 90 ∘ for B = 0, A>C { displaystyle { begin {align} a, b = { frac {- { sqrt {2 { Big (} AE ^ {2} + CD ^ {2} -BDE + (B ^ {2} — 4AC) F { Big)} left ((A + C) pm { sqrt {(AC) ^ {2} + B ^ {2}}} right)}}} {B ^ {2} — 4AC}} \ x _ { circ} = { frac {2CD-BE} {B ^ {2} — 4AC}} \ [3pt] y _ { circ} = { frac {2AE- BD} {B ^ {2} -4AC}} \ [3pt] theta = { begin {cases} arctan left ({ frac {1} {B}} left (CA — { sqrt {(AC) ^ {2} + B ^ {2}}} right) right) { text {for}} B neq 0 \ 0 { text {for}} B = 0, A C \ end {case}} end {align}}}
Параметрическое представление
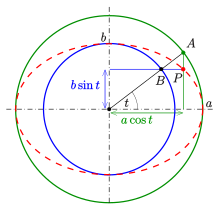

Δ u = 0,2 { displaystyle Delta u = 0, 2}

Стандартное параметрическое представление
Использование тригонометрические функции, параметрическое представление стандартного эллипса x 2 a 2 + y 2 b 2 = 1 { displaystyle { tfrac {x ^ {2}} {a ^ {2}}} + { tfrac {y ^ {2}} {b ^ {2}}} = 1}
- (x, y) = (a cos t, b sin t), 0 ≤ t < 2 π. {displaystyle (x,,y)=(acos t,,bsin t), 0leq t<2pi .}
Параметр t (который в астрономии называется эксцентрической аномалией ) не является углом (x (t), y ( t)) { displaystyle (x (t), y (t))}
Рациональное представление
С заменой u = tan (t 2) { textstyle u = tan left ({ frac {t} {2}} right) }
- cos t = 1 — u 2 U 2 + 1, T знак равно 2 uu 2 + 1 { displaystyle cos t = { frac {1- u ^ {2}} {u ^ {2} +1}} , quad sin t = { frac {2u} {u ^ {2} +1}}}
и рациональное параметрическое уравнение эллипса
- x (u) = a 1 — u 2 u 2 + 1 y (u) = 2 buu 2 + 1, — ∞ < u < ∞, {displaystyle {begin{aligned}x(u)=a{frac {1-u^{2}}{u^{2}+1}}\y(u)={frac {2bu}{u^{2}+1}}end{aligned}};,quad -infty
который покрывает любую точку эллипса x 2 a 2 + y 2 b 2 = 1 { displaystyle { tfrac {x ^ {2}} {a ^ {2}}} + { tfrac {y ^ {2}} {b ^ {2}}} = 1}

Для u ∈ [0, 1], { displaystyle u in [0, , 1 ],}![{displaystyle uin [0,,1],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c61b780db9ac550dd283876e16abe9c2cccdf8c3)

Рациональные представления конических сечений обычно используются в автоматизированном проектировании (см. кривая Безье ).
Наклон касательной как параметр
Параметрическое представление, в котором используется наклон m { displaystyle m}

- x → ′ (t) = (- грех t, b cos t) T → m = — ba cot t → cot t = — маб. { displaystyle { vec {x}} ‘(t) = (- a sin t, , b cos t) ^ { mathsf {T}} quad rightarrow quad m = — { frac { b} {a}} cot t quad rightarrow quad cot t = — { frac {ma} {b}}.}
С помощью тригонометрических формул получаем:
- cos t = детская кроватка t ± 1 + детская кроватка 2 t = — ma ± m 2 a 2 + b 2, sin t = 1 ± 1 + детская кроватка 2 t = b ± m 2 a 2 + b 2. { displaystyle cos t = { frac { cot t} { pm { sqrt {1+ cot ^ {2} t}}}} = { frac {-ma} { pm { sqrt { m ^ {2} a ^ {2} + b ^ {2}}}} , quad quad sin t = { frac {1} { pm { sqrt {1+ cot ^ {2) } t}}}} = { frac {b} { pm { sqrt {m ^ {2} a ^ {2} + b ^ {2}}}}}.}
Замена cos t { displaystyle cos t}

- c → ± (m) = ( — ma 2 ± m 2 a 2 + b 2, b 2 ± m 2 a 2 + b 2), m ∈ R. { displaystyle { vec {c}} _ { pm} (m) = left ( — { frac {ma ^ {2}} { pm { sqrt {m ^ {2} a ^ {2}) + b ^ {2}}}}}, ; { frac {b ^ {2}} { pm { sqrt {m ^ {2} a ^ {2} + b ^ {2}}}} right), , m in mathbb {R }.}
Здесь m { displaystyle m}



Уравнение касательной в точке c → ± (m) { displaystyle { vec {c}} _ { pm} (m)}



- y = mx ± m 2 a 2 + b 2. { displaystyle y = mx pm { sqrt {m ^ {2} a ^ {2} + b ^ {2}}} ;.}
Это описание касательных эллипса является важным инструментом для определения ортоптики эллипса. Ортоптическая статья содержит другое доказательство, без дифференциального исчисления и тригонометрических формул.
Общий эллипс

Другое определение эллипса использует аффинные преобразования :
- Любой эллипс является аффинным представлением единичной окружности с уравнением x 2 + y 2 = 1 { displaystyle x ^ {2} + y ^ {2} = 1}
.
- параметрическое представление
Аффинное преобразование евклидовой плоскости вид x → ↦ е → 0 + A x → { displaystyle { vec {x}} mapsto { vec {f}} ! _ {0} + A { vec {x}}}






- x → = p → (t) = f → 0 + f → 1 cos t + f → 2 sin t. { displaystyle { vec {x}} = { vec {p}} (t) = { vec {f}} ! _ {0} + { vec {f}} ! _ {1} cos t + { vec {f}} ! _ {2} sin t .}
Здесь f → 0 { displaystyle { vec {f}} ! _ {0}}

- вершины
Четыре вершины эллипса: p → (t 0), p → (t 0 ± π 2), p → (t 0 + π) { displaystyle { vec {p}} ( t_ {0}), ; { vec {p}} left (t_ {0} pm { tfrac { pi} {2}} right), ; { vec {p}} left (t_ {0} + pi right)}

- детская кроватка (2 t 0) = f → 1 2 — f → 2 2 2 f → 1 ⋅ f → 2. { displaystyle cot (2t_ {0}) = { гидроразрыв {{ vec {f}} ! _ {1} ^ {, 2} — { vec {f}} ! _ {2} ^ {, 2}} {2 { vec {f}} ! _ {1} cdot { vec {f}} ! _ {2}}}.}
(Если f → 1 ⋅ f → 2 = 0 { displaystyle { vec {f}} ! _ {1} cdot { vec {f}} ! _ {2} = 0}


- p → ′ (t) = — f → 1 sin t + f → 2 cos t. { displaystyle { vec {p}} , ‘(t) = — { vec {f}} ! _ {1} sin t + { vec {f}} ! _ {2} cos t .}
При параметре вершины t = t 0 { displaystyle t = t_ {0}}
- 0 = p → ′ (t) ⋅ (p → (t) — f → 0) = (- f → 1 sin t + f → 2 cos t) ⋅ (f → 1 cos t + f → 2 sin т). { displaystyle 0 = { vec {p}} ‘(t) cdot left ({ vec {p}} (t) — { vec {f}} ! _ {0} right) = left (- { vec {f}} ! _ {1} sin t + { vec {f}} ! _ {2} cos t right) cdot left ({ vec {f} } ! _ {1} cos t + { vec {f}} ! _ {2} sin t right).}
Расширение и применение тождеств cos 2 t — sin 2 t знак равно соз 2 T, 2 грех T соз T знак равно грех 2 t { displaystyle cos ^ {2} t- sin ^ {2} t = cos 2t, 2 sin t cos t = sin 2t}

- неявного представления
Решение параметрического представления для cos т, грех т { displaystyle ; cos t, sin t ;}

- det (x → — f → 0, f → 2) 2 + det (е → 1, x → — f → 0) 2 — det (f → 1, f → 2) 2 = 0 { displaystyle det ({ vec {x}} ! — ! { vec { f}} ! _ {0}, { vec {f}} ! _ {2}) ^ {2} + det ({ vec {f}} ! _ {1}, { vec { x}} ! — ! { Vec {f}} ! _ {0}) ^ {2} — det ({ vec {f}} ! _ {1}, { vec {f} } ! _ {2}) ^ {2} = 0}
.
- Определение эллипса в этом разделе дает параметрическое представление произвольноголипса, даже в пространстве, если можно f → 0, f → 1, е → 2 { displaystyle { vec {f}} ! _ {0}, { vec {f}} ! _ {1}, { vec {f}} ! _ {2}}
быть векторми в дизайне.
Полярные формы
Полярные формы относительно центра
Полярные координаты с центром в центре.
В полярных координатах, с началом в центре эллипса и с угловой координатой θ { displaystyle theta}
, измеренной от большой оси, уравнение эллипса имеет вид
- р (θ) знак равно ab (b соз θ) 2 + (грех θ) 2 знак равно б 1 — (е соз θ) 2 { displaystyle r ( theta) = { frac {ab} { sqrt {(b cos theta) ^ {2} + (a sin theta) ^ {2}}}} = { frac {b} { sqrt {1- (e cos theta) ^ { 2}}}}
- r (θ) = a (1 — e 2) 1 ± e cos θ { displaystyle r ( theta) = { frac {a (1-e ^ {2})} {1 pm e cos theta}}}
- r = a (1 — e 2) 1 — e cos (θ — ϕ). { displaystyle r = { frac {a (1-e ^ {2})} {1-e cos ( theta — phi)}}.}
- Для произвольной точки P { displaystyle P}
эллипса отношение расстояния до одного фокуса и соответствующей направляющей (см. Диаграмму) равно эксцентриситету:
- | P F 1 | | P l 1 | = | P F 2 | | P l 2 | = е = с а. { displaystyle { frac { left | PF_ {1} right |} { left | Pl_ {1} right |}} = { frac { left | PF_ {2} right |} { left | Pl_ {2} right |}} = e = { frac {c} {a}} .}
- | P F 1 | | P l 1 | = | P F 2 | | P l 2 | = е = с а. { displaystyle { frac { left | PF_ {1} right |} { left | Pl_ {1} right |}} = { frac { left | PF_ {2} right |} { left | Pl_ {2} right |}} = e = { frac {c} {a}} .}
- | P F 1 | 2 — с 2 а 2 | P l 1 | 2 = 0. { displaystyle left | PF_ {1} right | ^ {2} — { frac {c ^ {2}} {a ^ {2}}} left | Pl_ {1} right | ^ {2} = 0 .}
- Для любой точки F { displaystyle F}
(фокус), любая строка l { displaystyle l}
(directrix) не через F { displaystyle F}
и любое действительное число e { displaystyle e}
с 0 < e < 1, {displaystyle 0
эллипс — это геометрическое место точек, для которых отношение расстояний до точки и линии равно e, { displaystyle e, }
то есть:
- E = {P | | P F | | P l | = e}. { Displaystyle E = left {P left | { frac {| PF |} {| Pl |}} = e right. right }.}
- E = {P | | P F | | P l | = e}. { Displaystyle E = left {P left | { frac {| PF |} {| Pl |}} = e right. right }.}
- Доказательство
- (x — f) 2 + y 2 = e 2 (x + fe) 2 = (ex + f) 2 { displaystyle (xf) ^ {2 } + y ^ {2} = e ^ {2} left (x + { frac {f} {e}} right) ^ {2} = (ex + f) ^ {2}}
и x 2 (e 2-1) + 2 xf (1 + e) - y 2 = 0. { displaystyle x ^ {2} left (e ^ {2} -1 right) + 2xf (1 + e) -y ^ {2} = 0.}
- x 2 (e 2-1) + 2 px — y 2 = 0. { displaystyle x ^ {2} left (e ^ {2} -1 right) + 2px- y ^ {2} = 0.}
- (x — a) 2 a 2 + y 2 b 2 = 1, { displaystyle { frac {(xa) ^ {2}} {a ^ {2}}} + { frac {y ^ {2}} {b ^ {2}} = 1 ,}
- Общий эллипс
- (x — f 1) 2 + (y — f 2) 2 = e 2 (ux + vy + w) 2 u 2 + v 2. { displaystyle left (x-f_ {1} right) ^ {2} + left (y-f_ {2} right) ^ {2} = e ^ {2} { frac { left (ux + vy + w right) ^ {2}} {u ^ {2} + v ^ {2}}} .}
- Нормаль в точке P { displaystyle P}
делит пополам угол между линиями PF 1 ¯, PF 2 ¯ { displaystyle { overline { PF_ {1}}}, , { overline {PF_ {2}}}}
.
- Доказательство
- Приложение
- Передние параллельные хорд лежат на диаметре.
- Определение
- Два диаметра P 1 Q 1 ¯, P 2 Q 2 ¯ { displaystyle { overline {P_ {1} Q_ {1}}}, , { overline {P_ {2} Q_ {2}}}}
эллипса сопряжены, если касательные в точке P 1 { displaystyle P_ {1}}
и Q 1 { displaystyle Q_ { 1}}
параллельны P 2 Q 2 ¯ { displaystyle { overline {P_ {2} Q_ {2}}}}
.
- x → = p → (t) = f → 0 + f → 1 cos t + f → 2 sin t, { displaystyle { vec {x}} = { vec {p}} (t) = { vec {f}} ! _ {0} + { vec {f}} ! _ {1} cos t + { vec {f}} ! _ {2} sin t,}
- Пусть c 1 { displaystyle c_ {1}}
и c 2 { displaystyle c_ {2}}
быть половинками двух сопряженных диаметров (см. Диаграмму), тогда
- c 1 2 + c 2 2 = a 2 + b 2 { displaystyle c_ {1} ^ {2} + c_ {2} ^ {2} = a ^ {2} + b ^ {2}}
,
- треугольник, образованный c 1, c 2 { displaystyle c_ {1}, , c_ {2}}
, имеет постоянную площадь A Δ = 1 2 ab { textstyle A _ { Delta} = { frac {1} {2}} ab}
- параллелограмм касательных, примыкающих к данным сопряженным диаметром, имеет Площадь 12 = 4 пр. { displaystyle { text {Area}} _ {12} = 4ab .}
- c 1 2 + c 2 2 = a 2 + b 2 { displaystyle c_ {1} ^ {2} + c_ {2} ^ {2} = a ^ {2} + b ^ {2}}
- Доказательство
- p → (t) = (a cos t, b грех t) { displaystyle { vec {p}} (t) = (a cos t, , b sin t)}
.
- | c → 1 | 2 + | c → 2 | 2 знак равно ⋯ знак равно а 2 + Ь 2. { displaystyle left | { vec {c}} _ {1} right | ^ {2} + left | { vec {c}} _ {2} right | ^ {2} = cdots = a ^ {2} + b ^ {2} .}
- A Δ = 1 2 det (c → 1, c → 2) = ⋯ = 1 2 ab { displaystyle A _ { Дельта} = { frac {1} {2}} det left ({ vec {c}} _ {1}, , { vec {c}} _ {2} справа) = cdots = { frac {1} {2}} ab}
- Площадь 12 = 4 a b. { displaystyle { text {Area}} _ {12} = 4ab .}
- Нарисуйте две окружности в центре эллипса с радиусами a, b { displaystyle a, b}
и осями эллипса.
- Проведите линию через центр, которая пересекает два круга в точке A { displaystyle A}
и B { displaystyle B}
соответственно..
- Проведите линию через A { displaystyle A}
, которая параллельна малой оси, и линию через B { displaystyle B}
, которая параллельна большой оси. Эти линии пересекаются в точке эллипса (см. Диаграмму).
- Повторите шаги (2) и (3) с разными линиями через центр.
Метод де Ла Хира
Анимация метода
- (a cos t, b sin t) { displaystyle (a cos t, , b sin t)}
- Метод 1
- полосы бумаги длиной a + b { displaystyle a + b}
.
Конструкция бумажной ленты 1
Эллипсы с парой Туси. Два примера: красный и голубой.
Вариант метода 1 полосы бумаги
Анимация варианта метода 1 полосы бумаги
- Метод 2
- a полоска бумаги длиной a { displaystyle a}
.
Траммель Архимеда (принцип)
Эллипсограф из-за Бенджамина Брамера
Вариант метода бумажной полосы 2
- отмечает точку H = (a, b) { displaystyle H = (a, , b)}
и нарисуйте отрезок линии V 1 V 3, { displaystyle V_ {1} V_ {3} ,}
- нарисуйте линию через H { displaystyle H}
, которая перпендикулярна линии V 1 V 3, { displaystyle V_ {1} V_ {3} ,}
- пересечение точки этой линии с осями центрами соприкасающихся окружностей.
- Даны два карандаша B (U), B (V) { displaystyle B (U), , B (V)}
линий в двух точках U, V { displaystyle U, , V}
(все строки, содержащие U displaystyle U}
и V { displaystyle V}
соответственно) и проекционное, но не перспективное отображение π { displaystyle pi}
из B (U) { displaystyle B (U)}
на B (V) { displaystyle B (V)}
, то точки пересечения соответствующих прямых образуют невырожденное проективное коническое сечение.
- Для четырех точек P i = (xi, yi), i = 1, 2, 3, 4, { displaystyle P_ {i} = left (x_ {i}, , y_ {i} right), i = 1, , 2, , 3, , 4, ,}
(см. диаграмму) верно следующее утверждение:
- Четыре точки находятся на окружности тогда и только тогда, когда углы равны P 3 { displaystyle P_ {3}}
и P 4 { displaystyle P_ {4}}
равны.
- Чтобы измерить угол между двумя линиями с помощью уравнений y = m 1 Икс + d 1, Y знак равно м 2 Икс + d 2, м 1 ≠ м 2, { displaystyle y = m_ {1} x + d_ {1}, y = m_ {2} x + d_ {2}, m_ {1} neq m_ {2},}
используется частное:
- 1 + m 1 m 2 m 2 — m 1 = cot θ. { displaystyle { frac {1 + m_ {1} m_ {2}} {m_ {2} -m_ {1}}} = cot theta .}
- 1 + m 1 m 2 m 2 — m 1 = cot θ. { displaystyle { frac {1 + m_ {1} m_ {2}} {m_ {2} -m_ {1}}} = cot theta .}
- точки находятся на окружности, если и только если углы равны P 3 { displaystyle P_ {3}}
и P 4 { displaystyle P_ {4}}
равны. В терминах измерения угла выше это означает:
- (x 4 — x 1) (x 4 — x 2) + (y 4 — y 1) (y 4 — y 2) (y 4 — y 1) (x 4 — x 2) — (y 4 — y 2) (x 4 — x 1) = (x 3 — x 1) (x 3 — x 2) + (y 3 — y 1) (y 3 — y 2) (y 3 — y 1) (x 3 — x 2) — (y 3 — y 2) (x 3 — x 1). { displaystyle { frac {(x_ {4} -x_ {1}) (x_ {4} -x_ {2}) + (y_ {4} -y_ {1}) (y_ {4} -y_ {2 })} {(y_ {4} -y_ {1}) (x_ {4} -x_ {2}) — (y_ {4} -y_ {2}) (x_ {4} -x_ {1})} } = { frac {(x_ {3} -x_ {1}) (x_ {3} -x_ {2}) + (y_ {3} -y_ {1}) (y_ {3} -y_ {2})} {(y_ {3} -y_ {1}) (x_ {3} -x_ {2}) — (y_ {3} -y_ {2}) (x_ {3} -x_ {1})}}.}
- (x 4 — x 1) (x 4 — x 2) + (y 4 — y 1) (y 4 — y 2) (y 4 — y 1) (x 4 — x 2) — (y 4 — y 2) (x 4 — x 1) = (x 3 — x 1) (x 3 — x 2) + (y 3 — y 1) (y 3 — y 2) (y 3 — y 1) (x 3 — x 2) — (y 3 — y 2) (x 3 — x 1). { displaystyle { frac {(x_ {4} -x_ {1}) (x_ {4} -x_ {2}) + (y_ {4} -y_ {1}) (y_ {4} -y_ {2 })} {(y_ {4} -y_ {1}) (x_ {4} -x_ {2}) — (y_ {4} -y_ {2}) (x_ {4} -x_ {1})} } = { frac {(x_ {3} -x_ {1}) (x_ {3} -x_ {2}) + (y_ {3} -y_ {1}) (y_ {3} -y_ {2})} {(y_ {3} -y_ {1}) (x_ {3} -x_ {2}) — (y_ {3} -y_ {2}) (x_ {3} -x_ {1})}}.}
- Как следствие, получается уравнение для круга, определяемого тремя неколлинеарными точками P i = (xi, yi) { displaystyle P_ { i} = left (x_ {i}, , y_ {i} right)}
:
- (x — x 1) (x — x 2) + (y — y 1) (y — y 2) ( y — y 1) (x — x 2) — (y — y 2) (x — x 1) = (x 3 — x 1) (x 3 — x 2) + (y 3 — y 1) (y 3 — y 2) (y 3 — y 1) (x 3 — x 2) — (y 3 — y 2) (x 3 — x 1). { displaystyle { frac {({ color {red} x} -x_ {1}) ({ color {red} x} -x_ {2}) + ({ color {red} y} -y_ { 1}) ({ цвет {красный} y} -y_ {2})} {({ color {красный} y} -y_ {1}) ({ color {красный} x} -x_ {2}) — ({ color {red} y} -y_ {2}) ({ color {red} x} -x_ {1})}} = { frac {(x_ {3} -x_ {1}) ( x_ {3} -x_ {2}) + (y_ {3} -y_ {1}) (y_ {3} -y_ {2})} {(y_ {3} -y_ {1}) (x_ {3 } -x_ {2}) — (y_ {3} -y_ {2}) (x_ {3} -x_ {1})}}.}
- (x — x 1) (x — x 2) + (y — y 1) (y — y 2) ( y — y 1) (x — x 2) — (y — y 2) (x — x 1) = (x 3 — x 1) (x 3 — x 2) + (y 3 — y 1) (y 3 — y 2) (y 3 — y 1) (x 3 — x 2) — (y 3 — y 2) (x 3 — x 1). { displaystyle { frac {({ color {red} x} -x_ {1}) ({ color {red} x} -x_ {2}) + ({ color {red} y} -y_ { 1}) ({ цвет {красный} y} -y_ {2})} {({ color {красный} y} -y_ {1}) ({ color {красный} x} -x_ {2}) — ({ color {red} y} -y_ {2}) ({ color {red} x} -x_ {1})}} = { frac {(x_ {3} -x_ {1}) ( x_ {3} -x_ {2}) + (y_ {3} -y_ {1}) (y_ {3} -y_ {2})} {(y_ {3} -y_ {1}) (x_ {3 } -x_ {2}) — (y_ {3} -y_ {2}) (x_ {3} -x_ {1})}}.}
- (x — 2) x + y (y — 1) yx — (y — 1) (х — 2) знак равно 0 { displaystyle { frac {(x-2) x + y (y-1)} {yx- (y-1) (x-2)}} = 0}
, который можно переформатировать в (x — 1) 2 + (y — 1 2) 2 = 5 4. { displaystyle (x-1) ^ {2} + left (y — { tfrac {1} {2}} right) ^ {2} = { tfrac {5} {4}} .}
- (x → — x → 1) ⋅ (x → — x → 2) det (x → — x → 1, x → — x → 2) = (x → 3 — x → 1) ⋅ (x → 3 — x → 2) det (x → 3 — x → 1, x → 3 — x → 2). { displaystyle { frac { left ({ color {red} { vec {x}}} — { vec {x}} _ {1} right) cdot left ({ color {red}) { vec {x}}} — { vec {x}} _ {2} right)} { det left ({ color {red} { vec {x}}} — { vec {x }} _ {1}, { color {red} { vec {x}}} — { vec {x}} _ {2} right)}} = { frac { left ({ vec { x}} _ {3} — { vec {x}} _ {1} right) cdot left ({ vec {x}} _ {3} — { vec {x}} _ {2} right)} { det left ({ vec {x}} _ {3} — { vec {x}} _ {1}, { vec {x}} _ {3} — { vec { x}} _ {2} right)}}.}
- [1 y 1 — y 2 x 1 — x 2 x 1 — x 3 y 1 — y 3 1] [x ∘ y ∘] = [x 1 2 — x 2 2 + y 1 2 — y 2 2 2 (x 1 — x 2) y 1 2 — y 3 2 + x 1 2 — x 3 2 2 (y 1 — y 3)]. { displaystyle { begin {bmatrix} 1 { frac {y_ {1} -y_ {2}} {x_ {1} -x_ {2}}}\ { frac {x_ {1} -x_ {3)}} {y_ {1} -y_ {3}}} 1 end {bmatrix}} { begin {bmatrix} x _ { circ} y _ { circ} end {bmatrix}} = { begin {bmatrix} { frac {x_ {1} ^ {2} -x_ {2} ^ {2} + y_ {1} ^ {2} -y_ {2} ^ {2}} {2 (x_ {1} — x_ {2})}} \ { frac {y_ {1} ^ {2} -y_ {3} ^ {2} + x_ {1} ^ {2} -x_ {3} ^ {2}} {2 (y_ {1} -y_ {3})}} end {bmatrix}}.}
- r = (x 1 — x ∘) 2 + (y 1 — y ∘) 2 = (x 2 — x ∘) 2 + (y 2 — y) 2 = (x 3 — x ∘) 2 + ( у 3 — у) 2. { displaystyle r = { sqrt { left (x_ {1} -x _ { circ} right) ^ {2} + left (y_ {1} -y _ { circ} right) ^ {2}}} = { sqrt { left (x_ {2} -x _ { circ} right) ^ {2} + left (y_ {2} -y _ { circ} right) ^ {2}}} = { sqrt { left (x_ {3} -x _ { circ} right) ^ {2} + left (y_ {3} -y _ { circ} right) ^ {2}}}.}
- q = a 2 b 2 = 1 1 — e 2, { displaystyle { color {blue} q} = { frac {a ^ {2}} {b ^ {2}}} = { frac {1} {1-e ^ {2}}},}
- (x — x ∘) 2 + q (y — y ∘) 2 знак равно a 2, { displaystyle left (xx _ { circ} right) ^ {2} + { color {blue} q} , left (yy _ { circ} right) ^ {2} = a ^ {2},}
- Для этого семейства эллипсов вводится следующее q-аналог Измерение угла между двумя линиями с помощью соотношений y = m 1 x + d 1, y = m 2 Икс + d 2, м 1 ≠ м 2 { displaystyle y = m_ {1} x + d_ {1}, y = m_ {2} x + d_ {2}, m_ {1} neq m_ {2}}
используется частное:
- 1 + qm 1 m 2 m 2 — m 1. { Displaystyle { frac {1 + { color {blue} q} ; m_ {1} m_ {2}} {m_ {2} -m_ {1}}} .}
- 1 + qm 1 m 2 m 2 — m 1. { Displaystyle { frac {1 + { color {blue} q} ; m_ {1} m_ {2}} {m_ {2} -m_ {1}}} .}
- Дано четыре точка п i = (xi, yi), i = 1, 2, 3, 4 { displaystyle P_ {i} = left (x_ {i}, , y_ {i} right), i = 1, , 2, , 3, , 4}
, три из них на прямой (см. диаграмму).
- Четыре точки находятся на эллипсе с уравнением (Икс — Икс ∘) 2 + Q (Y — Y ∘) 2 = a 2 { displaystyle (xx _ { circ}) ^ {2} + { color {blue} q} , (yy _ { circ}) ^ {2} = a ^ {2}}
тогда и только тогда, когда углы в P 3 { displaystyle P_ {3}}
и P 4 { displaystyle P_ {4}}
равны в смысле измерения выше, то есть если
- (x 4 — x 1) (x 4 — x 2) + q (y 4 — y 1) (y 4 — y 2) (y 4 — y 1) (x 4 — x 2) — (y 4 — y 2) (x 4 — x 1) = (x 3 — x 1) (x 3 — x 2) + q (y 3 — y 1) (y 3 — y 2) (y 3 — y 1) (x 3 — x 2) — (y 3 — y 2) (х 3 — х 1). { displaystyle { frac {(x_ {4} -x_ {1}) (x_ {4} -x_ {2}) + { color {blue} q} ; (y_ {4} -y_ {1})) (y_ {4} -y_ {2})} {(y_ {4} -y_ {1}) (x_ {4} -x_ {2}) — (y_ {4} -y_ {2}) (x_ {4} -x_ {1})}} = { frac {(x_ {3} -x_ {1}) (x_ {3} -x_ {2}) + { color {blue} q} ; (y_ {3} -y_ {1}) (y_ {3} -y_ {2})} {(y_ {3} -y_ {1}) (x_ {3} -x_ {2}) — (y_ { 3} -y_ {2}) (x_ {3} -x_ {1})}} .}
- (x 4 — x 1) (x 4 — x 2) + q (y 4 — y 1) (y 4 — y 2) (y 4 — y 1) (x 4 — x 2) — (y 4 — y 2) (x 4 — x 1) = (x 3 — x 1) (x 3 — x 2) + q (y 3 — y 1) (y 3 — y 2) (y 3 — y 1) (x 3 — x 2) — (y 3 — y 2) (х 3 — х 1). { displaystyle { frac {(x_ {4} -x_ {1}) (x_ {4} -x_ {2}) + { color {blue} q} ; (y_ {4} -y_ {1})) (y_ {4} -y_ {2})} {(y_ {4} -y_ {1}) (x_ {4} -x_ {2}) — (y_ {4} -y_ {2}) (x_ {4} -x_ {1})}} = { frac {(x_ {3} -x_ {1}) (x_ {3} -x_ {2}) + { color {blue} q} ; (y_ {3} -y_ {1}) (y_ {3} -y_ {2})} {(y_ {3} -y_ {1}) (x_ {3} -x_ {2}) — (y_ { 3} -y_ {2}) (x_ {3} -x_ {1})}} .}
- Как следствие, уравнение для эллипса, определяемое тремя неколлинеарными точками P i = (xi, yi) { displaystyle P_ {i} = left (x_ {i }, , y_ {i} right)}
:
- (x — x 1) (x — x 2) + q (y — y 1) (y — y 2) (y — y 1) (x — x 2) — (y — y 2) (x — x 1) = (x 3 — x 1) (x 3 — x 2) + q (y 3 — y 1) (y 3 — y 2) (y 3 — y 1) (x 3 — x 2) — (y 3 — y 2) (x 3 — x 1). { displaystyle { frac {({ color {red} x} -x_ {1}) ({ color {red} x} -x_ {2}) + { color {blue} q} ; ({ color {red} y} -y_ {1}) ({ color {red} y} -y_ {2})} {({ color {red} y} -y_ {1}) ({ цвет {красный} x} -x_ {2}) — ({ color {red} y} -y_ {2}) ({ color {red} x} -x_ {1})}} = { frac { (x_ {3} -x_ {1}) (x_ {3} -x_ {2}) + { color {blue} q} ; (y_ {3} -y_ {1}) (y_ {3} -y_ {2})} {(y_ {3} -y_ {1}) (x_ {3} -x_ {2}) — (y_ { 3} -y_ {2}) (x_ {3} -x_ {1})}} .}
- (x — x 1) (x — x 2) + q (y — y 1) (y — y 2) (y — y 1) (x — x 2) — (y — y 2) (x — x 1) = (x 3 — x 1) (x 3 — x 2) + q (y 3 — y 1) (y 3 — y 2) (y 3 — y 1) (x 3 — x 2) — (y 3 — y 2) (x 3 — x 1). { displaystyle { frac {({ color {red} x} -x_ {1}) ({ color {red} x} -x_ {2}) + { color {blue} q} ; ({ color {red} y} -y_ {1}) ({ color {red} y} -y_ {2})} {({ color {red} y} -y_ {1}) ({ цвет {красный} x} -x_ {2}) — ({ color {red} y} -y_ {2}) ({ color {red} x} -x_ {1})}} = { frac { (x_ {3} -x_ {1}) (x_ {3} -x_ {2}) + { color {blue} q} ; (y_ {3} -y_ {1}) (y_ {3} -y_ {2})} {(y_ {3} -y_ {1}) (x_ {3} -x_ {2}) — (y_ { 3} -y_ {2}) (x_ {3} -x_ {1})}} .}
- (x — 2) Икс + 4 Y (Y — 1) Yx — (Y — 1) (X — 2) = 0 { Displaystyle { frac {(x-2) x + 4y (Y-1)} {yx- (y- 1) (x-2)}} = 0}
и после преобразования (x — 1) 2 2 + (y — 1 2) 2 1 2 = 1. { displaystyle { frac {(x-1) ^ {2}} {2}} + { frac { left (y — { frac {1} {2}} right) ^ {2}} { frac {1} { 2}}} = 1.}
- (x → — x → 1) ∗ (x → — x → 2) det (x → — x → 1, x → — x → 2) знак равно (x → 3 — x → 1) ∗ (x → 3 — x → 2) det (x → 3 — x → 1, x → 3 — x → 2), { displaystyle { frac { left ({ color {red} { vec {x}}} — { vec {x}} _ {1} right) * left ({ color {red} { vec { x}}} — { vec {x}} _ {2} right)} { det left ({ color {красный} { vec {x}}} — { vec {x}} _ { 1}, { color {red} { vec {x}}} — { vec {x}} _ {2} right)}} = { frac { left ({ vec {x}} _ {3} — { vec {x}} _ {1} righ t) * left ({ vec {x}} _ {3} — { vec {x}} _ {2} right)} { det left ({ vec {x}} _ {3} — { vec {x}} _ {1}, { vec {x}} _ {3} — { vec {x}} _ {2} right)}},}
- точка P 1 = (x 1, y 1) ≠ (0, 0) { displaystyle P_ {1} = left (x_ {1}, , y_ {1} right) neq (0, , 0)}
отображается в строке x 1 xa 2 + y 1 yb 2 = 1 { displaystyle { tfrac {x_ {1} x} {a ^ {2}}} + { tfrac {y_ {1} y} {b ^ {2}}} = 1}
, а не через центр эллипса.
- линию y = mx + d, d ≠ 0 { displaystyle y = mx + d, d neq 0}
на точку (- ma 2 d, б 2 d) { displaystyle left (- { tfrac {ma ^ {2}} {d}}, , { tfrac {b ^ {2}} {d}} справа)}
и
- строка x = c, c ≠ 0 { displaystyle x = c, c neq 0}
на точку (а 2 с, 0). { displaystyle left ({ tfrac {a ^ {2}} {c}}, , 0 right) .}
- Для точки (полюса) на эллипсе полярность является касательной в этой точке (см. Диаграмму: P 1, p 1 { displaystyle P_ {1}, , p_ {1}}
).
- Для полюса P { displaystyle P}
вне эллипса точки пересечения его полярные с эллипсом — это точки касания двух касательных, проходящих через P { displaystyle P}
(см. диаграмму: P 2, p 2 { displaystyle P_ {2}, , p_ {2}}
).
- Для точки внутри эллипса полярная точка не имеет общей точки с эллипсом (см. диаграмму: F 1, l 1 { displaystyle F_ {1}, , l_ {1 }}
).
- Точка пересечения двух поляр — это полюс линии, проходящей через их полюса.
- Фокусы (c, 0), { displaystyle (c, , 0),}
и (- c, 0) { displaystyle (-c, , 0)}
соответственно и директрисы x = a 2 c { displaystyle x = { tfrac {a ^ {2}} {c}}}
и x = — a 2 c { displaystyle x = — { tfrac {a ^ {2}} {c}}}
соответственно относятся к парам полюса и полюса.
- Эллипс = π ab { displaystyle A _ { text {ellipse}} = pi ab}
- Эллипс = ∫ — aa 2 b 1 — x 2 a 2 dx = ba ∫ — aa 2 a 2 — x 2 dx. { displaystyle { begin {align} A _ { text {ellipse}} = int _ {- a} ^ {a} 2b { sqrt {1 — { frac {x ^ {2}} {a ^ {2}}}}} , dx \ = { frac {b} {a}} int _ {- a} ^ {a} 2 { sqrt {a ^ {2} -x ^ { 2}}} , dx. end {align}}}
- A эллипс = ba π a 2 = π a b. { displaystyle A _ { text {ellipse}} = { frac {b} {a}} pi a ^ {2} = pi ab.}
- C = 4 a ∫ 0 π / 2 1 — е 2 грех 2 θ d θ = 4 a E (e) { displaystyle C , = , 4a int _ {0} ^ { pi / 2} { sqrt {1-e ^ {2} sin ^ {2} theta}} d theta , = , 4a , E (e)}
- E (e) = ∫ 0 π / 2 1 — е 2 грех 2 θ d θ { Displaystyle E (e) , = , int _ {0} ^ { pi / 2} { sqrt {1-e ^ {2} sin ^ {2} theta}} d theta}
- C = 2 π a [1 — (1 2) 2 e 2 — (1 ⋅ 3 2 ⋅ 4) 2 e 4 3 — (1 ⋅ 3 ⋅ 5 2 ⋅ 4 ⋅ 6) 2 e 6 5 — ⋯] = 2 π a [1 — ∑ n = 1 ∞ ((2 n — 1) !! (2 n) !!) 2 e 2 n 2 n — 1] = — 2 π a ∑ N знак равно 0 ∞ ((2 n — 1) !! (2 n) !!) 2 e 2 n 2 n — 1, { Displaystyle { begin {align} C = 2 pi a left [{1- left ({ frac {1} {2}} right) ^ {2} e ^ {2} — left ({ frac {1 cdot 3} {2 cdot 4}}) right) ^ {2} { frac {e ^ {4}} {3}} — left ({ frac {1 cdot 3 cdot 5} {2 cdot 4 cdot 6}} right) ^ {2} { frac {e ^ {6}} {5}} — cdots} right] \ = 2 pi a left [1- sum _ { n = 1} ^ { infty} left ({ frac {(2n-1) !!} {(2n) !!}} right) ^ {2} { frac {e ^ {2n}} { 2n-1}} right] \ = — 2 pi a sum _ {n = 0} ^ { infty} left ({ frac {(2n-1) !!} {(2n)! !}} right) ^ {2} { frac {e ^ {2n}} {2n-1}}, end {align}}}
- C = π (a + b) ∑ n = 0 ∞ ((2 n — 3) !! 2 nn !) 2 hn = π (a + b) [1 + h 4 + ∑ n = 2 ∞ ((2 n — 3) !! 2 nn!) 2 hn] = π (a + b) [1 + ∑ n = 1 ∞ ((2 n — 1) !! 2 nn!) 2 hn (2 n — 1) 2]. { displaystyle { begin {align} C = pi (a + b) sum _ {n = 0} ^ { infty} left ({ frac {(2n-3) !!} {2 ^ {n} n!}} right) ^ {2} h ^ {n} \ = pi (a + b) left [1 + { frac {h} {4}} + sum _ { n = 2} ^ { infty} left ({ frac {(2n-3) !!} {2 ^ {n} n!}} Right) ^ {2} h ^ {n} right] = pi (a + b) left [1+ sum _ {n = 1} ^ { infty} left ({ frac {(2n-1) !!} {2 ^ {n} n !}} right) ^ {2} { frac {h ^ {n}} {(2n-1) ^ {2}}} right]. end {align}}}
- C ≈ π [3 (a + b) — (3 a + b) (a + 3 b)] = π [3 (a + b) — 10 ab + 3 (a 2 + b 2) ] { displaystyle C приблизительно pi { biggl [} 3 (a + b) — { sqrt {(3a + b) (a + 3b)}} { biggr]} = pi { biggl [} 3 (a + b) — { sqrt {10ab + 3 left (a ^ {2} + b ^ {2} right)}} { biggr]}}
- C ≈ π ( а + б) (1 + 3 ч 10 + 4 — 3 ч). { displaystyle C приблизительно pi left (a + b right) left (1 + { frac {3h} {10 + { sqrt {4-3h}}}} right).}
- y = b 1 — x 2 a 2. { displaystyle y = b { sqrt {1 — { frac {x ^ {2}} {a ^ {2}}}}}.}
- s = — b ∫ arccos x 1 a arccos x 2 a 1 — (1 — a 2 b 2) sin 2 zdz. { displaystyle s = -b int _ { arccos { frac {x_ {1}} {a}}} ^ { arccos { frac {x_ {2}} {a}}} { sqrt {1 — left (1 — { frac {a ^ {2}} {b ^ {2}}} right) sin ^ {2} z}} , dz.}
- s знак равно — б [E (z | 1 — a 2 b 2)] arccos x 1 a arccos x 2 a { displaystyle s = -b left [E left (z ; { Biggl |} ; 1 — { frac {a ^ {2}} {b ^ {2}}} right) right] _ { arccos { frac {x_ {1}} {a}}} ^ { arccos { frac {x_ {2}} {a}}}}
- 2 π b ≤ C ≤ 2 π a, π (a + b) ≤ C ≤ 4 (a + b), 4 a 2 + b 2 ≤ C ≤ 2 π a 2 + b 2. { Displaystyle { begin {align} 2 pi b leq C leq 2 pi a, \ pi (a + b) leq C leq 4 (a + b), \ 4 { sqrt {a ^ {2} + b ^ {2}}} leq C leq { sqrt {2}} pi { sqrt {a ^ {2} + b ^ {2}}}. end {выровнен}}}
- ρ = a 2 b 2 (x 2 a 4 + y 2 b 4) 3 2 = 1 a 4 b 4 (a 4 y 2 + b 4 x 2) 3. { displaystyle rho = a ^ {2} b ^ {2} left ({ frac {x ^ {2}} {a ^ {4}}} + { frac {y ^ {2}} {b ^ {4}}} right) ^ { frac {3} {2}} = { frac {1} {a ^ {4} b ^ {4}}} { sqrt { left (a ^ { 4} y ^ {2} + b ^ {4} x ^ {2} right) ^ {3}}} .}
- ρ 0 = b 2 a = p, (± c 2 a | 0). { displaystyle rho _ {0} = { frac {b ^ {2}} {a}} = p , qquad left ( pm { frac {c ^ {2}} {a}} , { bigg |} , 0 right) .}
- ρ 1 = a 2 b, (0 | ± c 2 b). { displaystyle rho _ {1} = { frac {a ^ {2}} {b}} , qquad left (0 , { bigg |} , pm { frac {c ^ { 2}} {b}} right) .}
- эллипс Штейнера : эллипс, проходящий через вершины треугольника с центром в центроид,
- в эллипсах : эллипсы, соприкасающиеся со стороны треугольника. Особыми случаями являются эллипс Штейнера и эллипс Мандарта.
- Эллипсоид
- Эллиптический конус
- Эллиптический цилиндр
- Гиперболоид из одного листа
- Гиперболоид из двух листов
Эллипсоид
Эллиптический конус
Эллиптический цилиндр
Гиперболоид из одного листа
Гиперболоид из двух листов
- e = ra — rpra + rp = ra — rp 2 ara = (1 + e) arp = (1 — e) a { displaystyle { begin {align} e = { frac {r_ {a} -r_ {p}} {r_ {a} + r_ {p}}} = { frac {r_) {a} -r_ {p}} {2a}} \ r_ {a} = (1 + e) a \ r_ {p} = (1-e) a end {align}}}
- a = ra + rp 2 b = rarp ℓ = 2 1 ra + 1 rp = 2 rarpra + rp { displaystyle { begin {align} a = { frac {r_ {a} + r_) {p}} {2}} \ [2pt] b = { sqrt {r_ {a} r_ {p}}} \ [2pt] ell = { frac {2} {{ frac { 1} {r_ {a}}} + { frac {1} {r_ {p}}}}} = { frac {2r_ {a} r_ {p}} {r_ {a} + r_ {p}} } end {align}}}
.
- Из материала, который оптически анизотропный (двулучепреломляющий ), показатель преломления зависит от направления света. Зависимость может быть описана эллипсоидом индекс . (Если материал оптически изотропный, этот эллипсоид представляет собой сферу.)
- В твердотельных лазерах с лампой накачкой использовались отражатели эллиптической формы цилиндрической. для направления света от лампы накачки (коаксиально с одной фокальной осью эллипса) на стержень активной среды (коаксиально со второй фокальной осью).
- В лазерно-плазменном производстве используются источники света EUV В литографии микрочипа свет EUV генерируется плазмой, расположенной в первичном фокусе эллипсоидного зеркала, и предназначено во вторичном фокусе на представлении литографической машины.
- Рисование с использованием Безье
- Декартов овал, обобщение эллипса
- круговой и инконической
- Расстояние наибольшего сближения эллипсов
- Подгонка эллипса
- Эллиптические координаты, ортогональная система координат, основанная на семействах эллипсов и гипербол
- Эллиптических уравнение в частных производных
- Эллиптическое распределение в статистике
- Геодезические на эллипсоиде
- Большой эллипс
- Законы движения планет Кеплера
- n-эллипс, обобщение эллипса для n фокусов
- Овальный
- Сфероид, эллипсоид, полученный вращением эллипса вокруг его большой или малой оси
- Стадион (геометрия), двумерная геометрическая форма, построенная из прямоугольника с полукругами на паре противоположных сторон
- круговой эллипс Штейнера, уникальный эллипс, описывающий треугольник и d разделяет свой центроид
- Суперэллипс, обобщение эллипса, которое может выглядеть более прямоугольным или более «заостренным»
- Истинный, эксцентрический и означает аномалию
- Безант, WH (1907). «Глава III. Эллипс». Конические сечения. Лондон: Джордж Белл и сыновья. п. 50. CS1 maint: ref = harv (ссылка )
- Coxeter, HSM (1969). Введение в геометрию (2-е изд.). Нью-Йорк: Wiley. Стр. 115–9.
- Месерв, Брюс Э. (1983) [1959], Основные концепции геометрии, Дувр, ISBN 978-0-486-63415-9
- Миллер, Чарльз Д.; Лиал, Маргарет Л.; Шнайдер, Дэвид И. (1990). Основы алгебры колледжа (3-е изд.). Скотт Форесман / Литтл. Стр. 381. ISBN 978-0-673-38638-0 .
- Проттер, Мюррей Х.; Морри, Чарльз Б., младший (1970), Колледж по исчислению с аналитической геометрией (2-е изд.), Чтение: Аддисон-Уэсли, LCCN 76087042
Полярная форма относительно фокуса
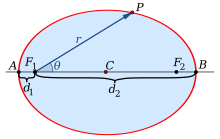
Если вместо этого мы будем использовать полярные координаты с началом в одном фокусе, с угловой координатой θ = 0 { displaystyle theta = 0}
где знак в знаменателе отрицательный, если направление ссылки θ = 0 { displaystyle theta = 0}
В немного более общем случае эллипса с одним фокусом в начале и другим фокусом в угловой координате ϕ { displaystyle phi}
Угол θ { displaystyle theta }

Эксцентриситет и свойство directrix
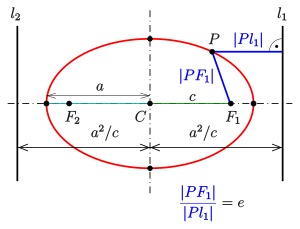
Каждая из двух линий, параллельных малой оси, и на расстоянии d = a 2 c = ae { displaystyle d = { frac {a ^ {2}} {c} } = { frac {a} {e}}}
Доказательство для пары F 1, l 1 { displaystyle F_ {1}, l_ {1}}


Второй случай доказывается аналогично.
Обратное также верно и может использоваться для определения эллипса (аналогично определению параболы):
Выбор e = 0 { displaystyle e = 0}
(выбор e = 1 { displaystyle e = 1}


Пусть F = (f, 0), e>0 { displaystyle F = (f, , 0), e>0}и предположим, что (0, 0) { displaystyle (0, , 0)}





Подстановка p = f (1 + e) { displaystyle p = f (1 + e)}
Это уравнение эллипса (e < 1 {displaystyle e<1}


Если e < 1 {displaystyle e<1}


который представляет собой уравнение эллипса с центром (a, 0) { displaystyle (a, , 0)}

Если фокус F = (f 1, f 2) { Displaystyle F = left (f_ {1}, , f_ {2} right)}

(В правой части уравнения используется нормальная форма Гессе линии для вычислений расстояния | P l | { displaystyle | Pl |}
Свойство отражения в фокусе
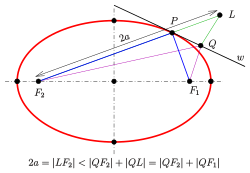
Эллипс следующим образом:
Потому что касательная перпендикулярная нормали, утверждение верно и для касательной и дополнительного угла угла между линиями к фокусам (см. Диаграмму).
Пусть L { displaystyle L}














Из диаграммы и неравенства треугольника видно, что 2 a = | L F 2 | < | Q F 2 | + | Q L | = | Q F 2 | + | Q F 1 | {displaystyle 2a=left|LF_{2}right|<left|QF_{2}right|+left|QLright|=left|QF_{2}right|+left|QF_{1}right|}



Лучи из одного фокуса отражаются эллипсом во втором положении. Это свойство имеет оптические и акустические приложения, аналогичные отражательные свойства параболы (см. шепчущая галерея ).
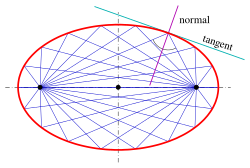
Сопряженные диаметры
Окружность имеет следующее свойство:
Аффинное преобразование параллелизм и середины. прямой сегмент, поэтому это свойство верно для любого эллипса. орды и диаметр больше не ортогональны.)
Два диаметра d 1, d 2 { displaystyle d_ {1}, , d_ {2}}

Из диаграммы можно найти:
Сопряженные диаметры в эллипсе обобщают ортогональные диаметры в окружности.
В параметрическом уравнении для общего эллипса, приведенном выше,
любая пара точек p → (t), p → (t + π) { displaystyle { vec {p}} (t), { vec { p}} (t + pi)}

Теорема Аполлония о сопряженных диаметрах

Для эллипса с полуосями a, b { displaystyle a, , b}
Пусть эллипс имеет каноническую форму с параметрическим уравнением
Две точки c → 1 = p → (т), с → 2 знака равно п → (т + π 2) { displaystyle { vec {c}} _ {1} = { vec {p}} (т), { vec {c}} _ {2 } = { vec {p}} left (t + { frac { pi} {2}} right)}

Площадь треугольника, образованная c → 1, c → 2 { displaystyle { vec {c}} _ {1}, , { vec {c}} _ {2}}
и из диаграммы видно, что площадь параллелограмма в 8 раз больше, чем у A Δ { displaystyle A _ { Delta} }
Ортогональные касательные
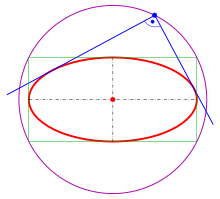
Для эллипса x 2 a 2 + y 2 b 2 = 1 { displaystyle { tfrac {x ^ {2}} {a ^ {2}}} + { tfrac {y ^ {2}} {b ^ {2}}} = 1}

Эта окружность называется ортоптической или направляющей окружностью эллипса (не путать с круговой направляющей, тип выше).
Рисование эллипсов
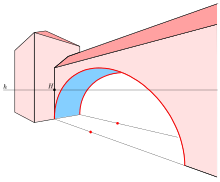
Эллипсы появляются в описательной геометрии как изображения (параллельная или центральная проекция) окружностей. Существуют различные инструменты для рисования эллипса. Компьютеры обеспечивают самый быстрый и точный метод рисования эллипса. Однако технические средства (эллипсографы ) для рисования эллипса без использования компьютера существуют. Принцип эллипсографов был известен греческим математикам, таким как Архимед и Проклос.
. Если эллипсограф недоступен, можно нарисовать эллипс, используя аппроксимацию четырьмя соприкасающимися кругами на вершины.
Для любого метода, ниже, необходимо знание осей и полуосей (или, что эквивалентно: фокусов и большой полуоси). Если это предположение не выполнено, необходимо знать как минимум два сопряженных диаметра. С помощью конструкции Ритца оси и полуоси могут быть восстановлены.
Построение точки де Ла Хира
Следующее построение отдельных точек эллипса связано с де Ла Хиром. Он основан на стандартном параметрическом представлении (a cos t, b sin t) { displaystyle (a cos t, , b sin t)}
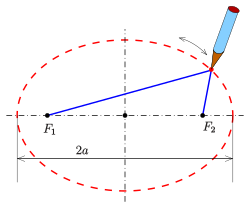
Метод булавок и цепочек
Характеристика эллипса как геометрического места точек, так что сумма расстояний до фокусов постоянна, приводит к методу рисования одного из двух булавки для рисования, веревка и карандаш. В этом методе булавки вставляются в бумагу в двух точках, которые становятся фокусами эллипса. На каждом конце к двум булавкам привязывается веревка; его длина после связывания составляет 2 a { displaystyle 2a}
Подобный метод рисования конфокальных эллипсов с замкнутой цепочкой был разработан ирландским епископом Чарльзом Грейвсом.
Методы бумажной ленты
Два следующих метода использования на параметрическом представлении (см.. параметрическое представление выше):
Технически это представление можно смоделировать двумя простыми способами. В обоих случаях центр оси и полуоси a, b { displaystyle a, , b}
Первый метод начинается с
Точка, где встречаются полуоси, отмечена P { displaystyle P}



Техническая реализация бумажной ленты может быть достигнута с помощью пары Туси (см. Анимацию). Устройство способно нарисовать любой эллипс с фиксированной суммой a + b { displaystyle a + b}
Вариант метода 1 с бумажной полоской использует наблюдение, что средняя точка N displaystyle N}







Второй метод начинается с
Одна отмечает точку, которая делит полосу на две части длиной b { displaystyle b}



Этот метод используется для нескольких эллипсографов (см. Раздел ниже).
Аналогичным способом способом 1 с бумажной полосой, можно найти вариант способа 2 с бумажной полосой (см. Диаграмму) путем разрезания части между осями пополам.
Большинство эллипсографов чертежей основы на второй метод бумажной ленты.

Аппроксимация соприкасаса разными кругами
Из метрических свойств, приведенных ниже, можно получить:
На схеме показан простой способ найти центры кривизны C 1 = (a — b 2 a, 0), С 3 знак равно (0, b — a 2 b) { displaystyle C_ {1} = left (a — { tfrac {b ^ {2}} {a}}, 0 right), , C_ {3} = left (0, b — { tfrac {a ^ {2}} {b}} right)}


(доказательство: простой расчет).
Центры остальных вершин находятся симметрично.
С помощью французской строительной кривой С помощью французской строительной кривой, которая имеет плавный контакт с соприкаса нашими кругами.
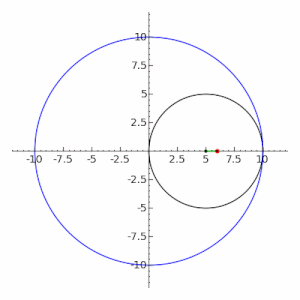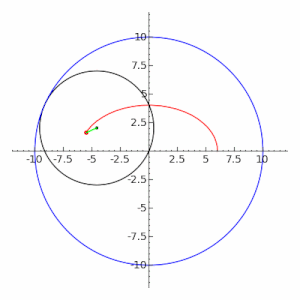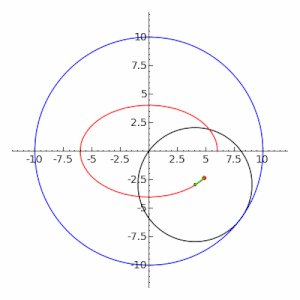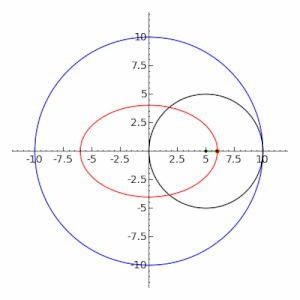
Поколение Штейнера

Следующий метод построения отдельных точек эллипса основан на генерации Штейнера конического сечения сечения :
Для генерации точек эллипс x 2 a 2 + y 2 b 2 = 1 { displaystyle { tfrac {x ^ {2}} {a ^ {2}}} + { tfrac {y ^ { 2}} {b ^ {2}}} = 1}



Р { Displaystyle P}









Генерация Штейнера также может быть определена для гипербол и парабол. Иногда его используют методом параллелограммы, потому что можно использовать другие точки, а не вершины, которые начинается с параллелограммы вместо прямоугольника.
Как гипотрохоиды
Эллипс является частным случаем гипотрохоиды , когда R = 2r, как показано на соседнем изображении. Частный случай движущегося круга с радиусом r { displaystyle r}

Вписанные углы и трехточечная форма
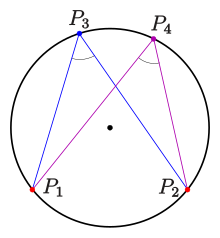
Круги
Круг с уравнением (x — x ∘) 2 + (Y — Y ∘) 2 знак равно р 2 { displaystyle left (xx _ { circ} right) ^ {2} + left (yy _ { circ} right) ^ {2} = r ^ {2}}


Обычно вписанные углы измеряются градусом или радианом θ, но здесь более удобно следующее измерение:
Теорема о вписанном угле для окружностей
Для четырех точек P i = (xi, yi), i = 1, 2, 3, 4, { displaystyle P_ {i} = left (x_ {i}, , y_ {i}) справа), i = 1, , 2, , 3, , 4, ,}
Сначала такт доступен только для хорд, не параллельных оси Y, но окончательная формула работает для любого аккорда.
Трехточечная форма уравнения круга
Например, для P 1 = (2, 0), п 2 знак равно (0, 1), п 3 знак равно (0, 0) { displaystyle P_ {1} = (2, , 0), ; P_ {2} = (0, , 1), ; P_ {3} = (0, , 0)}
Используя векторы, скалярные произведения и детерминанты, эту формулу можно упорядочить более четко, позволяя x → = (x, y) { displaystyle { vec {x} } = (x, , y)}
Центр круга (x ∘, y ∘) { displaystyle left (x _ { circ}, , y _ { circ } right)}
Радиус — это расстояние между любым из трех точек и центр.
Эллипсы
В этом разделе мы рассматриваем семейство эллипсов, определяемым уравнением (x — x ∘) 2 a 2 + (y — y ∘) 2 б 2 знак равно 1 { displaystyle { tfrac { left (xx _ { circ} right) ^ {2}} {a ^ {2}}} + { tfrac { left (yy _ { circ} right) ^ {2}} {b ^ {2}}} = 1}
и записать уравнение эллипса в виде:
где q фиксировано и x ∘, y ∘, a { displaystyle x _ { circ}, , y _ { circ}, , a}



Для этого семейства эллипсов вводится следующее q-аналог угловая мера, которая не является обычной угловой мера, которая не является обычной угловой меры θ:
Теорема о вписанном угле для эллипсов
Сначала такт доступны только для хорд, которые не параллельны оси y. Но окончательная формула работает для любого аккорда. Доказательство следует из простого вычисления. Для доказательства, что находится точка на эллипсе, можно предположить, что центр эллипса является началом координат.
Трехточечная форма уравнения эллипса
Например, для P 1 = (2, 0), P 2 = (0, 1), П 3 знак равно (0, 0) { Displaystyle P_ {1} = (2, , 0), ; P_ {2} = (0, , 1), ; P_ {3} = (0, , 0)}

Аналогично случаю круга уравнение можно записать более четко используя:
где ∗ { displaystyle *}
Отношение полюса к полюсу
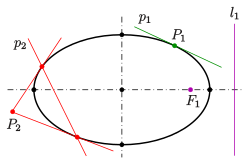
Любой эллипс можно описать в подходящей системе координат уравнением x 2 a 2 + y 2 b 2 = 1 { displaystyle { tfrac {x ^ { 2}} {a ^ {2}}} + { tfrac {y ^ {2}} {b ^ {2}}} = 1}



Это отношение между точками и линией является биекцией.
обратной функцией отображает
Такое отношение между точками и линиями, образованными коникой, называется полюсом -полярное отношение или полярность. Полюс — это точка, полярная линия.
Расчетным путем можно подтвердить следующие свойства полярно-полярного отношения эллипса:
Соотношения полюс-полярность существуют также для гипербол и парабол.
Свойства показателей
Все приведенные ниже свойства показателей относятся к эллипсу с уравнением x 2 a 2 + y 2 b 2 = 1 { displaystyle { frac {x ^ {2 }} {a ^ {2}}} + { frac {y ^ {2}} {b ^ {2}}} = 1}
Площадь
Область Эллипс { displaystyle A _ { text {ellipse}}}
где a { displaystyle a}







![{ displaystyle x in [-a, a],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fb19e5015712fa6f6c57d3f334266c73d7782434)

![[-a,a]](https://wikimedia.org/api/rest_v1/media/math/render/svg/50ccbcece37f9ec0a4c6d396be3a143a0b76d5c1)
Второй интеграл — это площадь круга радиуса a, { displaystyle a,}

Эллипс, неявно определяемый A x 2 + B xy + C y 2 = 1 { displaystyle Ax ^ {2} + Bxy + Cy ^ {2} = 1}
Площадь также может быть выражена через эксцентриситет и длину большой полуоси как a 2 π 1 — e 2 { displaystyle a ^ { 2} pi { sqrt {1-e ^ {2}}}}
Окружность
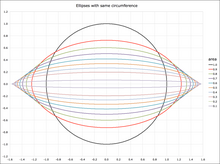
Окружность C { displaystyle C}
где снова a { displaystyle a}


, которая в общем случае не является элементарной функцией.
Окружность эллипса может быть оценена в терминах E (e) { displaystyle E (e)}
точный бесконечный ряд :
где п! ! { displaystyle n !!}

Шриниваса Рамануджан дает два близких приближения для окружности в §16 «Модульных уравнений и приближения к π { displaystyle pi}
и
Ошибки этих приближений, полученные эмпирическим путем, имеют порядок h 3 { displaystyle h ^ {3}}

В более общем смысле, длина дуги части окружности как функция от угла наклона (или x-координат любых двух точек в верхней половине эллипса), дается неполным эллиптическим интегралом . Верхняя половина эллипса параметризуется как
Тогда длина дуги s { displaystyle s}


Это эквивалентно
где E (z ∣ m) { displaystyle E (z mid m)}
Обратная функция , создающая функцию длины дуги, задается некоторой угол эллиптической функции .
Некоторая нижняя и верхняя границы окружности канонического эллипса x 2 / a 2 + y 2 / b 2 = 1 { displaystyle x ^ {2} / a ^ {2} + y ^ {2} / b ^ {2 } = 1}

Здесь верхняя граница 2 π a { displaystyle 2 pi a}

Кривизна
Кривизна определяет как κ = 1 a 2 b 2 (x 2 a 4 + y 2 b 4) — 3 2, { displaystyle kappa = { frac {1} {a ^ {2} b ^ {2}}} left ({ frac {x ^ {2}} {a ^ {4}}} + { frac {y ^) {2}} {b ^ {4}}} right) ^ {- { frac {3} {2}}} ,}

Радиус кривизны в двух вершинах (± a, 0) { displaystyle ( pm a, 0)}
Радиус кривизны в двух совпадающих вершинах (0, ± b) { displaystyle (0, pm b)}
В геометрии треугольника
Эллипсы появляются в геометрии треугольника как
В виде плоских сечений квадрик
Эллипсы появляются как плоские с использованием следующих квадрик :
Приложения
Физика
Эллиптические отражатели и акустика
Если поверхность воды нарушается в одном фокусе эллиптического резервуара с водой, Круговые волны этого возмущения после отражения от стен одновременно сходятся к одной точке: второму фокусу. Это следствие того, что общая длина пути одинакова на любом пути отскока от стен между двумя фокусами.
Аналогично, если источник света помещен в один фокус эллиптического зеркала, все световые лучи в плоскости эллипса отражаются во втором фокусе. Так как никакая другая гладкая кривая не обладает таким свойством, ее можно использовать как альтернативное определение эллипса. (В частном случае круга с кругом в центре весь свет будет отражаться обратно к центру.) Если эллипс повернуть вдоль его большой оси, чтобы получить эллипсоидальное зеркало (в частности, вытянутый сфероид ), это свойство сохраняется для всех лучей, выходящих из источника. В качестве альтернативы можно использовать цилиндрическое зеркало с эллиптическим поперечным сечением для фокусировки света от линейной люминесцентной лампы вдоль линии бумаги; такие зеркала используются в некоторых сканерах документов.
Звуковые волны отражаются аналогичным образом, поэтому в большой эллиптической комнате человек, стоящий в одном фокусе, может замечательно хорошо слышать человека, стоящего в другом фокусе. Эффект еще более очевиден под сводчатой крышей, имеющей форму вытянутого сфероида. Такая комната называется камера шепота. Тот же эффект может быть использован с двумя отражателями, расположенными между ними, расположенными сфероидами. Примеры: Национальный скульптурный зал в Капитолии США (где Джон Куинси Адамс, как говорят, использует это свойство для прослушивания вопросов); Скиния мормонов на Храмовой площади в Солт-Лейк-Сити, Юта ; на выставке звука в Музее науки и промышленности в Чикаго ; напротив Университета Иллинойса в Урбане-Шампейн Аудитория Феллингера; а также в боковой камере дворца Карла V, в Альгамбре.
планетных орбитах
В 17 веке Иоганн Кеплер обнаружил, что орбиты, по которым путешествующие вокруг Солнца, соответственно, собой эллипсы с Солнцем [приблизительно] в одном фокусе, в его первом законе движения планет. Позже Исаак Ньютон объяснил это следствие своего всемирного тяготения.
В более общем плане, в гравитационной задаче двух тел, если два тела связаны друг с другом (то есть полная энергия отрицательна), их орбиты являются подобными эллипсами, при этом общем барицентр является одним из фокусов каждого эллипса. Другой фокус любого эллипса не имеет физического физического значения. Орбита одного тела в системе отсчета другого тела также является эллипсом, а другое тело находится в том же фокусе.
Кеплеровские эллиптические орбиты являются результатом любой радиально направленной силы притяжения, сила которой обратно пропорциональна квадрату расстояния. Таким образом, в принципе двух движущихся изображений заряженных частиц. (Этот вывод игнорирует потери из-за электромагнитного излучения и квантовых эффектов, которые становятся значительными, когда частицы движутся с высокой скоростью.)
Для эллиптические орбиты, полезные соотношения, включающие эксцентриситет e { displaystyle e}
где
Кроме того, с точки зрения ra { displaystyle r_ {a}}




Гармонические осцилляторы
Общее решение для гармонического осциллятора в двух или более измерениях также является эллипсом. Так обстоит дело, например, с длинным маятником, который может свободно двигаться в двух измерениях; массы, прикрепленной к фиксированной точке с помощью идеально упругой пружины ; или любого объекта, который движется под действием силы притяжения, который прямо пропорциональна его расстоянию от фиксированного аттрактора. Однако, в отличие от кеплеровских орбитов, эти «гармонические орбиты» имеют центр притяжения в геометрическом центре эллипса и имеют довольно простые уравнения движения.
Визуализация фазы
В электронике относительную фазу двух синусоидальных сигналов можно сравнить, подав их на вертикальный и горизонтальный входы осциллографа . Если изображение фигуры Лиссажу представляет собой эллипс, а не прямую линию, два совпадения по фазе.
Эллиптические шестерни
Две некруглые шестерни с одинаковым эллиптическим контуром, каждая из которых вращается вокруг одного фокуса и установлены под нужным углом, плавно поворачиваются, сохраняя при этом контакт раз. В качестве альтернативы они могут быть соединены цепью звеньев или ремнем привода ГРМ, или, в случае велосипеда, основная передняя звезда может быть эллиптической, или яйцевидная похожая на эллипс по форме. Такие эллиптические шестерни могут быть установлены в механическом оборудовании для эксплуатации угловой или крутящего момента за счет постоянного вращения ведущей оси или, в случае велосипеда, для обеспечения вращения кривошипа. скорость с обратным изменением скорости механическое преимущество.
Эллиптические велосипедные шестерни облегчают соскальзывание цепи с зубца при переключении передач.
Пример применения шестерни может быть устройство, которое наматывает резьбу на конический шпулька на прядильной машине. Шпулька должна наматываться быстрее, когда нить находится около вершины, чем когда она находится рядом с основанием.
Оптика
Статистика и финансы
В статистике двумерный случайный вектор (X, Y) вместе эллиптически распределен, если его контуры изоплотности — равных плотности плотности функция — это эллипсы. Эта концепция произвольное количество элементов случайного вектора, и в этом случае в общем случае контуры изоплотности представит собой эллипсоиды. Особым случаем является многомерное нормальное распределение. Эллиптические распределения важны в финансах, потому что, если нормы прибыли на национальном уровне распределены эллиптически, тогда все портфели могут полностью охарактеризовать их средним значением и дисперсией портфеля, то есть любыми портфелями с одинаковыми средним средним размером и дисперсией портфеля. return имеют идентичное распределение доходности портфеля.
Компьютерная графика
Рисование эллипса в виде графического примитива распространено в стандартных библиотеках отображения, таких как MacIntosh QuickDraw API и Direct2D в Windows. Джек Брезенхэм из IBM наиболее известным изобретением примитивов 2D-рисования, включая рисование линий и окружностей, с использованием только быстрых целочисленных операций, таких как сложение и переход по биту переноса. В 1967 году MLV Pitteway расширил алгоритм Брезенхэма для линий на коники. Еще одно эффективное обобщение для рисования эллипсов было изобретено в 1984 году Джерри Ван Акеном.
В 1970 году Дэнни Коэн представил на конференции «Компьютерная графика 1970» в Англии линейный алгоритм рисования эллипсов и окружностей. В 1971 г. Л. Б. Смит опубликовал аналогичные алгоритмы для всех конических сечений и доказал их хорошие свойства. Этим алгоритмам требуется всего несколько умножений и сложений для каждого события.
В компьютерной графике полезно использовать параметрическую формулировку, потому что плотность точек максимальна там, где больше всего кривизны. Таким образом, изменение наклона между каждой точкой невелико, снижает очевидную «неровность» приближения.
Составные кривые Безье также можно использовать для рисования эллипса с достаточной точностью, поскольку любой эллипс может быть истолкован как аффинное преобразование окружности. Сплайновые методы, применяемые для рисования круга круга, преподаватели для рисования эллипса, поскольку производящие кривые Безье ведут себя соответствующим образом при таких преобразованиях.
Теория оптимизации
Иногда бывает полезно найти минимальный ограничивающий эллипс для набора точек. Метод эллипсоида весьма полезен для решения этой проблемы.
См. Также
Примечания
Ссылки
Внешние ссылки
Лекция № 3
Нормальные
сечения эллипсоида.
Вопросы лекции:
-
Нормальные сечения
эллипсоида. Радиусы кривизны в данной
точки эллипсоида. -
Расчёт рамок
съёмочных трапеций.
-
Нормальные
сечения эллипсоида. Радиусы кривизны
в данной точки эллипсоида.
Через нормаль к
поверхности эллипсоида можно провести
бесчисленное множество плоскостей. Эти
плоскости, перпендикулярные к касательной
плоскости к поверхности эллипсоида в
данной точке, называются нормальными.
Кривые, образуемые от пересечения
нормальных плоскостей, проведенных в
данной точке, с поверхностью эллипсоида
называются нормальными сечениями. В
каждой точке существуют два взаимно
перпендикулярных сечения, кривизна
которых имеет максимальное и минимальное
значения; эти нормальные сечения
называются главными
нормальными сечениями.
Г
нормальными сечениями являются
меридиональное сечение и сечение
первого вертикала. Меридиональным
сечением называется сечение, проходящее
через данную точку и оба полюса. Сечением
первого вертикала называется сечение,
проходящее через данную точку
перпендикулярно меридиональному
сечению.
Радиус кривизны
меридиана (меридионального сечения)
обозначается через М.
Радиус кривизны
первого вертикала обозначается N.
Радиус кривизны
меридиана (М)
вычисляется по формуле:.
где а
– большая полуось эллипсоида; е
– первый эксцентриситет; В
– геодезическая широта данной точки.
С увеличением
широты от В от 0 до 90º радиус кривизны
меридиана будет увеличиваться и достигнет
своего максимального значения на полюсах
при В=90º. Радиус кривизны меридианного
эллипса в полюсах называется полярным
радиусом кривизны и обозначается через
с,
тогда
П
во внимание, что или
, имеем:
Учитывая, что
можно записать:
Окончательно
имеем:
Если обозначить:
,
где
W
– первая основная функция геодезической
широты, имеем:
Приняв
где V
– вторая основная функция геодезической
широты,
и учитывая, что
и
имеем:
или
Окончательно
имеем:
Д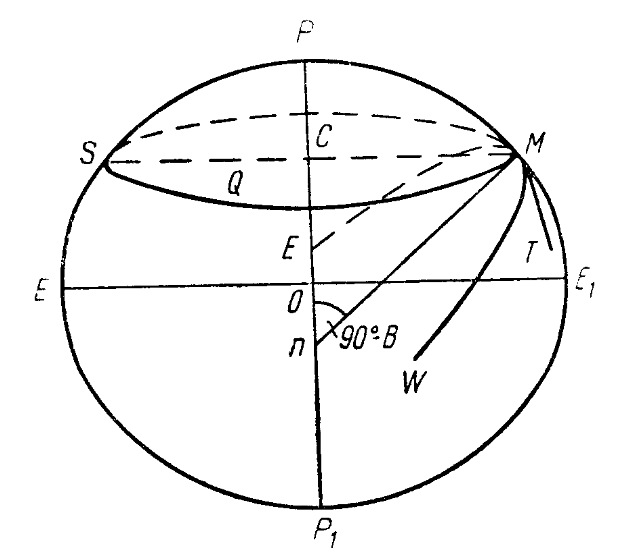
вывода радиуса кривизны первого вертикала
можно воспользоваться теоремой: если
через точку поверхности проведены два
сечения – нормальное и наклонное, причём
в рассматриваемой точке эти два сечения
имеют общую касательную, то радиус
кривизны наклонного сечения равен
радиусу нормального сечения, умноженного
на косинус угла между плоскостями этих
двух сечений:
В
данном случае наклонное сечение это
плоскость параллели, радиус которой
можно определить по формуле:
Отсюда
радиус кривизны первого вертикала (N)
вычисляется по формуле:
или
:
справедлива
также формула :
где
Средним радиусом
кривизны в данной точке называется
предел, к которому стремится среднее
арифметическое из радиусов кривизны
нормальных сечений, когда их число
стремится к бесконечности.
Средний радиус
кривизны (R)
определяется по формуле:
где М
и N
— радиусы кривизны меридиана и первого
вертикала в данной точке.
-
Расчёт рамок
съёмочных трапеций.
Р
съёмочной трапеции являются отрезки
параллелей и меридианов, поэтому расчёт
рамок съёмочных трапеций включает
определение длины дуги меридиана, длины
дуги параллели , площади съёмочной
трапеции и её диагонали.
Длина дуги
меридиана
Длина дуги (Х)
меридиана от экватора (В=00)
до точки (или до параллели) с широтой
(В)
вычисляется по формуле:
где
Для контроля длину
дуги (Х)
меридиана от экватора до точки с широтой
(В)
можно также вычислить по формуле:
г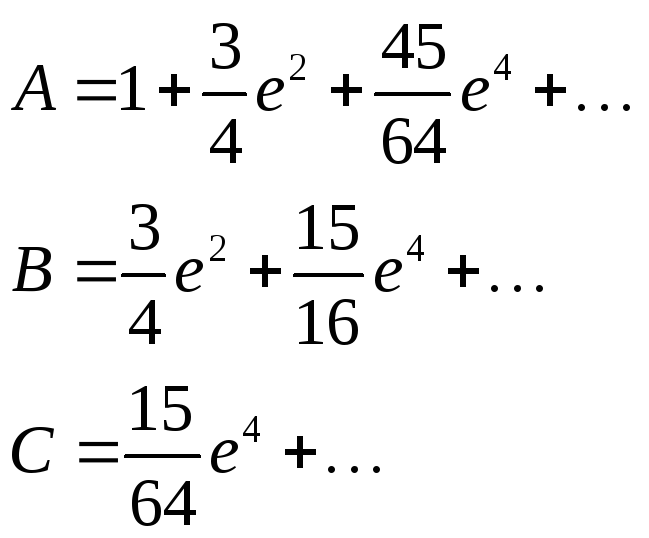
Длина дуги (ΔX)
меридиана между параллелями с широтами
В1
и В2
вычисляется по формуле:
где ΔB=В2-В1
– приращение
широты (в угловых секундах);
— средняя широта;
ρ”
= 206264,8” – количество секунд в радиане;
М1,
М2
и
Мm
– радиусы
кривизны меридиана в точках с широтами
В1,
В2
и
Вm.
Для
контроля длину дуги (ΔX)
меридиана между параллелями с широтами
В1
и В2
можно вычислить по формуле:
где Х0В1
и Х0В2
— длины дуги меридиана от экватора до
параллелей с широтами В1
и В2
Д
дуги параллели
Длина дуги параллели
вычисляется по формуле:
где N
– радиус кривизны первого вертикала в
точке с широтой В;
ΔL=L2
—
L1
– разность
долгот двух меридианов (в угловых
секундах);
ρ”
= 206264,8” – количество секунд в радиане.

сфероидической трапеции
Часть поверхности
эллипсоида, ограниченная дугами
меридианов и параллелей, является
сфероидической трапецией .
Площадь сфероидической
трапеции на поверхности эллипсоида
вычисляется по формуле:
где L1
и
L2
—
долготы западного и восточного меридианов
трапеции;
В1
и
В2
—
долготы западного и восточного меридианов
трапеции;
b
–малая полуось эллипсоида; ρ”
= 206264,8” – количество секунд в радиане;
е — первый эксцентриситет.
Вычисление
диагонали съемочной трапеции.

Диагональ съемочной
трапеции вычисляют
по формуле:
где:
d
– длина диагонали трапеции,
ΔYН
– длина
дуги параллели нижней рамки,
ΔYВ–
длина дуги параллели верхней рамки
трапеции,
ΔХ
– длина
дуги меридиана левой (правой) рамки.
Соседние файлы в папке лекции
- #
- #
- #
- #
- #
- #
- #
- #
Радиус окружности кривой линии
Рассмотрим плоскую кривую, заданную уравнением (y = fleft( x right).) Пусть в точке (Mleft( right)) проведена касательная к данной кривой, которая образует угол (alpha) с осью абсцисс (рисунок (1)). При смещении (Delta s) вдоль дуги кривой точка (M) переходит в точку (.) При этом положение касательной также изменяется: угол наклона касательной к оси (Ox) в точке () будет составлять (alpha + Deltaalpha.) Таким образом, при смещении точки кривой на расстояние (Delta s) касательная поворачивается на угол (Deltaalpha.) (Будем считать, что угол (alpha) возрастает при вращении против часовой стрелки.)
Абсолютное значение отношения (largefrac<<Delta alpha >><<Delta s>>normalsize) называется средней кривизной дуги (M.) В пределе, при (Delta s to 0,) мы получаем кривизну кривой в точке (M:) [K = limlimits_ <Delta s to 0>left| <frac<<Delta alpha >><<Delta s>>> right|.] Из приведенного определения следует, что кривизна в какой-либо точке кривой характеризует скорость вращения касательной в этой точке.
Для плоской кривой (y = fleft( x right)) кривизна в точке (Mleft( right)) выражается через первую и вторую производные функции (fleft( x right)) по формуле [K = frac <<left| right|>> <<<<left[ <1 + <<left( right)>^2>> right]>^<largefrac<3><2>normalsize>>>>.] Если кривая задана в параметрической форме уравнениями (x = xleft( t right),) (y = yleft( t right),) то ее кривизна в произвольной точке (Mleft( right)) равна [K = frac <<left| right|>> <<<<left[ <<<left( right)>^2> + <<left( right)>^2>> right]>^<largefrac<3><2>normalsize>>>>.] В случае, если кривая задана полярным уравнением (r = rleft( theta right),) кривизна находится по формуле [K = frac <<left| <+ 2 <<left( right)>^2> — rr»> right|>> <<<<left[ <+ <<left( right)>^2>> right]>^<largefrac<3><2>normalsize>>>>.] Радиусом кривизны кривой в точке (Mleft( right)) называется величина, обратная кривизне (K) данной кривой в рассматриваемой точке: [R = frac<1>.] Следовательно, для плоских кривых, заданных явным уравнением (y = fleft( x right),) радиус кривизны в точке (Mleft( right)) будет определяться выражением [R = frac <<<<left[ <1 + <<left( right)>^2>> right]>^<largefrac<3><2>normalsize>>>> <<left| right|>>.]
Очевидно, достаточно найти кривизну эллипса в точках (Aleft( right)) и (Bleft( <0,b>right)) (рисунок (2)), поскольку в силу симметрии кривой кривизна в двух противоположных вершинах эллипса будет такой же.
Для расчета кривизны удобно перейти от канонического уравнения эллипса к уравнению в параметрической форме : [x = acos t,;;;y = bsin t.] где (t) − параметр. В точке (Aleft( right)) параметр имеет значение (t = 0,) а в точке (Bleft( <0,b>right)) его значение равно (t = largefrac<pi ><2>normalsize.)
Данная функция достигает максимума в точках (x = largefrac<<2pi n>>normalsize,;n in Z.) В силу периодичности кривизна во всех точках максимума одинакова, поэтому достаточно рассмотреть лишь точку (x = 0).
В данном случае точка (x = 0) является точкой перегиба функции (y = arctan x.) Поскольку в точке перегиба вторая производная равна нулю, то кривизна здесь также должна быть равна нулю, что и показывает полученное решение.
Экспоненциальная функция (y = ) − это единственная уникальная функция, у которой производные любого порядка равны самой функции. Поэтому для кривизны данной кривой можно сразу написать следующую формулу: [ right|>> <<<<left[ <1 + <<left( right)>^2>> right]>^<largefrac<3><2>normalsize>>>> > = <frac<<>><<<<left( <1 + >> right)>^<largefrac<3><2>normalsize>>>>.> ] Знак модуля в числителе опущен, поскольку экспоненциальная функция всегда положительна.
Радиус кривизны плоской кривой
Любая линия является кривой, даже прямая. Поэтому к любой линии применимы такие характеристики как кривизна или радиус кривизны. Как правило кривизна обозначается латинской литерой k, а радиус кривизны греческой литерой ρ.
Между собой эти характеристики кривой связаны следующим образом:
k = 1/ρ (542.1)
Т.е. чем больше радиус кривой, тем меньше ее кривизна.
А теперь рассмотрим несколько частных случаев кривых.
Радиус кривизны окружности
Окружность — это плоская кривая с постоянным радиусом кривизны. Т.е. радиус окружности это и есть радиус кривизны окружности:
Как определить радиус окружности, мы рассмотрим ниже.
Кривизна дуги
Любая дуга — это часть окружности. Соответственно радиус дуги равен радиусу окружности:
Рисунок 542.1. Дуга — часть окружности
На рисунке 542.1 мы видим дугу АВ, показанную оранжевым цветом, являющуюся частью окружности с радиусом R. Кроме того, мы видим, что угол α, образованный радиусами в точках А и В, равен углу между касательными (показаны фиолетовым цветом) к окружности в этих точках.
Эти закономерности позволяют определить радиус дуги и найти центр окружности даже тогда, когда изначально мы окружность не видим, а только имеем дугу.
Понятие кривизны дуги формулируется так:
Кривизна дуги — это отношение угла между касательными, проведенными в начале и конце дуги, к длине дуги
Т.е. зная длину дуги m и угол α между касательными, мы можем определить кривизну дуги:
А так как длина дуги зависит от угла между радиусами или между касательными в концах дуги:
то, подставив значение длины дуги в уравнение (542.3), получим:
Примечание: При измерении угла между касательными не в радианах, а в градусах уравнение длины дуги имеет другой вид:
но сути дела это не меняет. Такая запись по-прежнему означает, что мы рассматриваем часть длины окружности. Так при α = 360° дуга становится окружностью
Более того, сама идея радианов на этой формуле и основана, так прямой угол 90° = П/2, развернутый 180° = П и т.д.
И еще одно интересное свойство дуги: Если соединить точки А и В прямой линией, то угол между этой линией и касательными будет равен α/2, а сама прямая линия — это и есть расстояние между точками А и В. Если дуга расположена в плоскости соответствующим образом, например так, как показано на рисунке 542.2:
Рисунок 542.2. Дуга из точки начала координат.
то расстояние между точками — это проекция l дуги на ось х. А максимальное расстояние между дугой и осью х — это стрела дуги h.
Радиус кривизны прямой линии
Любая прямая линия, даже бесконечно длинная, может рассматриваться как бесконечно малая часть окружности, т.е. как дуга. Соответственно в каких единицах измерять радиус такой окружности даже трудно представить.
Поэтому обычно прямой линией называют кривую с бесконечно большим радиусом:
kп.л = 1/∞ = 0 (542.6)
Про до сих пор неразрешенный парадокс, возникающий при подобных подходах к прямой линии и к окружности, я уже упоминал в статье «Основы геометрии. Определения основных элементов, пятый элемент». Здесь лишь добавлю, что через прямую линию можно провести бесконечное множество плоскостей и в любой из этих плоскостей радиус кривизны прямой линии будет равен бесконечности. При этом через окружность можно провести две взаимно перпендикулярные плоскости, в одной из которых окружность будет окружностью, а в другой — прямой линией конечной длины. Поэтому
все линии, которые в одной из плоскостей имеют бесконечно большой радиус кривизны, считаются плоскими
Ну и на закуску еще несколько парадоксов, на этот раз связанных с определениями кривизны и радиуса:
1. Из уравнения (542.1) можно сделать вывод, что:
kp = 1 (542.7)
Соответственно для прямой линии:
0·∞ = 1 (542.7.2)
Т.е. если бесконечно много раз взять ноль, то на единичку мы наскребем. Впрочем дальше будет еще веселее.
2. Если прямая — это дуга с бесконечно большим радиусом, соответственно касательные, проведенные в концах такой дуги, совпадают с прямой, а угол, образованный касательными, равен нулю.
Это означает, что радиусы проведенные в концах дуги — прямой линии, являются параллельными прямыми и не могут пересекаться. А между тем по определению это радиусы, которые обязательно должны сходиться в некоторой точке — центре окружности.
Получается, что параллельные прямые пересекаться не должны, но где-то в бесконечности все-таки пересекаются.
Разрешить этот парадокс пытались многие математики, однако в пределах евклидовой геометрии при принятом толковании определений данный парадокс не разрешим.
Радиус кривизны точки
Точка — это самый простой и самый сложный элемент геометрии. Одни считают, что точка не имеет размеров, а значит и определить кривизну или радиус кривизны точки не возможно. Другие, в частности Евклид, считают, что точка не имеет частей, а каковы при этом размеры точки — не совсем понятно. Я же считаю, что точка — это начальный, далее не делимый элемент геометрии, размеры которого пренебрежимо малы по сравнению с остальными рассматриваемыми элементами. В этом случае для точки будут справедливыми следующие уравнения кривизны и радиуса кривизны:
kт. = 1/0 = ∞ (542.9)
И хотя нас с первых лет обучения в школе учат, что делить на 0 нельзя и даже встроенный в операционную систему калькулятор пишет, что «деление на ноль невозможно», тем не менее делить на ноль можно, а результатом деления всегда будет бесконечность.
Как и в случае с прямой мы имеем парадоксальный результат, выражаемый формулой (542.5.2). Тем не менее точку также можно отнести к плоской кривой, имеющей постоянный радиус кривизны.
Примечание: На мой взгляд большинство из описанных выше парадоксов возникают из-за неправильного толкования понятия «бесконечность». Бесконечность как некая абсолютная величина не имеет пределов, а значит и никакому измерению не поддается. Кроме того бесконечность — это даже не постоянная, а переменная величина. Например луч — это прямая линия с началом в некоторой точке. Длина луча может быть бесконечно большой. При этом прямая линия тоже может быть бесконечно длинной при этом не иметь ни начала ни конца. Получается, что с одной стороны бесконечно длинный луч вроде бы в 2 раза короче, чем бесконечно длинная прямая. А с другой стороны длины их бесконечны и поэтому равны.
Возможным выходом из этой ситуации является принятие понятия «бесконечность», как относительного. Например, кривизна прямой линии является пренебрежимо малой величиной по отношению к радиусу кривизны. Или радиус кривизны прямой линии несопоставимо больше кривизны. Подобные толкования допускают и наличие кривизны прямой и некое конечное значение радиуса кривизны прямой и многое другое. Я бы назвал такой относительный подход к рассмотрению проблемы реалистичным, а подходы, использующие абсолютные понятия — идеализированными. Впрочем прямого отношения к теме данной статьи это не имеет. Продолжим рассмотрение плоских кривых.
И окружность и прямая линия являются плоскими кривыми с постоянным радиусом кривизны. При этом радиус кривизны прямой линии всегда известен, так как равен бесконечности, а для окружности всегда можно определить радиус, воспользовавшись теоремой Пифагора. Так в частном случае, если центр окружности совпадает с началом координат рассматриваемой плоскости (u = 0; v = 0 — координаты центра окружности), то:
Рисунок 541.4. Радиус окружности, как гипотенуза прямоугольного треугольника.
R 2 = x 2 + y 2 (541.1.2)
А в общем случае, когда координаты центра окружности не совпадают с началом координат:
Рисунок 542.3. Окружность, центр которой не совпадает с началом координат.
R 2 = (x — u) 2 + (y — v) 2 (542.10)
Но в жизни достаточно часто приходится сталкиваться с кривыми, радиус кривизны которых — не постоянная величина. Более того, этот радиус может изменяться в двух плоскостях измерения. Тем не менее так далеко углубляться в геометрию и алгебру мы не будем и далее рассмотрим, как можно определить радиус плоской кривой в некоторой точке.
Плоские кривые с изменяющимся радиусом кривизны
Примеров плоских кривых с изменяющимся радиусом кривизны очень много, это и гиперболы, и параболы, и синусоиды и т.п. Определение радиуса кривизны таких кривых основано на следующих теоретических предпосылках:
1. Любую окружность можно рассматривать как некоторое множество дуг.
2. Если количество дуг, составляющих окружность, стремится к бесконечности, то соответственно длина таких дуг стремится к нулю (m → 0).
3. Если мы обозначим длину такой очень короткой дуги как приращение функции длины окружности (m = Δl), то уравнение кривизны (542.3) примет следующий вид:
(542.3.1)
4. Тогда любую плоскую кривую с изменяющимся радиусом можно рассматривать как стремящееся к бесконечности множество дуг с постоянным радиусом. Другими словами в пределах любой кривой, описываемой параметрическими уравнениями, всегда можно выделить дугу, пусть даже и очень малой длины, стремящейся к точке и определить для нее кривизну и радиус кривизны в рассматриваемой точке.
Это означает, что самый точный способ определения радиуса кривизны в таком случае — это использование дифференциальных исчислений. В общем случае для этого нужно два раза продифференцировать уравнение радиуса окружности (542.10) по аргументу функции х, а затем извлечь квадратный корень из полученного результата. В итоге (полный вывод уравнения здесь не привожу из-за повышенной сложности записи, а для особо заинтересованных есть справочники и другие сайты) мы получим следующую формулу для определения радиуса кривизны:
(542.11)
Соответственно кривизна плоской кривой в рассматриваемой точке будет равна:
(542.12)
В частном случае, когда тангенс угла между касательными — первая производная от функции — является относительно малой величиной, например, tg2° = 0.035 соответственно (tg2°) 2 = 0.0012, то влиянием куба суммы первой производной и единицы на кривизну можно пренебречь (значение знаменателя дроби сводится к единице) и тогда:
k = y» = d 2 y/dx 2 (542.12.2)
Т.е. формально в таких случаях кривизной считается не отношение угла наклона между касательными к длине дуги, а некоторая величина, примерно соответствующая высоте h на рисунке 542.2.
Эта особенность второй производной очень активно используется в частности для упрощения определения прогиба элементов строительных конструкций.
На этом пока все.
Доступ к полной версии этой статьи и всех остальных статей на данном сайте стоит всего 30 рублей. После успешного завершения перевода откроется страница с благодарностью, адресом электронной почты и продолжением статьи. Если вы хотите задать вопрос по расчету конструкций, пожалуйста, воспользуйтесь этим адресом. Зараннее большое спасибо.)). Если страница не открылась, то скорее всего вы осуществили перевод с другого Яндекс-кошелька, но в любом случае волноваться не надо. Главное, при оформлении перевода точно указать свой e-mail и я обязательно с вами свяжусь. К тому же вы всегда можете добавить свой комментарий. Больше подробностей в статье «Записаться на прием к доктору»
Для терминалов номер Яндекс Кошелька 410012390761783
Номер карты Ymoney 4048 4150 0452 9638 SERGEI GUTOV
Для Украины — номер гривневой карты (Приватбанк) 5168 7422 4128 9630
Категории:
- Расчет конструкций . Основы прикладной геометрии
Оценка пользователей:
10.0 (голосов: 1)
Переходов на сайт:
6701
Комментарии:
Примечание: Возможно ваш вопрос, особенно если он касается расчета конструкций, так и не появится в общем списке или останется без ответа, даже если вы задатите его 20 раз подряд. Почему, достаточно подробно объясняется в статье «Записаться на прием к доктору» (ссылка в шапке сайта).
Радиус, круг и центр кривизны
Вы будете перенаправлены на Автор24
Смысл понятий радиуса, круга и центра кривизны
В технических приложениях часто оказывается удобным использовать окружности для приближенной замены кривой в окрестностях рассматриваемых точек. Это существенно упрощает решение целого ряда задач за счет применения более удобных выражений.
Наиболее употребительными характеристиками любой кривой являются касательная и нормаль. Касательная — предельное положение секущей $MN$ при неограниченном приближении точки $N$ к точке $M$ вдоль кривой. Нормаль — прямая, проходящая через точку касания перпендикулярно касательной.
Уравнение касательной в точке $Mleft(x_ <0>,y_ <0>right)$ к кривой $y=fleft(xright)$ имет вид $y-y_ <0>=y’left(x_ <0>right)cdot left(x-x_ <0>right)$, уравнение нормали $y-y_ <0>=-frac<1> right)> cdot left(x-x_ <0>right)$.
Записать уравнения касательной и нормали к кривой $y=3cdot x^ <2>-x+2$ в заданной точке $x_ <0>=1$.
Значение функции в заданной точке: $y_ <0>=yleft(x_ <0>right)=yleft(1right)=3cdot 1^ <2>-1+2=4$.
Значение производной в заданной точке:
[y’=left(3cdot x^ <2>-x+2right)^ <<‘>> =6cdot x-1; y’left(x_ <0>right)=y’left(1right)=6cdot 1-1=5.]
Уравнение касательной: $y-4=5cdot left(x-1right)$ или $5cdot x-y-1=0$.
Уравнение нормали: $y-4=-frac<1> <5>cdot left(x-1right)$ или $x+5cdot y-21=0$.
Радиус кривизны — это параметр кривой, значение которого обратно значению кривизны $R=frac<1> $. Следовательно, это такая же переменная величина, как и кривизна.
Если в данной точке $M$ построить нормаль к кривой и отложить на ней в сторону вогнутости кривой отрезок, равный по длине радиусу кривизны кривой в этой точке, то получим точку — центр кривизны. Окружность с центром в полученной точке и радиусом, равным радиусу кривизны — это круг кривизны. Так как данная кривая и её круг кривизны касаются в данной точке, то они имеют в данной точке общую касательную. Кроме того, значения кривизны кривой и круга кривизны в данной точке совпадают.
Важным свойством круга кривизны является то, что он является соприкасающимся кругом, то есть предельным положением круга, проходящего через три точки кривой, стремящимся к совпадению в данной.
Если некоторая точка перемещается вдоль кривой, то и соответствующий ей центр кривизны также описывает некоторую кривую. Геометрическое место центров кривизны данной кривой называется её эволютой. При этом данная кривая по отношению к своей эволюте называется её эвольвентой.
Вычисление радиуса и определение центра круга кривизны
Формулы для радиуса кривизны получить легко, если известны формулы для вычисления кривизны кривой.
При произвольном параметрическом задании кривой $x=xleft(tright)$ и $y=yleft(tright)$ имеем $R=frac <sqrt<left(left(x’_right)^ <2>+left(y’_ right)^ <2>right)^ <3>> > cdot x’_ -x»_ cdot y’_ > $.
Если кривая задана в явном виде $y=fleft(xright)$, то $R=frac <sqrt<left(1+left(y’right)^<2>right)^ <3>> > $.
Если кривая задана в полярных координатах $rho =rho left(phi right)$, то $R=frac <sqrt<left(rho ^<2>+left(rho ‘_ <phi >right)^ <2>right)^ <3>> > <rho ^<2>+2cdot left(rho ‘_ <phi >right)^ <2>-rho cdot rho »_ <phi phi >> $.
Готовые работы на аналогичную тему
Найти радиус кривизны экспоненты $y=e^ $ при $x=0$.
Находим производные: $y’=e^ $; $y»=e^ $.
По формуле для радиуса кривизны получаем:
Вычисляем радиус кривизны экспоненты при $x=0$:
Найти радиус кривизны кардиоиды $rho =1+cos phi $.
Находим производные: $rho ‘=-sin phi $; $rho »=-cos phi $.
[rho ^ <2>+rho ‘^ <2>=left(1+cos phi right)^ <2>+left(-sin phi right)^ <2>=2cdot left(1+cos phi right);] [rho ^ <2>+2cdot rho ‘^ <2>-rho cdot rho »=left(1+cos phi right)^ <2>+2cdot left(-sin phi right)^ <2>-left(1+cos phi right)cdot left(-cos phi right)=] [=3cdot left(1+cos phi right).]
По формуле для радиуса кривизны получаем:
Найдем координаты центра кривизны $Pleft(x_ ;y_ right)$ кривой $y=fleft(xright)$.
Координаты центра кривизны для точки $Mleft(x;yright)$ удовлетворяют уравнению нормали $y_ -y=-frac<1> cdot left(x_ -xright)$.
Уравнение круга кривизны: $left(x-x_ right)^ <2>+left(y-y_ right)^ <2>=R^ <2>$.
Координаты центра кривизны по существу являются параметрическими уравнения эволюты.
Найти эволюту параболы $y=x^ <2>$. Результаты представить графически.
Находим производные: $y’=2cdot x$; $y»=2$.
По формулам $left<begin =x-frac right)> > \ =y+frac <1+y’^<2>> > endright. $ находим координаты центра кривизны для произвольной точки $Mleft(x;yright)$.
Полученные выражения фактически представляют собой параметрические уравнения эволюты, в которых $x$ является параметром. Если исключить параметр $x$ из этих уравнений, то может быть получено уравнение вида $Fleft(x_ ;y_ right)=0$, которое непосредственно связывает координаты эволюты.
Совмещенный график эвольвенты $y=x^ <2>$ и её эволюты:
На графике синей линией изображена парабола $y=x^ <2>$, а красной линией — её эволюта. Эволюта представляет собой полукубическую параболу.
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 30 11 2022
http://doctorlom.com/item542.html
http://spravochnick.ru/matematika/krivizna_krivoy/radius_krug_i_centr_krivizny/
Радиус — кривизна — эллипс
Cтраница 1
Радиус кривизны эллипса рэ при зацеплении зубьев в полюсе рэ a / b d / ( 2 cos2 P) одновременно представляет собой радиус делительной окружности эквивалентного прямозубого цилиндрического колеса.
[1]
Теперь нужно найти радиус кривизны эллипса в точке А.
[2]
Окружность 2 — крайняя правая; радиус ее является радиусом кривизны огибающего эллипса в точке / 2, а вершина располагается в крайней правой точке ( точка С) участка ABC вспомогательного эллипса. Окружность 3 — средняя окружность, она имеет наибольший радиус и касается огибающего эллипса в наивысшей его точке — точке В, а вершина этой окружности располагается в наивысшей точке ( точка В) участка ABC вспомогательного эллипса. Наконец, окружность 4 — это окружность общего положения ( текущая окружность рассматриваемого семейства), она касается огибающего эллипса в точке М и имеет вершину в точке N, лежащей на участке ABC вспомогательного эллипса. Окружности общего расположения всплошную заполняют заштрихованную на рис. 5.32, г область. Каждой точке участка ABC вспомогательного эллипса соответствует определенное значение коэффициента иа, а следовательно, и определенный тип напряженного состояния. Точки F, и F % — точки пересечения вспомогательного эллипса с осью абсцисс — являются фокусами огибающего эллипса.
[3]
Для определения условий зацепления шевера и колеса заменяем действительный шевер условным, с радиусом, равным радиусу кривизны эллипса в точке малой полуоси. Радиус условного шевера Qycjl определяем по приведенной формуле. Аналогично пересчитываем радиусы условных начальных окружностей нового и переточенного шевера.
[4]
Для определения условий зацепления шевера и колеса заменяем действительный шевер условным, с радиусом, равным радиусу кривизны эллипса в точке малой полуоси. Радиус условного шевера дусл определяем по приведенной формуле. Аналогично пересчитываем радиусы условных начальных окружностей нового и переточенного шевера.
[5]
Приведенное число зубьев zt есть то число зубьев, которое имеет фреза с радиусом Rt, соответствующим радиусу кривизны эллипса в направлении малой его оси.
[6]
Приведенное число зубьев z — t есть то число зубьев, которое имеет фреза с радиусом R [ t соответствующим радиусу кривизны эллипса в направлении малой его оси.
[7]
На рис. 5.32, в изображены оба эллипса и четыре окружности Мора из бесконечного множества окружностей семейства, соответствующего выбранной комбинации оокт и токт. Окружность / — крайняя левая; радиус ее является радиусом кривизны огибающего эллипса в точке / Сь а вершина располагается в крайней левой точке ( точка А) участка ABC вспомогательного эллипса.
[8]
Геометрическое истолкование этого наблюдения такое: функция / имеет в точке t0 особенность A i, если и только если нормаль к эллипсу, восстановленная в точке у ( f0), проходит через точку ( 1 / 2, 0), и особенность Л2, если и только если точка ( 1 / 2, 0) является центром кривизны эллипса в точке v ( A) ( ср. На рис. 3.1 изображен образ кривой б для двух значений Ь, а именно b 1 / 2 и. Учитывая, что радиус кривизны эллипса в точках ( 1, 0) и ( — 1, 0) равен Ь2 ( см. упр.
[10]
Исключение составляют, разумеется, те точки, где радиус кривизны имеет экстремальное значение. Так, вблизи вершины О, где радиус кривизны параболы имеет минимальное значение, парабола целиком лежит вне круга кривизны Ct. Напротив, вблизи вершины В, где радиус кривизны эллипса имеет максимальное значение, эллипс ( см. рис. 180) располагается целиком внутри соответствующего круга кривизны С.
[11]
Страницы:
1




















 .
. называется фокусами и расстояние 2 a { displaystyle 2a}
называется фокусами и расстояние 2 a { displaystyle 2a} равно 2 a { displaystyle 2a}
равно 2 a { displaystyle 2a}
 :
:

 ,
, .
.



 ,
,

 с s ∈ R. { displaystyle s in mathbb {R} .}
с s ∈ R. { displaystyle s in mathbb {R} .}

 Затем строка g { displaystyle g}
Затем строка g { displaystyle g} , поэтому касательная линия имеет уравнение x 1 a 2 x + y 1 б 2 y = к { textstyle { frac {x_ {1}} {a ^ {2}}} x + { tfrac {y_ {1}} {b ^ {2}}} y = k}
, поэтому касательная линия имеет уравнение x 1 a 2 x + y 1 б 2 y = к { textstyle { frac {x_ {1}} {a ^ {2}}} x + { tfrac {y_ {1}} {b ^ {2}}} y = k} для некоторых k { displaystyle k}
для некоторых k { displaystyle k} . <Времен738>(x 1, y 1) { displaystyle (x_ {1}, , y_ {1})}
. <Времен738>(x 1, y 1) { displaystyle (x_ {1}, , y_ {1})} .
. Тогда строка g { displaystyle g}
Тогда строка g { displaystyle g}





![{displaystyle {begin{aligned}a,b={frac {-{sqrt {2{Big (}AE^{2}+CD^{2}-BDE+(B^{2}-4AC)F{Big)}left((A+C)pm {sqrt {(A-C)^{2}+B^{2}}}right)}}}{B^{2}-4AC}}\x_{circ }={frac {2CD-BE}{B^{2}-4AC}}\[3pt]y_{circ }={frac {2AE-BD}{B^{2}-4AC}}\[3pt]theta ={begin{cases}arctan left({frac {1}{B}}left(C-A-{sqrt {(A-C)^{2}+B^{2}}}right)right){text{for }}Bneq 0\0{text{for }}B=0, A<C\90^{circ }{text{for }}B=0, A>C \ end {case}} end {align}}}](https://ru.wikibrief.org/wiki/%20//wikimedia.org/api/rest_v1/media/math/render/svg/acde65bb036f1c47ad935258399a696f50875a68)








 .
.



 .
. быть векторми в дизайне.
быть векторми в дизайне.
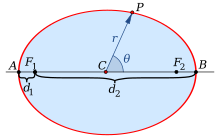 Полярные координаты с центром в центре.
Полярные координаты с центром в центре. 




 (фокус), любая строка l { displaystyle l}
(фокус), любая строка l { displaystyle l} эллипс — это геометрическое место точек, для которых отношение расстояний до точки и линии равно e, { displaystyle e, }
эллипс — это геометрическое место точек, для которых отношение расстояний до точки и линии равно e, { displaystyle e, } то есть:
то есть:

 и x 2 (e 2-1) + 2 xf (1 + e) - y 2 = 0. { displaystyle x ^ {2} left (e ^ {2} -1 right) + 2xf (1 + e) -y ^ {2} = 0.}
и x 2 (e 2-1) + 2 xf (1 + e) - y 2 = 0. { displaystyle x ^ {2} left (e ^ {2} -1 right) + 2xf (1 + e) -y ^ {2} = 0.}




 эллипса сопряжены, если касательные в точке P 1 { displaystyle P_ {1}}
эллипса сопряжены, если касательные в точке P 1 { displaystyle P_ {1}} и Q 1 { displaystyle Q_ { 1}}
и Q 1 { displaystyle Q_ { 1}} параллельны P 2 Q 2 ¯ { displaystyle { overline {P_ {2} Q_ {2}}}}
параллельны P 2 Q 2 ¯ { displaystyle { overline {P_ {2} Q_ {2}}}} .
.
 и c 2 { displaystyle c_ {2}}
и c 2 { displaystyle c_ {2}} ,
, , имеет постоянную площадь A Δ = 1 2 ab { textstyle A _ { Delta} = { frac {1} {2}} ab}
, имеет постоянную площадь A Δ = 1 2 ab { textstyle A _ { Delta} = { frac {1} {2}} ab}

 .
.

 и осями эллипса.
и осями эллипса. соответственно..
соответственно..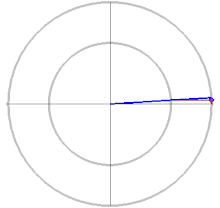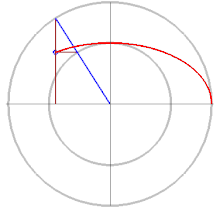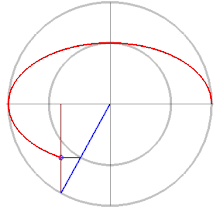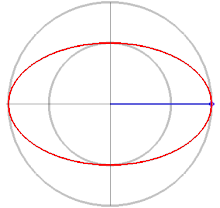


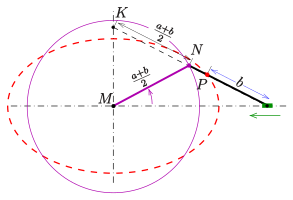

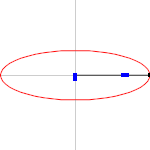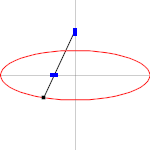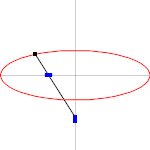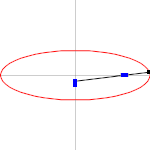

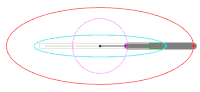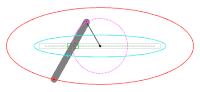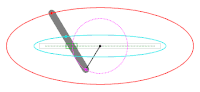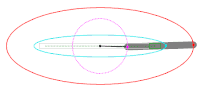
 и нарисуйте отрезок линии V 1 V 3, { displaystyle V_ {1} V_ {3} ,}
и нарисуйте отрезок линии V 1 V 3, { displaystyle V_ {1} V_ {3} ,}
 , которая перпендикулярна линии V 1 V 3, { displaystyle V_ {1} V_ {3} ,}
, которая перпендикулярна линии V 1 V 3, { displaystyle V_ {1} V_ {3} ,} линий в двух точках U, V { displaystyle U, , V}
линий в двух точках U, V { displaystyle U, , V} (все строки, содержащие U displaystyle U}
(все строки, содержащие U displaystyle U} и V { displaystyle V}
и V { displaystyle V} соответственно) и проекционное, но не перспективное отображение π { displaystyle pi}
соответственно) и проекционное, но не перспективное отображение π { displaystyle pi} на B (V) { displaystyle B (V)}
на B (V) { displaystyle B (V)} , то точки пересечения соответствующих прямых образуют невырожденное проективное коническое сечение.
, то точки пересечения соответствующих прямых образуют невырожденное проективное коническое сечение. и P 4 { displaystyle P_ {4}}
и P 4 { displaystyle P_ {4}} равны.
равны. используется частное:
используется частное:


 :
:

 , который можно переформатировать в (x — 1) 2 + (y — 1 2) 2 = 5 4. { displaystyle (x-1) ^ {2} + left (y — { tfrac {1} {2}} right) ^ {2} = { tfrac {5} {4}} .}
, который можно переформатировать в (x — 1) 2 + (y — 1 2) 2 = 5 4. { displaystyle (x-1) ^ {2} + left (y — { tfrac {1} {2}} right) ^ {2} = { tfrac {5} {4}} .}





 используется частное:
используется частное:

 , три из них на прямой (см. диаграмму).
, три из них на прямой (см. диаграмму). тогда и только тогда, когда углы в P 3 { displaystyle P_ {3}}
тогда и только тогда, когда углы в P 3 { displaystyle P_ {3}}

 и после преобразования (x — 1) 2 2 + (y — 1 2) 2 1 2 = 1. { displaystyle { frac {(x-1) ^ {2}} {2}} + { frac { left (y — { frac {1} {2}} right) ^ {2}} { frac {1} { 2}}} = 1.}
и после преобразования (x — 1) 2 2 + (y — 1 2) 2 1 2 = 1. { displaystyle { frac {(x-1) ^ {2}} {2}} + { frac { left (y — { frac {1} {2}} right) ^ {2}} { frac {1} { 2}}} = 1.}


 отображается в строке x 1 xa 2 + y 1 yb 2 = 1 { displaystyle { tfrac {x_ {1} x} {a ^ {2}}} + { tfrac {y_ {1} y} {b ^ {2}}} = 1}
отображается в строке x 1 xa 2 + y 1 yb 2 = 1 { displaystyle { tfrac {x_ {1} x} {a ^ {2}}} + { tfrac {y_ {1} y} {b ^ {2}}} = 1} , а не через центр эллипса.
, а не через центр эллипса. на точку (- ma 2 d, б 2 d) { displaystyle left (- { tfrac {ma ^ {2}} {d}}, , { tfrac {b ^ {2}} {d}} справа)}
на точку (- ma 2 d, б 2 d) { displaystyle left (- { tfrac {ma ^ {2}} {d}}, , { tfrac {b ^ {2}} {d}} справа)} и
и на точку (а 2 с, 0). { displaystyle left ({ tfrac {a ^ {2}} {c}}, , 0 right) .}
на точку (а 2 с, 0). { displaystyle left ({ tfrac {a ^ {2}} {c}}, , 0 right) .}
 ).
). ).
). ).
). и (- c, 0) { displaystyle (-c, , 0)}
и (- c, 0) { displaystyle (-c, , 0)} соответственно и директрисы x = a 2 c { displaystyle x = { tfrac {a ^ {2}} {c}}}
соответственно и директрисы x = a 2 c { displaystyle x = { tfrac {a ^ {2}} {c}}} и x = — a 2 c { displaystyle x = — { tfrac {a ^ {2}} {c}}}
и x = — a 2 c { displaystyle x = — { tfrac {a ^ {2}} {c}}} соответственно относятся к парам полюса и полюса.
соответственно относятся к парам полюса и полюса.





![{ displaystyle { begin {align} C = 2 pi a left [{1- left ({ frac {1} {2}} right) ^ {2} e ^ {2} - left ({ frac {1 cdot 3 } {2 cdot 4}} right) ^ {2} { frac {e ^ {4}} {3}} - left ({ frac {1 cdot 3 cdot 5} {2 cdot 4 cdot 6}} right) ^ {2} { frac {e ^ {6}} {5}} - cdots} right] \ = 2 pi a left [1- sum _ {n = 1} ^ { infty} left ({ frac {(2n -1) !!} {(2n) !!}} right) ^ {2} { frac {e ^ {2n}} {2n-1}} right] \ = - 2 pi a sum _ {n = 0} ^ { infty} left ({ frac {(2n-1) !!} {(2n) !!}} right) ^ {2} { frac {e ^ {2n }} {2n-1}}, end {align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3e202a234c19a28620ecf9c6d260eb21b1bd7aa0)
![{ displaystyle { begin {align} C = pi (a + b) sum _ {n = 0} ^ { infty} left ({ frac {(2n-3) !!} {2 ^ {n} n!}} right) ^ {2} h ^ {n} \ = pi (a + b) left [ 1 + { frac {h} {4}} + sum _ {n = 2} ^ { infty} left ({ frac {(2n-3) !!} {2 ^ {n} n!} } right) ^ {2} h ^ {n} right] \ = pi (a + b) left [1+ sum _ {n = 1} ^ { infty} left ({ frac {(2n-1) !!} {2 ^ {n} n!}} right) ^ {2} { frac {h ^ {n}} {(2n-1) ^ {2}}} справа]. end {align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7d29d8f31216e5d32400e99b04e75e242d987893)
![{ displaystyle C приблизительно pi { biggl [} 3 (a + b) - { sqrt {(3a + b) (a + 3b)}} { biggr]} = pi { biggl [} 3 (a + b) - { sqrt {10ab + 3 left (a ^ {2} + b ^ {2} right)}} { biggr]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/86c8a7234c16af19a7338faafe61b4cf9a333f80)



![{displaystyle s=-bleft[Eleft(z;{Biggl |};1-{frac {a^{2}}{b^{2}}}right)right]_{arccos {frac {x_{1}}{a}}}^{arccos {frac {x_{2}}{a}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ed75c6daa97d1f19f90b6a53c3441bf0e65601a2)






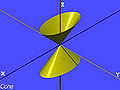




![{ displaystyle { begin {align} a = { frac {r_ {a} + r_ {p}} {2}} \ [2pt] b = { sqrt {r_ {a} r_ {p}} } \ [2pt] ell = { frac {2} {{ frac {1} {r_ {a}}} + { frac {1} {r_ {p}}}}} = { frac {2r_ {a} r_ {p}} {r_ {a} + r_ {p}}} end {align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/08835a73be73e7094f529d4eff42804930898271) .
.