Как найти радиус конуса вписанного в пирамиду - AvtoShod.ru

Конус вписан в пирамиду, если его основание вписано в основание пирамиды, а вершина совпадает с вершиной пирамиды. Соответственно, в этом случае пирамида описана около конуса.

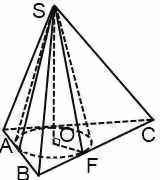
Конус может быть вписан в пирамиду, если основание пирамиды — многоугольник, в который можно вписать окружность, а вершина пирамиды проецируется в центр этой окружности. Другой вариант: конус можно вписать в пирамиду, если высоты ее боковых граней равны между собой. Отсюда, в частности, следует, что в любую правильную пирамиду можно вписать конус.

Каждая из плоскостей, содержащих боковую грань описанной пирамиды, является касательной к конусу плоскостью (то есть плоскостью, проходящей через образующую конуса перпендикулярно осевому сечению конуса, проведенному через эту образующую). Высоты боковых граней пирамиды есть образующие конуса. Высота вписанного конуса совпадает с высотой пирамиды. Радиус конуса равен радиусу вписанной в основание пирамиды окружности.

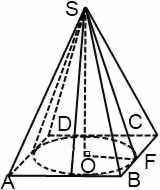
Найдем отношение объема вписанного конуса к объему пирамиды:

$[frac{{{V_k}}}{{{V_n}}} = frac{{frac{1}{3}pi {r^2}H}}{{frac{1}{3}{S_{ocn}}H}} = frac{{pi {r^2}}}{{{S_{ocn}}}}.]$

В частности, отношение объема вписанного конуса к объему правильной пирамиды для правильной треугольной пирамиды равно

$[frac{{{V_k}}}{{{V_n}}} = frac{{pi {{(frac{a}{{2sqrt 3 }})}^2}}}{{frac{{{a^2}sqrt 3 }}{4}}} = frac{{4pi {a^2}}}{{12sqrt 3 {a^2}}} = frac{pi }{{3sqrt 3 }},]$

для правильной четырехугольной пирамиды —

$[frac{{{V_k}}}{{{V_n}}} = frac{{pi {{(frac{a}{2})}^2}}}{{{a^2}}} = frac{pi }{4},]$

для правильной шестиугольной пирамиды —

$[frac{{{V_k}}}{{{V_n}}} = frac{{pi {{(frac{{asqrt 3 }}{2})}^2}}}{{frac{{3{a^2}sqrt 3 }}{2}}} = frac{pi }{{2sqrt 3 }}.]$

(Формулу площади правильного треугольника и формулу площади правильного шестиугольника легко запомнить с помощью ассоциаций).

Теперь найдем отношение площади боковой поверхности вписанного конуса к боковой поверхности правильной пирамиды. Так как апофема пирамиды m равна образующей конуса l, имеем:

$[frac{{{S_{bok.k}}}}{{{S_{bok.p}}}} = frac{{pi rl}}{{pm}} = frac{{pi r}}{p}.]$

В частности, отношение боковой поверхности вписанного конуса к боковой поверхности правильной треугольной пирамиды

$[frac{{{S_{bok.k}}}}{{{S_{bok.p}}}} = frac{{pi cdot frac{a}{{2sqrt 3 }}}}{{frac{{3a}}{2}}} = frac{pi }{{3sqrt 3 }},]$

для правильной четырехугольной пирамиды —

$[frac{{{S_{bok.k}}}}{{{S_{bok.p}}}} = frac{{pi cdot frac{a}{2}}}{{2a}} = frac{pi }{4},]$

для правильной шестиугольной пирамиды —

$[frac{{{S_{bok.k}}}}{{{S_{bok.p}}}} = frac{{pi cdot frac{{asqrt 3 }}{2}}}{{3a}} = frac{pi }{{2sqrt 3 }}.]$

Источник

felybamefri960

Вопрос по геометрии:

В правильную треугольную пирамиду вписан конус. Найти радиус основания конуса, если ребро пирамиды равно 4см и угол между соседними боковыми ребрами равен 60°

Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?

Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!

Ответы и объяснения 1

cenghalisl

Если правильно условие, тогда так. Смотри рисунок

Знаете ответ? Поделитесь им!

Гость

Гость ?

Как написать хороший ответ?

Чтобы добавить хороший ответ необходимо:

Отвечать достоверно на те вопросы, на которые знаете
правильный ответ;
Писать подробно, чтобы ответ был исчерпывающий и не
побуждал на дополнительные вопросы к нему;
Писать без грамматических, орфографических и
пунктуационных ошибок.

Этого делать не стоит:

Копировать ответы со сторонних ресурсов. Хорошо ценятся
уникальные и личные объяснения;
Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не
знаю» и так далее;
Использовать мат — это неуважительно по отношению к
пользователям;
Писать в ВЕРХНЕМ РЕГИСТРЕ.

Есть сомнения?

Не нашли подходящего ответа на вопрос или ответ отсутствует?
Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие
вопросы в разделе Геометрия.

Трудности с домашними заданиями? Не стесняйтесь попросить о помощи —
смело задавайте вопросы!

Геометрия — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения.

Источник

В любой конус можно вписать бесконечное множество цилиндров (радиусы цилиндров меньше радиуса конуса).

Чертится осевое сечение.

Центры оснований конуса и цилиндра совпадают, а высота и радиусы различаются.

Чтобы определить зависимость между радиусами или высотами конуса и цилиндра, в задаче должна присутствовать дополнительная информация.

Около конуса можно описать только такую пирамиду, у которой двугранные углы при основании равны (при условии, что основание высоты пирамиды не находится вне многоугольника в основании пирамиды).

Двугранные углы при основании равны у правильных пирамид и у таких пирамид, высота которых проецируется в центр вписанной окружности.

Радиус конуса — радиус окружности, вписанной в многоугольник основания пирамиды.

Любую правильную пирамиду можно описать около конуса.
Окружность основания конуса вписана в многоугольник основания пирамиды.

Центр вписанной в треугольник окружности является точкой пересечения его биссектрис. В любой треугольник можно вписать окружность.

Центр вписанной в четырёхугольник окружности является точкой пересечения его биссектрис. Окружность можно вписать только в такой четырёхугольник, у которого равны суммы длин противоположных сторон.

Центр окружности, вписанной в квадрат и в ромб, лежит на пересечении его диагоналей.

Пирамидой, вписанной в конус, называется такая пирамида, многоугольник основания которой вписан в окружность основания конуса, а вершиной является вершина конуса.

В конус можно вписать только такую пирамиду, боковые рёбра которой равны (совпадают с образующими конуса).

Боковые рёбра равны у любой правильной пирамиды и у таких пирамид, высота которых проецируется в центр описанной окружности.

Рисунки создаются в зависимости от содержания задачи, иногда достаточно изобразить только основания этих тел, т. к. высоты пирамиды и конуса равны.

Окружность основания конуса описана около многоугольника основания пирамиды.

Радиус конуса — радиус окружности, описанной около многоугольника основания пирамиды.

Центром окружности, описанной около треугольника, является точка пересечения серединных перпендикуляров к сторонам треугольника.

Окружность можно описать около любого треугольника.

Центром окружности, описанной около четырёхугольника, является точка пересечения серединных перпендикуляров к сторонам четырёхугольника.

Окружность можно описать только около такого четырёхугольника, у которого суммы противоположных углов равны

180°

Окружность можно описать около всех равнобедренных трапеций, прямоугольников и квадратов.

Источник

Примечание. Текст задачи взят с форума.

Задача.

В правильной треугольной пирамиде угол наклона боковой грани к плоскости основания равен 60 градусов. Найти боковую поверхность вписанного в пирамиду конуса, если расстояние от основания высоты до середины бокового ребра равно корень из 7.

Решение.

Пусть нам дана правильная пирамида с треугольником ABC в основании и вершиной K

Из вершины К опустим высоту, которая пересечет основание в точке О.

Из вершины бокового ребра опустим высоту KN.

По условию задачи, отрезок OM равен √7.

Поскольку KO — высота, то треугольник KON — прямоугольный, а OM -является медианой прямоугольного треугольника.

Согласно свойствам прямоугольного треугольника, его медиана, опущенная на гипотенузу, равна радиусу описанной окружности и, одновременно, половине гипотенузы.

Таким образом:

OM = ON = √7

Соответственно, высота ребра равна 2√7

Поскольку угол ONM = 60º, а треугольник KON — прямоугольный, то

ON / KN = cos 60

По таблице значений тригонометрический функций найдем значение косинуса 60 градусов. Он равен 1/2.

Откуда

OK = KN x cos 60 = 2√7 x 1/2 = √7

Вписанный в данную пирамиду конус будет иметь длину образующей, равной высоте ребра пирамиды, а радиус, равный радиусу вписанной окружности.

Соответственно, площадь боковой поверхности конуса равна:

S = πRl

S = π * √7 * 2√7 = 14π

Ответ: площадь боковой поверхности конуса, вписанного в заданную пирамиду, равна 14π

Правильный тетраэдр (пирамида) |

Описание курса

| Правильная пирамида

Источник

Пирамида, вписанная в конус

Пирамида называется вписанной в конус, если ее основание вписано в основание конуса, а вершина совпадает с вершиной конуса. При этом конус называется описанным около пирамиды.

Около пирамиды можно описать конус тогда и только тогда, когда около ее основания можно описать окружность.

В режиме слайдов ответы и решения появляются после кликанья мышкой

Упражнение 1

Найдите сторону основания правильной треугольной пирамиды, вписанной в конус, радиус основания которого равен 1.

Ответ:

Упражнение 2

Найдите сторону основания правильной четырехугольной пирамиды, вписанной в конус, радиус основания которого равен 1.

Ответ:

Упражнение 3

Найдите сторону основания правильной шестиугольной пирамиды, вписанной в конус, радиус основания которого равен 1.

Ответ: 1.

Пирамида, описанная около конуса

Пирамида называется описанной около конуса, если ее основание описано около основания конуса, а вершина совпадает с вершиной конуса. При этом конус называется вписанным в пирамиду.

В пирамиду можно вписать конус тогда и только тогда, когда в ее основание можно вписать окружность.

Упражнение 1

Найдите сторону основания правильной треугольной пирамиды, описанной около конуса, радиус основания которого равен 1.

Ответ:

Упражнение 2

Найдите сторону основания правильной четырехугольной пирамиды, описанной около конуса, радиус основания которого равен 1.

Ответ: 2.

Упражнение 3

Найдите сторону основания правильной шестиугольной пирамиды, описанной около конуса, радиус основания которого равен 1.

Ответ:

Сфера, вписанная в конус

Сфера называется вписанной в конус, если она касается его основания и боковой поверхности (касается каждой образующей). При этом конус называется описанным около сферы.

В любой конус (прямой, круговой) можно вписать сферу. Ее центр находится на высоте конуса, а радиус равен радиусу окружности, вписанной в треугольник, являющийся осевым сечением конуса.

Напомним, что радиус r окружности, вписанный в треугольник, находится по формуле

где S – площадь, p – полупериметр треугольника.

Упражнение 1

В конус, радиус основания которого равен 1, а образующая равна 2, вписана сфера. Найдите ее радиус.

Решение. Треугольник SAB равносторонний. Высота SH равна Площадь S равна Полупериметр p равен 3. По формуле r = S/p получаем

Упражнение 2

В конус, радиус основания которого равен 2, вписана сфера радиуса 1. Найдите высоту конуса.

Решение. Обозначим h высоту SH конуса . Из формулы r = S/p имеем:

где r = 1, a = FG = 4, p =

Решая уравнение

находим

Упражнение 3

Радиус основания конуса равен 1. Образующая наклонена к плоскости основания под углом 45 о . Найдите радиус вписанной сферы.

Решение. Высота SH конуса равна 1. Образующая .

Полупериметр p равен

По формуле r = S/p , имеем

Ответ:

Упражнение 4

Высота конуса равна 8, образующая 10. Найдите радиус вписанной сферы.

Решение. Радиус основания конуса равен 6. Площадь треугольника SFG равна 48, полупериметр 16. По формуле r = S/p имеем r = 3.

Ответ: r = 3.

Упражнение 5

Можно ли вписать сферу в наклонный конус?

Ответ: Нет.

Сфера, вписанная в усеченный конус

Сфера называется вписанной в усеченный конус, если она касается его основани й и боковой поверхности (касается каждой образующей). При этом усеченный конус называется описанным около сферы.

В усеченный конус можно вписать сферу, если в его осевое сечение можно вписать окружность. Радиус этой окружности будет равен радиусу вписанной сферы.

Упражнение 1

В усеченный конус, радиусы оснований которого равны 2 и 1, вписана сфера. Найдите радиус сферы и высоту усеченного конуса.

Решение. Имеем: A 1 B = A 1 O 1 = 2, A 2 B = A 2 O 2 = 1. Следовательно, A 1 A 2 = 3 , A 1 C = 1.

Таким образом,

Упражнение 2

В усеченный конус, радиус одного основания которого равен 2, вписана сфера радиуса 1. Найдите радиус второго основания.

Решение. Пусть A 1 O 1 = 2. Обозначим r = A 2 O 2 . Имеем: A 1 A 2 = 2+ r , A 1 C = 2 – r . По теореме Пифагора, имеет место равенство из которого следует, что выполняется равенство Решая полученное уравнение относительно r , находим

Упражнение 3

В усеченном конусе радиус большего основания равен 2, образующая наклонена к плоскости основания под углом 60 о . Найдите радиус вписанной сферы.

Решение. Заметим, что осевым сечением конуса, из которого получен усеченный конус, является равносторонний треугольник со стороной 2. Радиус r сферы, вписанной в усеченный конус, равен радиусу окружности, вписанной в этот равносторонний треугольник, т.е.

Упражнение 4

Образующая усеченного конуса равна 2, площадь осевого сечения 3. Найдите радиус вписанной сферы.

Решение. Воспользуемся формулой r = S/p , где S – площадь осевого сечения, p – полупериметр. В нашем случае S = 3 . Для нахождения полупериметра напомним, что для четырехугольника, описанного около окружности, суммы противоположных сторон равны. Значит, полупериметр равен удвоенной образующей цилиндра, т.е. p = 4. Следовательно, r = ¾.

Ответ:

Упражнение 5

Можно ли вписать сферу в усеченный наклонный конус.

Ответ: Нет.

Сфера, описанная около конуса

Сфера называется описанной около конуса, если вершина и окружность основания конуса лежат на сфере. При этом конус называется вписанным в сферу .

Около любого конуса (прямого, кругового) можно описать сферу. Ее центр находится на высоте конуса, а радиус равен радиусу окружности, описанной около треугольника, являющимся осевым сечением конуса.

Напомним, что радиус R окружности, описанной около треугольника, находится по формуле

где S – площадь, a , b , c – стороны треугольника.

Упражнение 1

Около конуса, радиус основания которого равен 1, а образующая равна 2, описана сфера. Найдите ее радиус.

Решение. Треугольник SAB равносторонний со стороной 2. Высота SH равна Площадь S равна По формуле R = abc /4 S получаем

Упражнение 2

Около конуса, радиус основания которого равен 4, описана сфера радиуса 5. Найдите высоту h конуса.

Решение. Имеем, OB = 5 , HB = 4. Следовательно, OH = 3. Учитывая, что SO = OB = 5, получаем h = 8.

Ответ: h = 8.

Упражнение 3

Радиус основания конуса равен 1. Образующая наклонена к плоскости основания под углом 45 о . Найдите радиус описанной сферы.

Решение. Треугольник SAB – прямоугольный, равнобедренный. Следовательно, радиус R описанной сферы равен радиусу основания цилиндра, т.е. R = 1.

Ответ: R = 1.

Упражнение 4

Высота конуса равна 8, образующая 10. Найдите радиус описанной сферы.

Решение. В треугольнике SAB имеем: SA = SB = 10, SH = 8. По теореме Пифагора, AH = 6 и, следовательно, S = 48. Используя формулу R = abc /4 S , получаем

Упражнение 5

Можно ли описать сферу около наклонного конуса?

Ответ: Да.

Сфера, описанная около усеченного конуса

С фера называется описанной около усеченного конуса, если окружност и основани й усеченного конуса лежат на сфере. При этом усеченный к онус называется в писанным в сферу.

Около усеченного конуса можно описать сферу, если около его осевого сечения можно описать окружность. Радиус этой окружности будет равен радиусу описанной сферы.

Упражнение 1

Около усеченного конуса, радиусы оснований которого равны 2 и 1, а образующая равна 2, описана сфера. Найдите ее радиус.

Решение. Заметим, что A 1 O 1 B 2 O 2 и O 1 B 1 B 2 A 2 – ромбы. Треугольники A 1 O 1 A 2 , O 1 A 2 B 2 , O 1 B 1 B 2 – равносторонние и, значит, A 1 B 1 –диаметр. Следовательно, R = 2.

Ответ: R = 2,

Упражнение 2

Радиус меньшего основания усеченного конуса равен 1, образующая равна 2 и составляет угол 45 о с плоскостью другого основания. Найдите радиус описанной сферы.

Решение. Имеем A 2 O 2 = 1, A 1 A 2 = 2, O 1 O 2 = , OO 1 = O 1 C = 1. Следовательно, OO 2 = 1 + и, значит,