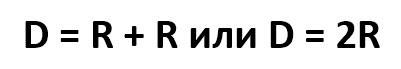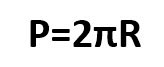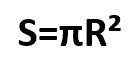Как найти радиус изделия - AvtoShod.ru - решение различных проблем

Как найти радиус окружности

Лайфхакер собрал девять способов, которые помогут справиться с геометрическими задачами.

Выбирайте формулу в зависимости от известных величин.

Через площадь круга

Разделите площадь круга на число пи.
Найдите корень из результата.

Иллюстрация: Лайфхакер

R — искомый радиус окружности.
S — площадь круга. Напомним, кругом называют плоскость внутри окружности.
π (пи) — константа, равная 3,14.

Через длину окружности

Умножьте число пи на два.
Разделите длину окружности на результат.

Иллюстрация: Лайфхакер

R — искомый радиус окружности.
P — длина окружности (периметр круга).
π (пи) — константа, равная 3,14.

Через диаметр окружности

Если вы вдруг забыли, радиус равняется половине диаметра. Поэтому, если диаметр известен, просто разделите его на два.

Иллюстрация: Лайфхакер

R — искомый радиус окружности.
D — диаметр.

Через диагональ вписанного прямоугольника

Диагональ прямоугольника является диаметром окружности, в которую он вписан. А диаметр, как мы уже вспомнили, в два раза больше радиуса. Поэтому достаточно разделить диагональ на два.

Иллюстрация: Лайфхакер

R — искомый радиус окружности.
d — диагональ вписанного прямоугольника. Напомним, она делит фигуру на два прямоугольных треугольника и является их гипотенузой — стороной, лежащей напротив прямого угла. Поэтому, если диагональ неизвестна, её можно найти через соседние стороны прямоугольника с помощью теоремы Пифагора.
a, b — стороны вписанного прямоугольника.

Через сторону описанного квадрата

Сторона описанного квадрата равна диаметру окружности. А диаметр — повторимся — равен двум радиусам. Поэтому разделите сторону квадрата на два.

Иллюстрация: Лайфхакер

r — искомый радиус окружности.
a — сторона описанного квадрата.

Через стороны и площадь вписанного треугольника

Перемножьте три стороны треугольника.
Разделите результат на четыре площади треугольника.

Иллюстрация: Лайфхакер

R — искомый радиус окружности.
a, b, с — стороны вписанного треугольника.
S — площадь треугольника.

Через площадь и полупериметр описанного треугольника

Разделите площадь описанного треугольника на его полупериметр.

Иллюстрация: Лайфхакер

r — искомый радиус окружности.
S — площадь треугольника.
p — полупериметр треугольника (равен половине от суммы всех сторон).

Через площадь сектора и его центральный угол

Умножьте площадь сектора на 360 градусов.
Разделите результат на произведение пи и центрального угла.
Найдите корень из полученного числа.

Иллюстрация: Лайфхакер

R — искомый радиус окружности.
S — площадь сектора круга.
α — центральный угол.
π (пи) — константа, равная 3,14.

Через сторону вписанного правильного многоугольника

Разделите 180 градусов на количество сторон многоугольника.
Найдите синус полученного числа.
Умножьте результат на два.
Разделите сторону многоугольника на результат всех предыдущих действий.

Иллюстрация: Лайфхакер

R — искомый радиус окружности.
a — сторона правильного многоугольника. Напомним, в правильном многоугольнике все стороны равны.
N — количество сторон многоугольника. К примеру, если в задаче фигурирует пятиугольник, как на изображении выше, N будет равняться 5.

Читайте также 📐✂️📌

Как найти периметр прямоугольника
Как научить ребёнка считать играючи
Как перевести обычную дробь в десятичную
6 способов посчитать проценты от суммы с калькулятором и без
9 логических задач, которые по зубам только настоящим интеллектуалам

Источник

Загрузить PDF

Радиус круга – это расстояние от центра круга до любой точки, которая лежит на внешней окружности круга.^[1] Простейший способ найти радиус – разделить диаметр пополам. Если диаметр не известен, но даны значения других величин, таких как длина окружности () или площадь круга ( $A=pi (r^{{2}})$ ), радиус можно вычислить по специальным формулам, изолировав переменную . Наконец, если дан центральный угол и площадь сектора круга, можно воспользоваться формулой $A={frac {theta }{360}}(pi )(r^{{2}})$ , чтобы найти радиус. Обратите внимание, что в данной статье площадь обозначена как , но в российских учебниках принято обозначение .

1
2

В формуле изолируйте радиус. Для этого разделите обе части формулы на . Вы получите формулу для вычисления радиуса.
3
В формулу подставьте значение длины окружности. Оно должно быть дано в задаче. Значение длины окружности подставляется вместо переменной .
- Например, если длина окружности равна 15 см, формула запишется так: $r={frac {15}{2pi }}$ .
4

Округлите результат. Рассчитайте величину радиуса, используя клавишу на калькуляторе и округлите ответ. Если у вас нет калькулятора или на нем нет такой клавиши, рассчитайте вручную, приняв равным 3,14.

Реклама

1

Запишите формулу для вычисления площади круга. Формула: $A=pi (r^{{2}})$ , где – площадь круга, – радиус круга.^[3]
2

В формуле изолируйте радиус.
3
В формулу подставьте значение площади. Оно должно быть дано в задаче. Значение площади подставляется вместо переменной .
- Например, если площадь круга равна 21 см², то формула запишется так: $r={sqrt {{frac {21}{pi }}}}$ .
4

Разделите площадь на . Чтобы получить точное значение, воспользуйтесь калькулятором. Если калькулятора нет, округлите до 3,14.
5
Извлеките квадратный корень. Для этого понадобится калькулятор, потому что в результате получится десятичная дробь. Так вы вычислите радиус круга.
- Например, . Таким образом, радиус круга, площадь которого равна 21 см², приблизительно равен 2,59 см.
Реклама

1
Найдите диаметр круга. Как правило, диаметр дан в задаче; в противном случае просто измерьте его. Диаметр – это отрезок, который соединяет две точки, лежащие на окружности, и проходит через центр окружности (круга).^[4] Диаметр делит круг на две равные части.
- Например, дан круг диаметром 4 см.
2
Разделите диаметр на 2. Радиус круга равен половине его диаметра.^[5]
- Например, если диаметр равен 4 см, то: $r={frac {4}{2}}=2$ . Таким образом, радиус круга равен 2 см.
Реклама

1

Запишите формулу для вычисления площади сектора. Формула: $A={frac {theta }{360}}(pi )(r^{{2}})$ , где – площадь сектора, – центральный угол, – радиус круга.^[6]
2
3

Разделите центральный угол на 360. Так вы определите, какую часть круга занимает сектор.
4
Изолируйте $(pi )(r^{{2}})$ . Для этого разделите обе части формулы на обыкновенную дробь или десятичную дробь, равную части, которую занимает сектор на круге. Если вы не пользуетесь калькулятором, делите на обыкновенную дробь. С помощью калькулятора можно разделить на десятичную дробь, но помните, что чем меньше цифр после десятичной запятой, тем менее точный результат вы получите.
- Например:
  $50=0,3333(pi )(r^{{2}})$
  ${frac {50}{0,3333}}={frac {0,3333(pi )(r^{{2}})}{0,3333}}$
  
  $150=(pi )(r^{{2}})$
5
Разделите обе части формулы на . Так вы изолируете переменную . Чтобы получить более точный результат, воспользуйтесь калькулятором. Число округлите до 3,14159 или до 3,14.
- Например:
  $150=(pi )(r^{{2}})$
  $150=(3,14159)(r^{{2}})$
  
  ${frac {150}{3,14159}}={frac {(3,14159)(r^{{2}})}{3,14159}}$
  
  $47,7465=r^{{2}}$
6
Извлеките квадратный корень из обеих частей формулы. Так вы найдете радиус круга.
- Например:
  $47,7465=r^{{2}}$
  ${sqrt {47,7465}}={sqrt {r^{{2}}}}$
  
  Таким образом, радиус круга приблизительно равен 6,91 см.
Реклама

Об этой статье

Эту страницу просматривали 681 989 раз.

Была ли эта статья полезной?

Источник

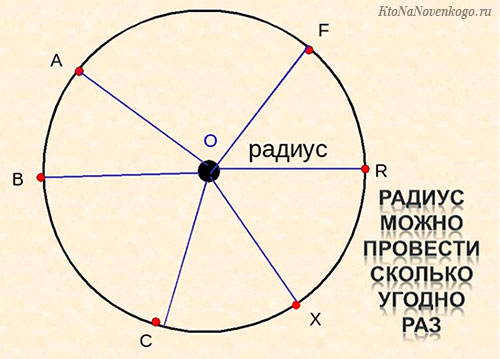
Радиус — это важнейший элемент окружности

Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru.

Сегодня мы продолжим знакомить вас с различными математическими терминами. И расскажем, что такое РАДИУС.

На самом деле эту тему проходят еще в начальных классах обычной школы. И все, кто хорошо учился, сразу смогут сказать, о чем идет речь. Ну, или хотя бы точно понять, что РАДИУС как-то связан с окружностью.

Что такое радиус

И действительно:

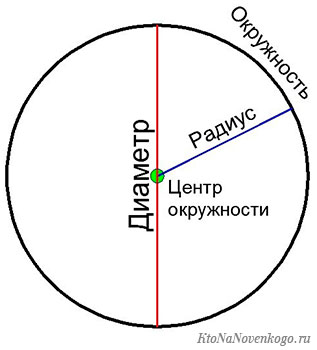
Радиус – это отрезок, который начинается в центре окружности и заканчивается в любой точке ее поверхности. В то же время так называется и длина этого отрезка.

Вот так это выглядит графически.

Само слово это имеет латинские корни. Оно произошло от «radius», что можно перевести как «луч» или «спица колеса». Впервые этот математический термин ввел французский ученый П.Ромус. Было это в 1569 году.

Но потребовалось чуть более ста лет, чтобы слово РАДИУС прижилось и стало общепринятым.

Кстати, есть еще несколько значений слова:

Размер охвата чего-нибудь или сфера распространения. Например, говорят «Огонь уничтожил все в радиусе 10 километров» или «ОН показал на карте радиус действия артиллерии»;
В анатомии этим словом обозначают Лучевую кость предплечья.

Но, конечно, нас интересует РАДИУС как математический термин. А потому и продолжим говорить именно о нем.

Радиус и диаметр

Радиус в математике всегда обозначается латинской буквой «R» или «r». Принципиальной разницы, большую букву писать или маленькую, нет.

А два соединенных вместе радиуса, которые к тому же находятся на одной прямой, называются диаметром. Или по-другому:

Диаметр – это отрезок, который проходит через центр окружности и соединяет две противоположные точки на ее поверхности. По аналогии с радиусом под диаметром подразумевают и длину этого отрезка.

Обозначается диаметр также первой буквой своего слова – D или d.

Исходя из определения диаметра, можно сделать простой вывод, который одновременно является одной из базовых основ геометрии.

А именно:

Длина диаметра равна удвоенной длине радиуса.

Свойства радиуса

В отношении него действуют несколько важных правил:

Радиус составляет половину диаметра. Это мы продемонстрировали только что.
У окружности может быть сколько угодно радиусов. Но все они будут равны по длине между собой.
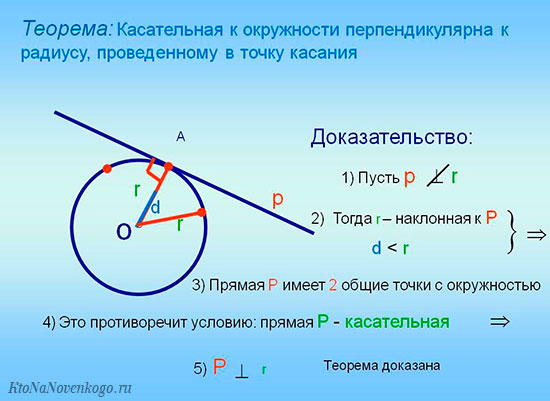
Если в точке пересечения радиуса с поверхностью окружности провести касательную, то эти две линии будут пересекаться под прямым углом. Доказательство этой теоремы наглядно приводится на следующем рисунке.
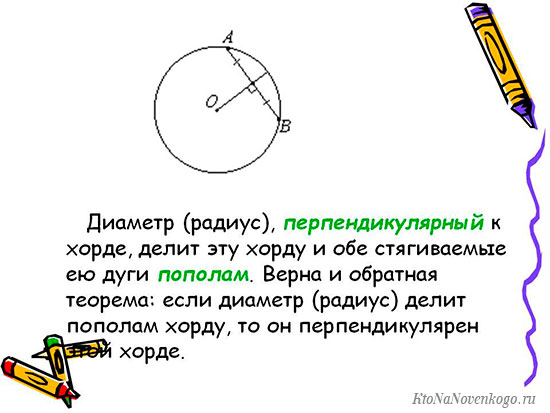
Радиус, который перпендикулярен хорде, делит ее на две равные части.

Напомним, хордой называется любой отрезок, который проходит через две точки на поверхности окружности, но не через центр. Этим она принципиально отличается от диаметра.

Длина и площадь окружности через радиус

Об этих математических величинах мы решили рассказать не случайно. Дело в том, что при их вычислении просто необходимо знать значение радиуса. И наоборот, зная длину окружности или ее площадь, можно найти радиус.

Длина окружности

Длина окружности – это кривая, которая состоит из точек, равноудаленных от центра окружности. Проще говоря, это длина поверхности окружности.

Длина окружности одновременно является и ее периметром, а потому в геометрии она обозначается латинской буквой «Р» (иногда встречаются и «L», и «C»). А формула для ее вычисления выглядит следующим образом:

Иногда ее пишут и как P=πD, так как 2R – это удвоенный радиус, что, как мы уже сказали выше, является диаметром. Но классическая формула во всех учебниках дается все-таки через радиус.

Гораздо интереснее здесь рассмотреть величину, обозначаемую буквой π. Это как многим известно, математическая постоянная. Она произносится как «Пи» и равна 3,14.

Хотя на самом деле количество знаков после запятой у «пи» не ограничено. Но для простоты вычислений решено брать именно так.

Площадь окружности

Площадь окружности – это пространство, которое находится внутри ее периметра. Она обозначается латинской буквой «S». А формула для ее вычисления выглядит так:

Опять же, здесь R- это радиус, а π – математическая постоянная, равная 3,14.

Вместо заключения

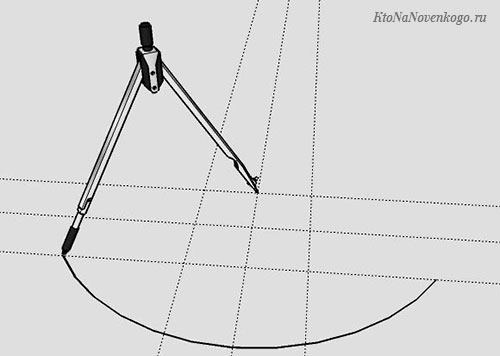
Чтобы еще больше понять, насколько важно понятие РАДИУС, вспомните инструмент, с помощью которого можно начертить окружность. Это циркуль и выглядит он вот так.

Пользоваться им просто. Ножка с острым концом ставится в центр будущей окружности. А ножка с грифелем прочерчивает линию. А расстояние, на котором они будут друг от друга, и есть РАДИУС.

Источник

Download Article

The radius of a circle is the distance from the center of the circle to any point on its circumference.^[1] The easiest way to find the radius is by dividing the diameter in half. If you don’t know the diameter but you know other measurements, such as the circle’s circumference () or area ( ${displaystyle A=pi r^{2}}$ ), you can still find the radius by using the formulas and isolating the variable.

1

Write down the circumference formula. The formula is

, where equals the circle’s circumference, and equals its radii^[2]
2

Solve for r. Use algebra to change the circumference formula until r (radius) is alone on one side of the equation:

Example

${frac {C}{2pi }}={frac {2pi r}{2pi }}$
${frac {C}{2pi }}=r$
$r={frac {C}{2pi }}$

Advertisement
3

Plug the circumference into the formula. Whenever a math problem tells you the circumference C of a circle, you can use this equation to find the radius r. Replace C in the equation with the circumference of the circle in your problem:

Example
If the circumference is 15 centimeters, your formula will look like this: $r={frac {15}{2pi }}$ centimeters
4

Round to a decimal answer. Enter your result in a calculator with the button and round the result. If you don’t have a calculator, calculate it by hand, using 3.14 as a close estimate for .

Example
$r={frac {15}{2pi }}=$ about ${frac {7.5}{2*3.14}}=$ approximately 2.39 centimeters

1

Set up the formula for the area of a circle. The formula is

$A=pi r^{{2}}$

, where equals the area of the circle, and equals the radius.^[3]
2

Solve for the radius. Use algebra to get the radius r alone on one side of the equation:

Example
Divide both sides by :
$A=pi r^{{2}}$
${frac {A}{pi }}=r^{{2}}$
Take the square root of both sides:
${sqrt {{frac {A}{pi }}}}=r$
$r={sqrt {{frac {A}{pi }}}}$
3

Plug the area into the formula. Use this formula to find the radius when the problem tells you the area of the circle. Substitute the area of the circle for the variable .

Example
If the area of the circle is 21 square centimeters, the formula will look like this: $r={sqrt {{frac {21}{pi }}}}$
4

Divide the area by . Begin solving the problem by simplifying the portion under the square root ( ${frac {A}{pi }})$ . Use a calculator with a key if possible. If you don’t have a calculator, use 3.14 as an estimate for .

Example
If using 3.14 for , you would calculate:
$r={sqrt {{frac {21}{3.14}}}}$

If your calculator allows you to enter the whole formula on one line, that will give you a more accurate answer.
5

Take the square root.

You will likely need a calculator to do this

, because the number will be a decimal. This value will give you the radius of the circle.

Example
. So, the radius of a circle with an area of 21 square centimeters is about 2.59 centimeters.
Areas always use square units (like square centimeters), but the radius always uses units of length (like centimeters). If you keep track of units in this problem, you’ll notice that ${sqrt {cm^{{2}}}}=cm$ .

1
Check the problem for a diameter. If the problem tells you the diameter of the circle, it’s easy to find the radius. If you are working with an actual circle,

measure the diameter by placing a ruler so its edge passes straight through the circle’s center

, touching the circle on both sides.^[4]
- If you’re not sure where the circle center is, put the ruler down across your best guess. Hold the zero mark of the ruler steady against the circle, and slowly move the other end back and forth around the circle’s edge. The highest measurement you can find is the diameter.
- For example, you might have a circle with a diameter of 4 centimeters.
2
Divide the diameter by two. A circle’s

radius is always half the length of its diameter.

^[5]
- For example, if the diameter is 4 cm, the radius equals 4 cm ÷ 2 = 2 cm.
- In math formulas, the radius is r and the diameter is d. You might see this step in your textbook as $r={frac {d}{2}}$ .

1

Set up the formula for the area of a sector. The formula is

$A_{{sector}}={frac {theta }{360}}(pi )(r^{{2}})$

, where $A_{{sector}}$ equals the area of the sector, equals the central angle of the sector in degrees, and equals the radius of the circle.^[6]
2

Plug the sector’s area and central angle into the formula. This information should be given to you.

Make sure you have the area of the sector, not the area for the circle.

Substitute the area for the variable $A_{{sector}}$ and the angle for the variable .

Example
If the area of the sector is 50 square centimeters, and the central angle is 120 degrees, you would set up the formula like this:
$50={frac {120}{360}}(pi )(r^{{2}})$ .
3

Divide the central angle by 360. This will tell you what fraction of the entire circle the sector represents.

Example
${frac {120}{360}}={frac {1}{3}}$ . This means that the sector is ${frac {1}{3}}$ of the circle.
Your equation should now look like this: $50={frac {1}{3}}(pi )(r^{{2}})$
4

Isolate $(pi )(r^{{2}})$ . To do this, divide both sides of the equation by the fraction or decimal you just calculated.

Example
$50={frac {1}{3}}(pi )(r^{{2}})$
${frac {50}{{frac {1}{3}}}}={frac {{frac {1}{3}}(pi )(r^{{2}})}{{frac {1}{3}}}}$
$150=(pi )(r^{{2}})$
5

Divide both sides of the equation by . This will isolate the variable. For a more precise result, use a calculator. You can also round to 3.14.

Example
$150=(pi )(r^{{2}})$
${frac {150}{pi }}={frac {(pi )(r^{{2}})}{pi }}$
$47.7=r^{{2}}$
6

Take the square root of both sides. This will give you the radius of the circle.

Example
$47.7=r^{{2}}$
${sqrt {47.7}}={sqrt {r^{{2}}}}$

So, the radius of the circle is about 6.91 centimeters.

Practice Problems and Answers

Add New Question

Question

How do I find the radius of a circle when I know the chord length?

It is possible to have quite a few circles, all with different radii, in which one could draw a chord of a given, fixed length. Hence, the chord length by itself cannot determine the radius of the circle.
Question

How do I find the radius of a circle when I know the arc length and the central angle?

Divide the central angle into 360°. Multiply the resulting number by the arc length. That gives you the circumference of the circle. Divide the circumference by pi. That’s the diameter. Half of the diameter is the radius of the circle.
Question

How do I calculate the radius of a circle when no other values are known?

Technically you can’t «calculate» the radius in such a situation. However, it is possible, by construction, to locate the center of such a circle, and then, simply by physically measuring, determine the radius. To do the construction, draw any two chords and construct their perpendicular bisectors; their point of intersection is the center of the circle. Then draw in any radius and measure it with a ruler. Not technically a «calculation.»

See more answers

Ask a Question

200 characters left

Include your email address to get a message when this question is answered.

Submit

About This Article

Article SummaryX

To calculate the radius of a circle by using the circumference, take the circumference of the circle and divide it by 2 times π. For a circle with a circumference of 15, you would divide 15 by 2 times 3.14 and round the decimal point to your answer of approximately 2.39. Be sure to include the units in your answer. To learn more, such as how to calculate the radius with the area or diameter, keep reading the article!

Did this summary help you?

Thanks to all authors for creating a page that has been read 3,353,920 times.

Did this article help you?

Источник

В данной публикации мы рассмотрим, как можно вычислить радиус круга (окружности) и разберем примеры решения задач для закрепления материала.

Формулы вычисления радиуса круга
- 1. Через длину окружности/периметр круга
- 2. Через площадь круга
Примеры задач

Формулы вычисления радиуса круга

1. Через длину окружности/периметр круга

Радиус круга/окружности рассчитывается по формуле:

C – это длина окружности/периметр круга; равняется удвоенному произведению числа π на его радиус:

C = 2πR

π – число, приближенное значение которого равно 3,14.

2. Через площадь круга

Радиус круга/окружности вычисляется таким образом:

S – это площадь круга; равна числу π, умноженному на квадрат его радиуса:

S = πR²

Примеры задач

Задание 1
Длина окружности равняется 87,92 см. Найдите ее радиус.

Решение:
Используем первую формулу (через периметр):

Задание 2
Найдите радиус круга, если его площадь составляет 254,34 см².

Решение:
Воспользуемся формулой, выраженной через площадь фигуры:

Источник

Как найти радиус окружности

Через площадь круга

Через длину окружности

Через диаметр окружности

Через диагональ вписанного прямоугольника

Через сторону описанного квадрата

Через стороны и площадь вписанного треугольника

Через площадь и полупериметр описанного треугольника

Через площадь сектора и его центральный угол

Через сторону вписанного правильного многоугольника

Об этой статье

Была ли эта статья полезной?

Что такое радиус

Радиус и диаметр

Свойства радиуса

Длина и площадь окружности через радиус

Длина окружности

Площадь окружности

Вместо заключения

Practice Problems and Answers

About This Article

Did this article help you?

Формулы вычисления радиуса круга

1. Через длину окружности/периметр круга

2. Через площадь круга

Примеры задач

Не пропустите также: