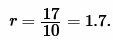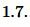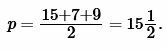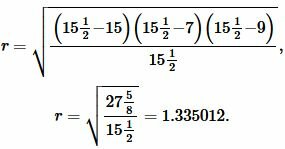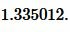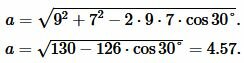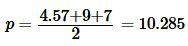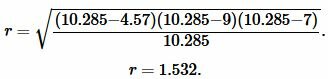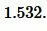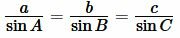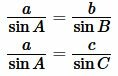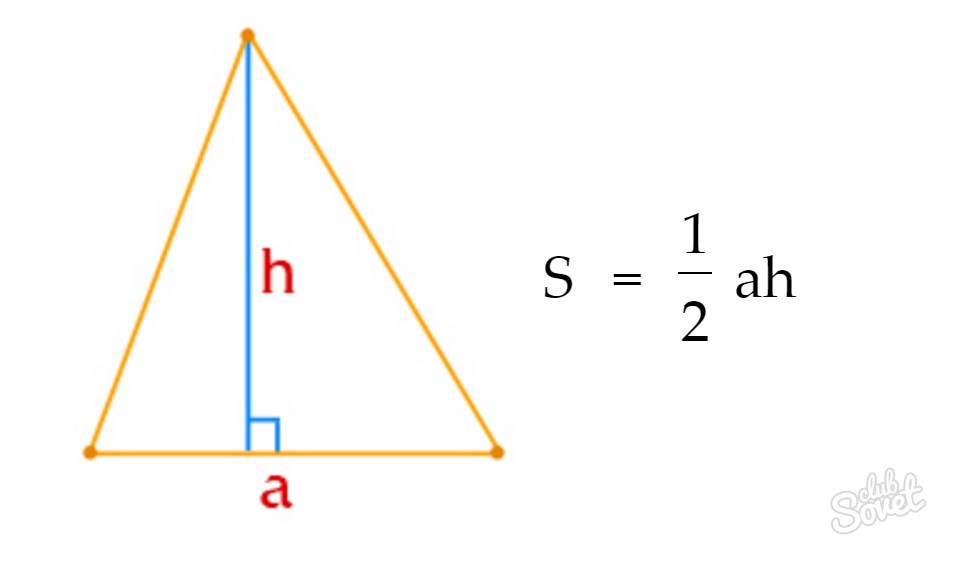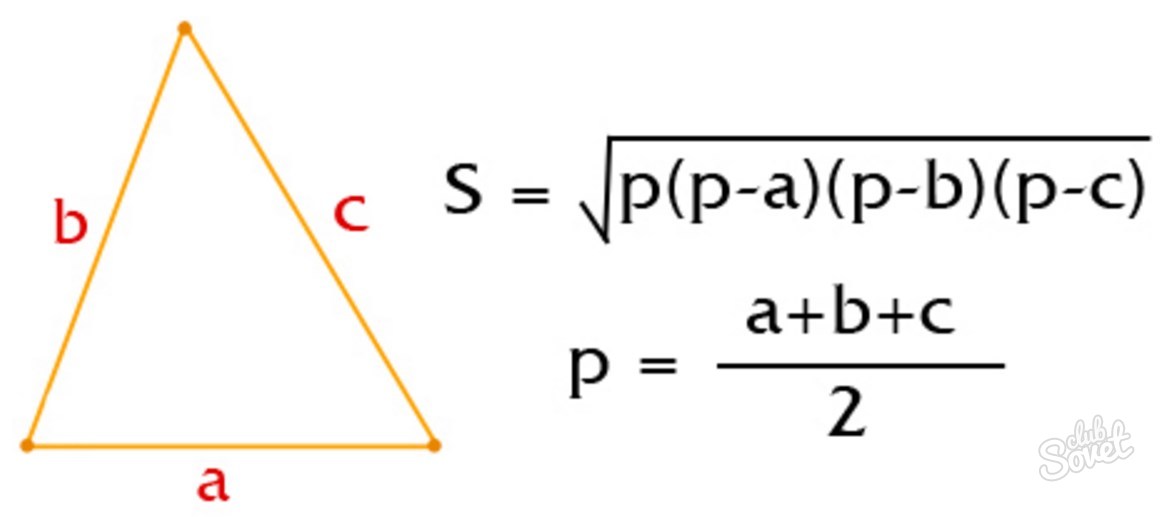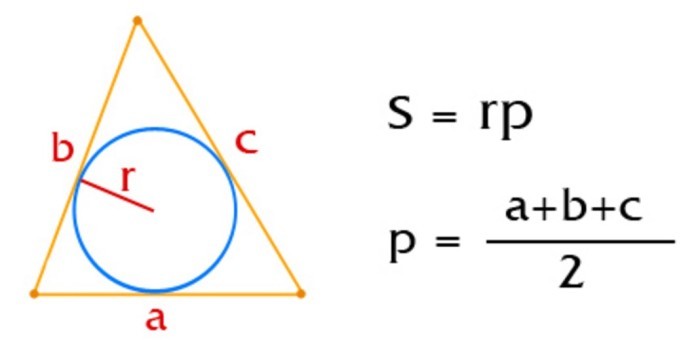Если окружность располагается внутри угла и касается его сторон, её называют вписанной в этот угол. Центр такой вписанной окружности располагается на биссектрисе этого угла.
Если же она лежит внутри выпуклого многоугольника и соприкасается со всеми его сторонами, она называется вписанной в выпуклый многоугольник.
Содержание:
- Окружность, вписанная в треугольник
- Вычисление с помощью полупериметра
- Вычисление с учётом площади треугольника
- Расчёт с помощью тригонометрических функций
- Окружность, вписанная в прямоугольный треугольник
- Видео
Окружность, вписанная в треугольник
Окружность, вписанная в треугольник, соприкасается с каждой стороной этой фигуры лишь в одной точке. В один треугольник возможно вписать лишь одну окружность.
Радиус такой окружности будет зависеть от следующих параметров треугольника:
- Длин сторон треугольника.
- Его площади.
- Его периметра.
- Величины углов треугольника.
Для того чтобы вычислить радиус вписанной окружности в треугольник, не всегда обязательно знать все перечисленные выше параметры, поскольку они взаимосвязаны между собой через тригонометрические функции.
Вычисление с помощью полупериметра
Чтобы рассчитать величину радиуса вписанной окружности в треугольник, необходимо учитывать следующие параметры:
- Если известны длины всех сторон геометрической фигуры (обозначим их буквами a, b и c), то вычислять радиус придётся путём извлечения квадратного корня.
- Приступая к вычислениям, необходимо добавить к исходным данным ещё одну переменную — полупериметр (р). Его можно рассчитать, сложив все длины и полученную сумму разделив на 2. p = (a+b+c)/2. Таким образом можно существенно упростить формулу нахождения радиуса.
- В целом формула должна включать в себя знак радикала, под который помещается дробь, знаменателем этой дроби будет величина полупериметра р.
- Числителем данной дроби будет представлять собой произведение разностей (p-a)*(p-b)*(p-c)
- Таким образом, полный вид формулы будет представлен следующим образом: r = √(p-a)*(p-b)*(p-c)/p).
Вычисление с учётом площади треугольника
Если нам известна площадь треугольника и длины всех его сторон, это позволит найти радиус интересующей нас окружности, не прибегая к извлечению корней.
- Для начала нужно удвоить величину площади.
- Результат делится на сумму длин всех сторон. Тогда формула будет выглядеть следующим образом: r = 2*S/(a+b+c).
- Если воспользоваться величиной полупериметра, можно получить совсем простую формулу: r = S/p.
Расчёт с помощью тригонометрических функций
Если в условии задачи присутствует длина одной из сторон, величина противоположного угла и периметр, можно воспользоваться тригонометрической функцией — тангенсом. В этом случае формула расчёта будет иметь следующий вид:
r = (P /2- a)* tg (α/2), где r — искомый радиус, Р — периметр, а — значение длины одной из сторон, α — величина противоположного стороне, а угла.
Радиус окружности, которую необходимо будет вписывать в правильный треугольник, можно найти по формуле r = a*√3/6.
Окружность, вписанная в прямоугольный треугольник
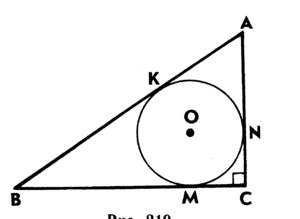
В прямоугольный треугольник можно вписать только одну окружность. Центр такой окружности одновременно служит точкой пересечения всех биссектрис. Эта геометрическая фигура имеет некоторые отличительные черты, которые необходимо учесть, вычисляя радиус вписанной окружности.
- Для начала необходимо выстроить прямоугольный треугольник с заданными параметрами. Построить такую фигуру можно по размеру её одной стороны и величинам двух углов или же по двум сторонам и углу между этими сторонами. Все эти параметры должны быть указаны в условии задачи. Треугольник обозначается как АВС, причём С — это вершина прямого угла. Катеты при этом обозначаются переменными, а и b, а гипотенуза — переменной с.
- Для построения классической формулы и вычисления радиуса окружности необходимо найти размеры всех сторон описанной в условии задачи фигуры и по ним вычислить полупериметр. Если в условиях даются размеры двух катетов, по ним можно вычислить величину гипотенузы, исходя из теоремы Пифагора.
- Если в условии дан размер одного катета и одного угла, необходимо понять, прилежащий этот угол или противолежащий. В первом случае гипотенуза находится с помощью теоремы синусов: с=a/sinСАВ, во втором случае применяют теорему косинусов с=a/cosCBA.
- Когда все расчёты выполнены и величины всех сторон известны, находят полупериметр по формуле, описанной выше.
- Зная величину полупериметра, можно найти радиус. Формула представляет собой дробь. Её числителем является произведение разностей полупериметра и каждой из сторон, а знаменателем —величина полупериметра.
Следует заметить, что числитель данной формулы является показателем площади. В этом случае формула нахождения радиуса гораздо упрощается — достаточно разделить площадь на полупериметр.
Определить площадь геометрической фигуры можно и в том случае, если известны оба катета. По сумме квадратов этих катетов находится гипотенуза, далее вычисляется полупериметр. Вычислить площадь можно, умножив друг на друга величины катетов и разделив полученное на 2.
Если в условиях даны длины и катетов и гипотенузы, определить радиус можно по очень простой формуле: для этого складываются длины катетов, из полученного числа вычитается длина гипотенузы. Результат необходимо разделить пополам.
Видео
Из этого видео вы узнаете, как находить радиус вписанной в треугольник окружности.
Все формулы для радиуса вписанной окружности
Радиус вписанной окружности в треугольник
a , b , c — стороны треугольника
p — полупериметр, p=( a + b + c )/2
Формула радиуса вписанной окружности в треугольник ( r ):
Радиус вписанной окружности в равносторонний треугольник
a — сторона треугольника
r — радиус вписанной окружности
Формула для радиуса вписанной окружности в равносторонний треугольник ( r ):
Радиус вписанной окружности равнобедренный треугольник
1. Формулы радиуса вписанной окружности если известны: стороны и угол
a — равные стороны равнобедренного треугольника
b — сторона ( основание)
α — угол при основании
О — центр вписанной окружности
r — радиус вписанной окружности
Формула радиуса вписанной окружности в равнобедренный треугольник через стороны ( r ) :
Формула радиуса вписанной окружности в равнобедренный треугольник через сторону и угол ( r ) :
2. Формулы радиуса вписанной окружности если известны: сторона и высота
a — равные стороны равнобедренного треугольника
b — сторона ( основание)
h — высота
О — центр вписанной окружности
r — радиус вписанной окружности
Формула радиуса вписанной окружности в равнобедренный треугольник через сторону и высоту ( r ) :
Радиус вписанной в треугольник окружности онлайн
С помощю этого онлайн калькулятора можно найти радиус вписанной в треугольник окружности. Для нахождения радиуса вписанной в треугольник окружности введите известные данные в ячейки и нажмите на кнопку «Вычислить». Теоретическую часть и численные примеры смотрите ниже.
Открыть онлайн калькулятор
1. Радиус вписанной в треугольник окружности, если известна площадь и полупериметр треуольника
Пусть известна площадь S треугольника и полупериметр
| ( small p=frac<large a+b+c> <large 2 >) | (1) |
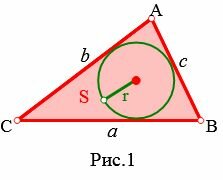
где a, b, c стороны треугольника (Рис.1).
Найдем радиус вписанной в треугольник окружности r.
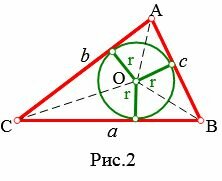
Из центра O вписанной в треугольник окружности проведем перпендикуляры к сторонам треугольника. Все эти перпендикуляры равны радиусу r вписанной в треугольник окружности (Рис.2).
Прямыми OA, OB, OC разделим треугольник ABC на три треугольника: AOC, COB, AOB. Найдем площадь треугольников AOC, COB, AOB:
| ( small S_=frac<large 1> <large 2>cdot r cdot b ,) ( small S_=frac<large 1> <large 2>cdot r cdot c, ) ( small S_=frac<large 1> <large 2>cdot r cdot a ) | (2) |
| ( small S=S_+S_+S_)( small =frac<large 1> <large 2>cdot r cdot b ) ( small +frac<large 1> <large 2>cdot r cdot c ) ( small +frac<large 1> <large 2>cdot r cdot a ) ( small =frac<large 1> <large 2>cdot r cdot ( a+b+c) ) | (3) |
| ( small S=r cdot p. ) | (4) |
Найдем радиус r вписанной в треугольник окружности из равенства (4):
| ( small r=frac<large S><large p>. ) | (5) |
Пример 1. Известны площадь ( small S=17 ) и полупериметр ( small p=10 ) треугольника. Найти радиус вписанной в треугольник окружности.
Решение. Для нахождения радиуса вписанной в треугольник окружности воспользуемся формулой (5).
Подставим значения ( small S=17 ) и ( small p=10 ) в (5):
Ответ:
2. Радиус вписанной в треугольник окружности, если известны все три стороны треугольника
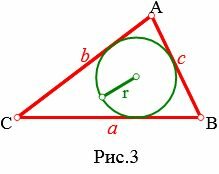
Пусть известны три стороны треугольника: a, b, c. Найдем радиус вписанной в треугольник окружности (Рис.3).
Площадь треугольника по трем сторонам вычисляется из формулы:
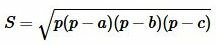 |
(6) |
где полупериметр p вычисляется из формулы (1).
Подставляя (6) в (5), получим формулу радиуса вписанной в треугольник окружности:
| ( small r=sqrt<frac<large (p-a)(p-b)(p-c)><large p>>, ) | (7) |
Пример 2. Известны стороны треугольника: ( small a=15 ,; b=7, ; c=9.) Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанный в треугольник найдем сначала полупериметр треугольника из формулы (1):
Подставим значения ( small a,; b, ; c, ; p ) в (7):
Ответ:
3. Радиус вписанной в треугольник окружности, если известны две стороны и угол между ними
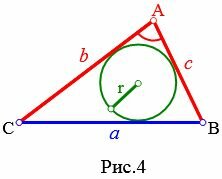
Пусть известны стороны b и c треугольника и угол A между ними (Рис.4). Найдем формулу радиуса вписанной в треугольник окружности.
Из теоремы косинусов найдем сторону a треугольника:
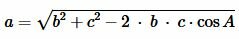 |
(8) |
Далее, для вычисления радиуса вписанной в треугольник окружности, воспользуемся формулой (7), где полупериметр p вычисляется из (1).
Пример 3. Известны стороны треугольника: ( small b=9 ,; c=7, ; ) и угол меджу ними A=30°. Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанный в треугольник найдем сначала сторону a треугольника из формулы (8):
Далее найдем p из формулы (1):
Подставим значения ( small a,; b, ; c, ; p ) в (7):
Ответ:
4. Радиус вписанной в треугольник окружности, если известны сторона и прилежащие два угла
Пусть известны сторона a треугольника и прилежащие два угла B и C (Рис.5). Найдем радиус вписанной в треугольник окружности.
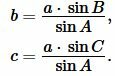 |
(9) |
Поскольку сумма углов треугольника равна 180°, то имеем ( small angle A=180°-(angle B+angle C). ) Из формул приведения тригонометрических функций имеем: ( small sin A=sin (180°-( B+ C)) ) ( small =sin (B+C). ) Тогда формулы (9) можно переписать так:
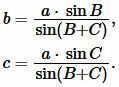 |
(10) |
Получая значения сторон b, c из (10) и значение p из (1), можно найди радиус вписанной в треугольник окружности из формулы (7). Таким образом, для нахождения радиуса вписанной в треугольник окружности через сторону и прилежащим двум углам применяется формула
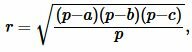 |
(11) |
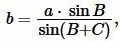 |
(12) |
 , , |
(13) |
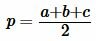 . . |
(14) |
Пример 4. Сторона треугольника равена: ( small a=7 ,) а прилежащие два угла равны соответственно ( small angle B=25°, ) ( small angle C=40°, ) Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанной в треугольник воспользуемся формулой (11). Найдем, сначала, стороны b и c из формул (12),(13). Подставим значения ( small a=7 ,) ( small angle B=25°, ) ( small angle C=40°, ) в (12) и (13):
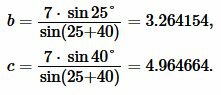
Далее найдем полупериметр p из формулы (14):
Подставляя значения a, b, c, p в (11), получим:
Ответ:
Как найти радиус окружности
О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Основные понятия
Прежде чем погружаться в последовательность расчетов, важно понять разницу между понятиями.
Окружность — замкнутая плоская кривая, все точки которой равноудалены от центра, которая лежит в той же плоскости. Если говорить проще, то это замкнутая линия, как, например, обруч и кольцо.
Круг — множество точек на плоскости, которые удалены от центра на расстоянии равном радиусу. Иначе говоря, плоская фигура, ограниченная окружностью, как мяч и блюдце.
Радиус — это отрезок, который соединяет центр окружности и любую точку на ней. Общепринятое обозначение радиуса — латинская буква R.
Возможно тебе интересно узнать — как найти длину окружности?
Формула радиуса окружности
Определить способ вычисления проще, отталкиваясь от исходных данных. Далее рассмотрим девять формул разной степени сложности.
Если известна площадь круга
R = √ S : π, где S — площадь круга, π — это константа, которая выражает отношение длины окружности к диаметру, она всегда равна 3,14.
Если известна длина
R = P : 2 * π, где P — длина (периметр круга).
Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курс подготовки к ЕГЭ по математике (профиль).
Если известен диаметр окружности
R = D : 2, где D — диаметр.
Диаметр — отрезок, который соединяет две точки окружности и проходит через центр. Радиус всегда равен половине диаметра.
Если известна диагональ вписанного прямоугольника
R = d : 2, где d — диагональ.
Диагональ вписанного прямоугольник делит фигуру на два прямоугольных треугольника и является их гипотенузой — стороной, лежащей напротив прямого угла. Если диагональ неизвестна, теорема Пифагора поможет её вычислить:
d = √ a 2 + b 2 , где a, b — стороны вписанного прямоугольника.
Если известна сторона описанного квадрата
R = a : 2, где a — сторона.
Сторона описанного квадрата равна диаметру окружности.
Если известны стороны и площадь вписанного треугольника
R = (a * b * c) : (4 * S), где a, b, с — стороны, S — площадь треугольника.
Если известна площадь и полупериметр описанного треугольника
R = S : p, где S — площадь треугольника, p — полупериметр треугольника.
Полупериметр треугольника — это сумма длин всех его сторон, деленная на два.
Если известна площадь сектора и его центральный угол
R = √ (360° * S) : (π * α), где S — площадь сектора круга, α — центральный угол.
Площадь сектора круга — это часть S всей фигуры, ограниченной окружностью с радиусом.
Если известна сторона вписанного правильного многоугольника
R = a : (2 * sin (180 : N)), где a — сторона правильного многоугольника, N — количество сторон.
В правильном многоугольнике все стороны равны.
Скачать онлайн таблицу
У каждой геометрической фигуры много формул — запомнить все сразу бывает действительно сложно. В этом деле поможет регулярное решение задач и частый просмотр формул. Можно распечатать эту таблицу и использовать, как закладку в тетрадке или учебнике, и обращаться к ней по необходимости.
http://matworld.ru/geometry/radius-vpisannoj-v-treugolnik-okruzhnosti.php
http://skysmart.ru/articles/mathematic/radius-okruzhnosti
Радиус вписанной в треугольник окружности онлайн
С помощю этого онлайн калькулятора можно найти радиус вписанной в треугольник окружности. Для нахождения радиуса вписанной в треугольник окружности введите известные данные в ячейки и нажмите на кнопку «Вычислить». Теоретическую часть и численные примеры смотрите ниже.
Содержание
- Радиус вписанной в треугольник окружности, если известна площадь и полупериметр треуольника
- Радиус вписанной в треугольник окружности, если известны все три стороны треугольника
- Радиус вписанной в треугольник окружности, если известны две стороны и угол между ними
- Радиус вписанной в треугольник окружности, если известны сторона и прилежащие два угла
1. Радиус вписанной в треугольник окружности, если известна площадь и полупериметр треуольника
Пусть известна площадь S треугольника и полупериметр
где a, b, c стороны треугольника (Рис.1).
Найдем радиус вписанной в треугольник окружности r.
Из центра O вписанной в треугольник окружности проведем перпендикуляры к сторонам треугольника. Все эти перпендикуляры равны радиусу r вписанной в треугольник окружности (Рис.2).
Прямыми OA, OB, OC разделим треугольник ABC на три треугольника: AOC, COB, AOB. Найдем площадь треугольников AOC, COB, AOB:
Тогда имеем:
или, учитывая (1):
Найдем радиус r вписанной в треугольник окружности из равенства (4):
Пример 1. Известны площадь ( small S=17 ) и полупериметр ( small p=10 ) треугольника. Найти радиус вписанной в треугольник окружности.
Решение. Для нахождения радиуса вписанной в треугольник окружности воспользуемся формулой (5).
Подставим значения ( small S=17 ) и ( small p=10 ) в (5):
Ответ:
2. Радиус вписанной в треугольник окружности, если известны все три стороны треугольника
Пусть известны три стороны треугольника: a, b, c. Найдем радиус вписанной в треугольник окружности (Рис.3).
Площадь треугольника по трем сторонам вычисляется из формулы:
где полупериметр p вычисляется из формулы (1).
Подставляя (6) в (5), получим формулу радиуса вписанной в треугольник окружности:
Пример 2. Известны стороны треугольника: ( small a=15 ,; b=7, ; c=9.) Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанный в треугольник найдем сначала полупериметр треугольника из формулы (1):
Подставим значения ( small a,; b, ; c, ; p ) в (7):
Ответ:
3. Радиус вписанной в треугольник окружности, если известны две стороны и угол между ними
Пусть известны стороны b и c треугольника и угол A между ними (Рис.4). Найдем формулу радиуса вписанной в треугольник окружности.
Из теоремы косинусов найдем сторону a треугольника:
Далее, для вычисления радиуса вписанной в треугольник окружности, воспользуемся формулой (7), где полупериметр p вычисляется из (1).
Пример 3. Известны стороны треугольника: ( small b=9 ,; c=7, ; ) и угол меджу ними A=30°. Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанный в треугольник найдем сначала сторону a треугольника из формулы (8):
Далее найдем p из формулы (1):
Подставим значения ( small a,; b, ; c, ; p ) в (7):
Ответ:
4. Радиус вписанной в треугольник окружности, если известны сторона и прилежащие два угла
Пусть известны сторона a треугольника и прилежащие два угла B и C (Рис.5). Найдем радиус вписанной в треугольник окружности.
Из теоремы синусов имеем:
Тогда:
или
Поскольку сумма углов треугольника равна 180°, то имеем ( small angle A=180°-(angle B+angle C). ) Из формул приведения тригонометрических функций имеем: ( small sin A=sin (180°-( B+ C)) ) ( small =sin (B+C). ) Тогда формулы (9) можно переписать так:
Получая значения сторон b, c из (10) и значение p из (1), можно найди радиус вписанной в треугольник окружности из формулы (7). Таким образом, для нахождения радиуса вписанной в треугольник окружности через сторону и прилежащим двум углам применяется формула
где
Пример 4. Сторона треугольника равена: ( small a=7 ,) а прилежащие два угла равны соответственно ( small angle B=25°, ) ( small angle C=40°, ) Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанной в треугольник воспользуемся формулой (11). Найдем, сначала, стороны b и c из формул (12),(13). Подставим значения ( small a=7 ,) ( small angle B=25°, ) ( small angle C=40°, ) в (12) и (13):
Далее найдем полупериметр p из формулы (14):
Подставляя значения a, b, c, p в (11), получим:
Ответ:
Смотрите также:
- Радиус описанной окружности около треугольника онлайн
- Радиус описанной окружности около равнобедренного треугольника онлайн
- Радиус описанной окружности около равностороннего треугольника онлайн
- Радиус описанной окружности около прямоугольного треугольника онлайн
Как найти радиус окружности
Лайфхакер собрал девять способов, которые помогут справиться с геометрическими задачами.
Выбирайте формулу в зависимости от известных величин.
Через площадь круга
- Разделите площадь круга на число пи.
- Найдите корень из результата.
- R — искомый радиус окружности.
- S — площадь круга. Напомним, кругом называют плоскость внутри окружности.
- π (пи) — константа, равная 3,14.
Через длину окружности
- Умножьте число пи на два.
- Разделите длину окружности на результат.
- R — искомый радиус окружности.
- P — длина окружности (периметр круга).
- π (пи) — константа, равная 3,14.
Через диаметр окружности
Если вы вдруг забыли, радиус равняется половине диаметра. Поэтому, если диаметр известен, просто разделите его на два.
- R — искомый радиус окружности.
- D — диаметр.
Через диагональ вписанного прямоугольника
Диагональ прямоугольника является диаметром окружности, в которую он вписан. А диаметр, как мы уже вспомнили, в два раза больше радиуса. Поэтому достаточно разделить диагональ на два.
- R — искомый радиус окружности.
- d — диагональ вписанного прямоугольника. Напомним, она делит фигуру на два прямоугольных треугольника и является их гипотенузой — стороной, лежащей напротив прямого угла. Поэтому, если диагональ неизвестна, её можно найти через соседние стороны прямоугольника с помощью теоремы Пифагора.
- a, b — стороны вписанного прямоугольника.
Через сторону описанного квадрата
Сторона описанного квадрата равна диаметру окружности. А диаметр — повторимся — равен двум радиусам. Поэтому разделите сторону квадрата на два.
- r — искомый радиус окружности.
- a — сторона описанного квадрата.
Через стороны и площадь вписанного треугольника
- Перемножьте три стороны треугольника.
- Разделите результат на четыре площади треугольника.
- R — искомый радиус окружности.
- a, b, с — стороны вписанного треугольника.
- S — площадь треугольника.
Через площадь и полупериметр описанного треугольника
Разделите площадь описанного треугольника на его полупериметр.
- r — искомый радиус окружности.
- S — площадь треугольника.
- p — полупериметр треугольника (равен половине от суммы всех сторон).
Через площадь сектора и его центральный угол
- Умножьте площадь сектора на 360 градусов.
- Разделите результат на произведение пи и центрального угла.
- Найдите корень из полученного числа.
- R — искомый радиус окружности.
- S — площадь сектора круга.
- α — центральный угол.
- π (пи) — константа, равная 3,14.
Через сторону вписанного правильного многоугольника
- Разделите 180 градусов на количество сторон многоугольника.
- Найдите синус полученного числа.
- Умножьте результат на два.
- Разделите сторону многоугольника на результат всех предыдущих действий.
- R — искомый радиус окружности.
- a — сторона правильного многоугольника. Напомним, в правильном многоугольнике все стороны равны.
- N — количество сторон многоугольника. К примеру, если в задаче фигурирует пятиугольник, как на изображении выше, N будет равняться 5.
Читайте также 📐✂️📌
- Как найти периметр прямоугольника
- Как научить ребёнка считать играючи
- Как перевести обычную дробь в десятичную
- 6 способов посчитать проценты от суммы с калькулятором и без
- 9 логических задач, которые по зубам только настоящим интеллектуалам
Как найти радиус вписанной окружности
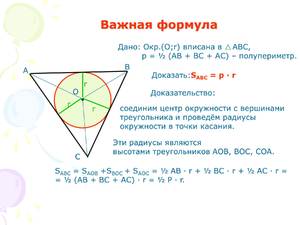
Центр пересечения биссектрис треугольника является также и центром вписанной окружности.
Биссектрисы делят треугольник на три треугольника поменьше, суммарная площадь которых, соответственно, равна площади изначального треугольника.
Высоты этих треугольников одинаковы и равны радиусу вписанной окружности. Соответственно, для того чтобы узнать радиус вписанной окружности, нам нужно узнать высоту этих треугольников.
1
Высоту этих треугольников можно получить из формулы площади, которая выглядит как S=1/2*a*h, где a – основание треугольника, а h – высота, которая в нашем случае равна r – искомой величине.
Переделав формулу под свои задачи получаем r=h=2S/a, то есть площадь треугольника делённая на половину основания. Основание каждого из этих треугольников, соответственно, является одной из сторон основного треугольника.
2
Имея заданными площадь треугольника и его стороны, а лучше сразу периметр, мы можем вычислить радиус вписанной окружности по уравнению Sabc=1/2r*(a+b+c), то есть радиус вписанной окружности равен площади основного треугольника, делённой на полупериметр, который обозначается как p.
3
Для получения радиуса вписанной окружности самым простым способом нам необходимо знать две величины – площадь данного треугольника и периметр. Если эти величины уже есть в задании, следует:
- Получить периметр путём сложения сторон.
- Разделить периметр на 2, чтобы получить полупериметр.
- Разделить площадь треугольника на полученное число.
В самом простом варианте формула выглядит как r=S/p.