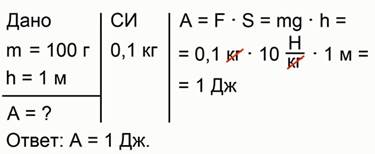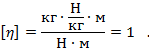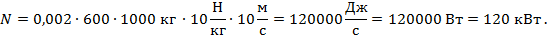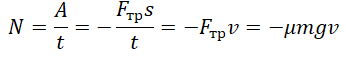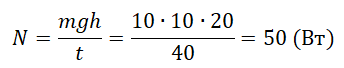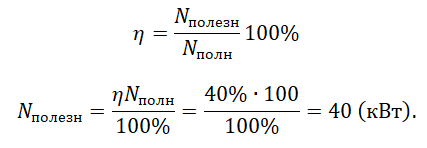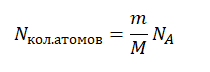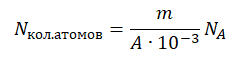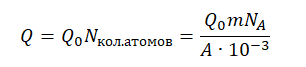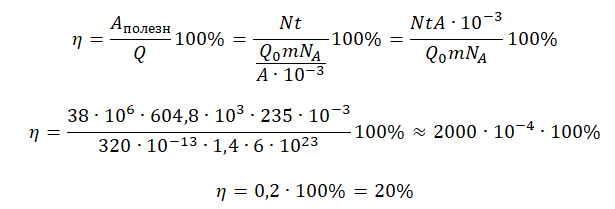Задача №1
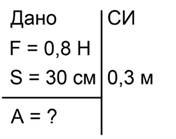
К бруску прикрепили динамометр и переместили брусок на расстояние 30 см. Показания динамометра равны 0,8 Н. Найти работу силы тяги по перемещению бруска (рис. 1).
Рис 1. К задаче №1
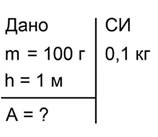
Прежде всего запишем краткое условие задачи и позаботимся, чтобы все данные были выражены в системе СИ (рис. 2).
Рис 2. Краткое условие задачи №1
Для вычисления работы воспользуемся формулой
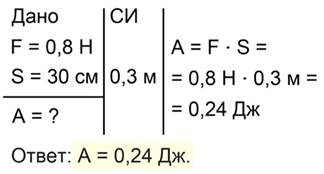
Полное решение задачи выглядит так (рис. 3).
Рис 3. Полное решение задачи №1
Задача №2
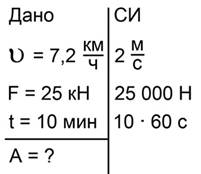
Трактор перемещает платформу со скоростью 7,2 км/ч, развивая тяговое усилие в 25 кН. Какую работу совершит трактор за 10 мин (рис. 4)?
Рис 4. К задаче №2
Запишем краткое условие задачи и переведем все единицы измерения в систему СИ (рис. 5).
Рис 5. Краткое условие задачи №2
Для вычисления работы необходимо знать расстояние, пройденное телом. В условии задачи дана скорость движения трактора и время движения, поэтому воспользуемся формулой
которую подставим в выражение для работы и получим рабочую формулу
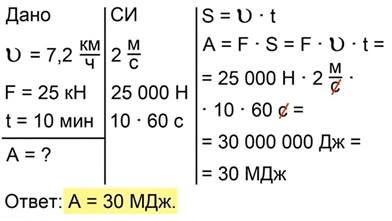
Подстановка данных из условия задачи дает
Рис 6. Полное решение задачи №2
Задача №3
Найдем работу силы тяжести при падении грузика.
Для решения задачи нам потребуется линейка и сам грузик. Измерим высоту, с которой будет падать грузик. Получаем 1 м. Масса грузика написана на нем самом и равна 100 г. Поднимем грузик на указанную высоту и отпустим его.
Краткое условие задачи будет выглядеть так (рис. 7):
Рис 7. Краткое условие задачи №3
Для нахождения работы выразим силу тяжести через массу тела , и учтем, что расстояние, пройденное телом, равно высоте, с которой оно упало:
.
Тогда
Подстановка чисел дает
Рис 8. Полное решение задачи №3
Теперь у нас есть представление о том, насколько велика работа в 1 джоуль. Такая работа совершается при падении грузика массой 100 г со стола высотой 1 м.
Переходим к решению более сложных задач.
Задача №4
Со дна реки глубиной 4 м поднимают камень объемом 0,6 м3 на поверхность. Плотность камня 2500 кг/м3, плотность воды 1000 кг/м3. Найти работу по подъему камня.
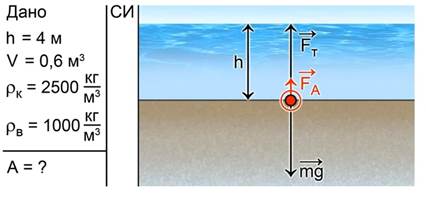
Для решения задачи необходимо не только записать краткое условие задачи, но и сделать схематический рисунок и показать силы, действующие на камень. Это сила тяги Fт (работу именно этой силы мы будем находить), сила тяжести mg и сила Архимеда Fa. Кроме того, покажем высоту, на которую сила тяги перемещает камень (рис. 9).
Рис 9. К решению задачи №4
Как видно из рисунка, искомая работа равна .
Для нахождения силы тяги воспользуемся условием равновесия тела: если оно неподвижно или движется с постоянной скоростью, то равнодействующая всех сил, приложенных к нему, равна нулю.
, откуда
.
Массу камня выразим через плотность камня и его объем, а силу Архимеда – через плотность воды и объем погруженной части камня (в этом задаче он равен объему всего камня). Объем камня и ускорение выносим за скобки.
Остается подставить силу тяги в формулу для вычисления работы
Поскольку рабочая формула получилась более сложной, единицы измерения результата определим отдельно от расчета его численного значения.
Рис 10. Полное решение задачи №4
Задача №5
Поршень двигателя перемещается на 20 см под давлением 800 кПа. Определите работу, совершаемую двигателем за один ход поршня, если площадь поршня 150 см2 (рис. 11).
Рис 11. К задаче №5
Запишем краткое условие и выразим все единицы в системе СИ (рис. 12).
Рис. 12. Краткое условие задачи №5
В данной задаче работу выполняет сила давления газа в цилиндре двигателя. Для нахождения этой силы необходимо давление в цилиндре умножить на площадь поршня. Расстояние, пройденное поршнем, мы обозначили буквой l.
Единицы измерения результата:
Численное значение результата:
Рис 13. Полное решение задачи №5
Задача №6
Найти КПД (коэффициент полезного действия) наклонной плоскости (экспериментальная) (рис. 14).
Рис. 14. Груз поднимают вверх по наклонной плоскости
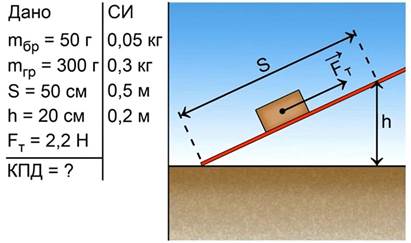
Поднимая груз по наклонной плоскости с помощью динамометра, измерим силу, которая для этого требуется. Она оказывается равной 2,2 Н. Расстояние, пройденное грузом вдоль плоскости, измеряем рулеткой. Оно составило 0,5 м. При этом груз поднялся над столом на высоту 20 см. Кроме того, известны масса бруска, равная 50 г, и общая масса трех поднимаемых грузов – 300 г.
Полученные опытные данные занесем в краткое условие задачи, выразим все величины в единицах системы СИ и сделаем схематический рисунок измерительной установки (рис. 15).
Рис 15. Краткое условие задачи №6
Коэффициентом полезного действия механизма называется физическая величина, равная отношению полезной работы, совершенной механизмом, к работе, затраченной для приведения его в действие.
КПД также обозначают греческой буквой η (эта) и часто выражают в процентах.
В нашем случае механизмом является наклонная плоскость.
Полезная работа – эта работа, которую нужно совершить, чтобы поднять тело на высоту h.
Затраченная работа совершается силой тяги, то есть силой упругости пружины динамометра.
Тогда КПД равен
Определяем единицы измерения КПД
Такой результат означает, что КПД является безразмерной величиной (просто число без единиц измерения).
Его числовое значение
Обратите внимание, что коэффициент полезного действия не может быть больше единицы, поскольку полезная работа всегда меньше затраченной. Если у вас получилось наоборот, значит, либо при измерениях, либо в ходе вычислений допущена ошибка.
Рис 16. Полное решение задачи №6
Задача №7
Трактор равномерно тянет плуг, прилагая силу в 10 кН. За 10 мин он проходит путь 1,2 км. Определить мощность, развиваемую трактором (рис. 17).
Рис 17. К условию задачи №7
Запись краткого условия и перевод величин в систему СИ будет выглядеть так (рис. 18):
Рис 18. Краткое условие задачи №7
Для нахождения мощности нужно работу, выполненную трактором, разделить на время ее выполнения. Работа вычисляется как произведение силы тяги трактора на пройденное трактором расстояние. Таким образом, получаем:
Рис 19. Полное решение задачи №7
Задача №8
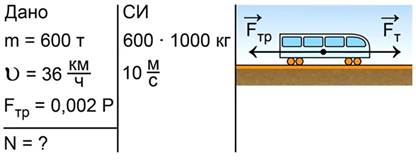
Поезд массой 600 тонн равномерно движется со скоростью 36 км/ч. Определить развиваемую тепловозом мощность, если сила трения составляет 0,002 веса поезда.
Рис. 20. К условию задачи №8
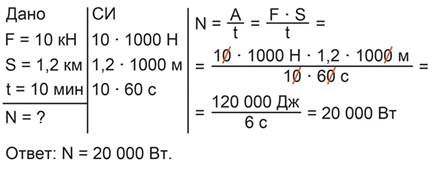
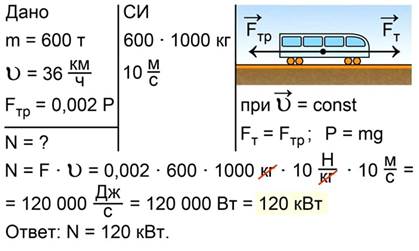
Запишем краткое условие задачи, выразим величины в единицах системы СИ, сделаем рисунок, на котором покажем силу тяги тепловоза и силу трения (рис. 21).
Рис. 21. Краткое условие задачи №8
Поскольку по условию задачи скорость поезда не изменяется и равна 36 км/ч, сила тяги равна силе трения Вес в случае движения с постоянной скоростью равен силе тяжести
Тогда сила тяги равна
Для вычисления мощности воспользуемся формулой откуда
Подстановка данных из условия дает
Рис. 22. Полное решение задачи №8
Механическая работа – это одна из основных скалярных величин в физике. В рамках стандартной школьной программы она изучается в седьмом классе в разделе механики. Механическая работа – один из способов изменения внутренней энергии тела или субстанции (например, газа или жидкости) наряду с такими формами теплопередачи, как теплопроводность, конвекция и излучение, которые изучаются в разделе тепловых явлений.
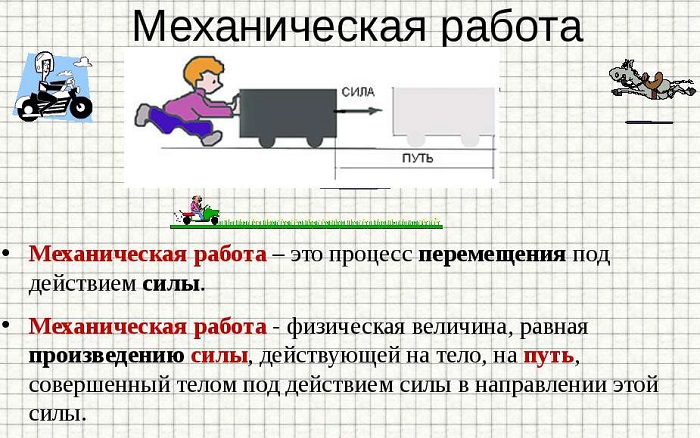
Что такое работа в физике – определение и формула
Механическая работа – это количество энергии, которое нужно затратить для того, чтобы тело начало равномерно замедляющееся движение и прошло некоторую дистанцию.
В физике механической работой называется произведение силы, которая действует на некоторое тело, на расстояние, которое оно проходит под ее воздействием:
A = F * S
В более сложных случаях в формуле появляется и третья величина – косинус угла, под которым друг к другу расположены векторы движения и приложенной силы. Найти ее значение можно по формуле:
A = F * S * cosA
В чем измеряется работа
Физические единицы, в которых выражается механическая работа, – Джоули.
Существуют разные способы для ее практического измерения, которые зависят от типа произведенного движения. При этом в формулу работы подставляют значение силы в Ньютонах и расстояния в метрах. Угол между векторами измеряют в математических единицах – градусах.
Работа силы трения
При условиях, существующих на Земле, на любое движущееся тело оказывает воздействие сила трения, замедляющая его движение. Чаще всего это трение поверхности, по которой движется объект. Это очевидно из того факта, что при воздействии постоянной силы на тело его скорость окажется переменной.
Следовательно, должна быть и другая сила, противодействующая ей – и это сила трения. Если система координат выбрана по направлению движения тела, то ее числовое значение будет отрицательным.
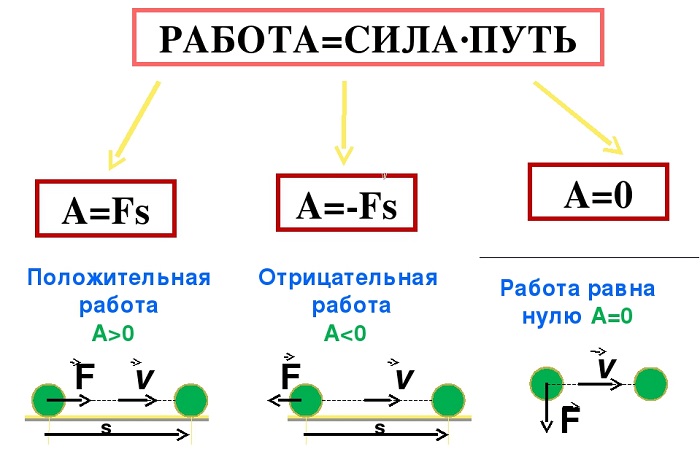
Положительная и отрицательная работа
Числовое значение работы, которую совершает сила, может становиться отрицательным в случае если ее вектор противоположен вектору скорости.
Иными словами, сила может не только придавать телу скорость для совершения движения, но и препятствовать уже совершаемому перемещению. В таком случае она будет называться противодействующей.
Полезная или затраченная работа
У тела, совершающего одно и то же действие, есть два значения работы. Первая из них, полезная, вычисляется по обычной формуле.
Вторая, затраченная, по своему понятию не имеет общей формулы для вычисления и измеряется практически. Эта разница между совершенной в реальности работой и той, которая должна была быть совершена в теории, равна коэффициенту полезного действия – КПД. Он вычисляется так:
КПД = А полезная / А затраченная,
и выражается в процентах. КПД всегда меньше 100.
Мощность
Среднее количество работы, совершаемой за единицу времени (секунду), характеризует такую величину, как мощность. Формула для ее вычисления выглядит так:
Р = A / t
В качестве работы можно подставить люблю известную формулу для ее вычисления в зависимости от ситуации. Ответ будет выражен в Ваттах.
Однако при равномерном движении можно использовать и другую формулу:
Р = F * v
Подставив вместо обычной скорости мгновенную, можно получить значение мгновенной мощности.
Примеры решения задач
Рассмотрим несколько простых задач на нахождение механической работы.
Задача 1
Какую работу совершает подъемный механизм, поднимающий десятикилограммовый блок на высоту 50 метров.
Решение:
Для того, чтобы поднять тело, необходимо преодолеть действующую на него силу тяжести. То есть F, с которой поднимают блок, равна той, с которой он притягивается к земле. Так как последняя равна m * g, то для нахождения конечного результата понадобится только одна измененная версия стандартной формулы, упомянутой выше: A = S * m * g.
При помощи простой математики найдем числовой ответ:
A = 50 м * 10 кг * 10 Н/кг;
A = 5000 Дж.
Ответ: 5000 Дж.
Впрочем, не всегда речь идет о силе тяжести.
Задача 2
Какая работа совершается силой упругости, когда пружина с жесткостью 10 Н/м, сжатая на 20 см, возвращается в исходное состояние? Система замкнута, нет никаких внешних сил, воздействующих на пружину.
Решение:
Для начала нужно найти саму F упругости, которая совершает работу. Ее формула – F = x * |k|, где x – это длина, на которую сжимается или растягивается пружина, а k – коэффициент ее жесткости. Перемещение пружины равно ее деформации, и следовательно, конечная формула в этом случае будет выглядеть так: A = S * x * k = x * x * k = x^2 * k.
Далее при помощи элементарных вычислений рассчитаем ответ:
A = (0,2 м)^2 * 10 Н/м = 0,04 * 10 = 0,4 Дж.
Ответ: 0,4 Дж.
Но во всех задачах по данной теме траектория движения тела прямая.
Задача 3
Рассчитайте, какова сила, действующая на колесо, если на то, чтобы совершить полный оборот, ему требуется 10 кДж. Диаметр диска равен 40 см, а толщина шины – 10 см.
Решение:
В этом случае нам нужно найти не А, а F, но сделать это можно при помощи все той же формулы. Возьмем точку на поверхности колеса. Предположим, что при вращательном движении ее вектор будет противоположен вектору приложения силы, а значит косинусом в формуле вновь можно пренебречь. Таким образом, за один оборот колеса точка пройдет расстояние, равное длине окружности, которую можно вычислить как 2πr или πd. Диаметр окружности можно найти из предоставленных данных: он равен сумме диаметра диска и удвоенной толщины шины, то есть 40 см + 2 * 10 см = 40 см + 20 см = 60 см = 0,6 м.
Теперь, когда мы можем вычислить расстояние, у нас есть все данные для того, чтобы приступить к нахождению силы.
Формула работы для этого случая будет такой: A = F * π * d, то силу, соответственно, можно будет выразить как F = A / (π * d).
В таком случае:
F = 10 кДж / (3,14 * 0,6 м) = 10000 Дж / 1,884 м = ~ 5308 Н.
Ответ: 5308 Н.
В завершение решим самый сложный вариант задачи, включающий в себя все, о чем говорилось выше.
Задача 4
Автомобиль Фольксваген весом 2500 кг заезжает на гору. Какова должна быть его минимальная скорость, чтобы удержаться на горе, если сила тяги равна 10 кН, время работы двигателя – 10 с, КПД – 30%, а угол наклона горы – 60 градусов. Трением и прочими силами пренебречь.
Решение:
На первый взгляд задача может показаться сложной, но для ее решения используются только простые известные формулы.
Запишем условие в более наглядном виде.
Дано:
m = 2500 кг;
F = 10000 H;
t = 10 с;
КПД = 30%;
угол A = 1500 (60+90, т. к. сила тяжести приложена под углом 90 к горизонтали);
V – ?
Выведение формулы:
Шаг 1. По условию A1 (силы тяжести) = А2 (тяги).
A1 = mg;
A2 = P * t / КПД.
То есть mg = P * t / КПД.
Шаг 2. P = F * V * cosA.
Шаг 3. Общая формула: mg = F * V * cosA * t / КПД.
V = (m * g * КПД) / (F * t * cosA).
Числовое решение:
V = (2500 кг * 10 Н/кг * 30%) / (10000 H * 10 с * cos150);
V = (2500 кг * 10 Н/кг * 0,3) / (10000 H * 10 с * cos60);
V = 7500 / 50000;
V = 0,15 м/с.
Ответ: 0,15 м/с.
Второй закон Ньютона в импульсной форме позволяет определить, как меняется скорость тела по модулю и направлению, если в течение некоторого времени на него действует определенная сила:
Работа силы
В механике также важно уметь вычислять изменение скорости по модулю, если при перемещении тела на некоторый отрезок на него действует некоторая сила. Воздействия на тела сил, приводящих к изменению модуля их скорости, характеризуется величиной, зависящей как от сил, так и от перемещений. Эту величину в механике называют работой силы.
Работа силы обозначается буквой А. Это скалярная физическая величина. Единица измерения — Джоуль (Дж).
Работа силы равна произведению модуля силы, модуля перемещения и косинусу угла между ними:
Важно!
Механическая работа совершается, если:
- На тело действует сила.
- Под действием этой силы тело перемещается.
- Угол между вектором силы и вектором перемещения не равен 90 градусам (потому что косинус прямого угла равен нулю).
Внимание! Если к телу приложена сила, но под ее действием тело не начинает движение, механическая работа равна нулю.
Пример №1. Груз массой 1 кг под действием силы 30 Н, направленной вертикально вверх, поднимается на высоту 2 м. Определить работу, совершенной этой силой.
Так как перемещение и вектор силы имеют одно направление, косинус угла между ними равен единице. Отсюда:
Работа различных сил
Любая сила, под действием которой перемещается тело, совершает работу. Рассмотрим работу основных сил в таблице.
| Работа силы тяжести |
Модуль силы тяжести: Fтяж = mg Работа силы тяжести: A = mgs cosα |
| Работа силы трения скольжения |
Модуль силы трения скольжения: Fтр = μN = μmg Работа силы трения скольжения: A = μmgs cosα |
| Работа силы упругости |
Модуль силы упругости: Fупр = kx Работа силы упругости: |
Работа силы упругости
Работа силы упругости не может быть определена стандартной формулой, так как она может применяться только для постоянной по модулю силы. Сила же упругости меняется по мере сжатия или растяжения пружины. Поэтому берется среднее значение, равное половине суммы сил упругости в начале и в конце сжатия (растяжения):
Нужно также учесть, что перемещение тела под действием силы упругости равно разности удлинения пружины в начале и конце:
s = x1 – x2
Перемещение и направление силы упругости всегда сонаправлены, поэтому угол между ними нулевой. А косинус нулевого угла равен 1. Отсюда работа силы упругости равна:
Работы силы трения покоя
Работы силы трения покоя всегда равна 0, так как под действием этой силы тело не сдвигается с места. Исключение составляет случай, когда покоящееся тело лежит на подвижном предмете, на который действует некоторая сила. Относительно системы координат, связанной с подвижным предметом, работа силы трения покоя будет нулевой. Но относительно системы отсчета, связанной с Землей, эта сила будет совершать работу, так как тело будет двигаться, оставаясь на поверхности движущегося предмета.
Пример №2. Груз массой 100 кг волоком перетащили на 10 м по плоскости, поверхность которой имеет коэффициент трения 0,4. Найти работу, совершенной силой трения скольжения.
A = μmgs cosα = 0,4∙100∙10∙10∙(–1) = –4000 (Дж) = –4 (кДж)
Знак работы силы
Знак работы силы определяется только косинусом угла между вектором силы и вектором перемещения:
- Если α = 0о, то cosα = 1.
- Если 0о < α < 90o, то cosα > 0.
- Если α = 90о, то cosα = 0.
- Если 90о < α < 180o, то cosα < 0.
- Если α = 180о, то cosα = –1.
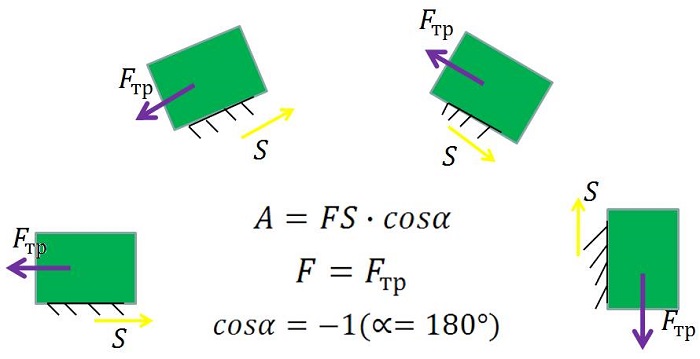
Работа силы трения скольжения всегда отрицательна, так как сила трения скольжения направлена противоположно перемещению тела (угол равен 180о). Но в геоцентрической системе отсчета работа силы трения покоя будет отличной от нуля и выше нуля, если оно будет покоиться на движущемся предмете (см. рис. выше). В таком случае сила трения покоя будет направлена с перемещением относительно Земли в одну сторону (угол равен 0о). Это объясняется тем, что тело по инерции будет пытаться сохранить покой относительно Земли. Это значит, что направление возможного движения противоположно движению предмета, на котором лежит это тело. А сила трения покоя направлена противоположно направлению возможного движения.
Геометрический смысл работы
Графическое определение
Механическая работа численно равна площади фигуры, ограниченной графиком с осями OF и OX.
A = Sфиг
Мощность
Определение
Мощность — физическая величина, показывающая, какую работу совершает тело в единицу времени. Мощность обозначается буквой N. Единица измерения: Ватт (Вт). Численно мощность равна отношению работы A, совершенной телом за время t:
Рассмотрим частные случаи определения мощности в таблице.
Мощность при равномерном прямолинейном движении тела |
Работа при равномерном прямолинейном движении определяется формулой: A = Fтs Fт — сила тяги, s — перемещение тела под действием этой силы. Отсюда мощность равна: |
Мощность при равномерном подъеме груза |
Когда груз поднимается, совершается работа, по модулю равная работе силе тяжести. За перемещение в этом случае можно взять высоту. Поэтому: |
Мгновенная мощность при неравномерном движении |
Выше мы уже получили, что мощность при постоянной скорости равна произведению этой скорости на силу тяги. Но если скорость постоянно меняется, можно вычислить мгновенную мощность. Она равна произведению силы тяги на мгновенную скорость: |
Мощность силы трения при равномерном движении по горизонтали |
Мощность силы трения отрицательна так же, как и работа. Это связано с тем, что угол между векторами силы трения и перемещения равен 180о (косинус равен –1). Учтем, что сила трения скольжения равна произведению силы нормальной реакции опоры на коэффициент трения: |
Пример №3. Машина равномерно поднимает груз массой 10 кг на высоту 20 м за 40 с. Чему равна ее мощность?
Коэффициент полезного действия
Не вся работа, совершаемая телами, может быть полезной. В реальном мире на тела действует несколько сил, препятствующих совершению работы другой силой. К примеру, чтобы переместить груз на некоторое расстояние, нужно совершить работу гораздо большую, чем можно получить при расчете по формулам выше.
Определения:
- Работа затраченная — полная работа силы, совершенной над телом (или телом).
- Работа полезная — часть полной работы силы, которая вызывает непосредственно перемещение тела.
- Коэффициент полезного действия (КПД) — процентное отношение полезной работы к работе затраченной. КПД обозначается буквой «эта» — η. Единицы измерения эта величина не имеет. Она показывает эффективность работы механизма или другой системы, совершающей работу, в процентах.
КПД определяется формулой:
Работа может определяться как произведение мощности на время, в течение которого совершалась работа:
A = Nt
Поэтому формулу для вычисления КПД можно записать в следующем виде:
Частые случаи определения КПД рассмотрим в таблице ниже:
Устройство |
Работа полезная и полная |
КПД |
| Неподвижный блок, рычаг |
Aполезн = mgh Асоверш. |
 |
| Наклонная плоскость |
Aполезн = mgh Асоверш. = Fl l — совершенный путь (длина наклонной плоскости). |
 |
Пример №4. Определите полезную мощность двигателя, если его КПД равен 40%, а его мощность по паспорту равна 100 кВт.
В данном случае необязательно переводить единицы измерения в СИ. Но в таком случае ответ мы тоже получим в кВт. Из этой формулы выразим полезную мощность:
Задание EF17557
Какую мощность развивает сила тяги трактора, перемещая прицеп со скоростью 18 км/ч, если она составляет 16,5 кН?
Ответ:
а) 916 Вт
б) 3300 Вт
в) 82500 Вт
г) 297000 Вт
Алгоритм решения
1.Записать исходные данные и перевести единицы измерения в СИ.
2.Записать формулу для расчета мощности.
3.Выполнить общее решение задачи.
4.Подставить известные данные и выполнить вычисления.
Решение
Запишем исходные данные:
• Сила тяги, перемещающая прицеп, равна: Fт = 16,5 кН.
• Скорость перемещения прицепа под действием силы тяги: v = 18 км/ч.
Переведем единицы измерения в СИ:
16,5 кН = 16,5∙103 Н
18 км/ч = 18000/3600 м/с = 5 м/с
Мощность равна отношению работы ко времени, в течение которого эта работа совершалась:
N=At
Но работа равна произведению силы, перемещения и косинуса угла между векторами силы и перемещения. В данном случае будем считать, что угол равен нулю, следовательно косинус — единице. Тогда работа равна:
A = Fs
Тогда мощность равна:
N=Fst=Fv=16,5·103·5=82500 (Вт)
Ответ: в
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17574
1) увеличится
2) уменьшится
3) не изменится
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
|
Время движения |
Ускорение |
Модуль работы силы трения |
Алгоритм решения
1.Установить наличие и характер зависимости кинематических характеристик движения от массы тела.
2.Вывести формулу для модуля работы силы трения.
3.Установить, как изменится модуль работы силы трения при уменьшении массы тела вдвое.
Решение
При скольжении с наклонной плоскости происходит равноускоренное движение. Положение тела в любой момент времени при таком движении можно определить с помощью кинематических уравнений:
x=xo+v0xt+axt22
y=yo+v0yt+ayt22
Из этих уравнений видно, что ускорение и время никак не зависят от массы тела. Следовательно, при уменьшении массы тела в 2 раза его время движения и ускорение не изменятся.
Чтобы выразить модуль работы силы трения, выберем такую систему отсчета, чтобы вектор силы трения был расположен вдоль оси Ox.Тогда сила трения будет равна:
Fтр = μmg
Известно, что работа определяется формулой:
A = Fs cosα
Тогда работа силы трения равна:
A = μmgs cosα
Вектор силы трения всегда направлен противоположно вектору перемещения. Поэтому косинус угла между ними равен –1. Но нас интересует только модуль работы. Поэтому будем считать, что он равен:
A = μmgs
Модуль работы силы трения и масса тела зависят прямо пропорционально. Следовательно, если массу тела уменьшить вдвое, то и модуль работы силы трения уменьшится вдвое.
Поэтому правильная последовательность цифр в ответе: 332.
Ответ: 332
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18646
В первой серии опытов брусок перемещают при помощи нити равномерно и прямолинейно вверх по наклонной плоскости. Во второй серии опытов на бруске закрепили груз, не меняя прочих условий.
Как изменятся при переходе от первой серии опытов ко второй сила натяжения нити и коэффициент трения между бруском и плоскостью?
Для каждой величины определите соответствующий характер её изменения:
1) увеличится
2) уменьшится
3) не изменится
Запишите в таблицу выбранные цифры для каждого ответа. Цифры в ответе могут повторяться.
| Сила натяжения нити | Коэффициент трения |
Алгоритм решения
- Определить, какая величина изменилась во второй серии опытов.
- Определить, как зависит от этой величины сила натяжения нити.
- Определить, как зависит от этой величины коэффициент трения.
Решение
Когда к бруску подвесили груз, увеличилась масса. Когда тело на нити перемещается вверх прямолинейно и равномерно, сила натяжения нити определяется модулем силы тяжести:
T = mg
Эта формула показывает, что сила натяжения нити и масса тела зависят прямо пропорционально. Если, добавив к бруску груз, масса увеличится, то сила натяжения нити тоже увеличится.
Коэффициент трения — это величина, которая зависит только от материалов и типа поверхности. Поэтому увеличение массы тела на него никак не повлияют.
Верная последовательность цифр в ответе: 13.
Ответ: 13
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18271
Определите коэффициент полезного действия атомной электростанции, расходующей за неделю уран-235 23592U массой 1,4 кг, если её мощность равна 38 МВт. При делении одного ядра урана-235 выделяется энергия 200 МэВ.
Алгоритм решения
1.Записать исходные данные и перевести их в СИ.
2.Записать формулу для определения КПД атомной электростанции.
3.Решить задачу в общем виде.
4.Подставить известные данные и вычислить искомую величину.
5.Массовое число: A = 235.
6.Зарядовое число: Z = 92.
Решение
Запишем исходные данные:
• Энергия, выделяемая при делении одного ядра урана-235: Q0 = 200 МэВ.
• Масса урана-235: m = 1,4 кг.
• Время, в течение которого происходит деление: t = 1 неделя.
• Мощность атомной электростанции: N = 38 МВт.
Переведем все единицы измерения в СИ:
1 эВ = 1,6∙10–19 Дж
200 МэВ = 200∙106∙1,6∙10–19 Дж = 320∙10–13 Дж
1 неделя = 7∙24∙60∙60 с = 604,8∙103 с
38 МВт = 38∙106 Вт
КПД атомной электростанции есть отношение полезной работы к выделенной за это же время энергии:
η=AполезнQ100%
Полезную работу мы можем вычислить по формуле:
A=Nt
Выделенное количество теплоты мы можем рассчитать, вычислив количество атомов, содержащихся в 1,4 кг урана-235 и умножив их на энергию, выделяемую при делении одного такого атома.
Количество атомов равно произведению количество молей на постоянную Авогадро:
Nкол.атомов = νNA
Количество молей равно отношения массы вещества к его молярной массе, следовательно:
Молярная масса численно равна массовому числу в граммах на моль. Следовательно:
M = A (г/моль) = A∙10–3 (кг/моль)
Отсюда количество атомов равно:
Энергия, выделенная всеми атомами, равна:
Теперь можем вычислить КПД:
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 12k
Все формулы работы
A = Fs
A = Fh
А = Nt
А = mhg
A = Q
A = UIt
Ап = cm (t2 – t1)
Aп = ηUIt
Ап = ηАз
Ап
Аз = ——
η
A – работа, Ап – полезная работа; Аз – затраченная работа; F – сила; s – пройденный путь; N – мощность; m – масса; h – высота; g – ускорение свободного падения, равное 9,8 Н/кг; Q – теплота; I – сила тока; t – время, в течение которого совершалась работа; c – удельная теплоемкость (выясняется по таблице); t2 и t1 – конечная и начальная температуры; η – коэффициент полезного действия, U – напряжение.
Единица работы – джоуль (Дж).
За единицу работы принимают работу, совершаемую силой в 1 Н, на пути, равном 1 м:
1 Дж = 1 Н · 1 м.
1 кДж = 1000 Дж; 1 Дж = 0,001 кДж
Механическая работа
- Зависимость механической работы от величины приложенной силы
- Зависимость механической работы от величины перемещения
- Определение механической работы
- Единицы измерения механической работы
- Задачи
п.1. Зависимость механической работы от величины приложенной силы
Приложенная к телу сила приводит его в движение и сообщает ему ускорение. В результате действия силы тело перемещается. В таком случае говорят, что сила совершила работу по перемещению тела.
Допустим, мы перемещаем груз (одну коробку) на расстояние (s_1=10 text{м}) по горизонтальной плоскости, действуя на него силой (F_1=100 text{Н}).
Пусть масса груза увеличилась вдвое (мы положили вторую коробку сверху на первую). Теперь для перемещения необходима сила (F_2=200 text{Н}). При перемещении на то же расстояние (s_2=s_1=10 text{м}) мы совершим в два раза большую работу. По существу, во втором случае мы перемещаем за один раз две коробки, что равносильно перемещению по одной коробке за два раза.
Следовательно, чем больше приложенная сила, тем большую работу она совершает: работа прямо пропорциональна величине приложенной силы.
п.2. Зависимость механической работы от величины перемещения
Теперь рассмотрим зависимость работы от величины перемещения.
Пусть вначале мы перемещаем груз (одну коробку) на расстояние (s_1=5 text{м}) по горизонтальной плоскости, действуя на него силой (F_1=100 text{Н}).
А затем перемещаем тот же груз с той же силой на расстояние (s_2=10 text{м}).
Во втором случае мы совершим вдвое большую работу.
Чем больше величина перемещения под действием силы, тем большую работу совершает эта сила: работа прямо пропорциональна перемещению в направлении действующей силы.
Уточнение про перемещение в направлении действующей силы очень важно.
И сила и перемещение являются векторными величинами: направление для их описания так же существенно, как и величина.
Работа является величиной скалярной. От взаимного направления силы и перемещения зависит не только величина, но и знак работы: она может быть положительной, равной нулю или отрицательной.
п.3. Определение механической работы
Механическая работа – скалярная величина, равная произведению силы на перемещение в направлении действия этой силы.
В этом курсе мы ограничимся тремя случаями взаимной ориентации векторов силы и перемещения:
- Если направления векторов силы и перемещения совпадают, то работа положительна и равна произведению модуля силы на модуль перемещения: $$ A=Fs, overrightarrow{F}uparrowuparrowoverrightarrow{s} $$
- Если направления векторов силы и перемещения противоположны, то работа отрицательна и равна произведению модуля силы на модуль перемещения, взятому со знаком «минус»: $$ A=-Fs, overrightarrow{F}uparrowdownarrowoverrightarrow{s} $$
- Если направления векторов силы и перемещения перпендикулярны, то работа равна 0. $$ A=0, overrightarrow{F}perpoverrightarrow{s} $$
Остальные случаи взаимной ориентации векторов будут рассмотрены в курсе физики для 9 класса.
Пример определения работы для трех базовых случаев взаимного расположения векторов силы и перемещения
Рассмотрим перемещение деревянного бруска по поверхности стола.
Брусок перемещается в направлении приложенной силы тяги (overrightarrow{F}). Направления перемещения и силы тяги совпадают, эта сила совершает положительную работу: $$ A_text{тяги}=Fs, overrightarrow{F}uparrowuparrowoverrightarrow{s} $$
Сила трения направлена противоположно перемещению; она совершает отрицательную работу: $$ A_text{тр}=-Fs, overrightarrow{F}_text{тр}uparrowdownarrowoverrightarrow{s} $$
Сила тяжести направлена перпендикулярно перемещению; её работа равна нулю: $$ A_text{тяж}=0, moverrightarrow{g}perpoverrightarrow{s} $$
п.4. Единицы измерения механической работы
В системе СИ (см. §2 данного справочника) сила измеряется в ньютонах, перемещение – в метрах. А для измерения работы используется «джоуль».
Единицей работы в системе СИ является джоуль (1 Дж) – работа силы 1Н по перемещению тела на 1 м в направлении действия силы: $$ 1 text{Дж}=1 text{Н}cdot 1 text{м} $$
п.5. Задачи
Задача 1. Груз весом 50 Н равномерно подняли, совершив работу 400 Дж.
На какую высоту подняли груз?
Дано:
(P=r0 text{Н})
(A=400 text{Дж})
__________________
(h-?)
Груз перемещается равномерно, следовательно, равнодействующая веса и силы тяги равна нулю begin{gather*} overrightarrow{P}+overrightarrow{F}=0 Rightarrow overrightarrow{F}=-overrightarrow{P} end{gather*} Cила тяги равна весу по величине и противоположна по направлению. begin{gather*} F=P end{gather*} Сила тяги и перемещение направлены в одну сторону – вверх. Работа силы тяги begin{gather*} A=Fh end{gather*} Высота равна begin{gather*} h=frac AF=frac AP end{gather*} Получаем begin{gather*} h=frac{400}{50}=8 (text{м}) end{gather*} Ответ: 8 м
Задача 2. С плотины гидроэлектростанции каждую секунду падает 1800 м3 воды. Какую работу совершает каждую секунду действующая на эту воду сила тяжести, если высота плотины 25 м?
Дано:
(V=1800 text{м}^3)
(h=25 text{м})
(rho=1000 text{кг/м}^3)
(gapprox 10 text{м/с}^2)
__________________
(A-?)
Масса падающей воды begin{gather*} m=rho V. end{gather*} Сила тяжести $$ F=mg=rho Vg. $$ Работа силы тяжести begin{gather*} A=Fh=rho V gh. end{gather*} Получаем: $$ A=1000cdot 1800cdot 10cdot 25=450cdot 10^6 (text{Дж})=450 (text{МДж}) $$ Ответ: 450 МДж
Задача 3. Подъемный кран в течение 50 секунд равномерно поднимал груз массой 2 т, совершив при этом работу 360 кДж. С какой скоростью двигался груз?
Дано:
(t=50 text{с})
(m=2 text{т}=2000 text{кг})
(A=360 text{кДж}=3,6cdot 10^5 text{Дж})
(gapprox 10 text{м/с}^2)
__________________
(v-?)
Груз перемещается равномерно, следовательно, равнодействующая веса и силы тяги равна нулю begin{gather*} overrightarrow{P}+overrightarrow{F}=0 Rightarrow overrightarrow{F}=-overrightarrow{P} end{gather*} Cила тяги равна весу по величине и противоположна по направлению: begin{gather*} F=P=mg end{gather*} Сила тяги и перемещение направлены в одну сторону – вверх. Работа силы тяги: begin{gather*} A=Fh end{gather*} Высота равна: begin{gather*} h=frac AF=frac AP=frac{A}{mg} end{gather*} Подъем происходит равномерно, скорость подъема: begin{gather*} v=frac ht=frac{A}{mgt} end{gather*} Получаем: begin{gather*} v=frac{3,6cdot 10^5}{2cdot 10^3cdot 10cdot 50}=0,36 (text{м/с}) end{gather*} Ответ: 0,36 м/с
Задача 4*. Со дна озера на поверхность воды подняли камень объемом 8 дм3.
Глубина озера 10 м. Определите плотность камня, если при его подъеме лебедка совершила работу 1200 Дж. Сопротивлением воды при подъеме можно пренебречь.
Дано:
(V=8 text{дм}^3=8cdot 10^{-3} text{м}^3)
(h=10 text{м})
(rho_text{в}=1000 text{кг/м}^3)
(A=1200 text{Дж})
__________________
(rho_text{к}-?)
На камень действуют три силы: сила тяги (overrightarrow{F}) сила Архимеда (overrightarrow{F}_a), сила тяжести (moverrightarrow{g}).
Сила тяги и сила Архимеда в сумме уравновешивают силу тяжести: begin{gather*} F+F_a=mg end{gather*} Сила Архимеда: begin{gather*} F_a=rho_text{в}Vg end{gather*} Работа силы тяги begin{gather*} A=Fh end{gather*} Сила тяги: begin{gather*} F=frac Ah end{gather*} Масса камня begin{gather*} m=rho_{text{к}}V end{gather*} Подставляем: begin{gather*} frac Ah+rho_{text{в}}Vg=rho_{text{к}}Vg end{gather*} Плотность камня: begin{gather*} rho_{text{к}}=frac{A}{hVg}+rho_{text{в}} end{gather*} Подставляем: begin{gather*} rho_{text{к}}=frac{1200}{10cdot 8cdot 10^{-3}cdot 10}+1000=2500 text{кг/м}^3 end{gather*} Ответ: 2500 кг/м3
Задача 5. Лошадь везет сани массой 250 кг с постоянной скоростью 2 м/с.
Найдите коэффициент трения между полозьями и дорогой, если за 1 ч работа по перемещению саней составила 3,3 МДж?
Дано:
(m=250 text{кг})
(v=2 text{м/с})
(t=1 text{ч}=3600 text{с})
(A=3,6cdot 10^6 text{Дж})
__________________
(mu-?)
На сани действуют четыре силы: по вертикали – сила тяжести (mg) и сила реакции опоры (N), по горизонтали – сила тяги (F) и сила трения (F_text{тр}), причем begin{gather*} N=mg, F=F_text{тр} end{gather*} Работа силы тяги begin{gather*} A=Fs=Fcdot vtRightarrow F=frac{A}{vt} end{gather*} Сила трения begin{gather*} F_text{тр}=mu N=mu mg end{gather*} Получаем begin{gather*} frac{A}{Vt}=mu mgRightarrow mu=frac{A}{vtcdot mg} end{gather*} Подставляем begin{gather*} mu=frac{3,6cdot 10^6}{2cdot 3600cdot 250cdot 10}=0,2 end{gather*} Ответ: 0,2
Задача 6*. Какую работу совершает сила давления газов при выталкивании ядра из пушки, если длина ствола 1,6 м, радиус ядра 10 см, а среднее давление в стволе во время выстрела в 2000 раз превышает атмосферное давление? Ответ округлите до десятых долей мегаджоуля.
Дано:
(s=1,6 text{м})
(R=10 text{см}=0,1 text{м})
(p=2000p_0)
(p_0=101300 text{Па})
__________________
(A-?)
Сила давления газов равна begin{gather*} F=pS, end{gather*} где (S) — площадь поперечного сечения ядра (S=pi R^2).
Работа газов begin{gather*} A=Fs=pcdot pi R^2cdot s end{gather*} Получаем begin{gather*} A=2000cdot 101300cdot picdot 0,1^2cdot 1,6approx 10183786 text{Дж}approx 10,2 text{МДж} end{gather*} Ответ: ≈10,2 МДж