Адиабатическое сжатие это термодинамический процесс, при котором внутренняя энергия системы увеличивается из-за повышения температуры.
Адиабатическое сжатие характеризуется отсутствием передачи тепла между системой и окружающей средой. Повышение температуры во время адиабатического сжатия приводит к увеличению давления, которое обычно намного сильнее, чем скорость уменьшения объема.
Адиабатический процесс можно определить выражением:
PVꝩ = Постоянный
Где,
P = Давление в системе
V: объем системы
ꝩ = Отношение удельной теплоемкости газа (Cp / Cv)
Здесь Cp — удельная теплоемкость при постоянном давлении, а Cv — удельная теплоемкость при постоянном объеме. В приведенном выше уравнении считается, что система идеально изолирована от окружающей среды, так что dQ = 0, или нет передачи тепла с окружающей средой. Другое предположение приведенных выше выражений состоит в том, что газ должен быть идеальным газом (коэффициент сжимаемости = 1).
На практике идеальное поведение демонстрирует небольшое количество газов или состав газов. Кроме того, всегда есть потери тепла в окружающую среду, когда работа фотоэлектрических систем выполняется системой. Однако для всех практических целей поведение большинства газов близко к идеальному при давление и температура выше их точки кипения. В этих условиях столкновения между газами абсолютно упругие, а межмолекулярные силы между сталкивающимися атомами почти отсутствуют.

Изображение |: упругое столкновение
источник: https://www.nuclear-power.com/nuclear-engineering/thermodynamics/ideal-gas-law/what-is-ideal-gas/
Еще один практический пример адиабатического процесса — газовая турбина операции, где процесс изменения очень рейд. В этих процессах потери тепла происходят, но их количество довольно мало по сравнению с теплом, передаваемым в процессе, что делает их незначительными. Другой пример адиабатический процесс — такты сжатия и расширения двигателя внутреннего сгорания.

PV диаграмма тактов в двигателе внутреннего сгорания
Image Source: https://engineeringinsider.org/adiabatic-process-types/
Что такое адиабатическое сжатие?
В термодинамике адиабатический процесс характеризуется dQ = 0, где Q — сердце, перенесенное с окружающим.
Адиабатическое сжатие — это процесс, при котором работа фотоэлектрической системы отрицательна, что приводит к повышению температуры системы. Это повышение температуры увеличивает внутреннюю энергию системы.
Адиабатическое сжатие предполагает идеальную изоляцию, что чисто теоретически. Однако инженеры могут безопасно сделать адиабатическое допущение для всех практических целей в процессах, которые достаточно хорошо изолированы или которые являются очень быстрыми.
Адиабатическое сжатие, как это работает?
Адиабатическое сжатие работает по тем же принципам, что и первый закон термодинамики.
Первый закон термодинамики гласит, что
dQ = dU + dW
In адиабатическое сжатие, поскольку теплопередача с окружающей средой равна нулю, приведенное выше уравнение можно записать как:
dU = -PdV
Из сказанного следует, что увеличение внутренней энергии соответствует уменьшению объема. На увеличение внутренней энергии указывает повышение температуры системы.

PV Схема адиабатического процесса
источник: https://engineeringinsider.org/adiabatic-process-types/
Всегда ли сжатие адиабатично?
Сжатие осуществляется для сжимаемых жидкостей, которые в основном представляют собой газ, и это происходит по различным термодинамическим путям.
Процесс сжатия газа термодинамически может быть трех типов: — изотермическое, адиабатическое и политропическое сжатие. Все эти различные типы сжатия могут привести к различным конечным условиям при одинаковом объеме выполненной работы.
Изотермическое сжатие: как следует из названия, этот тип сжатия происходит при постоянной температуре. Это достигается за счет обеспечения охлаждающей жидкости над корпусом компрессора и / или межступенчатого охлаждения. Однако на практике добиться полного изотермического сжатия очень сложно. Сжатие, близкое к изотермическому, может быть достигнуто, если процесс сжатия протекает в очень медленном темпе с достаточным временем для отвода тепла, образующегося в процессе. Изотермическое сжатие дается выражением
PV = постоянный
Адиабатическое сжатие: этот тип сжатия требует, чтобы сжатие осуществлялось без потери или увеличения тепла из окружающей среды. Для этого требуется идеально изолированная система. Другой способ добиться адиабатическое сжатие заключается в том, чтобы производить сжатие в очень быстром темпе, чтобы не было времени для передачи тепла от системы к окружающей среде. Адиабатическое сжатие выражается выражением:
PVꝩ= константа, где ꝩ — отношение удельной теплоты сжимаемого газа.
Политропное сжатие: Политропное сжатие определяет фактические процессы сжатия, происходящие в реальных системах сжатия, например, в газовом компрессоре. А процесс политропного сжатия задается выражением:
PVn = Константа, где n изменяется от 1 до 1.4.
Формула адиабатического сжатия
Формула адиабатического сжатия выводится из первого закона термодинамики с учетом отсутствия передачи тепла в систему и из системы.
Формула для адиабатического сжатия может быть выражена в различных формах, например, в форме PV, в форме TV и в форме PT, где P, V и T — это давление, объем и температура соответственно.
Адиабатическое сжатие в форме давления и температуры определяется как:
P1-Ꝩ Tꝩ = Постоянный
Адиабатическое сжатие в объемно-температурной форме:
TVꝩ-1= Постоянный
Адиабатическое сжатие в форме давления и объема определяется как:
PVꝩ= Постоянный
Как рассчитать адиабатическое сжатие?
Адиабатическое сжатие можно рассчитать по формуле PVꝩ= Константа.
Поршень, сжимающий газ в цилиндре, назовем адиабатическим процессом, когда передача тепла в окружающую среду равна нулю. В таком случае, если известны начальные условия (P1 и V1), а также отношение удельной теплоемкости газа (), можно получить любое из конечных условий (P2, V2), если оно задано. Таким образом, формула принимает следующий вид:
P1V1ꝩ= P2V2ꝩ
Что вызывает адиабатическое сжатие (не имеет значения)
Работа, проделанная при адиабатическом сжатии
Работа, проделанная в адиабатическом процессе, может быть получена из формулы для адиабатического процесса
PVꝩ= Константа (K). Эту формулу можно переписать как P = KV—
Чтобы рассчитать работу, совершенную в адиабатический процесс , будем считать, что система сжата от начального положения P1, V1 и T1 до конечного положения P2, V2 и T2. Совершенная работа определяется
Выполненная работа (Вт) = Сила x смещение
W = Fdx
W = PAdx
W = P (Adx)
W = PdV
Чтобы рассчитать работу, проделанную во время сжатия от V1 до V2, PdV необходимо интегрировать с пределами V1 и V2.
Или W =
Или W =dV Где P = KV—
Это можно представить как работа, выполненная в адиабатическом процессе.
Интегрируя дальше, мы получаем окончательное выражение для проделанной работы как
W=1/(1−γ) {P2V2−P1V1}
Какая работа выполняется в адиабатическом процессе
Адиабатический процесс может быть адиабатическим сжатием или адиабатическим расширением.
В случае при адиабатическом сжатии работа совершается окружающей средой над системой и при адиабатическом расширении работа совершается системой над окружающей средой. Работа, совершаемая в адиабатическом процессе, аналогична работе, совершаемой при адиабатическом сжатии или расширении.
Пример адиабатический расширение – это подъем горячего воздуха в атмосферу, который адиабатически расширяется из-за более низкого атмосферного давления и в результате остывает. В этом случае работа совершается поднимающимся горячим воздухом, а работа совершается системой.
Отрицательная ли работа при адиабатическом сжатии?
Да, работа, совершаемая системой при адиабатическом сжатии отрицательно.
Адиабатическое сжатие происходит с увеличением внутренней энергии системы. Мы знаем из первого закона термодинамика что, поскольку dQ при адиабатическом сжатии равно нулю,
dU + dW = 0
или dU = -dW
dU и dW имеют отрицательное отношение друг к другу. Таким образом, поскольку изменение внутренней энергии положительное, проделанная работа отрицательна.
Связь можно также подтвердить тем фактом, что при адиабатическом сжатии внутренняя энергия поднимается, работа над системой совершается окружающей средой, следовательно, работа, совершаемая системой над окружающей средой, отрицательна.
Напротив, работа, совершаемая системой над окружающей средой при адиабатическом расширении положительно.
Как вы рассчитываете работу, проделанную в адиабатическом процессе?
Адиабатический процесс может быть достигнут, если расширение или сжатие газа осуществляется в идеально изолированной системе или происходит так быстро, что передача тепла в окружающую среду незначительна.
Математически нет никакой разницы между адиабатическим расширением и адиабатическим сжатием, и, следовательно, они следуют одним и тем же формулам и выводам.
Таким образом, все приведенные выше формулы для адиабатического сжатия справедливы для любого адиабатического процесса.
Обратимо ли адиабатическое сжатие?
Адиабатическое сжатие обратимо, если нет изменения энтропии
Процесс называется обратимым, если он изоэнтропический, либо энтропия системы не изменяется, либо dS=0. Адиабатическое сжатие – это такое сжатие, при котором не происходит изменения теплопередача с окрестностями. Чтобы адиабатическое сжатие было обратимым, процесс сжатия должен быть без трения.
An пример обратимой адиабаты сжатие, которое также называют изоэнтропическим сжатием, можно найти в газовой турбине или современных реактивных двигателях. Этот газ турбины работают по циклу Брайтона как показано ниже.

На приведенном выше рисунке идеал Цикл Брайтона состоит из четырех термодинамических процессов.
Этап 1-> этап 2: изоэнтропическое сжатие
Этап 2-> этап 3: Изобарический нагрев
Этап 3-> этап 4: Изоэнтропийное расширение
Первый закон термодинамики
-
Темы кодификатора ЕГЭ: работа в термодинамике, первый закон термодинамики, адиабатный процесс.
-
Работа газа в изобарном процессе
-
Работа газа в произвольном процессе
-
Работа, совершаемая над газом
-
Применение первого закона термодинамики к изопроцессам
-
Адиабатный процесс
Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: работа в термодинамике, первый закон термодинамики, адиабатный процесс.
Начнём с обсуждения работы газа.
Газ, находящийся в сосуде под поршнем, действует на поршень с силой , где
— давление газа,
— площадь поршня. Если при этом поршень перемещается, то газ совершает работу.
При расширении газа эта работа будет положительной (сила давления газа и перемещение поршня направлены в одну сторону). При сжатии работа газа отрицательна (сила давления газа и перемещение поршня направлены в противоположные стороны).
к оглавлению ▴
Работа газа в изобарном процессе
Предположим, что газ расширяется при постоянном давлении . Тогда сила
, с которой газ действует на поршень, также постоянна. Пусть поршень переместился на расстояние
(рис. 1).
Рис. 1.
Работа газа равна:
Но — изменение объёма газа. Поэтому для работы газа при изобарном расширении мы получаем формулу:
(1)
Если и
— начальный и конечный объём газа, то для работы газа имеем:
. Изобразив данный процесс на
-диаграмме, мы видим, что работа газа равна площади прямоугольника под графиком нашего процесса (рис. 2).
Рис. 2. Работа газа как площадь
Пусть теперь газ изобарно сжимается от объёма до объёма
. С помощью аналогичных рассуждений приходим к формуле:
Но , и снова получается формула (1).
Работа газа опять-таки будет равна площади под графиком процесса на -диаграмме, но теперь со знаком минус.
Итак, формула выражает работу газа при постоянном давлении — как в процессе расширения газа, так и в процессе сжатия.
к оглавлению ▴
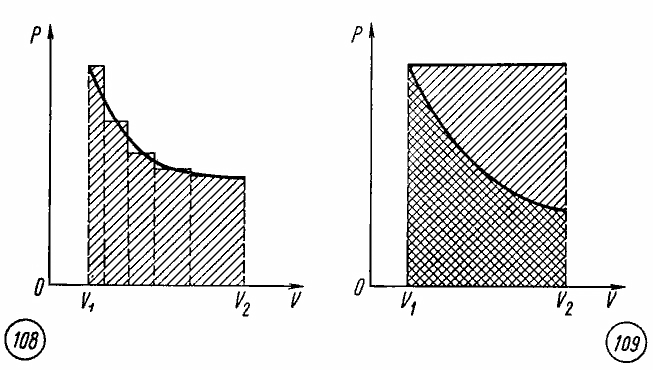
Работа газа в произвольном процессе
Геометрическая интерпретация работы газа (как площади под графиком процесса на -диаграмме) сохраняется и в общем случае неизобарного процесса.
Действительно, рассмотрим малое изменение объёма газа — настолько малое, что давление
будет оставаться приблизительно постоянным. Газ совершит малую работу
. Тогда работа
газа во всём процессе найдётся суммированием этих малых работ:
Но данный интеграл как раз и является площадью криволинейной трапеции (рис. 3):
Рис. 3. Работа газа как площадь
к оглавлению ▴
Работа, совершаемая над газом
Наряду с работой , которую совершает газ по передвижению поршня, рассматривают также работу
, которую поршень совершает над газом.
Если газ действует на поршень с силой , то по третьему закону Ньютона поршень действует на газ с силой
, равной силе
по модулю и противоположной по направлению:
(рис. 4).
Рис. 4. Внешняя сила , действующая на газ
Следовательно, работа поршня равна по модулю и противоположна по знаку работе газа:
Так, в процессе расширения газ совершает положительную работу ; при этом работа, совершаемая над газом, отрицательна
. Наоборот, при сжатии работа газа отрицательна
, а работа, совершаемая поршнем над газом, положительна
0 right )’ class=’tex’ alt=’left ( {A}’ > 0 right )’ />.
Будьте внимательны: если в задаче просят найти работу, совершённую над газом, то имеется в виду работа .
Как мы знаем, существует лишь два способа изменения внутренней энергии тела: теплопередача и совершение работы.
Опыт показывает, что эти способы независимы — в том смысле, что их результаты складываются. Если телу в процессе теплообмена передано количество теплоты , и если в то же время над телом совершена работа
, то изменение внутренней энергии тела будет равно:
(2)
Нас больше всего интересует случай, когда тело является газом. Тогда (где
, как всегда, есть работа самого газа). Формула (2) принимает вид:
, или
(3)
Соотношение (3) называется первым законом термодинамики. Смысл его прост: количество теплоты, переданное газу, идёт на изменение внутренней энергии газа и на совершение газом работы.
Напомним, что величина может быть и отрицательной: в таком случае тепло отводится от газа. Но первый закон термодинамики остаётся справедливым в любом случае. Он является одним из фундаментальных физических законов и находит подтверждение в многочисленных явлениях и экспериментах.
к оглавлению ▴
Применение первого закона термодинамики к изопроцессам
Напомним, что в изопроцессе остаётся неизменным значение некоторой величины, характеризующей состояние газа — температуры, объёма или давления. Для каждого вида изопроцессов запись первого закона термодинамики упрощается.
1. Изотермический процесс, .
Внутренняя энергия идеального газа зависит только от его температуры. Если температура газа не меняется, то не меняется и внутренняя энергия: . Тогда формула (3) даёт:
Всё подведённое к газу тепло идёт на совершение газом работы.
2. Изохорный процесс, .
Если объём газа остаётся постоянным, то поршень не перемещается, и потому работа газа равна нулю: . Тогда первый закон термодинамики даёт:
Всё тепло, переданное газу, идёт на изменение его внутренней энергии.
3. Изобарный процесс, .
Подведённое к газу тепло идёт как на изменение внутренней энергии, так и на совершение работы (для которой справедлива формула (1)). Имеем:
к оглавлению ▴
Адиабатный процесс
Процесс называется адиабатным, если он идёт без теплообмена с окружающими телами.
Адиабатный процесс совершается газом, находящимся в теплоизолированном сосуде. Такой сосуд препятствует всем видам теплопередачи: теплопроводности, конвекции, излучению. Пример теплоизолированного сосуда — термос.
Приблизительно адиабатным будет всякий процесс, протекающий достаточно быстро: в течение процесса теплообмен просто не успевает произойти.
При адиабатном процессе . Из первого закона термодинамики получаем:
, или
.
В процессе адиабатного расширения газ совершает положительную работу, поэтому (работа совершается за счёт убыли внутренней энергии). Следовательно, газ охлаждается. Если заставить газ совершить достаточно большую работу, охладить его можно весьма сильно. Именно на этом основаны методы сжижения газов.
Наоборот, в процессе адиабатного сжатия будет , поэтому
: газ нагревается. Адиабатное нагревание воздуха используется в дизельных двигателях для воспламенения топлива.
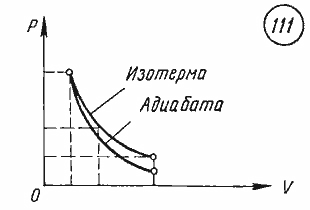
Кривая, изображающая ход адиабатного процесса, называется адиабатой. Интересно сравнить ход адиабаты и изотермы на -диаграмме (рис. 5).
Рис. 5. Сравнительный ход изотермы и адиабаты
В обоих процессах давление убывает с увеличением объёма, но в адиабатном процессе убывание идёт быстрее. Почему?
При изотермическом расширении давление падает потому, что уменьшается концентрация частиц газа, в результате чего удары частиц по стенкам сосуда становятся реже. Однако интенсивность этих ударов остаётся прежней: ведь температура газа не меняется — значит, не меняется и средняя кинетическая энергия его частиц.
А при адиабатном расширении, наряду с уменьшением концентрации частиц, падает также и температура газа. Удары частиц становятся не только более редкими, но и более слабыми. Вот почему адиабата убывает быстрее изотермы.
Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Первый закон термодинамики» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.
Публикация обновлена:
08.05.2023
Работа расширения или сжатия газа
Одним
из основных термодинамических процессов,
совершающихся в большинстве тепловых
машин, является процесс расширения газа
с совершением работы. Легко определить
работу, совершаемую при изобарном
расширении газа.
Если
при изобарном расширении газа от объема
V1
до объема V2
происходит перемещение поршня в цилиндре
на расстояние l
(рис. 7.3), то работа A’,
совершенная газом, равна
,
(7.27)
где
p
— давление газа,
—
изменение его объема.
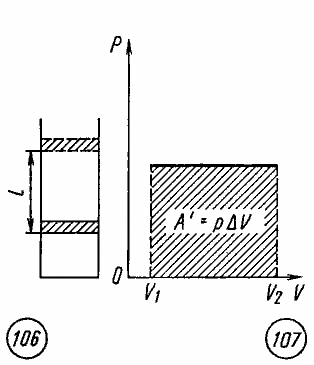
Рис
7.3 Рис 7.4
Как
видно из рисунка 7.4, при изображении
изобарного процесса расширения газа в
координатных осях p
, V
площадь фигуры, ограниченной графиком
процесса, координатами V1
и V2,
осью абсцисс, пропорциональна работе
газа A’.
Работа
при произвольном процессе расширения
газа.
Произвольный процесс расширения газа
от объема V1
до объема V2
можно представить как совокупность
чередующихся изобарных и изохорных
процессов.
При
изохорных процессах работа равна нулю,
так как поршень в цилиндре не перемещается.
Работа при изобарных процессах
пропорциональна площади фигуры на
диаграмме p,
V
под соответствующим участком изобары
(рис. 7.5).
Рис.
7.5
Рис. 7.6
Следовательно,
работа при произвольном процессе
расширения газа прямо пропорциональна
площади фигуры под соответствующим
участком графика процесса на диаграмме
p,
V.
Работа
при изотермическом расширении газа.
Сравнивая площади фигур под участками
изотермы и изобары (рис. 7.6), можно сделать
вывод, что расширение газа от объема V1
до объема V2
при одинаковом начальном значении
давления газа сопровождается в случае
изобарного расширения совершением
большей работы.
Работа
при сжатии газа.
При расширении газа направление вектора
силы давления газа совпадает с направлением
вектора перемещения, поэтому работа
A’,
совершенная газом, положительна (A’
> 0), а работа А
внешних сил отрицательна: A
= —A’
< 0.
При
сжатии газа направление вектора внешней
силы совпадает с направлением перемещения,
поэтому работа А
внешних сил положительна (A
> 0), а работа A’,
совершенная газом, отрицательна (A’
< 0).
Адиабатный
процесс.
Кроме изобарного, изохорного и
изотермического процессов, в термодинамике
часто рассматриваются адиабатные
процессы.
Адиабатным
процессом
называется процесс, происходящий в
термодинамической системе при отсутствии
теплообмена с окружающими телами, т. е.
при условии Q
= 0.
Отсутствие
теплообмена с окружающей средой может
быть обеспечено хорошей теплоизоляцией
газа. Быстрые процессы расширения или
сжатия газа могут быть близкими к
адиабатному и при отсутствии теплоизоляции,
если время, за которое происходит
изменение объема газа, значительно
меньше времени, необходимого для
установления теплового равновесия газа
с окружающими телами.
Примерами
адиабатных процессов могут служить
процессы сжатия воздуха в цилиндре
воздушного огнива, в цилиндре двигателя
внутреннего сгорания. В соответствии
с первым законом термодинамики, при
адиабатном сжатии изменение внутренней
энергии газа
равно
работе внешних сил А:
(7.28)
Так
как работа внешних сил при сжатии
положительна, внутренняя энергия газа
при адиабатном сжатии увеличивается,
его температура повышается.
При
адиабатном расширении газ совершает
работу A’
за счет уменьшения своей внутренней
энергии:
,
(7.29)
поэтому
температура газа при адиабатном
расширении понижается. Это можно
обнаружить в следующем опыте. Если в
бутылку, содержащую насыщенный водяной
пар, накачивать с помощью насоса воздух,
то пробка вылетает (рис. 7.7).
Рис.
7.7
Работа
A’
по выталкиванию пробки совершается
воздухом за счет уменьшения его внутренней
энергии, так как расширение воздуха
происходит за очень короткое время и
теплообмен с окружающей средой не
успевает произойти. Образование капель
тумана доказывает, что при адиабатном
расширении воздуха его температура
понизилась и опустилась ниже точки
росы.
График
адиабатного процесса.
Поскольку при адиабатном сжатии
температура газа повышается, то давление
газа с уменьшением объема растет быстрее,
чем при изотермическом процессе.
Понижение температуры газа при адиабатном
расширении приводит к тому, что давление
газа убывает быстрее, чем при изотермическом
расширении.
График
адиабатного процесса в координатных
осях p,
V
представлен на рисунке 1.8. На том же
рисунке для сравнения приведен график
изотермического процесса.
Рис.
7.8
Вну́тренняя
эне́ргия
тела (обозначается как E
или U) —
полная энергия этого тела за вычетом
кинетической
энергии
тела как целого и потенциальной
энергии
тела во внешнем поле сил. Следовательно,
внутренняя энергия складывается из
кинетической энергии хаотического
движения молекул,
потенциальной энергии взаимодействия
между ними и внутримолекулярной энергии.
Внутренняя
энергия является однозначной функцией
состояния системы. Это означает, что
всякий раз, когда система оказывается
в данном состоянии, её внутренняя энергия
принимает присущее этому состоянию
значение, независимо от предыстории
системы. Следовательно, изменение
внутренней энергии при переходе из
одного состояния в другое будет всегда
равно разности между ее значениями в
конечном и начальном состояниях,
независимо от пути, по которому совершался
переход.
Внутреннюю
энергию тела нельзя измерить напрямую.
Можно определить только изменение
внутренней энергии:
где
—подведённая
к телу теплота,
измеренная в джоулях
—работа,
совершаемая телом против внешних сил,
измеренная в джоулях
Эта
формула является математическим
выражением первого
начала термодинамики
Для
квазистатических
процессов
выполняется следующее соотношение:
где
—температура,
измеренная в кельвинах
—энтропия,
измеренная в джоулях/кельвин
—давление,
измеренное в паскалях
—химический
потенциал
—количество
частиц в системе
Идеальные
газы
Согласно
закону Джоуля, выведенному эмпирически,
внутренняя энергия идеального
газа
не зависит от давления или объёма. Исходя
из этого факта, можно получить выражение
для изменения внутренней энергии
идеального газа. По определению молярной
теплоёмкости
при постоянном объёме,
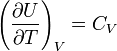
Так как внутренняя энергия идеального
газа является функцией только от
температуры, то

(7.30)
Эта
же формула верна и для вычисления
изменения внутренней энергии любого
тела, но только в процессах при постоянном
объёме (изохорных
процессах);
в общем случае CV
(T,V)
является функцией и температуры, и
объёма.
Если
пренебречь изменением молярной
теплоёмкости при изменении температуры,
получим:
ΔU
= νCVΔT,
(7.31)
где
ν — количеств о вещества, ΔT —
изменение температуры.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Адиабатический процесс и уравнения адиабаты для идеального газа. Пример задачи
Адиабатический переход между двумя состояниями в газах не относится к числу изопроцессов, тем не менее, он играет важную роль не только в различных технологических процессах, но и в природе. В данной статье рассмотрим, что представляет собой этот процесс, а также приведем уравнения адиабаты идеального газа.
Кратко об идеальном газе
Идеальным называется такой газ, в котором нет взаимодействий между его частицами, и их размеры равны нулю. В природе, конечно же, не существует идеальных на сто процентов газов, поскольку все они состоят из имеющих размеры молекул и атомов, которые взаимодействуют друг с другом всегда как минимум с помощью ван-дер-ваальсовых сил. Тем не менее, описанная модель часто выполняется с достаточной для решения практических задач точностью для многих реальных газов.

Главным уравнением идеального газа является закон Клапейрона-Менделеева. Он записывается в следующей форме:
Это уравнение устанавливает прямую пропорциональность между произведением давления P на объем V и количества вещества n на абсолютную температуру T. Величина R — газовая константа, которая играет роль коэффициента пропорциональности.
Что это адиабатический процесс?
Адиабатический процесс — это такой переход между состояниями газовой системы, при котором обмена энергией с внешней средой не происходит. При этом изменяются все три термодинамических характеристики системы (P, V, T), а количество вещества n остается постоянным.
Различают адиабатическое расширение и сжатие. Оба процесса происходят только за счет внутренней энергии системы. Так, в результате расширения давление и особенно температура системы сильно падают. Наоборот, адиабатическое сжатие приводит к положительному скачку температуры и давления.
Чтобы не происходил обмен теплом между окружающей средой и системой, последняя должна обладать теплоизолированными стенками. Кроме того, сокращение длительности протекания процесса значительно уменьшает тепловой поток от и к системе.
Уравнения Пуассона для адиабатического процесса
Первый закон термодинамики записывается в таком виде:
Иными словами, сообщенная системе теплота Q идет на выполнение системой работы A и на повышение ее энергии внутренней ΔU. Чтобы написать уравнение адиабаты, следует положить Q=0, что соответствует определению изучаемого процесса. Получаем:
При изохорном процессе в идеальном газе все тепло идет на повышение внутренней энергии. Этот факт позволяет записать равенство:
Где CV — изохорная теплоемкость. Работа A, в свою очередь, вычисляется так:
Где dV — малое изменение объема.
Помимо уравнения Клапейрона-Менделеева, для идеального газа справедливо следующее равенство:
Где CP — изобарная теплоемкость, которая всегда больше изохорной, так как она учитывает потери газа на расширение.
Анализируя записанные выше равенства и проводя интегрирование по температуре и объему, приходим к следующему уравнению адиабаты:
Здесь γ — это показатель адиабаты. Он равен отношению изобарной теплоемкости к изохорной. Это равенство называется уравнением Пуассона для процесса адиабатического. Применяя закон Клапейрона-Менделеева, можно записать еще два аналогичных выражения, только уже через параметры P-T и P-V:
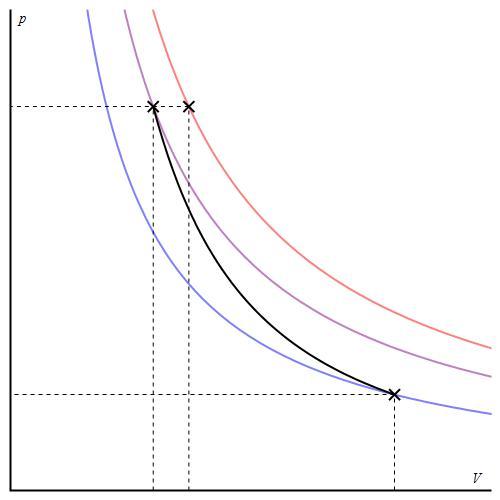
График адиабаты можно привести в различных осях. Ниже он показан в осях P-V.
Цветные линии на графике соответствуют изотермам, черная кривая — это адиабата. Как видно, адиабата ведет себя более резко, чем любая из изотерм. Этот факт просто объяснить: для изотермы давление меняется обратно пропорционально объему, для изобаты же давление изменяется быстрее, поскольку показатель γ>1 для любой газовой системы.
Пример задачи
В природе в горной местности, когда воздушная масса движется вверх по склону, то ее давление падает, она увеличивается в объеме и охлаждается. Этот адиабатический процесс приводит к снижению точки росы и к образованию жидких и твердых осадков.
Предлагается решить следующую задачу: в процессе подъема воздушной массы по склону горы давление упало на 30 % по сравнению с давлением у подножия. Чему стала равна ее температура, если у подножия она составляла 25 oC?
Для решения задачи следует использовать следующее уравнение адиабаты:
Его лучше записать в таком виде:
Если P1 принять за 1 атмосферу, то P2 будет равно 0,7 атмосферы. Для воздуха показатель адиабаты равен 1,4, поскольку его можно считать двухатомным идеальным газом. Значение температуры T1 равно 298,15 К. Подставляя все эти числа в выражение выше, получаем T2 = 269,26 К, что соответствует -3,9 oC.
2.4. Адиабатный процесс
Адиабатный процесс — это процесс, при котором не происходит теплообмена с внешней средой.
Физически это означает, что процесс протекает достаточно быстро и система не успевает обменяться теплотой с внешними телами. Однако коль скоро мы имеем дело с равновесными процессами, скорость адиабатного процесса не должна быть слишком уж велика. Примером таких процессов может служить распространение звуковых колебаний в упругой среде.
Выведем уравнение, описывающее адиабатный процесс. Ранее мы имели дело с самыми простыми уравнениями процессов
— для изотермического процесса;
— для изобарного процесса;
— для изохорного процесса.
Поскольку в адиабатном процессе dQ = 0, из первого начала термодинамики следует, что
C другой стороны,
Приравнивая эти выражения, находим
Умножая уравнение (2.28) на V g –1 , получаем в левой части полный дифференциал
В результате интегрирования (2.29) приходим к уравнению адиабатного процесса
Графически адиабатный процесс описывается на (р,V) — диаграмме кривыми, похожими на изотермы (рис. 2.12), но идущими круче, так как g > 1, поскольку Сp > СV.
Рис. 2.12. Адиабатный процесс в идеальном газе: 1 — адиабата, 2 — изотерма
Это и понятно, так как при адиабатном расширении газ совершает работу за счет внутренней энергии, и его температура падает, что еще больше уменьшает давление по сравнению с изотермическим расширением.
Экспериментальное исследование адиабатного процесса в идеальном газе можно выполнить с помощью установки, представленной на рис. 2.13.
Рис. 2.13. Экспериментальное изучение адиабатного процесса в идеальном газе
Учитывая, что из уравнения состояния идеального газа следует пропорциональность
уравнение адиабатного процесса можно также представить в виде
Первый закон термодинамики в применении к адиабатному процессу позволяет вычислить работу газа при адиабатном расширении:
Выражения для работы при адиабатном процессе с учетом уравнения Клапейрона — Менделеева можно выразить также через температуры в начале и конце процесса
Для бесконечно малых изменений параметров уравнения (2.32), (2.33) переходят в соотношения
Пример. Горючая смесь в двигателе Дизеля (см. рисунок выше) воспламеняется при температуре Т2 = 1 100 К. Начальная температура смеси Т1 = 350 К. Определим, во сколько раз нужно уменьшить объем смеси при сжатии, чтобы она воспламенилась. Сжатие будем считать адиабатным. Показатель адиабаты для смеси g = 1,4.
Для решения удобнее воспользоваться уравнением адиабатного процесса в форме (2.31):
Отсюда сразу следует выражение для степени сжатия горючей смеси:
Адиабатический процесс
Вы будете перенаправлены на Автор24
Что такое адиабатический процесс
Адиабатическим или адиабатным процессом называют процесс, при котором отсутствует теплообмен с окружающей средой ($delta Q=0$).
В таком случае первое начало термодинамики можно записать в виде:
[0=frac<2>nu RdT+pdV left(1right).]
Из уравнения (1) следует, что при увеличении объема в адиабатном процессе уменьшается температура системы. Или говорят, что в адиабатном процессе работа совершается за счет уменьшения внутренней энергии системы. И обратное справедливо: работа, совершенная над системой, увеличивает внутреннюю энергию системы и, как следствие, температуру. Уравнение, которое характеризует адиабатный процесс в термодинамических параметрах (уравнение адиабаты) носит имя Пуассона. Получим это уравнение для идеального газа. Из уравнения состояния идеального газа:
Из соотношения Майера:
[C_p-C_V=nu R left(3right).]
Подставим (3) в (2), получим:
Разделим уравнение (1) $C_VT ( C_V=frac<2>нR)$, получим:
где $gamma =frac$ — показатель адиабаты. Проинтегрируем уравнение (5):
где $lnA$- некоторая постоянная.
Потенцируем уравнение (6), получаем:
Уравнение (7) есть уравнение адиабаты в параметрах T,V. Для того, чтобы перейти к уравнению адиабаты, в параметрах p,V используют уравнение Менделеева — Клайперона. И получают уравнение адиабаты в виде:
Или в параметрах p,T уравнение (7,8) имеет вид:
Зная, что теплоемкости можно представить как:
показатель адиабаты исходя из ($gamma =frac$) и уравнений (10)
Легко получить формулу работы для адиабатного процесса. По определению работа газа A равна:
где $p_1V_1=nu RT_1.$ Используя уравнение адиабаты, записанное для двух состояний в параметрах $V,T$, получаем:
Что такое адиабата
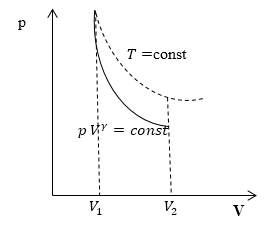
Линия, изображающая на термодинамической диаграмме адиабатный процесс, называется адиабатой (рис.1).
Для сравнения на рис. 1 представлена также изотерма (пунктиром). На рис. 1 видно, что адиабата идет круче, чем изотерма. Работа в адиабатическом процессе по расширению от объема $V_1 $до $V_2$ меньше, чем в изотермическом процессе с таким же изменением объема. Это объясняется тем, что при адиабатном процессе происходит охлаждение газа. В изотермическом процессе при расширении давление уменьшается только за счет уменьшения плотности, тогда как в адиабатном за счет плотности и средней кинетической энергии молекул (соответственно температуры).
Задание: Одноатомный газ совершает адиабатное расширение от объема $V_1=$1$м^3 $при температуре $Т_1=400 К$, при этом давление газа изменяется от $p_1=5cdot <10>^6Па $до $p_2=2cdot <10>^6 Па$. Найдите объем газа в конечном состоянии.
При адиабатном расширении имеем:
где $gamma =frac , $так как газ одноатомный, то i=3, следовательно, $gamma =frac<3+2><3>=frac<5><3>$. Значит можно выразить интересующий нас объем:
Ответ: Объем газа в конечном состоянии 4,6 $м^3.$
Задание: Некоторую массу газа сжали так, что $frac=5$, в первом случае процесс проводился адиабатический, второй изотермический. Начальные состояния газов одинаковы в том и другом случае. Найти отношение работ $frac=?$
Работа в адиабатном процессе задана формулой над газом:
Формула для работы в изотермическом процессе имеет вид:
Тогда найдем искомое отношение:
Для коэффициента адиабаты мы знаем формулу вычисления через число степеней свободы$(i)$, а для одноатомного газа $i=3$:
Подставим данные из условий задачи, получим:
Ответ: Отношение работ, которые совершают над газом в процессах сжатия в адиабатном процессе и изотермическом равно 1,89. Работа над газом в адиабатном процессе больше.
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 26 11 2021
http://online.mephi.ru/courses/physics/molecular_physics/data/course/2/2.4.1.html
http://spravochnick.ru/fizika/termodinamika/adiabaticheskiy_process/
Задача №4. Работа на сжатие пружины
Считая деформации упругими определить работу, которую необходимо совершить, чтобы сжать пружину на 0.3 метра. Жесткость пружины 2,94×103 Н/м.
Дано: x1=0 м; x2=0.3 м; k=2,94×103 Н/м
Найти: A-?
Решение:
Определяем работу по сжатию пружины по формуле


Ответ: работа, необходимая для того, чтобы сжать пружину на 30 сантиметров, равна 132.3 Дж