Как найти работу совершаемую магнитным полем - AvtoShod.ru

На движущиеся
заряды в магнитном поле действует сила
Лоренца, которая всегда перпендикулярна
скорости движения заряженной частицы
и, следовательно, ее перемещению.
Поэтому,

На проводник с
током в магнитном поле действует сила
Ампера. Совершает ли работу эта сила?
Рассмотрим прямолинейный проводник
длиной

и током I
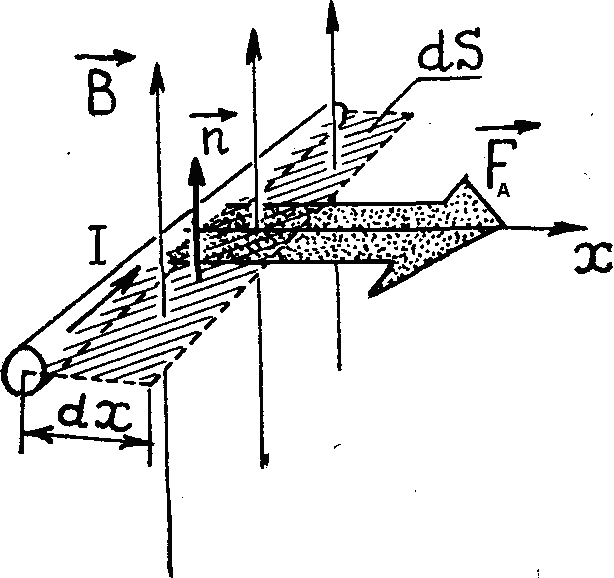
в однородном магнитном поле (рис. 3.22а).
Работа силы Ампера при перемещении
проводника на расстояние
вдоль
направления силы

где
— площадь, которую очерчивает проводник
при движении, ВdS=dФ
— магнитный поток пронизывающий эту
площадь.

dА=IdФ,
(3.32)

а)
б)

Рис.3.22

Следовательно,
элементарная работа, совершаемая силой
Ампера, равна произведению тока в
проводнике I
на магнитный поток dФ,
пронизывающий площадь, которую очерчивает
проводник при своем движении.
При перемещении проводника на конечное
расстояние x,
получаем:
и

(3.33)

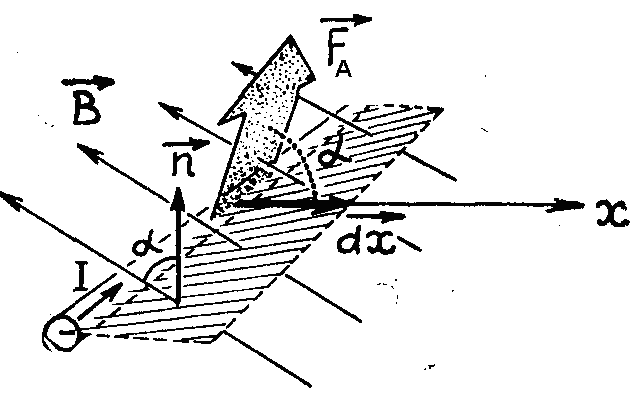
Если
перемещение проводника происходит в
произвольном направлении (рис. 3.22б), то

где
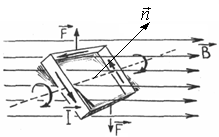
— угол междуиили, что то жеРис.
3.23.

самое,
между
и,
так как,
а.
Ноldх=dS,
BdSсоs=dФ,
так что по-прежнему dA=IdФ.

На
контур с током в магнитном поле действует
сила Ампера
,
которая вращает его вокруг оси (рис.
3.23). Чтобы найти работу, совершаемую
при конечном вращением контура,
необходимо проинтегрировать соотношение
(3.32).

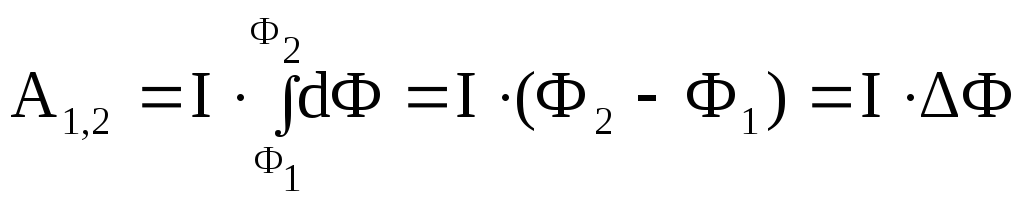
где
ипотоки, пронизывающие контур в его
начальном и конечном положении.

Вопросы и задания
для самопроверки.

Дайте определение
магнитного потока и назовите случаи
когда он максимальный и минимальный.
Чему равен поток
в однородном и неоднородном магнитных
полях?
Чему равен поток
через замкнутую и незамкнутую
поверхности?
В каких единицах
в системе СИ измеряется магнитный
поток?
Выведите формулу
для работы сил по перемещению проводника
в магнитном поле.
Какая сила
совершает работу в магнитном поле?
Будет ли совершаться
работа при движении заряженной частицы
в магнитном поле?

3.16. Магнитное поле в веществе

Вещество состоит
из атомов, а атомы из электронов и ядер.
Электрон, вращаясь по замкнутой орбите
вокруг ядра, образует орбитальный
(дипольный) магнитный момент
.
Кроме того, электрон обладает собственным
механическим моментом,
называемымспином.
Спину
электрона соответствует спиновой
магнитный момент
.
Магнитный момент атома
геометрически складывается из орбитальных
магнитных моментов его электронов,
гдечисло
электронов в атоме.

Внешнее магнитное
поле с индукцией
влияет на магнитные моменты атомов
вещества и создает в нем дополнительное
магнитное поле. Это явление называется
намагничиванием. Индукция магнитного
поля в веществе

,
(3.34)

где
—
индукция магнитного поля, образованного
в результатенамагничивания.

Отличие магнитного
поля в веществе
от индукции внешнего магнитного поляопределяется относительной магнитной
проницаемостью среды.Магнитная
проницаемость показывает, во сколько
раз изменяется магнитное поле в веществе
по сравнению с внешним магнитным полем.
Величина
находится из соотношения

Намагничивание
вещества определяется вектором
намагниченности
:

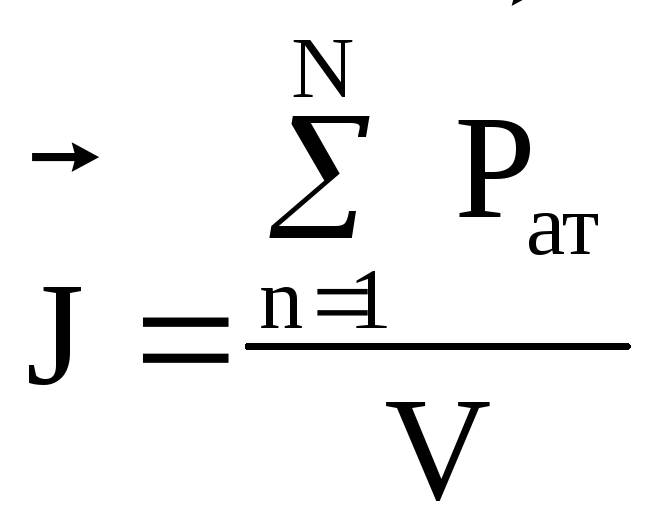
где
— суммарный магнитный моментN
атомов в веществе объёмом V.

Как показывает
опыт, для большинства веществ и слабых
полей, магнитное поле
пропорционально вектору намагниченности
и определяется как

Учитывая, что
равенство (3.34) можно записать в виде:

,
(3.35)

а вектор
намагниченности

(3.36)

где

— магнитная восприимчивость вещества.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
#
#
#
17.05.20158.11 Mб14курс лекций новый.doc
#
#
#
#
#
#
#

Источник

Как и любая другая сила, сила Ампера имеет возможность совершить работу. По определению механической работы:

displaystyle A=FDelta rcos alpha (1)

где

Рис. 1. Работа силы Ампера

Пусть в нашей системе проводник длиной , находящийся в однородном магнитном поле индукции , по которому течёт ток , движется под действием силы Ампера и перемещается на расстояние $displaystyle {{F}_{A}}=IBl$ (рис. 1). Тогда, при условии, что сила Ампера равна $displaystyle {{F}_{A}}=IBl$ , получим:

displaystyle A=IBlDelta rcos alpha (2)

Пометим displaystyle S=lDelta r — площадь, «заметаемая» при движении проводника. Т.е. площадь, которую «прошёл» проводник во время движения. Тогда, в общем случае:

displaystyle A=IBScos alpha (3)

где

Соотношение (3) указывает на работу сил Ампера. Однако, если использовать определение изменения потока магнитного поля:

Ф displaystyle =BDelta Scos alpha (4)

получим:

displaystyle A=IDelta Ф (5)

где

Источник

Работа по перемещению проводника и контура с током в магнитном поле.

На проводник с током в магнитном поле действуют силы, которые определяются с помощью закона Ампера. Если проводник не закреплен (например, одна из сторон контура сделана в виде подвижной перемычки, рис. 1), то под действием силы Ампера он в магнитном поле будет перемещаться. Значит, магнитное поле совершает работу по перемещению проводника с током.

Для вычисления этой работы рассмотрим проводник длиной l с током I (он может свободно двигаться), который помещен в однородное внешнее магнитное поле, которое перпендикулярно плоскости контура. Сила, направление которой определяется по правилу левой руки, а значение — по закону Ампера, рассчитывается по формуле

Под действием данной силы проводник передвинется параллельно самому себе на отрезок dx из положения 1 в положение 2. Работа, которая совершается магнитным полем, равна

так как ldx=dS — площадь, которую пересекает проводник при его перемещении в магнитном поле, BdS=dФ — поток вектора магнитной индукции, который пронизывает эту площадь. Значит,

(1)

т. е. работа по перемещению проводника с током в магнитном поле равна произведению силы тока на магнитный поток, пересеченный движущимся проводником. Данная формула справедлива и для произвольного направления вектора В.

Рассчитаем работу по перемещению замкнутого контура с постоянным током I в магнитном поле. Будем считать, что контур М перемещается в плоскости чертежа и в результате бесконечно малого перемещения перейдет в положение М’, изображенное на рис. 2 штриховой линией. Направление тока в контуре (по часовой стрелке) и магнитного поля (перпендикулярно плоскости чертежа — за чертеж или от нас) дано на рисунке. Контур М условно разобьем на два соединенных своими концами проводника: AВС и CDА.

Работа dA, которая совершается силами Ампера при иссследуемом перемещении контура в магнитном поле, равна алгебраической сумме работ по перемещению проводников AВС (dA1) и CDA (dA2), т. е.

(2)

Силы, которые приложенны к участку CDA контура, образуют острые углы с направлением перемещения, поэтому совершаемая ими работа dA2>0. .Используя (1), находим, эта работа равна произведению силы тока I в нашем контуре на пересеченный проводником CDA магнитный поток. Проводник CDA пересекает при своем движении поток dФ0 сквозь поверхность, выполненную в цвете, и поток dФ2, который пронизывает контур в его конечном положении. Значит,

(3)

Силы, которые действуют на участок AВС контура, образуют тупые углы с направлением перемещения, значит совершаемая ими работа dA1<0. Проводник AВС пересекает при своем движении поток dФ0 сквозь поверхность, выполненную в цвете, и поток dФ1, который пронизывает контур в начальном положении. Значит,

(4)

Подставляя (3) и (4) в (2), найдем выражение для элементарной работы:

где dФ2—dФ1=dФ’ — изменение магнитного потока сквозь площадь, которая ограничена контуром с током. Таким образом,

(5)

Проинтегрировав выражение (5), найдем работу, которая совершается силами Ампера, при конечном произвольном перемещении контура в магнитном поле:

(6)

значит, работа по перемещению замкнутого контура с током в магнитном поле равна произведению силы тока в контуре на изменение магнитного потока, сцепленного с контуром. Выражение (6) верно для контура любой формы в произвольном магнитном поле.

Источник

3.16. Магнитное поле в веществе

Не пропустите также: