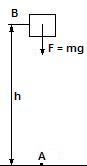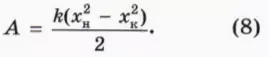Как найти работу силы тяжести в физике

Понятие механической работы

В статье мы расскажем о главных энергетических характеристиках движения: работе и мощности. Дадим этим физическим величинам определение и рассмотрим их основные свойства.

В общем случае под работой в физике понимают меру воздействия силы. Затронем самые простые её разновидности, те, что объясняются законами классической механики.

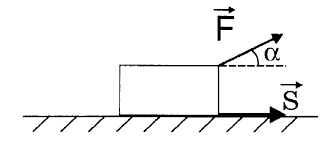
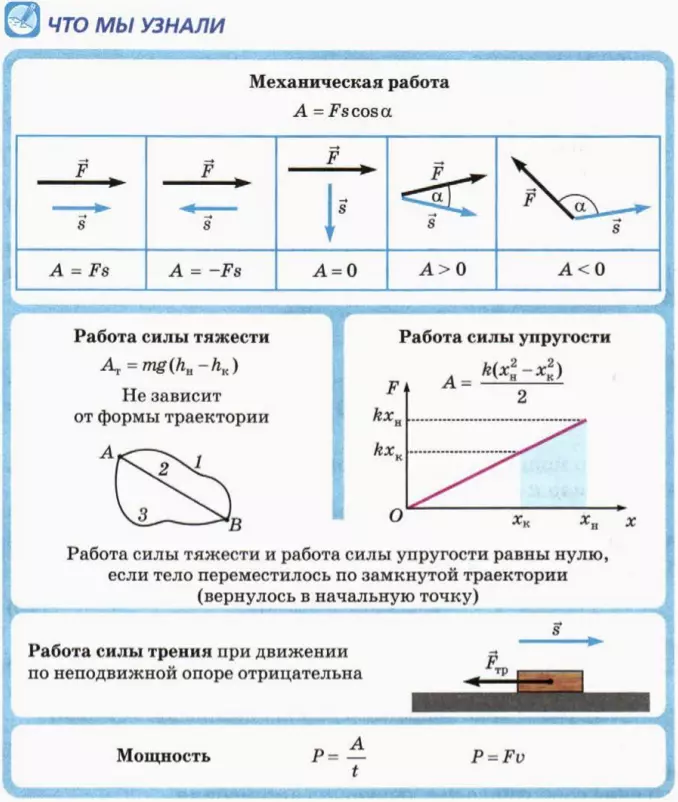
Механическая работа: основные формулы

Работа, совершаемая внешней силой против деформации тела, может быть записана в виде формулы:

A = k*(x₂ – x₁)²/2, где k – коэффициент упругости тела. x₁ и x₂ – начальное и конечное удлинение тела. Получается, что работа в этом случае зависит лишь от координат.

Работа силы тяжести записывается по формуле:

A = m*g*(h₂ – h₁), где m – масса тела. g – ускорение свободного падения. h₁ и h₂ – начальная и конечная высота тела. От траектории тела работа сил тяжести (если считать поле тяготения постоянным и однородным) не зависит.

Работа сил трения записывается по формуле:

A = -F_тр* S, где F_тр – сила трения. S – путь пройденный телом. Обратите внимание, сила взята со знаком минус. Силы трения всегда противоположны перемещению, куда бы тело не двигалось.

В международной системе СИ единицей измерения механической работы считается Джоуль. Он равен работе совершённой силой в 1 Н при перемещении тела в направлении её действия на 1 м.

Результирующая работа сил

Результирующая механическая работа нескольких сил равна сумме работ каждой из них.

[mathrm{A}=sum Delta A i=sum F Delta S i]

Если считать перемещения предельно малыми (ΔS_i→0), то можно перейти к интегралу [mathrm{A}=int_{b}^{a} F(x) d x].

Графически работа изображается как площадь фигуры на графике показывающем зависимость силы от координаты.

Случаи, когда механическая работа не совершается

Рассмотрим их:

• Сила действует, но тело своего местоположения не меняет и не деформируется. Например, когда мы пытаемся сдвинуть с места большой, тяжёлый шкаф;
• Тело движется, но на него не действуют никакие силы либо их действие скомпенсировано. Например, когда тело движется в безвоздушном пространстве только по инерции;
• Сила и перемещение перпендикулярны друг другу. Например, когда на тело действует центростремительная сила.

Из выше сказанного следует, что для совершения работы обязательно наличие действующей на тело силы и перемещение его под действием этой силы.

Мощность: определение, формулы

По виду это выражение очень сильно напоминает формулу выражения скорости, только там вместо работы стоит перемещение. Это не просто совпадение. Мощность действительно можно охарактеризовать, как скорость совершения работы.

Вот ещё несколько формул для выражения мощности:

N = F*S/ Δt = F* v = F* v cos α

v – вектор скорости, v – абсолютная величина скорости, α – угол между скоростью тела и линией действия на него силы.

Из приведённой выше первой формулы для мощности вытекает единица её измерения. Если работа измеряется в джоулях, а время в секундах, то логично предположить, что в системе СИ мощность будет мериться в Джоулях на секунду Дж/с. Так и есть. Единица измерения мощности называется Ватт. 1 Ватт равен работе в 1 Джоуль, которая совершается за 1 секунду. Однако подобная мощность столь мала, что на практике чаще всего используют единицу измерения в тысячу Ватт. Называют её Киловатт (кВт).

На практике мощность нередко указывают в лошадиных силах. Это внесистемная един6ица измерения мощности. 1 лошадиная сила равна 0,735 киловатт или 745.7 Вт. Это так называемая электрическая лошадиная сила, традиционно используется именно в России. Есть ещё механическая лошадиная сила, метрическая лошадиная сила, гидравлическая лошадиная сила и т. д. Все они несколько отличаются от заявленной выше величины.

С
ила
тяжести-сила
действующая на тела вследствие его
притяжения к планете

Сила тяжести,
действующая на тело, является суммой сил,
действующей на
его отдельные части. Если
считать силу тяжести однородной,
то суммарная сила тяжести,
действующая на тело равна произведению
массы всего
тела на ускорение свободного падения.

Работа
силы тяжести равна изменению потенциальной
энергии тела,взятому со знаком минус.

Работу
силы тяжести рассмотрим на примере.
Пусть тело падает под действием силы
тяжести F = mg с высоты h из точки B в точку
A. Формула работы силы:

A
= |F||S|cosα

Подставим
значения для нашего примера:

A
= mgh

косинус
альфа здесь равен единице.

Работа
силы тяжести не зависит от траектории.
То есть, если тело скатывается под
действием силы тяжести с какой-то
наклонной поверхности, то работа силы
тяжести всё равно будет равна mgh.

На
замкнутой траектории работа силы тяжести
равна нулю. Значит сила тяжести является
консервативной силой.

21 Консервативные силы, поле центральных сил

В
физике консервати́вные
си́лы (потенциальные
силы) — силы, работа которых
не зависит от формы траектории (зависит
только от начальной и конечной точки
приложения сил). Отсюда следует следующее
определение: консервативные силы —
такие силы, работа по любой замкнутой
траектории которых
равна 0.Если в системе действуют только
консервативные силы, то механическая
энергия системы сохраняется. Для
консервативных сил выполняются следующие
тождества:

• 
   — ротор консервативных
  сил равен 0;

• 
   — работа консервативных
  сил по произвольному замкнутому контуру
  равна 0;

• 
   —
  консервативная
  сила является градиентом некой скалярной
  функции U,
  называемой силовой. Эта функция
  равна потенциальной
  энергии взятой
  с обратным знаком.

Примерами
консервативных сил являются: сила
тяжести, сила
упругости

Модель
поля центральных сил

поле,
характерной особенностью которого
является то, что силы, действующие на
него при любом его положении в поле,
всегда проходят через некоторую
определенную
точку
называемую центром сил или центром
поля. Поле центральных сил может иметь
различную
физическую
природу, но напряженность его всегда
обратно пропорциональна квадрату
расстояния до
центра поля.

Примерами
центральных сил служат силы тяготения,
направленные к центру Солнца или
планеты,

кулоновские
силы электростатического притяжения
и отталкивания и др.  Рассмотрим
важный случай поля центральных сил.
Всякое силовое поле вызывается действием
определенных тел. Сила, действующая на
частицу А в таком поле, обусловлена
взаимодействием этой частицы с данными
телами. Если силы, зависят только от
расстояния между взаимодействующими
частицами и направлены по прямой,
соединяющей эти частицы, от их
называют центральными. Такими
примерами служат силы гравитационные,
кулоновские и упругие.

     Центральную
силу, действующую на частицу А со
стороны частицы В, можно представить
в общем виде:

     где 
 -функция,
зависящая при данном характере
взаимодействия только от r — расстояния
между частицами; 
 единичный
вектор, задающий направление радиус-вектора
частицы А относительно частицы В
(рис.5.6).

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Совсем недавно, мы
изучили работу силы. Напомним, что работа силы равна произведению модуля силы,
модуля перемещения и косинуса угла между направлениями силы и перемещения:

Рассмотрим теперь частный
случай — работу силы тяжести при перемещении тела с высоты h₁
на высоту h₂.

Первый случай — это
падение тела вертикально вниз.

В этом случае,
перемещение, конечно же, будет равно

Сила тяжести, как мы
знаем, равна

.

Поскольку сила тяжести
направлена вертикально вниз, как и перемещение, косинус угла между
направлениями этих векторов равен единице. Таким образом, мы получим, что
работа силы тяжести равна:

Второй случай — это когда
тело, наоборот, подбрасывают вертикально вверх с высоты h₁
на высоту h₂.

В этом случае, угол между
направлением силы тяжести и направлением перемещения составит 180^о.
Это приводит нас к тому, что работа силы тяжести опять-таки равна:

Наконец, рассмотрим
случай, когда между направлением силы тяжести и перемещением существует
произвольный угол α.

Обозначим модуль
перемещения за s. В этом случае,
работа силы тяжести равна:

Но, исходя из определения
косинуса:

Таким образом, мы в
третий раз получили одинаковый результат.

Более того, если даже мы
рассмотрим криволинейную траекторию, то убедимся, что результат будет тем же.

Любую кривую мы можем
представить в виде ломаной линии, состоящей из очень маленьких горизонтальных и
вертикальных отрезков. На горизонтальных отрезках работа силы тяжести будет
равна нулю, поскольку в этом случае направление перемещения перпендикулярно
направлению силы тяжести. На вертикальных участках работа будет равна: A
= mg(s₁
+ … + s_n).
Очевидно, что эта сумма будет равна (h₁
– h₂):

Таким образом, мы
убедились, что работа силы тяжести не зависит от траектории движения тела.
Имеет значение лишь то, насколько начальное положение тела отличается от
конечного. Это плавно подводит нас к понятию потенциальной энергии, которое
мы рассмотрим немного позже.

Из приведенных примеров
вытекает еще один важный вывод: при движении тела по замкнутой траектории
работа силы тяжести равна нулю. Для начала рассмотрим контур, имеющий форму
прямоугольника. Как мы уже убедились, при движении тела в горизонтальном
направлении, работа силы тяжести равна нулю. Вектор перемещения направлен
перпендикулярно вектору силы тяжести. При перемещении же по противолежащим
вертикальным сторонам контура, сила тяжести совершает работу, равную по
абсолютной величине, но противоположную по знаку.

В одном случае вектор
перемещения направлен так же, как вектор силы тяжести, а в другом — направлен в
противоположную сторону. Это довольно логично, поскольку при движении тела
вниз, сила тяжести ему «помогает», а при движении вверх — наоборот, мешает.

Мы можем сколь угодно
усложнить эту траекторию, получив совершенно произвольный замкнутый контур.

Но опять же, разбив все
кривые на ломаные линии с горизонтальными и вертикальными участками, мы
убедимся, что суммарная работа будет равна нулю.

Силы, обладающие такими
свойствами, называются консервативными. То есть, консервативная сила — это
такая сила, работа которой в замкнутом контуре равна нулю.

Примеры решения задач.

Задача 1. Охотник
стреляет со скалы под углом 40° к горизонту. За время падения пули работа силы
тяжести составила 5 Дж. Если пуля вошла в землю на расстоянии 250 м от скалы,
то какова её масса?

Задача 2. Находясь
на Нептуне, тело совершило перемещение так, как показано на рисунке. При этом
перемещении работа силы тяжести составила 840 Дж. Если масса данного тела равна
5 кг, то каково ускорение свободного падения на Нептуне?

1. Определение работы

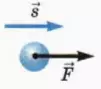
С механической работой (работой силы) вы уже знакомы из курса физики основной школы. Напомним приведенное там определение механической работы для следующих случаев.

Если сила направлена так же, как перемещение тела, то работа силы

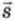
A = Fs     (1)

В этом случае работа силы положительна.

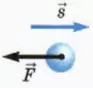
Если сила направлена противоположно перемещению тела, то работа силы

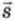
A = –Fs     (2)

В этом случае работа силы отрицательна.

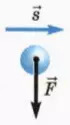
Если сила f_vec направлена перпендикулярно перемещению s_vec тела, то работа силы равна нулю:

A = 0      (3)

Работа – скалярная величина. Единицу работы называют джоуль (обозначают: Дж) в честь английского ученого Джеймса Джоуля, сыгравшего важную роль в открытии закона сохранения энергии. Из формулы (1) следует:

1 Дж = 1 Н * м.

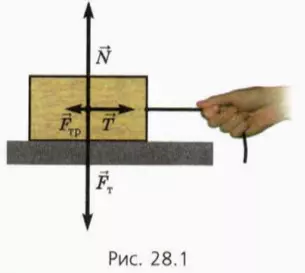
? 1. Брусок массой 0,5 кг переместили по столу на 2 м, прикладывая к нему силу упругости, равную 4 Н (рис. 28.1). Коэффициент трения между бруском и столом равен 0,2. Чему равна работа действующей на брусок:
а) силы тяжести m?
б) силы нормальной реакции ?
в) силы упругости ?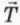
г) силы трения скольжения _тр?

Суммарную работу нескольких сил, действующих на тело, можно найти двумя способами:
1. Найти работу каждой силы и сложить эти работы с учетом знаков.
2. Найти равнодействующую всех приложенных к телу сил и вычислить работу равнодействующей.

Оба способа приводят к одному и тому же результату. Чтобы убедиться в этом, вернитесь к предыдущему заданию и ответьте на вопросы задания 2.

? 2. Чему равна:
а) сумма работ всех действующих на брусок сил?
б) равнодействующая всех действующих на брусок сил?
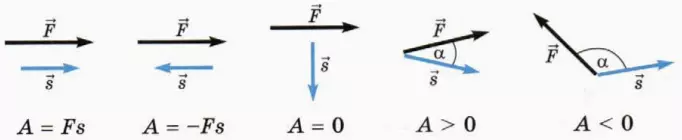
в) работа равнодействующей? В общем случае (когда сила f_vec направлена под произвольным углом к перемещению s_vec) определение работы силы таково.

Работа A постоянной силы равна произведению модуля силы F на модуль перемещения s и на косинус угла α между направлением силы и направлением перемещения:

A = Fs cos α     (4)

? 3. Покажите, что из общего определения работы следуют к выводы, показанные на следующей схеме. Сформулируйте их словесно и запишите в тетрадь.

? 4. К находящемуся на столе бруску приложена сила, модуль которой 10 Н. Чему равен угол между этой силой и перемещением бруска, если при перемещении бруска по столу на 60 см эта сила совершила работу: а) 3 Дж; б) –3 Дж; в) –3 Дж; г) –6 Дж? Сделайте пояснительные чертежи.

2. Работа силы тяжести

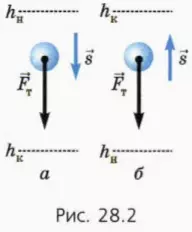
Пусть тело массой m движется вертикально от начальной высоты h_н до конечной высоты h_к.

Если тело движется вниз (h_н > h_к, рис. 28.2, а), направление перемещения совпадает с направлением силы тяжести, поэтому работа силы тяжести положительна. Если же тело движется вверх (h_н < h_к, рис. 28.2, б), то работа силы тяжести отрицательна.

В обоих случаях работа силы тяжести

A = mg(h_н – h_к).     (5)

Найдем теперь работу силы тяжести при движении под углом к вертикали.

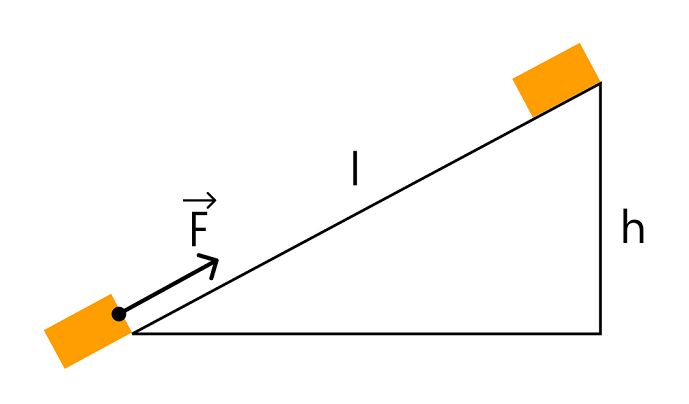
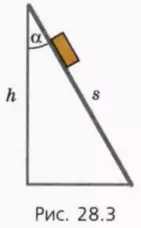
? 5. Небольшой брусок массой m соскользнул вдоль наклонной плоскости длиной s и высотой h (рис. 28.3). Наклонная плоскость составляет угол α с вертикалью.

а) Чему равен угол между направлением силы тяжести и направлением перемещения бруска? Сделайте пояснительный чертеж.
б) Выразите работу силы тяжести через m, g, s, α.
в) Выразите s через h и α.
г) Выразите работу силы тяжести через m, g, h.
д) Чему равна работа силы тяжести при движении бруска вдоль всей этой же плоскости вверх?

Выполнив это задание, вы убедились, что работа силы тяжести выражается формулой (5) и тогда, когда тело движется под углом к вертикали – как вниз, так и вверх.

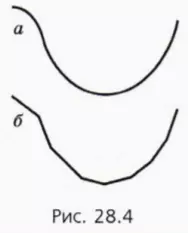
Но тогда формула (5) для работы силы тяжести справедлива при движении тела по любой траектории, потому что любую траекторию (рис. 28.4, а) можно представить как совокупность малых «наклонных плоскостей» (рис. 28.4, б).

Таким образом,
работа силы тяжести при движении но любой траектории выражается формулой

A_т = mg(h_н – h_к),

где h_н – начальная высота тела, h_к – его конечная высота.
Работа силы тяжести не зависит от формы траектории.

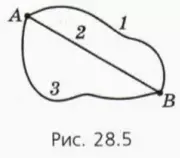
Например, работа силы тяжести при перемещении тела из точки A в точку B (рис. 28.5) по траектории 1, 2 или 3 одинакова. Отсюда, в частности, следует, что рибота силы тяжести при перемещении по замкнутой траектории (когда тело возвращается в исходную точку) равна нулю.

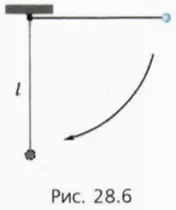
? 6. Шар массой m, висящий на нити длиной l, отклонили на 90º, держа нить натянутой, и отпустили без толчка.
а) Чему равна работа силы тяжести за время, в течение которого шар движется к положению равновесия (рис. 28.6)?
б) Чему равна работа силы упругости нити за то же время?
в) Чему равна работа равнодействующей сил, приложенных к шару, за то же время?

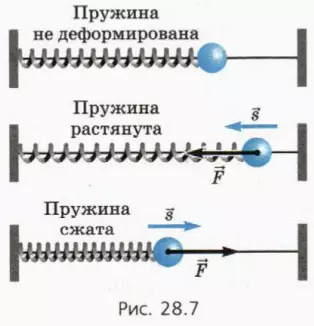
3. Работа силы упругости

Когда пружина возвращается в недеформированное состояние, сила упругости совершает всегда положительную работу: ее направление совпадает с направлением перемещения (рис. 28.7).

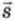
Найдем работу силы упругости .
Модуль этой силы связан с модулем деформации x соотношением (см. § 15)

F = kx.     (6)

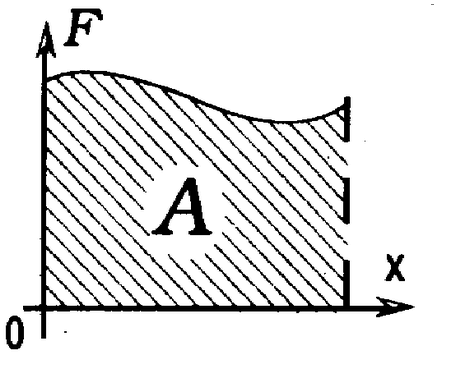
Работу такой силы можно найти графически.

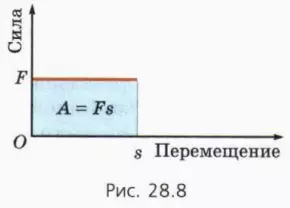
Заметим сначала, что работа постоянной силы численно равна площади прямоугольника под графиком зависимости силы от перемещения (рис. 28.8).

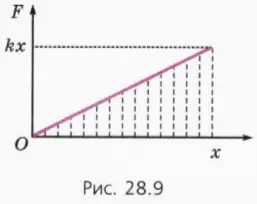
На рисунке 28.9 изображен график зависимости F(x) для силы упругости. Разобьем мысленно все перемещение тела на столь малые промежутки, чтобы на каждом из них силу можно было считать постоянной.

Тогда работа на каждом из этих промежутков численно равна площади фигуры под соответствующим участком графика. Вся же работа равна сумме работ на этих участках.

Следовательно, и в этом случае работа численно равна площади фигуры под графиком зависимости F(x).

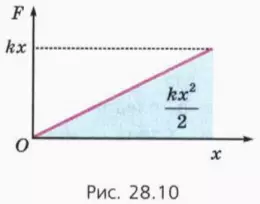
? 7. Используя рисунок 28.10, докажите, что

работа силы упругости при возвращении пружины в недеформированное состояние выражается формулой

A = (kx₂)/2.     (7)

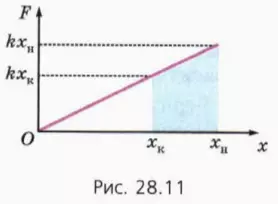
? 8. Используя график на рисунке 28.11, докажите, что при изменении деформации пружины от x_н до x_к работа силы упругости выражается формулой

Из формулы (8) мы видим, что работа силы упругости зависит только от начальной и конечной деформации пружины, Поэтому если тело сначала деформируют, а потом оно возвращается в начальное состояние, то работа силы упругости равна нулю. Напомним, что таким же свойством обладает и работа силы тяжести.

? 9. В начальный момент растяжение пружины жесткостью 400 Н/м равно 3 см. Пружину растянули еще на 2 см.
а) Чему равна конечная деформация пружины?
б) Чему равна работа силы упругости пружины?

? 10. В начальный момент пружина жесткостью 200 Н/м растянута на 2 см, а в конечный момент она сжата на 1 см. Чему равна работа силы упругости пружины?

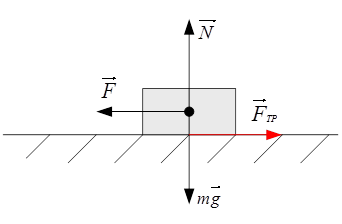
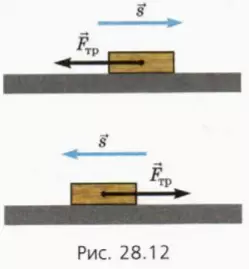
4. Работа силы трения

Пусть тело скользит по неподвижной опоре. Действующая на тело сила трения скольжения направлена всегда противоположно перемещению и, следовательно, работа силы трения скольжения отрицательно при любом направлении перемещения (рис. 28.12).

Поэтому если сдвинуть брусок вправо, а пегом на такое же расстояние влево, то, хотя он и вернется в начальное положение, суммарная работа силы трения скольжения не будет равна нулю. В этом состоит важнейшее отличие работы силы трения скольжения от работы силы тяжести и силы упругости. Напомним, что работа этих сил при перемещении тела по замкнутой траектории равна нулю.

? 11. Брусок массой 1 кг передвигали по столу так, что его траекторией оказался квадрат со стороной 50 см.
а) Вернулся ли брусок в начальную точку?
б) Чему равна суммарная работа действовавшей на брусок силы трения? Коэффициент трения между бруском и столом равен 0,3.

5. Мощность

Часто важна не только совершаемая работа, но и скорость совершения работы. Она характеризуется мощностью.

Мощностью P называют отношение совершенной работы A к промежутку времени t, за который эта работа совершена:

P = A/t.      (9)

(Иногда мощность в механике обозначают буквой N, а в электродинамике – буквой P. Мы считаем более удобным одинаковое обозначение мощности.)

Единица мощности – ватт (обозначают: Вт), названная в честь английского изобретателя Джеймса Уатта. Из формулы (9) следует, что

1 Вт = 1 Дж/c.

? 12. Какую мощность развивает человек, равномерно поднимая ведро воды массой 10 кг на высоту 1 м в течение 2 с?

Часто мощность удобно выражать не через работу и время, а через силу и скорость.

Рассмотрим случай, когда сила направлена вдоль перемещения. Тогда работа силы A = Fs. Подставляя это выражение в формулу (9) для мощности, получаем:

P = (Fs)/t = F(s/t) = Fv.     (10)

? 13. Автомобиль едет по горизонтальной дороге со скоростью 72 км/ч. При этом его двигатель развивает мощность 20 кВт. Чему равна сила сопротивления движению автомобиля?

Подсказка. Когда автомобиль движется по горизонтальной дороге с постоянной скоростью, сила тяги равна по модулю силе сопротивления движению автомобиля.

? 14. Сколько времени потребуется для равномерного подъема бетонного блока массой 4 т на высоту 30 м, если мощность двигателя подъемного крана 20 кВт, а КПД электродвигателя подъемного крана равен 75%?

Подсказка. КПД электродвигателя равен отношению работы по подъему груза к работе двигателя.

Дополнительные вопросы и задания

15. Мяч массой 200 г бросили с балкона высотой 10 и под углом 45º к горизонту. Достигнув в полете максимальной высоты 15 м, мяч упал на землю.
а) Чему равна работа силы тяжести при подъеме мяча?
б) Чему равна работа силы тяжести при спуске мяча?
в) Чему равна работа силы тяжести за все время полета мяча?
г) Есть ли в условии лишние данные?

16. Шар массой 0,5 кг подвешен к пружине жесткостью 250 Н/м и находится в равновесии. Шар поднимают так, чтобы пружина стала недеформированной, и отпускают без толчка.
а) На какую высоту подняли шар?
б) Чему равна работа силы тяжести за время, в течение которого шар движется к положению равновесия?
в) Чему равна работа силы упругости за время, в течение которого шар движется к положению равновесия?
г) Чему равна работа равнодействующей всех приложенных к шару сил за время, в течение которого шар движется к положению равновесия?

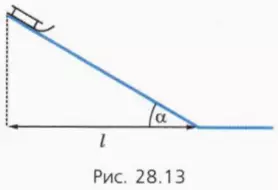
17. Санки массой 10 кг съезжают без начальной скорости со снежной горы с углом наклона α = 30º и проезжают некоторое расстояние по горизонтальной поверхности (рис. 28.13). Коэффициент трения между санками и снегом 0,1. Длина основания горы l = 15 м.

а) Чему равен модуль силы трения при движении санок по горизонтальной поверхности?
б) Чему равна работа силы трения при движении санок по горизонтальной поверхности на пути 20 м?
в) Чему равен модуль силы трения при движении санок по горе?
г) Чему равна работа силы трения при спуске санок?
д) Чему равна работа силы тяжести при спуске санок?
е) Чему равна работа равнодействующей сил, действующих на санки, при их спуске с горы?

18. Автомобиль массой 1 т движется со скоростью 50 км/ч. Двигатель развивает мощность 10 кВт. Расход бензина составляет 8 л на 100 км. Плотность бензина 750 кг/м₃, а его удельная теплота сгорания 45 МДж/кг. Чему равен КПД двигателя? Есть ли в условии лишние данные?
Подсказка. КПД теплового двигателя равен отношению совершенной двигателем работы к количеству теплоты, которое выделилось при сгорании топлива.

Сила, перемещающая тело, совершает работу. Работа – это разность энергии тела в начале процесса и в его конце. А мощность – это работа за одну секунду. Коэффициент полезного действия (КПД) – это дробное число. Максимальный КПД равен единице, однако, часто, КПД меньше единицы.

Работы силы, формула

Сила, приложенная к телу и перемещающая его, совершает работу (рис. 1).

Работа силы — это скалярное произведение вектора силы на вектор перемещения.

Работу, совершаемую силой, можно посчитать, используя векторный или скалярный вид записи такой формулы:

Векторный вид записи

[ large boxed{ A = left( vec{F} , vec{S} right) }]

Для решения задач правую часть этой формулы удобно записывать в скалярном виде:

[ large boxed{ A = left| vec{F} right| cdot left| vec{S} right| cdot cos(alpha) }]

( F left( H right) ) – сила, перемещающая тело;

( S left( text{м} right) ) – перемещение тела под действием силы;

( alpha ) – угол между вектором силы и вектором перемещения тела;

Работу обозначают символом (A) и измеряют в Джоулях. Работа – это скалярная величина.

В случае, когда сила постоянная, формула позволяет рассчитать работу, совершенную силой за полное время ее действия.

Если сила изменяется со временем, то в каждый конкретный момент времени будем получать мгновенную работу. Эти, мгновенные значения для разных моментов времени будут различаться.

Рассмотрим несколько случаев, следующих из формулы:

1. Когда угол между силой и перемещением острый, работа силы положительная;
2. А если угол тупой — работа отрицательная, так как косинус тупого угла отрицательный;
3. Если же угол прямой – работа равна нулю. Сила, перпендикулярная перемещению, работу не совершает!

Работа — разность кинетической энергии

Работу можно рассчитать еще одним способом — измеряя кинетическую энергию тела в начале и в конце процесса движения. Рассмотрим такой пример. Пусть автомобиль, движется по горизонтальной прямой и, при этом увеличивает свою скорость (рис. 2). Масса автомобиля 1000 кг. В начале его скорость равнялась 1 м/с. После разгона скорость автомобиля равна 10 метрам в секунду. Найдем работу, которую пришлось проделать, чтобы ускорить этот автомобиль.

Для этого посчитаем энергию движения автомобиля в начале и в конце разгона.

( E_{k1} left(text{Дж} right) )  – начальная кинетическая энергия машины;

( E_{k2} left(text{Дж} right) )  – конечная кинетическая энергия машины;

( m left( text{кг}right) ) – масса автомобиля;

( displaystyle v left( frac{text{м}}{c}right) ) – скорость, с которой машина движется.

Кинетическую энергию будем вычислять, используя формулу:

[ large E_{k} = m cdot frac{v^{2}}{2} ]

[ large E_{k1} = 1000 cdot frac{1^{2}}{2} = 500 left(text{Дж} right) ]

[ large E_{k2} = 1000 cdot frac{10^{2}}{2} = 50000 left(text{Дж} right) ]

Теперь найдем разницу кинетической энергии в конце и вначале разгона.

[ large boxed{ A = Delta E_{k} }]

[ large Delta E_{k} = E_{k2} — E_{k1} ]

[ large Delta E_{k} = 50000 – 500 = 49500 left(text{Дж} right) ]

Значит, работа, которую потребовалось совершить, чтобы разогнать машину массой 1000 кг от скорости 1 м/с до скорости 10 м/с, равняется 49500 Джоулям.

Примечание: Работа – это разность энергии в конце процесса и в его начале. Можно находить разность кинетической энергии, а можно — разность энергии потенциальной.

[ large boxed{ A = Delta E }]

Работа силы тяжести — разность потенциальной энергии

Рассмотрим теперь следующий пример. Яблоко массой 0,2 кг упало на садовый стол с ветки, находящейся на высоте 3 метра от поверхности земли. Столешница располагается на высоте 1 метр от поверхности (рис. 3). Найдем работу силы тяжести в этом процессе.

Посчитаем потенциальную энергию яблока до его падения и энергию яблока на столешнице.

( E_{p1} left(text{Дж} right) )  – начальная потенциальная энергия яблока;

( E_{p2} left(text{Дж} right) )  – конечная потенциальная энергия яблока;

Примечание: Работу можно рассчитать через разность потенциальной энергии тела.

Потенциальную энергию будем вычислять, используя формулу:

[ large E_{p} = m cdot g cdot  h]

( m left( text{кг}right) ) – масса яблока;

Величина ( displaystyle g approx 10 left(frac{text{м}}{c^{2}} right) ) – ускорение свободного падения.

( h left( text{м}right) ) – высота, на которой находится яблоко относительно поверхности земли.

Начальная высота яблока над поверхностью земли равна 3 метрам

[ large E_{p2} = 0,2 cdot 10 cdot  3 = 6 left(text{Дж} right) ]

Потенциальная энергия яблока на столе

[ large E_{p1} = 0,2 cdot 10 cdot  1 = 2 left(text{Дж} right) ]

Теперь найдем разницу потенциальной энергии яблока в конце падения и перед его началом.

[ large Delta E_{p} = E_{p2} — E_{p1} ]

[ large Delta E_{p} = 2 – 6 = — 4 left(text{Дж} right) ]

Важно помнить: Когда тело падает на землю, его потенциальная энергия уменьшается. Сила тяжести при этом совершает положительную работу!

Чтобы работа получилась положительной, в правой части формулы перед ( Delta  E_{p}) дополнительно допишем знак «минус».

[ large boxed{ A = — Delta E_{p} }]

Значит, работа, которую потребовалось совершить силе тяжести, чтобы яблоко массой 0,2 кг упало с высоты 3 м на высоту 1 метр, равняется 4 Джоулям.

Примечания:

1. Если тело падает на землю, работа силы тяжести положительна;
2. Когда мы поднимаем тело над землей, мы совершаем работу против силы тяжести. Наша работа при этом положительна, а работа силы тяжести будет отрицательной;
3. Сила тяжести относится к консервативным силам. Для консервативных сил перед разностью потенциальной энергии мы дописываем знак «минус»;
4. Работа силы тяжести не зависит от траектории, по которой двигалось тело;
5. Работа для силы (displaystyle F_{text{тяж}}) зависит только от разности высот, в которых тело находилось в конечный и начальный моменты времени.

Рисунок 4 иллюстрирует факт, что для силы (displaystyle F_{text{тяж}}) работа зависит только от разности высот и не зависит от траектории, по которой тело двигалось.

Мощность

В механике мощность часто обозначают символами N или P и измеряют в Ваттах в честь шотландского изобретателя Джеймса Уатта.

Примечание: Символ (vec{N}) используется для обозначения силы реакции опоры — она измеряется в Ньютонах и является векторной величиной. Чтобы не возникло путаницы, мощность вместо N будем обозначать символом P. Символ P – первая буква в английском слове power – мощность.

Мощность – это работа, совершенная за одну секунду (энергия, затраченная за 1 сек).

Расчет работы осуществляем, используя любую из формул:

[ large A = Delta E_{k} ]

[ large A = Delta E_{p} ]

[ large A = F cdot S cdot cos(alpha) ]

Разделив эту работу на время, в течение которого она совершалась, получим мощность.

[ large boxed{ P = frac{A}{Delta t} }]

Если работа совершалась равными частями за одинаковые интервалы времени – мощность будет постоянной величиной.

Мощность переменная, когда в некоторые интервалы времени совершалось больше работы.

Еще одна формула для расчета мощности

Есть еще один способ расчета мощности, когда сила перемещает тело и при этом скорость тела не меняется:

[ large P = left( vec{F} , vec{v} right) ]

Формулу можно записать в скалярном виде:

[ large P = left| vec{F} right| cdot left| vec{v} right| cdot cos(alpha) ]

( F left( H right) ) – сила, перемещающая тело;

( displaystyle v left( frac{text{м}}{c} right) ) – скорость тела;

( alpha ) – угол между вектором силы и вектором скорости тела;

Когда векторы (vec{F}) и (vec{v}) параллельны, запись формулы упрощается:

[ large boxed{ P = F cdot v }]

Примечание: Такую формулу для расчета мощности можно получить из выражения для работы силы, разделив обе части этого выражения на время, в течение которого работа совершалась (а если точнее, найдя производную обеих частей уравнения).

КПД

КПД – коэффициент полезного действия. Обычно обозначают греческим символом (eta) «эта». Единиц измерения не имеет, выражается либо десятичной дробью, либо в процентах.

Примечания:

1. Процент – это дробь, у которой в знаменателе число 100.
2. КПД — это либо правильная дробь, или дробь, равная единице.

Вычисляют коэффициент (eta) для какого-либо устройства, механизма или процесса.

[ large boxed{ eta = frac{ A_{text{полезная}}}{ A_{text{вся}}} }]

(eta) – КПД;

( large A_{text{полезная}} left(text{Дж} right)) – полезная работа;

(large A_{text{вся}} left(text{Дж} right)) – вся затраченная для выполнения работы энергия;

Примечание: КПД часто меньше единицы, так как всегда есть потери энергии. Коэффициент полезного действия не может быть больше единицы, так как это противоречит закону сохранения энергии.

[ large boxed{ eta leq 1 }]

Величина (eta) является дробной величиной. Если числитель и знаменатель дроби разделить на одно и то же число, полученная дробь будет равна исходной. Используя этот факт, можно вычислять КПД, используя мощности:

[ large boxed{ eta = frac{ P_{text{полезная}}}{ P_{text{вся затраченная}}} }]

Выводы

1. Сила, приложенная к телу и перемещающая его, совершает работу;
2. Когда угол между силой и перемещением острый, работа силы положительная, а если угол тупой — работа отрицательная; Если же угол прямой – работа равна нулю. Сила, перпендикулярная перемещению, работу не совершает!
3. Работу можно вычислить, измеряя кинетическую энергию тела в начале и в конце его движения;
4. Вычислить работу можно через разность потенциальной энергии тела в начальной и в конечной высотах над землей;
5. Когда тело падает на землю, его потенциальная энергия уменьшается. Сила тяжести при этом совершает положительную работу!
6. Мы совершаем работу против силы тяжести, когда поднимаем тело над землей. При этом наша работа положительная, а работа силы тяжести — отрицательная;
7. Сила тяжести — это консервативная сила. Поэтому, работа силы (displaystyle F_{text{тяж}}) не зависит от траектории, по которой двигалось тело, а зависит только от разности высот, в которых тело находилось в конечный и начальный моменты времени;
8. Мощность – это работа, совершенная за одну секунду, или затраченная за 1 сек. энергия;
9. Коэффициент полезного действия обозначают греческим символом (eta) «эта», единиц измерения не имеет, выражается либо десятичной дробью, либо в процентах;
10. КПД — это либо правильная дробь, или дробь, равная единице.
11. Можно вычислять КПД, подставляя в формулу работу, или мощности