МИНЕСТЕРСТВО
ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное
государственное бюджетное образовательное
учреждение
Высшего
профессионального образования
НАЦИОНАЛЬНЫЙ
ИСЛЕДОВАТЕЛЬСКИЙ
ТОМСКИЙ
ПОЛИТЕХНИЧЕКИЙ УНИВЕРСИТЕТ
Институт
— Неразрушающего контроля
Направление
— Электроника и наноэлектроника;
Биотехнические системы и технологии
Кафедра
— Промышленной и медицинской электроники
ОПРЕДЕЛЕНИЕ
СРЕДНЕЙ СИЛЫ СОПРОТИВЛЕНИЯ
ГРУНТА
ЗАБИВКЕ СВАИ
Отчёт
по лабораторной работе № 1-10
По
курсу «Физика 1.3»
Выполнил
студент гр.ЭТО133 ________ ________ Е.И.Зубова
________
________ А.С.Молдабеков
Проверил
ассистент каф. ОФ ________ ________ Л.А.Святкин
ОПРЕДЕЛЕНИЕ
СРЕДНЕЙ СИЛЫ СОПРОТИВЛЕНИЯ
ГРУНТА
ЗАБИВКЕ СВАИ
Цель
работы:
определение средней силы сопротивления
грунта забивке сваи, оценка потери
механической энергии при забивке сваи.
Приборы
и принадлежности:
модель копра, штангенциркуль, линейка.
ТЕОРИТИЧЕСКАЯ
ЧАСТЬ
Процесс
забивки сваи в грунт с помощью копра
происходит следующим образом. При
падении груза его
потенциальная
энергия,
обусловленная взаимодействием с
Землей, переходит в кинетическую энергию
движения груза (приращением кинетической
энергии Земли при этом можно пренебречь).
Обозначив через v1
скорость груза непосредственно перед
соударением со сваей, через m1
– массу груза и через Н
– первоначальную высоту груза над
сваей, получим уравнения:

(1)
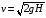
(2)
При
дальнейшем движении груза происходит
его неупругое соударение со сваей.
Физические явления во время столкновения
довольно сложны. Сталкивающиеся тела
деформируются, возникают упругие силы
и силы трения, в телах возбуждаются
колебания и волны и т.д. Однако если
удар неупругий, в конечном итоге,
все эти процессы прекращаются и в
дальнейшем груз и свая, соединившись
вместе, движутся как единое целое с
массой (m1
+ m2)
c
некоторой общей скоростью v,
сохраняя возникшую при ударе взаимную
деформацию. Общую скорость груза и сваи
сразу после удара можно найти, применяя
закон сохранения импульса к системе
«груз–свая». Эту систему на рассматриваемом
этапе взаимодействия считаем замкнутой,
так как внешние силы – силы тяжести
груза и сваи, сила сопротивления грунта
малы по сравнению с внутренними силами,
развивающимися при соударении между
грузом и сваей. До удара груз двигался
со скоростью v1,
приобретенной в результате падения с
высоты Н,
свая же была неподвижна. После удара
груз и свая движутся с общей скоростью
v.
Согласно
закону сохранения импульса, считая
удар груза и сваи абсолютно неупругим,
запишем:
m1v1
= (m1
+ m2)v.
Подставляя
сюда (2), имеем

(3)
В
дальнейшем система «груз–свая»,
перемещаясь внутри грунта с начальной
скоростью v,
испытывает действие силы сопротивления
со стороны грунта. Грунт может иметь
различную плотность на различных
глубинах, поэтому и сила сопротивления
будет разной. Поэтому в дальнейшем
будем говорить о средней
силе
сопротивления
грунта забивке сваи (Fср).
По
окончании удара груз и свая движутся
вместе замедленно до полной остановки.
При этом сила сопротивления грунта
совершает работу, равную

(4)
где
S
– смещение сваи с грузом в грунте.
Так
как сила сопротивления грунта Fср
и смещение направлены по одной прямой,
но в противоположные стороны, то cos
= 1.
Тогда
А
= Fср
S
.
(5)
Эта
работа равна изменению энергии системы
«груз–свая–Земля», т.е.
FсрS
= W2
– W1
или
FсрS
= W1
W2,
(6)
где
W1
и W2
– механическая энергия системы в начале
движения и в момент остановки,
соответственно.
Обозначим
высоту забиваемой сваи относительно
заранее выбранного начального уровня
перед началом забивки сваи h1
и после окончания забивки h2
(см. рис. 2). Тогда

(7)

(8)
а
разность

(9)
Обозначим
h1
– h2
= S.
(10)
Подставив
в (6) (W1
– W2)
из (9), v
из (3), S
из (10), имеем
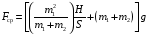
(11)
Примечание:
при неупругом ударе происходят различного
рода процессы в соударяющихся телах
(их пластические деформации, трение и
др.). В результате происходит частичное
преобразование механической энергии
во внутреннюю энергию соударяющихся
тел.
Проведем
оценку потери кинетической энергии
системы «груз–свая» в результате
неупругого удара. Кинетическая энергия
системы до удара

Кинетическая энергия системы после
удара

Потери
кинетической энергии во время удара
W
= W0
– W
=
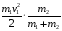
Относительное
уменьшение кинетической энергии системы
Практическая
часть
Таблица№1
Зависимость смещения сваи от высоты
падения груза
|
h1, |
L, |
H, |
h2, |
hср, |
S,м |
Fcр,H |
|
0.06 |
0.2 |
0.31 |
0.052 0.053 0.051 0.050 0.052 |
0.052 |
0.008 |
114 |
|
0.28 |
0.053 0.054 0.053 0.052 0.055 |
0.053 |
0.007 |
117,8 |
||
|
0.25 |
0.053 0.054 0.055 0.056 |
0.054 |
0.006 |
122,2 |
||
|
0.22 |
0.054 0.054 0.057 0.056 |
0.055 |
0.005 |
128,9 |
||
|
0.19 |
0.055 0.054 0.056 0.058 0.057 |
0.056 |
0.004 |
135,2 |
m1=330гр=0.33кг;
m2=45гр=0.045кг
-
hcp1=
=0.052м
hcp4==0.055м
hcp2==0.053м
hcp5==0.056м
hcp3==0.054м
-
S1=h1-hcp1=0.008м
S4=h4-hcp4=0.005м
S2=h2-hcp2=0.007м
S5=h5-hcp5=0.004м
S3=h3-hcp3=0.006м -
Fcp1=
≈114H
Fcp2=≈117,8H
Fcp3=≈122,2H
Fcp4=≈128,9H
Fcp5=≈135,2H
Таблица
№2 Зависимость
силы от удаленности гири на рычаге
|
h1, |
Н, |
L, |
h2, |
hср, |
S,м |
Fcр,H |
|
0.06 |
0.31 |
0.1 |
0.051 0.052 0.049 0.050 |
0.05 |
0.01 |
91,9 |
|
0.13 |
0.052 0.053 0.050 0.054 |
0.051 |
0.009 |
101,7 |
||
|
0.16 |
0.054 0.053 0.052 0.055 |
0.053 |
0.007 |
129,7 |
||
|
0.19 |
0.054 0.056 0.053 0.054 |
0.054 |
0.006 |
150,7 |
||
|
0.22 |
0.056 0.053 0.054 0.055 |
0.055 |
0.005 |
180,1 |
m1=330гр=0.33кг;
m2=45гр=0.045кг
-
hcp1=
=0.05м
hcp2==0.051м
hcp3==0.053м
hcp4==0.054м
hcp5==0.055м
-
S1=h1-hcp1=0.01м
S2=h2-hcp2=0.009м
S3=h3-hcp3=0.007м
S4=h4-hcp4=0.006м
S5=h5-hcp5=0.005м
-
Fcp1=
≈91,9H
Fcp2=≈101,7H
Fcp3=≈129,7Н
Fcp4=≈150,7H
Fcp5=≈180,1H
Вычислим
абсолютную погрешность измерений ∆H
и ∆Fcp
для последнего измерения:
∆H=∆Hои=α∙0.5∙lmin=0.000475м
∆S=
0.0005 м
∆Fcp=
ϭF=(∆Fcp/Fcp)∙100%=6,5%
(для второго измерения)
График
1. Зависимость смещения от начальной
высоты груз
а
График
2. Зависимость силы сопротивления
начальной высоты груза
График
3. Зависимость силы от расстояния L
При
максимальной начальной высоте груза:
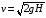

W
=
≈0.077Дж
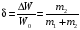
Вывод:
В
ходе эксперимента были найдены значения
средней силы сопротивления груза при
различных значениях начальной высоты
сваи и установлена линейная зависимость.
Также были найдены значения средней
силы сопротивления при переменной
удаленности груза на рычаге и установлена
линейная зависимость и были вычислены
погрешности (∆H
и ∆Fcp).
В модели Копра используют понятие
средней силы сопротивления, так как на
различный глубинах плотность грунта
неодинакова. Так же было определено
относительное уменьшение кинетической
энергии системы δ=14%
Томск
20113
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Условие задачи:
Тело массой 2 кг падает с высоты 10 м и углубляется в песок на глубину 0,5 м. Определить среднюю силу сопротивления песка.
Задача №2.8.6 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
(m=2) кг, (H=10) м, (h=0,5) м, (F-?)
Решение задачи:
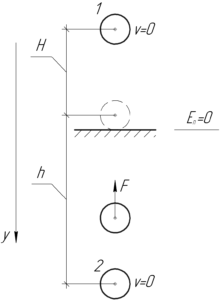
Сила сопротивления песка – это неконсервативная сила. Согласно закону сохранения энергии работа неконсервативной силы есть изменение полной механической энергии:
[A = {E_2} – {E_1}]
Работа силы сопротивления песка (F) отрицательна, так как вектор силы и вектор перемещения направлены в разные стороны. Она равна:
[A = – F cdot h]
В точке 1 и 2 у тела имеется только потенциальная энергия, равная соответственно в каждой точке:
[{E_1} = mgH]
[{E_2} = – mgh]
Потенциальная энергия в точке 2 отрицательна, так как эта точка находится ниже принятого нуля потенциальной энергии. В точках 1 и 2 кинетической энергии у тела нет.
В итоге:
[ – F cdot h = – mgh – mgH]
[F cdot h = mgh + mgH]
[F = frac{{mgleft( {h + H} right)}}{h}]
Посчитаем ответ:
[F = frac{{2 cdot 10 cdot left( {0,5 + 10} right)}}{{0,5}} = 420; Н = 0,42; кН]
Ответ: 0,42 кН.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.8.5 Какую скорость приобретает ракета массой 2 кг, если продукты горения массой
2.8.7 Брусок массой 1 кг первоначально покоился на вершине наклонной плоскости
2.8.8 Велосипедист движется со скоростью 8 м/с. Определить расстояние, пройденное
Мощность, затрачиваемая на работу ротора и откосников, складывается из следующей суммы:
, (3.10)
где — мощность, затрачиваемая на копание грунта ковшами; — мощность, затрачиваемая на резание грунта откосниками; — мощность, затрачиваемая на подъем грунта ковшами.
Мощность, потребляемая при копании грунта ковшами, определяется по формуле (II.59) стр. 186 [1].
, (3.11)
где k — удельное сопротивление копанию, кгс/см2, по табл. 10 (стр. 186 [1]) для III категории грунта принимаем k = 7,5.
Следовательно:
л.с.
Мощность, потребляемая при резании грунта откосниками, определяется по формуле (II.60) стр. 187 [1].
, (3.12)
где — площадь сечения траншеи, разрабатываемая откосниками, м2, по техническим характеристикам экскаватора (см. раздел 2.2) определяем = 0,7 м2; — удельное сопротивление разработке грунта откосниками, кгс/см2, определяется по формуле (II.61, стр. 187 [1]) .
Следовательно:
л.с.
Мощность, необходима для подъема грунта ковшами определяется по формуле (II.62) стр. 187 [1].
, (3.13)
где — удельный вес грунта, тс/м3, принимаем = 2,5; Н — глубина траншеи, м; Н0 — расстояние от поверхности земли до точки выгрузки грунта (до середины ковша, находящего в верхнем положении), м, принимаем Н0 = 4,4 м.
Следовательно:
л.с.
Следовательно, мощность, затрачиваемая на работу ротора и откосников:
л.с.
Мощность, потребляемая транспортером — при ориентировочном расчете воспользуемся формулой (II.75) стр. 193 [1].
л.с. (3.14)
Мощность двигателя, необходима для рабочего передвижения экскаватора — при ориентировочном расчете воспользуемся формулой (II.68) стр. 190 [1].
л.с. (3.15)
Определение сил сопротивления копанию
При работе экскаватора на его ковш действует сила сопротивления грунта копанию, которую можно разложить на касательную Рк и нормальную РN составляющие (см. чертеж №2, положение I).
Толщина стружки, срезаемой ковшом, величина переменная, изменяющаяся от минимального значения, соответствующего началу копания, до максимального, равного подаче на ковш, соответствующего моменту выхода ковша из забоя.
Поскольку одновременно в забое находятся несколько ковше, каждый из них в одно и то же время срезает стружку разной толщины. Поэтому ковши испытывают со стороны грунта различные сопротивления копанию. Максимальная сила сопротивления действует на верхний ковш перед моментом его выхода из забоя, а точнее, когда его режущий инструмент находится в диаметральной горизонтальной плоскости ротора.
Среднее суммарное окружное усилие копания Рокр на роторе равно сумме касательных сил Ркi сопротивления грунта копанию на ковшах:
, (3.16)
где Ркi — усилие копания на отдельном ковше; n — скорость вращения ротора, об/мин; D — диаметр ротора по кромкам зубьев, м.
Следовательно:
кгс.
15.2.10. Вывести расчетную формулу для коэффициента Пуассона.
15.2.11. Какая величина измеряется в данной работе? Как она связана с молекулярными теплоемкостями газа и
?
ОТВЕТЫ НА ВОПРОСЫ ПО ЗАЩИТЕ ЛАБОРАТОРНЫХ РАБОТ ПО ФИЗИКЕ.
Лабораторная работа № 6. (Изучение средней силы сопротивления грунта и изучение неупругого соударения груза и сваи на модели копра.)
6.1.1. II Закон Ньютона: «Ускорение материальной точки пропорционально вызывающей его силе, совпадает с ней по направлению и обратно пропорционально массе материальной точки».
Согласно современной терминологии: «Скорость изменения импульса материальной точки равна действующей на нее силе».
6.1.2. Закон сохранения импульса системы тел: «Импульс замкнутой системы не изменяется с течением времени».
и
6.1.3. Закон сохранения механической энергии: «Механическая энергия консервативной системы не изменяется с течением времени».
(Система консервативна, если все действующие на нее внешние и внутренние непотенциальные силы не совершают работы ( ), а все внешние потенциальные силы стационарны).
6.1.4. Сила F, действующая на материальную точку М называется потенциальной (консервативной), если работа этой силы зависит только от начального и конечного положений точки М. (Пример: гравитационные силы и силы упругости)
Диссипативными называются силы, зависящие от скоростей точек механической системы и совершающие отрицательную суммарную работу при любых перемещениях этой системы.
(Пример: силы трения скольжения, силы сопротивления движению).
-
Замкнутая система- механическая система, на которую не действуют внешние силы.
Строго говоря, замкнутых систем нет, так как на все тела действуют действуют внешние силы. Приблизительно замкнутой можно считать Солнечную систему, так как внешние силы тяготения, действующие на тела солнечной системы пренебрежительно малы по сравнению с силами тяготения этих сил друг к другу.
6.2.1. Суммарный импульс системы взаимодействующих тел груз-свая сохраняется, так как сумма внешних сил, действующих на каждое тело системы, много меньше сил взаимодействия между телами, возникающих при ударе. Действием внешних сил за время удара на рассматриваемую систему тел можно пренебречь. Данная система считается приближенно замкнутой.
Выведение формулы (4) описания.
При падении груза с высоты Н молная механическая энергия системы груз-земля сохраняется и поэтому можно записать:
,
(где — масса груза,
— скорость груза перед ударом).
Отсюда следует, что:
.
Так как систему можно считать условно замкнутой, то выполняется закон сохранения импульса:
,
(где — масса сваи,
— общая скорость сваи и груза после удара).
Получаем:
6.2.2. Да изменяется. На этапе после неупругого удара груза и сваи, когда груз и свая начинают двигаться замедленно до полной остановки. На этом этапе сила сопротивления грунта, являющаяся диссипативной совершает работу. Полная механическая энергия системы груз-свая-земля не сохраняется.
6.2.3. Сила сопротивления грунта зависит от высоты H, с которой сбрасывается груз. (А меняя деформацию пружины мы меняем силу нормального давления со стороны пружины на втулку, играющую роль грунта.)
Выведение формулы (10) описания.
(где и
— соответственно изменения кинетической и потенциальной энергиисваи и груза от начала их совместного движения до остановки).
,
(где — перемещение груза и сваи от начала их движения до остановки).
На участке средняя сила сопротивления грунта
совершает работу
(где угол , так как направления силы и перемещения взаимно противоположны)
Следовательно
.
Получаем
=
Разделив левую и правую части уравнения на и подставив значение
Получим:

6.2.4. Из формулы (9) описания выражаем :

6.2.5. = -0.41x 9.8 x 0.23 x
6.2.6. 
6.3.1. . Серия опытов делается потому, что существует погрешность измерения по линейке. Инструментальная погрешность этого измерения равна инструментальной погрешности измерения по линейке и равна 5 мм. Она зависит от неточности изготовления прибора, неточности нашего считывания.
6.3.2. Сила сопростивления грунта определяется массой груза, массой сваи, высотой, с которой сбросили груз.
6.3.3. .
Лабораторная работа № 7. (Изучение динамики вращательного движения твердого тела и определение момента инерции маятника Обербека.)
7.1.1. Основное уравнение динамики вращательного движения: . (
) , где Oz- ось вращения.
7.1.2. Основное уравнение динамики вращательного движения твердого тела: .
7.1.3. Момент инерции является мерой инертности тела во вращательном движении (аналог массы в поступательном движении). Он зависит как от массы тела, так и от ее распределения по объему тела. Кроме того момент инерции зависит от выбора оси вращения. Момент инерции твердого тела равен сумме моментов инерции его частей. В частности, если тело разбить на элементарные массы , то по определению
, (где
— расстояние от элементарной массы
до оси вращения).
7.1.4. Моментом силы относительно неподвижной оси а называется скалярная величина равная проекции на эту ось вектора момента силы относительно какой-нибудь точки, лежащей на оси а или векторная величина
, где
— орт оси а.
Также , (где
— расстояние от точки приложения силы до оси, а
— проекция силы F на направление вектора
=v/
, где v-линейная скорость этой точки вращающегося тела.
7.1.5. Кинематической характеристикой направления и быстроты вращения тела служит угловая скорость тела, равная отношению вектора элементарного поворота тела к продолжительности этого поворота: .
Частота вращения показывает сколько оборотов совершает за единицу времени тело, равномерно вращающееся с угловой скоростью .
.
Линейная скорость точки тела: .
Период вращения: промежуток времени , в течение которого тело, равномерно вращаясь с угловой скоростью
совершает один оборот.
Угловое ускорение: вектор, характеризущий быстроту изменения угловой скорости тела:
.
Вращательное ускорение: .
7.1.6. Состоянием механического равновесия называется такое состояние системы, из которого она может быть выведена только в результате внешнего силового воздействия.
Состояние механического равновесия называется устойчивым, если малое внешнее воздействие на систему вызывает малое изменение ее состояния.
Состояние механического равновесия называется неустойчивым, если система при сколь угодно малом внешнем воздействии выходит из этого состояния и не возвращается в него.
7.2.1. РИСУНОК В ЛАБОРАТОРНОЙ РАБОТЕ.
7.2.2. Это сила натяжения нити Т.
7.2.3. , где
-момент инерции маятника,
— угловое ускорение,
— радиус шкива, на который наматывается нить.
7.2.4. ;
;
;
;
;
7.2.5. Увеличивая радиус, мы увеличиваем момент инерции, а следовательно время уменьшается.
7.3.1. Маятник Обербека— тело сложной геометрической формы (крестообразной). Он состоит из двух шкивов различного радиуса, укрепленных на одной горизонтальной оси, четырех стержней с грузиками одинаковой массы.
7.3.2. Потому что после удара о пол линейное ускорение становится равным нулю. Точность этих измерений равна точности измерений секундомера и равна 0.01 секунды.
7.3.3. Изменить вращающий момент можно, изменяя радиус шкива или массу груза.
изменяя радиус шкива или массу груза.
7.3.4. Изменять момент сил, а следовательно и момент инерции, можно, меняя распределение массы маятника, то есть приближая или отдаляя 4 грузика к (или от) оси вращения.
Момент инерции максимален при наиболее далеком положении грузиков от оси вращения.
7.3.5. Положения безразличного равновесия добиваются проверкой равновесия в двух взаимно перпендикулярных положениях крестовины: сначала один из стержней располагают горизонтально, потом другой- маятник не должен вращаться.
Да, результаты увеличатся.
7.3.6. 

7.5.1. Скамья Жуковского представляет собой горизонтальную платформу, свободно вращающуюся вокруг вертикальной оси. Момент инерции уменьшается, а угловая скорость возрастает при сведении рук человека к груди.
Лабораторная работа № 8. (Изучение динамики плоского движения Маятника Максвелла.)
8.1.1. Движение называется плоским или плоскопараллельным, если при этом движении все точки тела движутся в параллельных плоскостях. (Качение однородного кругового цилиндра по плоскости.
8.1.2. Момент инерции зависит от выбора оси вращения. Момент инерции твердого тела равен сумме моментов инерции его частей. В частности, если тело разбить на элементарные массы , то по определению
, (где
— расстояние от элементарной массы
до оси вращения).
8.1.3. Центр масс тела- точка С, радиус-вектор которой равен отношению суммы произведений масс всех материальных точек системы на их радиусы-векторы к массе всей системы:
,
(где и
— масса и радиус вектор i-й материальной точки, n и m=
— общее число этих точек в системе и ее суммарная масса).
Центр масс тела- геометрическая точка, для которой сума произведений масс всех материальных точек, образующих механическую систему, на их радиусы-векторы, проведенные из этой точки, равна нулю.
8.1.4. Теорема Кёнига: «Кинетическая энергия механической системы равна сумме кинетической энергии той же системы в ее движении относительно системы центра масс и кинетической энергии, которую имела бы рассматриваемая система, двигаясь поступательно со скоростью центра масс» :
Кинетическая энергия твердого тела при плоском движении равна:



 =0.052м
=0.052м =0.055м
=0.055м =0.053м
=0.053м =0.056м
=0.056м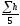 =0.054м
=0.054м ≈114H
≈114H ≈117,8H
≈117,8H ≈122,2H
≈122,2H ≈128,9H
≈128,9H ≈135,2H
≈135,2H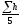 =0.05м
=0.05м =0.051м
=0.051м =0.053м
=0.053м =0.054м
=0.054м =0.055м
=0.055м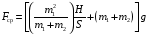 ≈91,9H
≈91,9H ≈101,7H
≈101,7H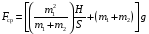 ≈129,7Н
≈129,7Н ≈150,7H
≈150,7H ≈180,1H
≈180,1H











